基于直观想象的深度解题探究

摘 要：文章通过对一道三棱锥的外接球问题进行多维度、多角度探析，还原数学本质，精选教学素材的同时，实现一题多解到多题一解的能力转变，从而培养学生解题思维、提升直观想象力。

关键词：三棱锥的外接球；直观想象；深度解题

中图分类号：G633.6 文献标识码：A 文章编号：1673-8918（2024）28-0073-04

《普通高中数学课程标准（2017年版）》指出：直观想象是指借助几何直观和空间想象感知事物的形态与变化，利用图形理解和解决数学问题的过程，主要包括：借助空间认识事物的位置关系、形态变化与运动规律；利用图形描述、分析数学问题；建立数与形的联系，构建数学问题直观模型，探索解决问题的思路。在立体几何的日常教学中，教师通过引导学生多画图、多观察几类特殊几何体的特征，让学生研究几何体的几何特征并展开联想，通过旋转、补形等方式深度感悟，提升直观想象力。

一、 试题呈现

在一次联考中，有这样一道试题：

在三棱锥A-BCD中，AB=CD=4，CA=BD=2，BC=23，二面角A-BC-D的平面角为60°，则它的外接球的表面积为 。

经考后分析，此题得分率不高，究其原因是本题没有给出图形，学生自己画出来的图形不准确，缺乏直观想象，很难找出外接球的球心。

二、 解法探究

思路1：大多数学生选择用建系的方法，通过设点的方式，把球心坐标计算出来，但计算量很大、费时费力。

解法1：以B为坐标原点，建立如图1所示的空间直角坐标系，

则C（23，0，0），D（0，2，0），设A为（a，b，c），

由题意知，AC⊥BC，BC⊥BD，

故CA与BD的夹角等于二面角A-BC-D的平面角，

则cos60°=CA·BD｜CA｜·｜BD｜，得12=2b2·2，

由｜BA｜2=a2+b2+c2=16｜CA｜2=（a-23）2+b2+c2=4，解得a=23，b=1，c=3，点A为（23，1，3），

设球心O为（x，y，z），则R2=｜OB｜2=｜OA｜2=｜OC｜2=｜OD｜2得，

R2=x2+y2+z2=（x-23）2+（y-1）2+（z-3）2=（x-23）2+y2+z2=x2+（y-2）2+z2

解得，x=3，y=1，c=33，则R2=｜OB｜2=133，故外接球表面积为4πR2=52π3。

思路2：从补形的角度观察几何体的特征。

可以看出上述解法计算量大，费时费力，教师从点A的坐标出发，引导学生观察点A在底面BCD的投影在过C点且平行于BD的直线上，因此可以将三棱锥补形为棱柱。

解法2：如图2所示，观察三棱柱ACE-BDF，由二面角A-BC-D的平面角为60°可知△ACE为等边三角形，故三棱柱ACE-BDF为正三棱柱。

易知三棱锥的外接球就是三棱柱的外接球，如图3所示，球心在O1O2的中点，半径OA=AO22+O2O2=43+3=133，故外接球表面积为4πR2=52π3。

思路3：从翻折的角度观察几何体的特征。

从题意可知，本题的三棱锥A-BCD是由两个Rt△ABC，Rt△BCD沿着BC边翻折而成，如图4所示。

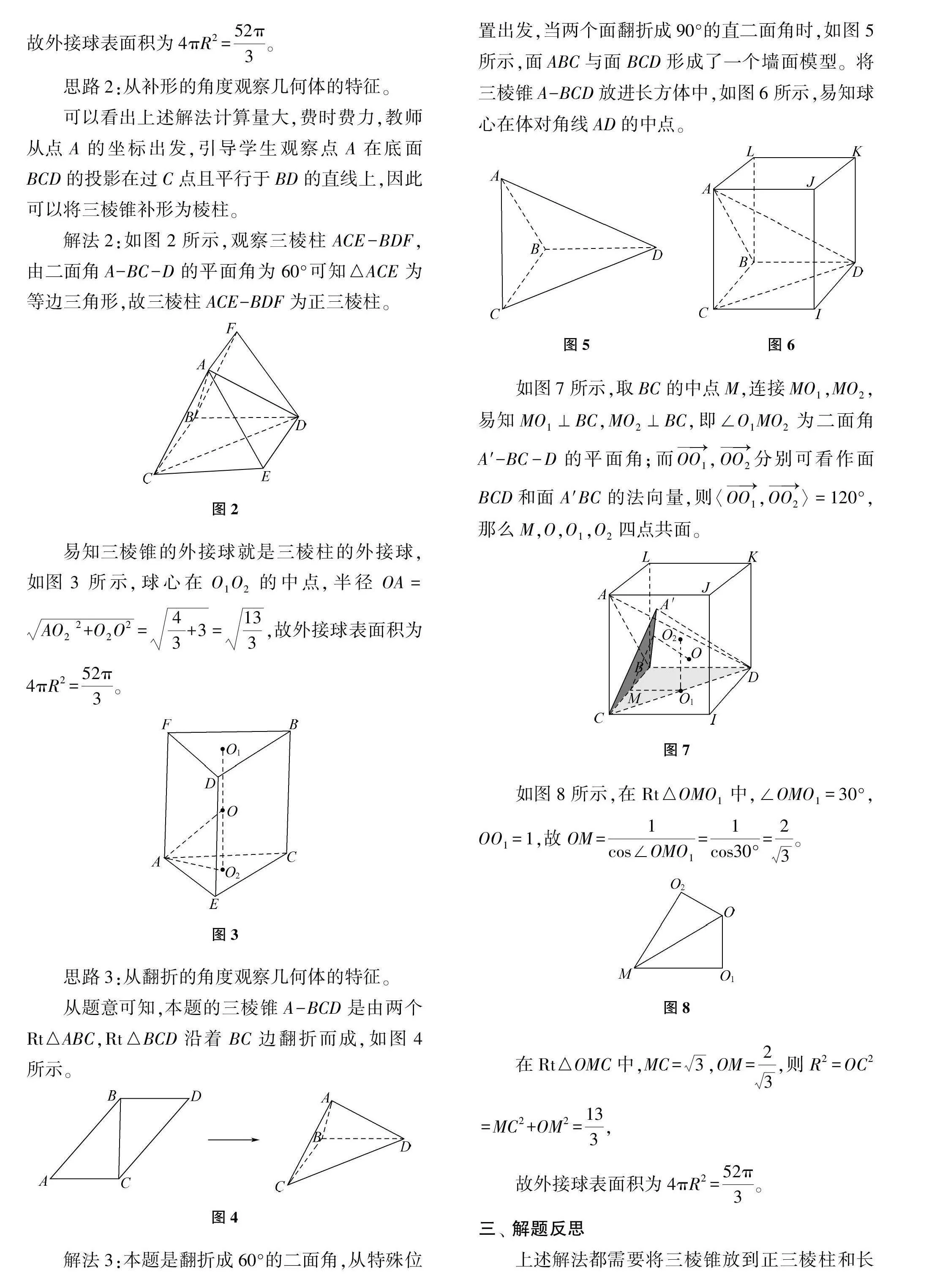
解法3：本题是翻折成60°的二面角，从特殊位置出发，当两个面翻折成90°的直二面角时，如图5所示，面ABC与面BCD形成了一个墙面模型。将三棱锥A-BCD放进长方体中，如图6所示，易知球心在体对角线AD的中点。

如图7所示，取BC的中点M，连接MO1，MO2，易知MO1⊥BC，MO2⊥BC，即∠O1MO2为二面角A′-BC-D的平面角；而OO1，OO2分别可看作面BCD和面A′BC的法向量，则〈OO1，OO2〉=120°，那么M，O，O1，O2四点共面。

如图8所示，在Rt△OMO1中，∠OMO1=30°，OO1=1，故OM=1cos∠OMO1=1cos30°=23。

在Rt△OMC中，MC=3，OM=23，则R2=OC2=MC2+OM2=133，

故外接球表面积为4πR2=52π3。

三、 解题反思

上述解法都需要将三棱锥放到正三棱柱和长方体模型中来解题的，对于不能放进几何模型的题型该如何解决呢？

下面探究解决这类问题的通法通解：

如图9所示，在球O中任取两个相交的截面圆，记两个交点分别为A，B，两个截面圆的圆心分别为O1，O2，取AB的中点M，连接O1M和O2M。

由圆的垂径定理知，O1M⊥AB，O2M⊥AB，

故∠O2MO1为两个截面圆所成二面角的平面角，

易知OO1⊥圆面O1，OO2⊥圆面O2，∠O1OO2+∠O1MO2=π，故O，O1，O2，M四点共圆。

在四边形OO1MO2中，∠OO1M=∠OO2M=π2，

即OM为O，O1，O2，M四点所在外接圆O3的直径，记为2r，外接球的半径为R，则R2=OA2=AB22+（2r）2。

即外接球球心由两个截面圆过圆心的面的垂线的确定。

对本题而言，容易得到△ABC和△BCD为直角三角形，则这两个三角形的外接圆的圆心均在斜边的中点O2和O1，如图10所示，

∵MO2=12AB=1，MO1=12BD=1，∠O1MO2=60°，则O1O2=1，

在△O1O2M中，由正弦定理得，2r=O1O2sin60°=23，

∴R2=OC2=AB22+（2r）2=（3）2+232=133，

故外接球表面积为4πR2=52π3。

四、 变式拓展

变式1：在四面体S-ABC中，AB⊥BC，AB=BC=2，SA=SC=2，SB=6，则此四面体的外接球表面积为 。

由题意可知，△ABC为直角三角形，则其外接圆的圆心在AC的中点D，△SAC为等边三角形，则其外接圆的圆心在中线SD的三等分点O1处。如图11所示，过D，O1分别向各自所在的平面作垂线，则球心为交点O。易知SD=3，DB=1，O1D=33，因为SB=6。在△SDB中，由余弦定理得，SB2=SD2+DB2-2DB·SD×cos∠SDB，解得cos∠SDB=-33。

因为sin∠SDO=sin∠SDB-π2=-cos∠SDB=33，所以OO1=OD1×tan∠ODO1=33×22=66。

设外接球半径为R，则R2=SO21+OO21=32，故外接球表面积为4πR2=6π。

变式2：在四面体S-ABC中，SA⊥面ABC，∠BAC=120°，SA=AC=2，AB=1，则它的外接球的表面积为 。

解：易知SB和SC分别为Rt△ABS和Rt△ACS的斜边，如图12所示，分别取中点O2，O1，过O1，O2分别向各自所在的平面作垂线，则球心为交点O。如图13所示，在四边形OO1O2M中，∵MO2=12AB=12，MO1=12AC=1，∠O1MO2=∠BAC=120°，由余弦定理得，O1O22=14+1-2×12×1cos120°=74，即O1O2=72。

在△O1O2M中，由正弦定理得，2r=O1O2sin120°=73，

∴R2=OC2=AS22+（2r）2=12+732=103，故外接球表面积为4πR2=40π3。

另解：如图14所示，分别找△ABC和△SAC的外接圆的圆心O2，O1，分别取中点O2，O1，过O1，O2分别向各自所在的平面作垂线，则球心为交点O。

在△ABC中，AB=1，AC=2，∠BAC=120°，由余弦定理得，BC2=1+2-2×1×2cos120°=7，即BC=7。

设△ABC的外接圆的半径为r，由正弦定理得，2r=BCsin120°=273，则r=AO2=73，而OO2=12SA=1，故R2=OA2=（OO2）2+（AO2）2=12+732=103，

故外接球表面积为4πR2=40π3。

从本题的两种解法看出，不管找几何体哪个面所在的截面圆，都可以很快找到外接球球心；然后通过解三角形相关知识，求出外接球的半径。其计算难度比建系设点以及套用模型的方法难度小，做到了从一题多解到多题一解的思维转变。

五、 结论

通过以上例子可以看出，立体几何问题在求解的过程中，教师要引导学生准确地画出几何图形，感受图形的几何特征，提高直观想象核心素养和空间想象能力。在实际求解过程中，教师要引导学生可以将空间问题平面化，将三维空间问题转化为二维平面问题来解决，实现降维的目的，降低思维难度。

参考文献：

［1］中华人民共和国教育部.普通高中数学课程标准（2017年版）［S］.北京：人民教育出版社，2018.

［2］罗增儒.数学解题学引论［M］.西安：陕西师范大学出版总社，2016.