间隔织物双剑杆织机平行打纬机构箱体的振动分析

摘" " 要： 针对双剑杆织机共轭凸轮与四连杆组合的平行打纬机构箱体随着织机转速的提高产生强烈振动，影响打纬精度和可靠性的问题，采用理论分析与虚拟仿真结合的方法对打纬机构及箱体进行动应力和振动特性研究。建立了平行打纬机构的动态静力分析方程，运用ADAMS软件对机构进行多体动力学仿真，求解箱体所受的支反力；构建箱体—弹簧阻尼—柔性基础的系统模型，分析箱体在竖直方向的受迫振动，并在仿真过程中探索减小箱体振动的方法。研究结果表明：摆臂轴孔处箱体所受支反力峰值最大，打纬推程阶段箱体的受力最为集中；当凸轮轴转速为260 r/min时齿轮啮合频率与箱体一阶固有频率相等，会产生共振，应避免使用这一转速工作；箱体在竖直方向上产生周期性振动，增加螺栓个数和附加动力减震器有助于改善箱体的振动特性，振幅分别减少38%和23%。

关键词： 双剑杆织机； 平行打纬机构； 支反力； 动态静力分析； 弹簧阻尼； 减振

中图分类号： TS103.135" " " " " "文献标志码： A" " " " " " " " 文章编号： １６７１－０２４Ｘ（２０24）０3－００82－07

Vibration analysis of parallel beating up mechanism box of

double rapier loom for spacer fabric

YANG Jiancheng1，2，3， LIU Yanzhe1，2，3， HUANG Ziwen1，2，3， ZHAO Quanpeng1，2，3， LIU Jian1，2，3

（1. School of Mechanical Engineering， Tiangong University， Tianjin 300387， China； 2. Tianjin Key Laboratory of Advanced Mechatronics Equipment Technology， Tiangong University， Tianjin 300387， China； 3. Tianjin Virtual Simulation Experi-mental Teaching Center of Mechanical Fundamentals and Textile Equipment Design， Tiangong University， Tianjin 300387， China）

Abstract： Aiming at the problem that the parallel beating up mechanism box of double rapier loom with conjugate cam and four-bar linkage generates strong vibration with the increase of loom speed， which destroys the accuracy and reliability of beating up， the dynamic stress and vibration characteristics of the beating up mechanism and box are studied by combining theoretical analysis with virtual simulation. The dynamic static analysis equation of parallel beating up mechanism is established， and the multi-body dynamics simulation of the mechanism is carried out using ADAMS software to solve the reaction force on the box. The system model of box-spring damping-flexible foundation is built， the forced vibration of box in vertical direction is analyzed， and the method to reduce the vibration of box is explored in the simulation process. The results show that the peak value of the reaction force on the box body at the shaft hole of the swing arm is the largest， and the force on the box body is the most concentrated during the beating up and pushing process. When the cam shaft rotates at 260 r/min， the gear meshing frequency is equal to the first order natural frequency of the box， which will produce resonance. The speed should be avoided during operation. The box produces periodic vibration in the vertical direction. Increasing the number of bolts and adding dynamic shock absorbers will help to improve the vibration characteristics of the box， the amplitude decrease by 38% and 23%， respectively.

Key words： double rapier loom； parallel beating up mechanism； support reaction force； dynamic static analysis； spring damping； damping

共轭凸轮与四连杆组合的平行打纬机构主要应用于高速大间隔织物双剑杆织机，这一打纬机构有效解决了织造间隔织物时要求每层纬纱所受打纬力应均匀的问题。目前装备共轭凸轮平行打纬机构的国产双剑杆织机转速普遍不高，墙板、箱体的振动是影响打纬机构精度和寿命的重要因素之一。针对平行打纬机构进行动应力和振动分析对促进国内间隔织物双剑杆织机的高速化进程具有重要意义。目前关于打纬机构振动特性方面的研究主要集中在四连杆打纬机构分析，金玉珍等[1]对四连杆打纬机构进行数值分析，确定了喷气织机墙板的最大振动和最大应力位置。田建学等[2]通过仿真实验总结出墙板所受冲击力和变形随曲轴转速提高的变化规律。关于打纬机构动力学方面的研究主要集中在连杆打纬机构和共轭凸轮摆动打纬机构分析，沈丹峰等[3]针对墙板上曲轴孔与摇轴孔承受的支撑力，建立了动力学关系式，并对两孔的安装角度进行了优化设计。魏展等[4]应用凯恩方程建立了共轭凸轮摆动打纬机构的动力学模型。针对共轭凸轮平行打纬机构的动力学和振动研究尚处于起步阶段。

本研究对平行打纬机构及箱体进行动态静力分析、多体动力学仿真、模态分析和振动特性分析，并在仿真的过程中探究了减小箱体振动的改进方法。本研究旨在为共轭凸轮平行打纬机构的设计和优化提供参考。

1 机构原理及动应力分析

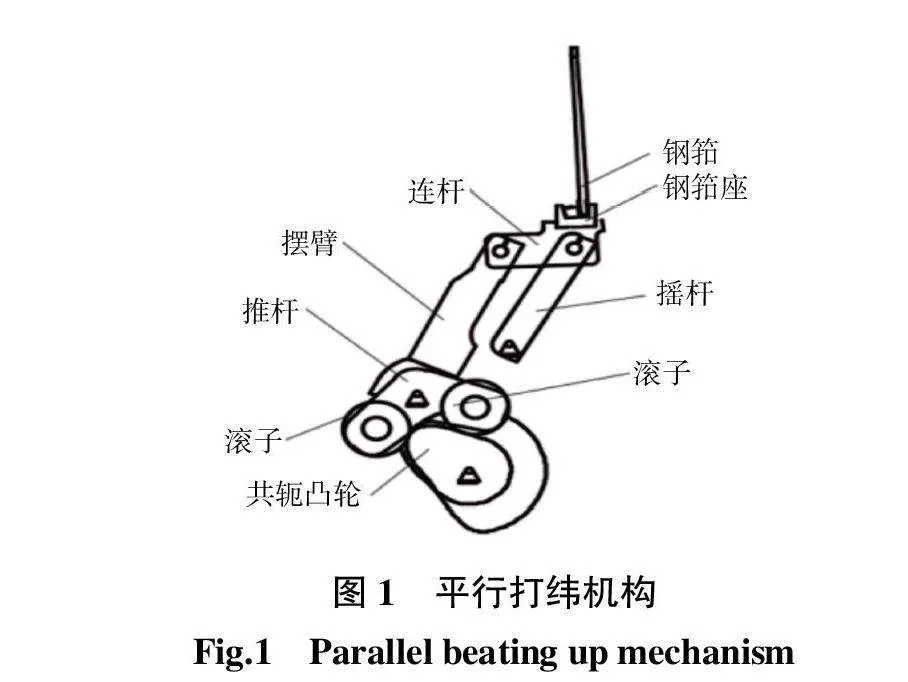
本研究以国外某先进双剑杆天鹅绒织机中的共轭凸轮平行打纬机构为分析对象，其结构原理如图1所示。

图1中，打纬过程分为3个阶段：推程阶段、回程阶段和静止阶段。共轭凸轮绕回转轴做顺时针匀速转动，其主副凸轮分别对2个滚子施加正压力，推杆与摆臂固结并绕回转轴转动，从而带动钢筘的往复摆动。静止阶段时滚子不受凸轮正压力，钢筘在打纬后死心位置静止。

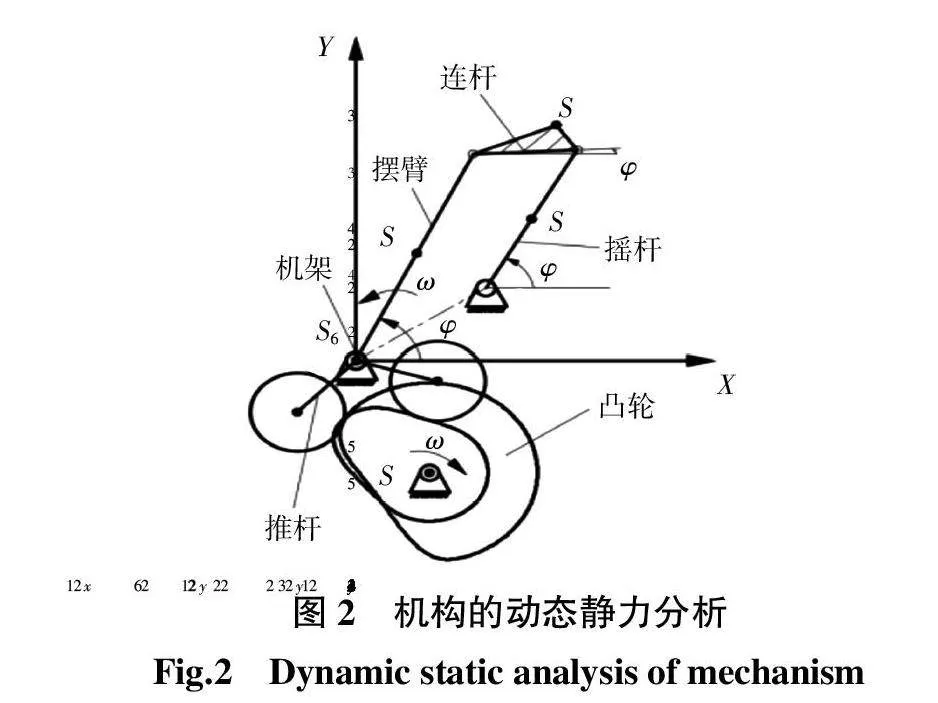
打纬机构通过回转轴孔施加给箱体的作用力是箱体振动的主要激励。对打纬机构进行动态静力分析，假设凸轮按理想规律做等速回转运动，不计入摩擦阻力、打纬阻力和凸轮滚子之间的碰撞，将推杆与滚子视为一个刚体。简化后的打纬机构动态静力分析模型如图2所示。

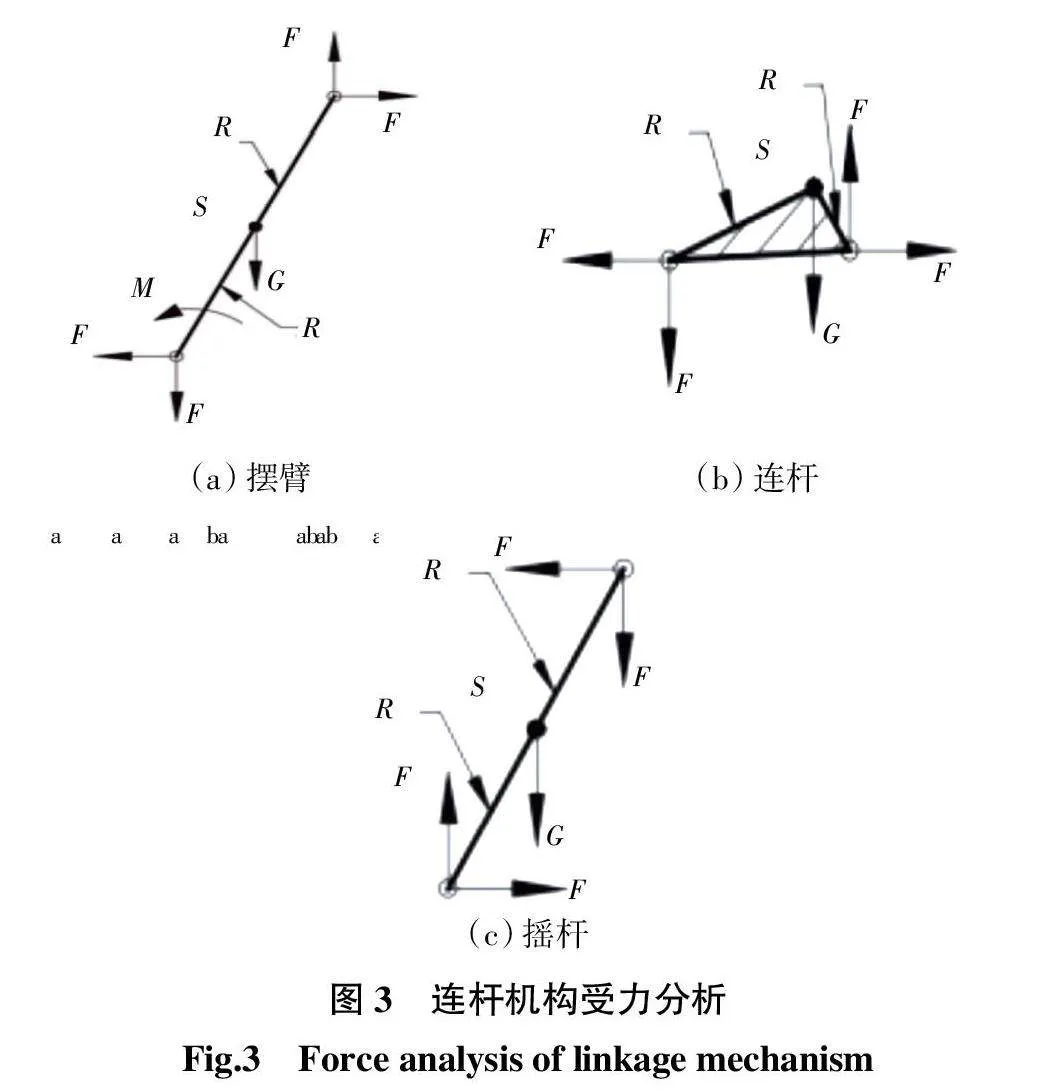
分别对从动连杆机构和凸轮机构进行动力学分析。连杆部分各构件的受力如图3所示。

图3中：Fab、Mab分别为构件a对构件b的作用力和力矩；Fba = -Fab。Rca为铰链c到构件a质心的矢量；Sa、Ga、φa分别为构件a的质心、重力和相对于整体坐标的角位移。

摆臂：

F32 x + F12 x = m2F32" y + F12 y = m2 + G2F32y R22x - F32x R22y + F12y R12 x - F12x R12y + M62 =J22（1）

连杆：

F43x - F32x = m3F43y - F32y = m3S3 + G3F43y R33x - F43x R33y - F32y R23x + F32x R23y = J33" （2）

摇杆：

F14x - F43 x = m4S4F14y - F43 y = m4S4+ G4F14y R44x - F14x R44y - F43y R34x + F43x R34y = J44" （3）

对凸轮机构进行动力学分析，各构件的受力如图4所示。

凸轮：

F15x - FRx = 0F15y - FRy =" G5Md + FRy R5py- FRx R5py = J5 5" " "（4）

式中：FR为凸轮作用在滚子上的正压力；Md为打纬机构的平衡力矩；p为凸轮与滚子的动态接触点。推程阶段主凸轮与滚子之间的接触点受力，回程阶段副凸轮与滚子之间的接触点受力。

推杆：

F16x Rx = 0F16y - FRy =" G6FRy R1px - FRx R1px - M62 = J6 6" "（5）

联立以上各式，即得到整个平行打纬机构的动态静力分析方程，其是由15个线性方程组成的方程组，共有16个未知量，为了求解，可将平衡力矩Md用实际机器测量的凸轮轴输入转矩代入近似计算，以凸轮轴转速300 r/min为例，测量凸轮轴驱动力矩一个周期内的数值记为打纬机构的平衡转矩，这样方程组未知量变为15个，可以进一步求解。将线性方程组写成矩阵的形式：

AR = B（6）

式中：A为15 × 15的已知矩阵，其中元素与构件的质心位置有关；B为15维的已知列阵，其中包含了构件所受惯性力、惯性力矩和重力；R为15维的未知列阵，其中包含了各构件所受作用力和力矩.

R = A-1B （7）

矩阵A、B中元素大都是随时间变化的，求解一次方程组只能得到某一位置的解，故还需对机构进行周期离散化，可以运用Matlab编程对m个离散位置分别求解。箱体所受支反力为箱体在回转轴孔处对其他构件作用力的反力。

2 多体动力学仿真

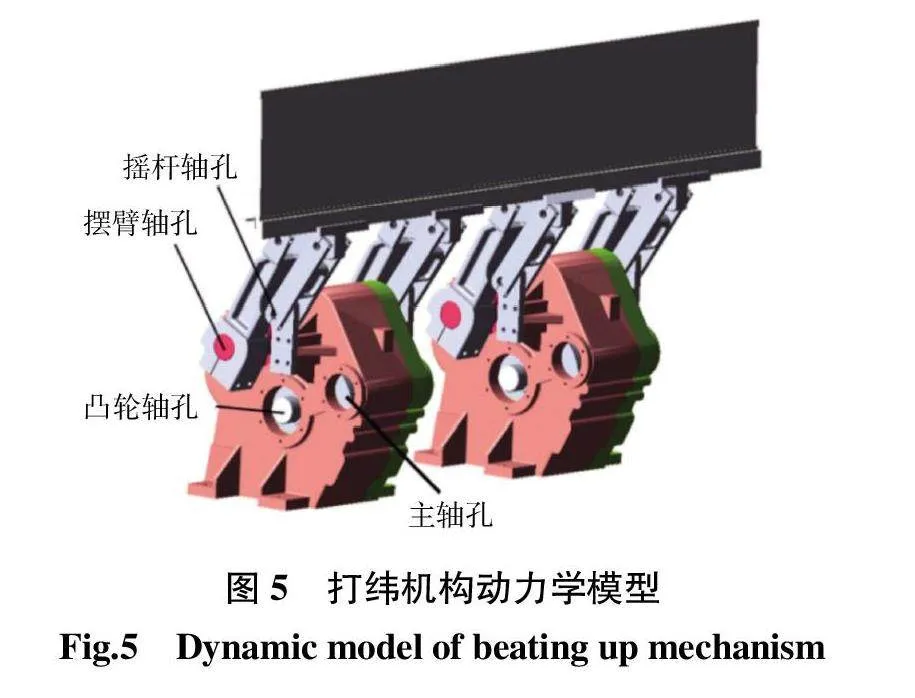
通过对机构进行多体动力学仿真得到机构的动态响应和动应力。首先对机构进行参数化设计，使用作图法，根据整机方案设计和工艺要求确定从动连杆机构的尺寸和摆臂动程，得到摆臂、连杆、摇杆的长度分别为0.29、0.11、0.2 m，摆臂角动程为33.49°。共轭凸轮从动件选用改进梯形运动规律，结合共轭凸轮机构的设计公式，运用Matlab编程得到共轭凸轮廓线数据和凸轮从动系统的几何尺寸。在SolidWorks中建立机构的虚拟样机模型，按照工程要求对机构进行结构设计，可提高仿真实验的可靠性。将三维模型文件保存为x_t文件导入ADAMS软件中，得到打纬机构的动力学模型如图5所示。

对模型进行材料设置，其中摆臂、连杆、摇杆、推杆的材料均选用球墨铸铁，凸轮选用42GrMo，滚子选用NUP圆柱滚子向心滚动轴承，材料为轴承钢。

添加约束和驱动后即可对系统进行动力学仿真和数据后处理。以凸轮轴设计转速300 r/min进行仿真，筘座线性位移和速度响应分别如图6和图7所示。

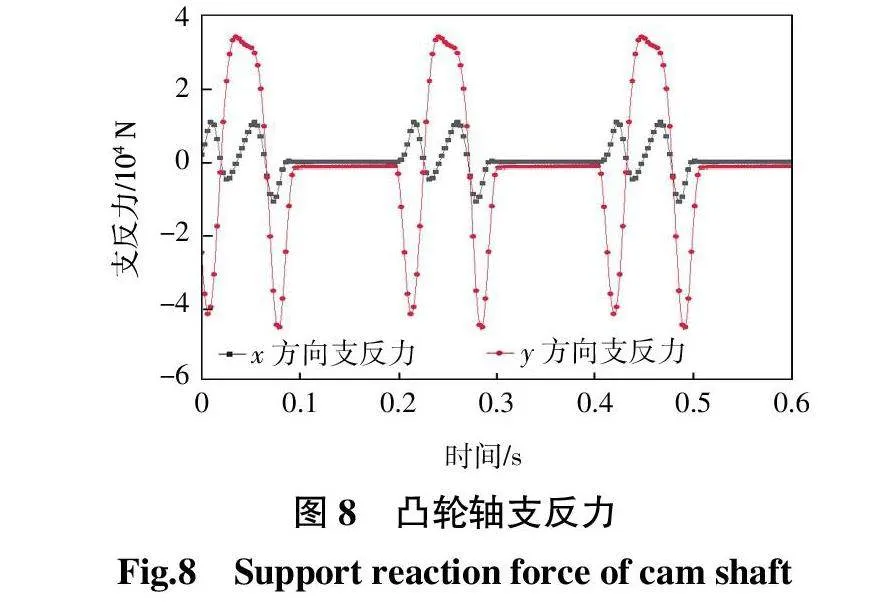
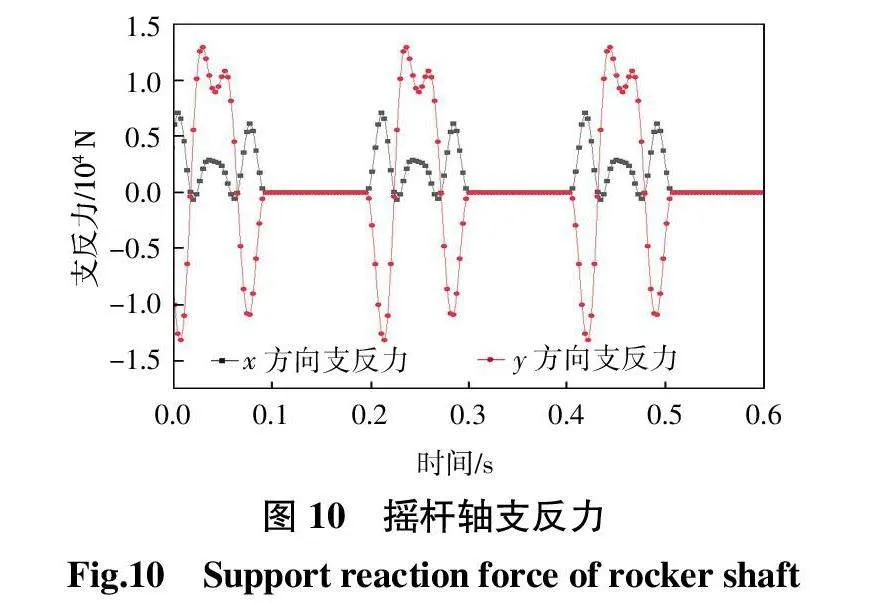
凸轮推程角回程角均为90°，则0.05 s处为打纬前死心位置，0.1 s处为后死心位置。从图6、图7可以看出，钢筘在前死心位置时x方向线性位移最大，x、y方向线性速度均为0。此时钢筘处于竖直状态并短时间内做水平运动，即实现钢筘的平行打纬运动。从而验证了理论设计的正确性和动力学模型的有效性。测量图5所示的凸轮轴孔、摆臂轴孔、摇杆轴孔处回转副的作用力的反力即为打纬箱体所受的支反力如图8—图10所示。

从图8—图10可以看出，打纬箱体回转轴孔处所受支反力变化呈现周期性，且与凸轮旋转周期一致。其中摆臂轴的支反力峰值大于凸轮轴的支反力峰值，摇杆轴支反力峰值最小。凸轮轴的最大支反力出现在回程阶段，摆臂轴和摇杆轴的最大支反力出现在推程阶段。这说明箱体在摆臂轴孔处应力冲击较大，在打纬推程阶段应力最为集中。在静止阶段3个轴孔的支反力值较小且无波动，此时各轴孔只承受机构静平衡的支反力。

3 箱体的振动特性分析

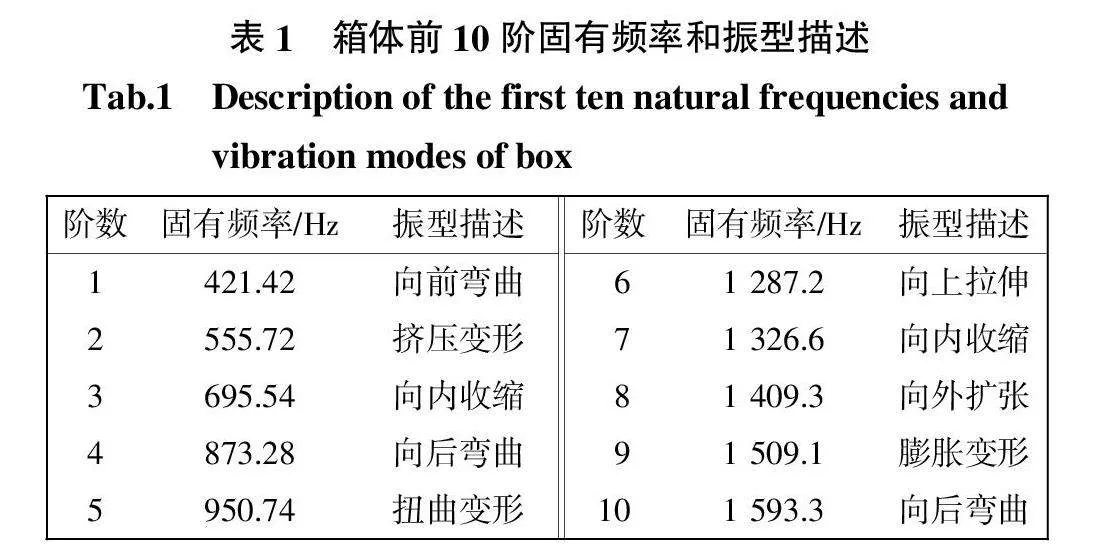
运用ANAYS软件中Workbench模块对箱体进行模态分析，将箱体模型的x_t文件导入软件，箱体材料为HT250，材料密度为7 280 kg/m3，弹性模量为1.38×1011 N/m2，泊松比0.156，划分网格，包含了375 430个节点、214 744个四面体单元。添加底面固定约束后进行模态求解，得到打纬箱体的前10阶固有频率和各阶振型描述如表1所示。

共轭凸轮通过主轴与凸轮轴的一级齿轮减速带动转动，齿轮啮合频率为：

f = （8）

式中：n为凸轮轴转速；z为从动齿轮齿数。

由机构的理论设计可得主轴与凸轮轴间减速齿轮的齿数为97/19，将表1中模态分析计算的箱体前三阶固有频率代入式（8），当凸轮轴转速为260 r/min、343 r/min、430 r/min时齿轮啮合频率分别与箱体一阶、二阶、三阶固有频率相等，引起箱体共振。目前国内双剑杆织机凸轮转速普遍在200 r/min以下，本课题来源项目的理想凸轮平行打纬目标转速为300 r/min，对于本课题所涉织机，应避免使用凸轮260 r/min这一转速工作。在后续的提速改进工程中，在不变更箱体结构时，还应避免凸轮343 r/min这一转速，以减小箱体振动对织机产生的危害。

应用ANSYS中的2次开发语言APDL模块求解柔性箱体受周期性支反力作用下的受迫振动[5-20]，将第2节动力学仿真解得的箱体在凸轮轴、摆臂轴、摇杆轴所受周期性支反力离散成一系列冲击载荷，逐个求解其动响应，在不同节点处拾取位移响应，可得最大变形出现在箱体下方节点处，最大变形为0.012 8 mm，振动变形较小，原因是此时离共振点较远，没有发生共振，在此不做深入研究。

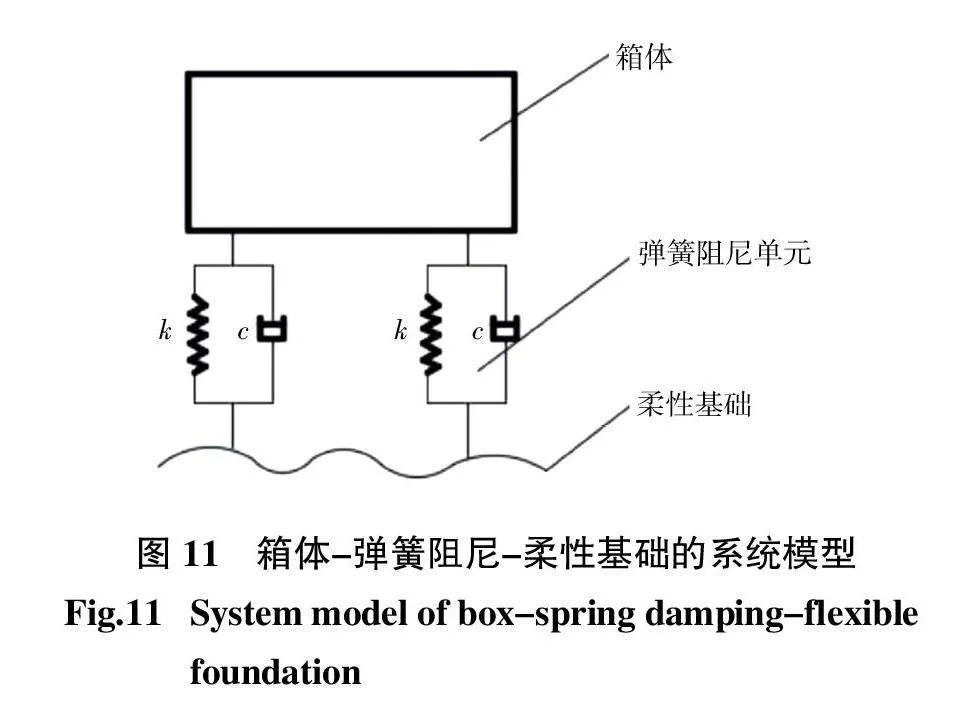
忽略箱体的内部变形，将螺栓用弹簧阻尼单元描述[7]，为了提高仿真的精确性，同时计入基础的柔性变形。整个箱体结构可以等效成一个打纬箱体—弹簧阻尼—柔性基础的耦合系统，模型如图11所示。

图11中，箱体在竖直方向上的运动为一单自由度系统受周期性激振力作用下的受迫振动。

打纬箱体所受支反力在y方向的分力引起箱体在竖直方向上的振动，设支反力y方向分力的合力为周期为T的函数F（t），将函数F（t）展开成傅里叶级数：

F（t）= a0 + （ak cos （kωt） + bk sin （kωt）） （9）

式中：a0、ak、bk为傅里叶系数。若系统的质量、刚度和阻尼分别为M、K和C，则此时受迫振动的稳态响应可以写为：

x =βkcos（kω - arctan（bk /ak） - θk）（10）

式中：βk为第k 阶响应的动力放大系数；θk为第k 阶响应与第k 阶激振力间的相位差。

由式（10）可以看出，在周期激振力作用下，系统的振动响应由无穷阶简谐振动而合成。 将箱体-基础模型导入ADAMS，基础为20 mm厚的钢板焊接而成的中空横梁底座，利用软件中的创建柔性体功能将基础柔性化，并对原有刚体模型进行覆盖替换。在箱体底部与基础间建立弹簧阻尼单元用以表述螺栓连接，根据结合面的螺栓影响锥理论用下式计算螺栓的等效刚度和等效阻尼：

K0 = π（？渍 + 2dtan γ）2K/4C0 = π（？渍 + 2d tanγ）2C/4 " "（11）

式中：φ为螺栓帽的外切圆直径；d为螺钉长度；γ为影响锥的半锥角度数，一般取为 20 °；K、C分别为结合面单位面积刚度和阻尼。

本文中箱体底面固定螺栓选用 M16x50规格的内六角圆柱头螺栓，连接方式为螺钉连接，基础底座材料为Q235。将第2节动力学仿真所求箱体所受支反力的y方向的时变激励数据以样条曲线的方式导入模型，利用软件中的AKISPL函数拟合曲线点集，在相应的轴孔添加作用力，约束箱体自由度为上下移动。运行交互仿真，忽略运动开始时载荷冲击对系统造成的影响，得到箱体在周期性支反力激振下的稳态受迫振动位移响应如图12所示。

从图12可见，箱体在周期性激振力的作用下产生周期性振动，在一个周期内，箱体的质心位移响应不只有一个波峰。正方向上的振动幅值大于负方向上的振动幅值，最大振幅出现在打纬回程阶段，为0.026 mm，且为向上振动。静止阶段箱体较为平稳，无剧烈振动。

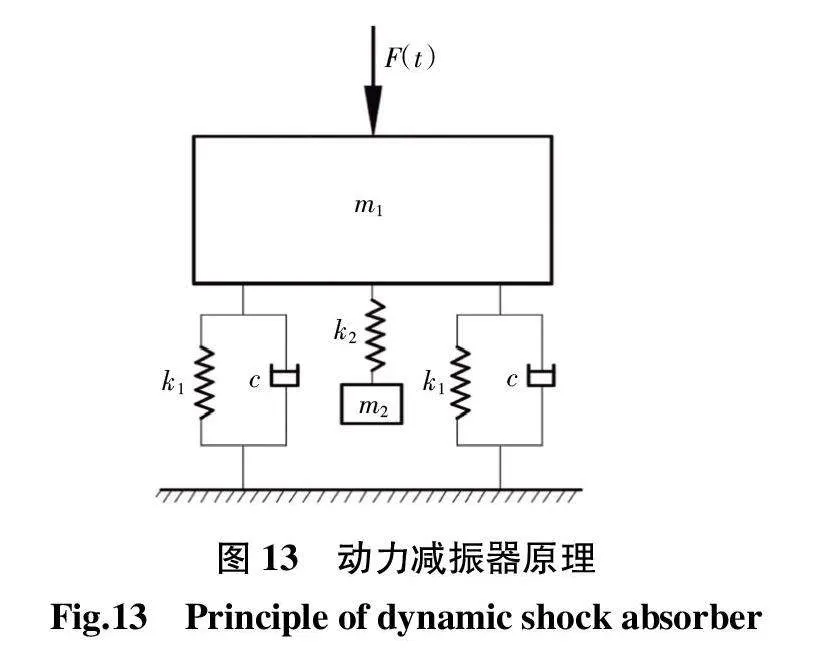
以减小箱体正方向振幅为优化目标，提出2种减振方法：第1种，由公式（10）可以看出，单自由度系统受周期性激振力时，增大系统刚度可以减小稳态振幅，增大系统刚度最直接的方法就是增加螺栓个数，对底面筋板结构进行优化并在其上增加相应螺栓孔，将底面固定螺栓由4个增加至8个。第2种是采用附加动力减振器的方法，即在箱体附加1个辅助质量，用弹性元件使之与箱体连接如图13所示。图13所示为动力减振器的原理图。

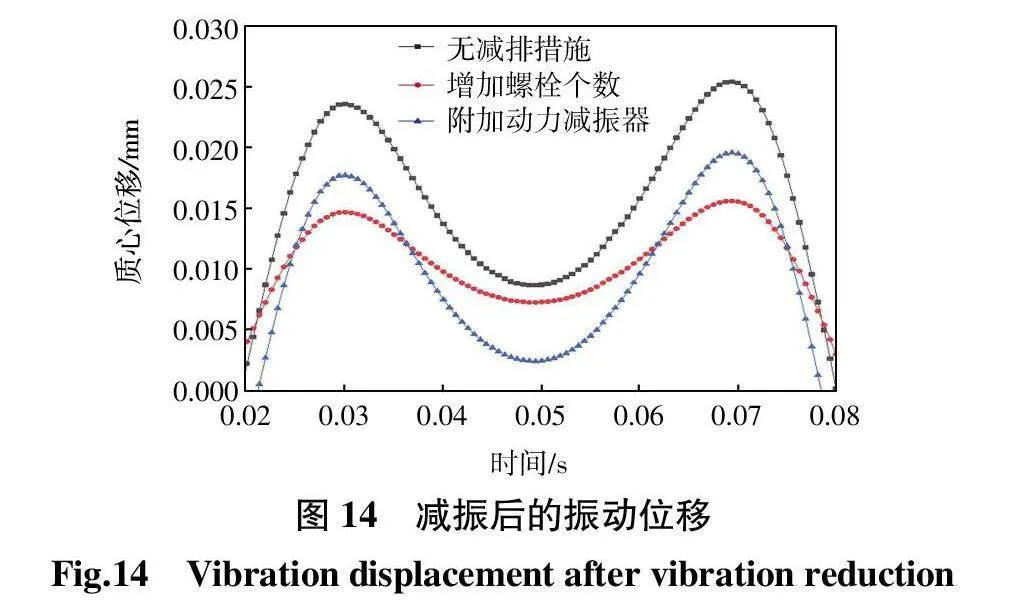
当主系统m1振动时，辅助质量m2也随之振动。利用辅助质量的动力作用，使其加在主系统上的动力与激振力互相抵消，从而使主系统的振动得到抑制。这个附加系统就称为动力减振器。本文在箱体上附加一个质量为40 kg、弹性元件刚度为2 ×105 N/mm构成的减振器。在仿真软件中对上述2种方法进行验证，得到箱体减振后稳态正方向振动位移如图14所示。

由图14可以看出，增加螺栓个数和附加动力减振器的措施对箱体正方向的振幅都有一定的抑制作用，相较不进行减振的原系统，增加螺栓个数后箱体振幅减小38%，附加动力减振器后振幅减小23%，但在实际的工程应用中，箱体结构不易变更，增加螺栓个数的方法具有局限性，且螺栓个数过多会造成螺栓功能的冗余，并对安装造成不便。相较而言，附加动力减振器的方法可根据实际的减振效果调换附加质量和弹性元件，具有灵活性较强的优势。

4 结 论

针对共轭凸轮平行打纬机构箱体的动应力和振动特性进行理论分析和仿真实验分析，得出以下结论：

（1） 摆臂轴孔处箱体所受支反力峰值最大，打纬推程阶段箱体的受力最为集中。

（2） 当凸轮轴转速为260 r/min时齿轮啮合频率与箱体一阶固有频率相等，会引起箱体共振，应避免使用这一转速进行工作。研究结果对实际的工程项目具有一定的指导意义。

（3） 箱体在周期性支反力的作用在竖直方向上产生周期性振动，最大振幅发生在打纬回程阶段，为0.026 mm。仅从减小箱体正方向振幅的角度出发，增加螺纹个数和附加动力减振器均有利于改善箱体的振动特性，增加螺栓个数后箱体振幅减小38%，附加动力减振器后振幅减小23%。研究结果对共轭凸轮平行打纬机构箱体的设计和优化提供了参考。

参考文献：

[1]" " 金玉珍， 胡小冬， 林培峰， 等. 喷气织机打纬机构及墙板的振动特性[J]. 纺织学报， 2016， 37（7）： 131-136， 141.

JIN Y Z， HU X D， LIN P F， et al. Vibration characteristics of wallboard and four-bar linkage beating-up mechanism of air-jet loom[J]. Journal of Textile Research， 2016， 37（7）： 131-136， 141 （in Chinese）.

[2]" " 田建学， 张珏， 屈晓渊， 等. 基于计算机仿真技术的织机打纬机构设计[J]. 西北大学学报（自然科学版）， 2015， 45（6）： 942-946.

TIAN J X， ZHANG J， QU X Y， et al. Design of loom′s beating-up mechanism based on computer simulation technology[J]. Journal of Northwest University（Natural Science Edition）， 2015， 45（6）： 942-946（in Chinese）.

[3]" " 沈丹峰， 赵宁， 张华安， 等. 织机四连杆打纬机构对主墙板的动应力分析[J]. 纺织学报， 2013， 34（1）： 110-115.

SHEN D F， ZHAO N， ZHANG H A， et al. Dynamic stress analysis of four-bar linkage beating-up mechanism on loom wallboard[J]. Journal of Textile Research， 2013， 34（1）： 110-115（in Chinese）.

[4]" " 魏展， 金国光， 袁汝旺， 等. 高速共轭凸轮打纬机构柔性动力学分析[J]. 机械工程学报， 2017， 53（3）： 81-89.

WEI Z， JIN G G， YUAN R W， et al. Flexible dynamic analysis of high-speed conjugate cam beating-up mechanism[J]. Journal of Mechanical Engineering， 2017， 53（3）： 81-89 （in Chinese）.

[5]" " FU S P， LUO S M， HUANG H L. Analysis of transmission box vibration characteristics under random road torsional excitation[J]. Proceedings of the Institution of Mechanical Engineers， Part D： Journal of Automobile Engineering， 2022， 236（12）： 2582-2597.

[6]" " WU H， WU P B， XU K， et al. Research on vibration charac-teristics and stress analysis of gearbox housing in high-speed trains[J]. IEEE Access， 2019， 7： 102508-102518.

[7]" " 伍良生， 马淑慧， 屈重年， 等. 弹簧-阻尼动力学单元螺栓连接结合面研究[J]. 机械设计与制造， 2014（1）： 4-6.

WU L S， MA S H， QU C N， et al. The study of bolted joint surface of the spring-damping dynamics unit[J]. Machinery Design amp; Manufacture， 2014（1）： 4-6 （in Chinese）.

[8]" " LI M M， LIU Q W， DAI G H， et al. Vibration transfer path analysis of double-layer box for marine reducer[J]. Journal of Vibration Engineering amp; Technologies， 2021， 9（6）： 1077-1089.

[9]" " 胡玉飞，张建超，陈湛，等.内部激励下高速动车齿轮箱振动响应评估[J]. 北京交通大学学报，2022，46（4）：148-156.

HU Y F， ZHANG J C， CHEN Z，et al. Evaluation of vibration response of high-speed train gearboxes under internal excita-tion[J]. Journal of Beijing Jiaotong University， 2022， 46（4）：148-156（in Chinese）.

[10]" YU X L， HUANGFU Y F， YANG Y， et al. Gear fault diagno-sis using gear meshing stiffness identified by gearbox housing vibration signals[J]. Frontiers of Mechanical Engineering， 2022， 17（4）： 57.

[11]" 黄晓丹， 裴帮， 关鹤， 等. 基于刚柔耦合的地铁齿轮箱故障仿真研究[J]. 机械传动， 2021， 45（10）： 137-143， 156.

HUANG X D， PEI B， GUAN H， et al. Fault simulation resea-rch of metro gearbox based on rigid-flexible coupling[J]. Jour-nal of Mechanical Transmission， 2021， 45（10）： 137-143， 156（in Chinese）.

[12]" 刘辉， 张喜清， 项昌乐. 多源动态激励下变速箱箱体结构的动态响应分析[J]. 兵工学报， 2011， 32（2）： 129-135.

LIU H， ZHANG X Q， XIANG C L. Dynamic response analysis of gearbox housing under multi-source dynamic excitation[J]. Acta Armamentarii， 2011， 32（2）： 129-135（in Chinese）.

[13]" SONG L M. Experimental research on vibration and noise re-duction of vehicular vacuum circuit breaker′s equipment box[J]. Science Discovery， 2018， 6（2）： 85.

[14]" SEON S O， KIM J O. Vibration and acoustic characteristics depending on housing structures of ultrasonic sensors[J]. Tra-nsactions of the Korean Society for Noise and Vibration Engi-neering， 2019， 29（2）： 157-165.

[15]" 任亚峰， 常山， 刘更， 等. 齿轮-箱体-基础耦合系统的振动分析[J]. 华南理工大学学报（自然科学版）， 2017， 45（5）： 38-44.

REN Y F， CHANG S， LIU G， et al. Vibration analysis of gear-housing-foundation coupled system[J]. Journal of South China University of Technology（Natural Science Edition）， 2017， 45（5）： 38-44（in Chinese）.

[16]" VIDHYA B， SRINIVAS K N. Vibration analysis including sta-tor， rotor， housing and dynamic response analysis of Flux Re-versal Generator[J]. Journal of Electrical Systems and Informa-tion Technology， 2018， 5（2）： 144-157.

[17]" 黄冠华， 王兴宇， 梅桂明， 等. 内外激励下高速列车齿轮箱箱体动态响应分析[J]. 机械工程学报， 2015， 51（12）： 95-100.

HUANG G H， WANG X Y， MEI G M， et al. Dynamic respo-nse analysis of gearbox housing system subjected to internal and external excitation in high-speed train[J]. Journal of Me-chanical Engineering， 2015， 51（12）： 95-100 （in Chinese）.

[18]" 王强龙， 李耀彬， 伞晓刚， 等. 螺栓连接条件下结构振动模态的时频分析方法[J]. 机械设计与制造， 2016（7）： 72-76.

WANG Q L， LI Y B， SAN X G， et al. Model analysis of struc-ture with bolt connections using the method of transient respo-nse and frequency transformation[J]. Machinery Design amp; Ma-nufacture， 2016（7）： 72-76（in Chinese）.

[19]" LEE T H. Muscular activity and acceleration of box vibration in manual holding tasks： Effects of load and height of the load′s center of gravity[J]. International Journal of Occupational Safe-ty and Ergonomics， 2020， 26（1）：15-19.

[20]" 周香琴， 杨胜皎， 王琴龙， 等. 剑杆织机惯性载荷变化规律及提速试验[J]. 纺织学报， 2017， 38（8）：144-149.

ZHOU X Q， YANG S J， WANG Q L， et al. Inertial load change rule and speed increasing test of rapier loom[J]. Journal of Textile Research， 2017， 38（8）： 144-149（in Chinese）.

本文引文格式：

杨建成，刘艳哲，黄子文，等. 间隔织物双剑杆织机平行打纬机构箱体的振动分析[J]. 天津工业大学学报，2024， 43（3）： 82-88.

YANG J C， LIU Y Z， HUANG Z W， et al. Vibration analysis of parallel beating up mechanism box of double rapier loom for spacer fabric[J]. Journal of Tiangong University， 2024， 43（3）： 82-88（in Chinese）.