高频双频Buck变换器平面集成磁件优化设计

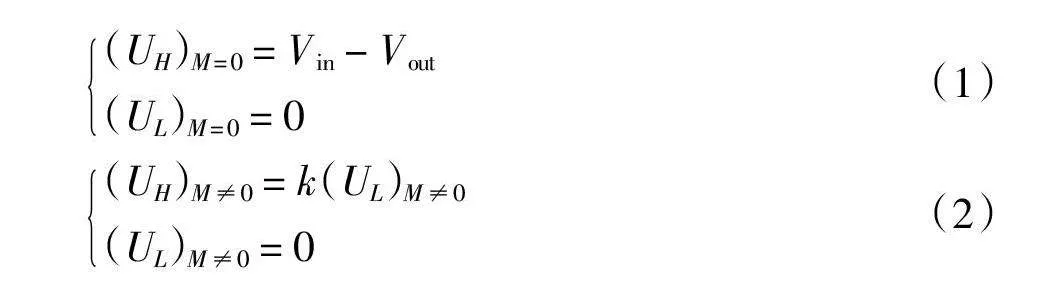
摘" " 要： 针对目前开关器件和磁性元件性能不足导致双频Buck变换器的效率和功率密度低的问题，研究了一种高效高功率密度的双频Buck变换器。变换器将工作在连续导通（CCM）模式，采用解耦合的平面集成电感器完成系统磁元件的集成，结合磁件的集成方法、有限的PCB层数和变换器的特性给出双频Buck变换器的参数，然后，提出了一种双频Buck变换器平面磁件的设计方法，并完成系统磁元件的优化设计。最后，基于第3代半导体SiC器件以及平面集成磁件，设计了额定功率200 W、开关频率400 kHz的双频Buck变换器。结果表明：该变换器峰值效率将达到96.1%，功率密度为46.1 W/in3（1 in = 25.4 mm），验证了双频Buck变换器设计方法的正确性和有效性。

关键词： 双频Buck变换器； 平面磁件； 高频高效高功率密度； SiC器件

中图分类号： TN624" " " " " 文献标志码： A" " " " " " " " 文章编号： １６７１－０２４Ｘ（２０24）０3－００66－09

Optimal design of planar integrated magnetics for high-frequency

double-frequency Buck converter

GAO Shengwei， YU Guanheng， ZHAO Hongyu

（Tianjin Key Laboratory of Intelligent Control of Electrical Equipment， Tiangong University， Tianjin 300387， China）

Abstract： In order to solve the problem that the efficiency and power density of double frequency Buck converters are still relatively low， which are caused by insufficient switching devices and magnetic components， a double-frequency Buck converter with high efficiency and high power density is proposed. Converter will work in CCM mode， using decoupled planar integrated inductors to complete the integration of the magnetic components of the system. Combined with the integration method of magnetic components， the limited number of PCB layers and the characteristics of the converter， the parameters of the double frequency Buck converter are given. Then， a design method of planar magnetic components is proposed， and the optimal design of the magnetic components of the system is completed. Finally， based on the third-generation semiconductor SiC devices and planar integrated magnetic components， a double-frequency Buck converter with a rated power of 200 W and the switch frequency of 400 kHz is designed. The results show that the peak efficiency of the converster will reach 96.1%， and the power density will be 46.1 W/in3（1 in = 25.4 mm）. These confirm the correctness and effectiveness of the double-frequency Buck converter design method.

Key words： double frequency Buck converter； planar magnetics； high frequency， high efficiency and high power density； SiC devices

双频Buck（double frequency Buck，DFBuck）变换器是由2个不同频率的Buck变换器级联而成的，在拥有高频Buck变换器输出特性的同时，只承担低频Buck的开关损耗，能够在高开关频率下为系统带来更高质量的电能[1-3]。在未来供电系统中，对DC-DC变换器的频率、效率以及功率密度要求越来越高，高频化、平面化、集成化成为未来DC-DC变换器研究目标[4]。目前DFBuck变换器大多采用Si器件，工作频率仍然停留在25～100 kHz[6-8]，功率密度和效率仍然难以满足供电系统的需求，也难体现DFBuck变换器在高频率工作时的优势。第3代半导体器件（如SiC器件）的发展使得DFBuck变换器工作在更高的频率成为可能，也将提高变换器的性能和功率密度。在高频下，传统的绕制磁件正逐渐被具有平面磁芯和印刷电路版（PCB）绕组的平面磁件代替，这种磁件存在可重复高、体积小、功率密度高等优点。平面磁件设计的合理性对DC-DC变换器而言是十分重要的，因为不合理的平面磁件存在产热高、损耗大等问题，将影响变换器的正常工作[9-12]。

目前学者针对高频高效的变换器以及平面磁件的优化做出了大量的研究。文献[13]针对低压大电流场合下的LLC谐振变换器，引入矩阵变压器来减小磁元件的电流，具有PCB绕组的变压器设计在UI磁芯上，同时提出了针对变压器的损耗和磁件体积的优化设计方法，完成了系统设计；文献[14]在文献[13]的基础上，针对磁件和变换器的结构进行了优化，使得变换器的性能得到提升，但文中对于变换器的研究以及磁元件的优化方法并不适用于DFBuck变换器。文献[15]提出了一种基于响应面方法（MLM），通过有限元法遍历变压器的变量得到平面变压器的参数；文献[16]又将此方法推广到平面电感上，受仿真速度的限制，此方法不适用于实际设计中。文献[17]通过对两级式DC-DC进行分析，给出了变换器的参数以及磁元件的结构，并给出了一套耦合集成的平面电感器系统的优化方法，使得电感之间的耦合系数到达预期的值。此方法并不适用于DFBuck变换器和平面解耦集成磁件的优化设计，但却为非隔离变换器以及平面集成电感的研究提供了参考。文献[18]针对多相CLLC谐振变换器分析，给出了系统参数以及控制方法，在磁元件上，针对平面矩阵变压器单层多匝绕组进行研究，并给出了一套优化方法，但此方法只适用于正弦波激励下的线圈，另外该文也没有考虑同层多匝线圈间的邻近效应。文献[19]通过建立变压器Dowell模型，并通过傅里叶分解的方法，得到了任意波形激励下的PCB直交流阻抗之间的比例关系，文献[20]将此方法推广至平面电感的设计，同时对于高频导线间的集肤效应和邻近效应进行分析，这为DFBuck变换器平面集成磁件的设计提供了可能。

本文针对高频高效的DFBuck变换器及其平面电感器进行研究。首先，针对DFBuck变换器的特性分析，选择合适的耦合方式以及磁集成方法将DFBuck变换器的高低频电感集成在一个平面磁芯上，结合有限的PCB层数以及变换器特性给出DFBuck变换器系统参数；然后，综合分析影响磁元件损耗的因素，完成平面磁件的优化设计；最后，基于此磁件以及第3代半导体SiC器件，完成输入范围64～160 V、输出电压48 V、额定功率200 W的DFBuck变换器，并完成实验验证。

1 DFBuck参数分析

1.1 解耦集成的优势

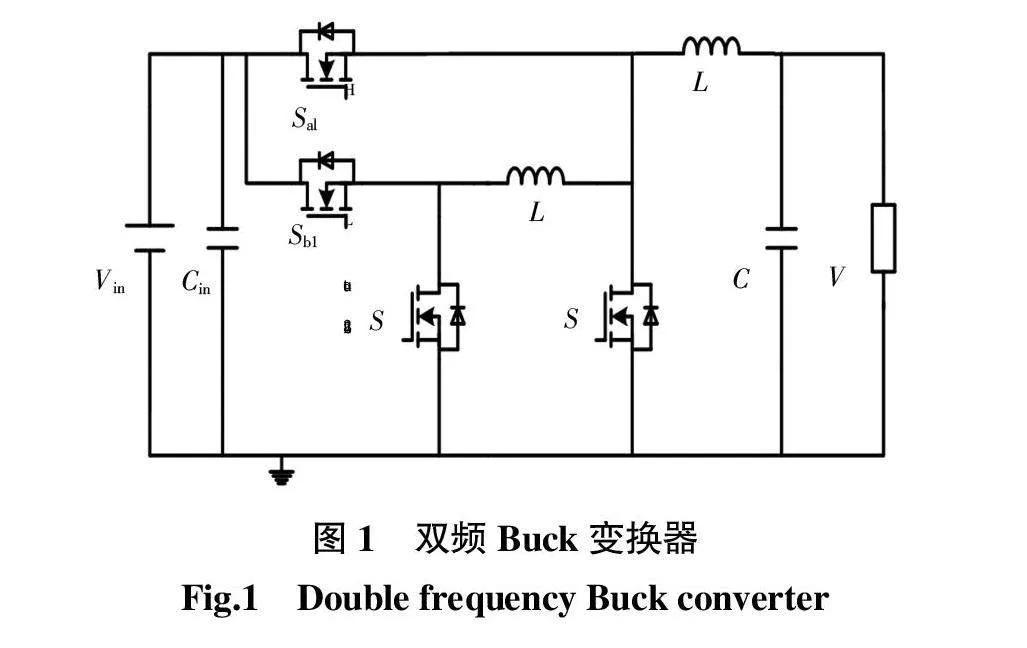
DFBuck变换器的结构如图1所示。

DFBuck变换器可工作在连续导通（CCM）以及断续导通（DCM）模式下，由于DFBuck变换器只承担低频单元的开关损耗，系统的总开关损耗较低，DCM模式降低变换器开关损耗的优势并不明显，且会降低系统稳定性，增加控制策略的难度。为保证系统的稳定性，简化控制策略，本文的DFBuck变换器在全输入电压范围内工作在CCM模式，电感电流的纹波系数将发生改变，这将降低平面电感器的设计难度，提高变换器的效率。图1中：Sa1、Sa2为高频单元的功率器件；Sb1、Sb2为低频单元的功率器件；Vin为输入电压；Vout为输出电压。DFBuck变换器的高低频单元存在2个大小不同的电感，LH为高频电感，LL为低频电感，在提高变换器的功率密度上，集成电感的概念目前得到广泛的应用，通过集成电感能够减小磁芯的数量和体积，减小变换器的磁损，提高变换器的效率及功率密度。

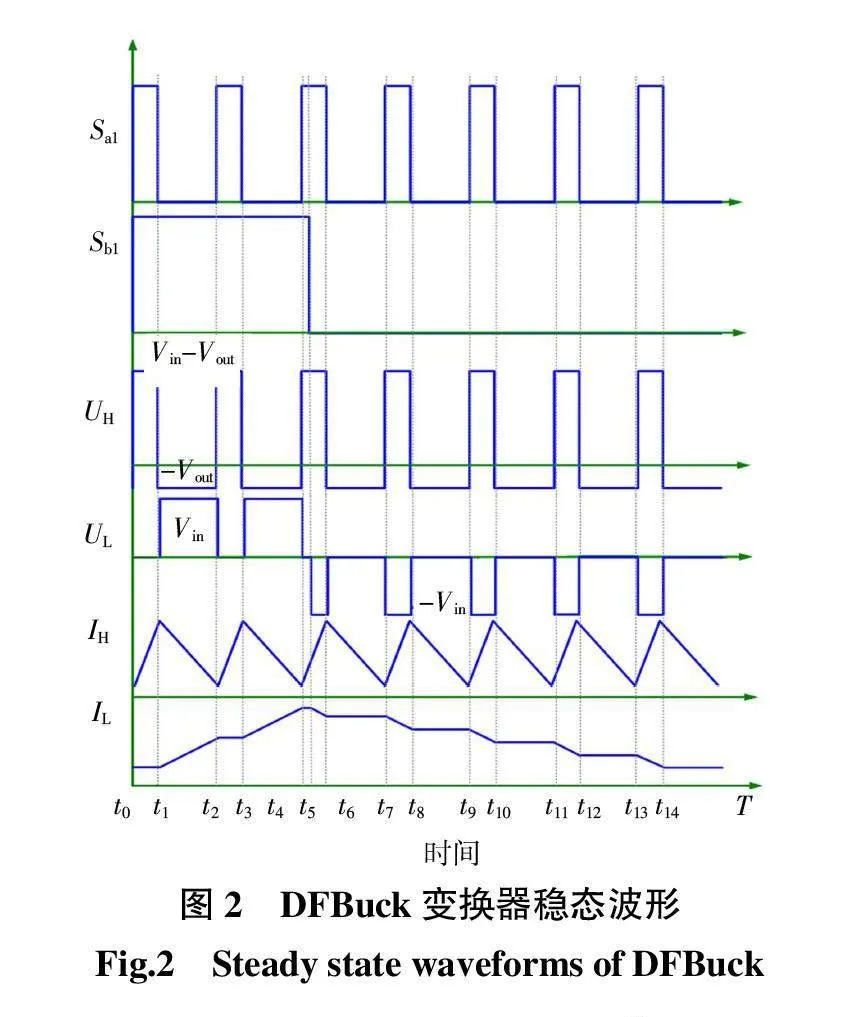
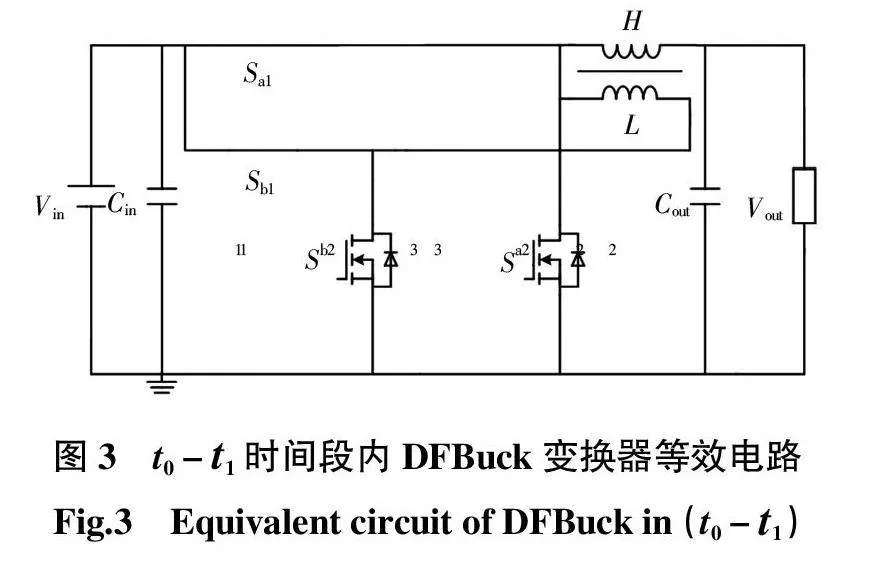
图2为输入电压为160 V时DFBuck变换器Sa1和Sb1的驱动信号（高低频单元的开关频率与下文一致）。图2中：UH、UL为高低频单元的电感耦合系数为0时，电感两端的电压波形；IH、IL为高低频单元的电感耦合系数为0时的电流波形。t0 - t1时间段DFBuck变换器的等效电路如图3所示。图3中，Sa1、Sb1开通，此时高低频电感两端电压UH（M = 0）、UL（M = 0）的值为式（1），当高低频电感之间相互耦合时，高低频电感两端电压将相互感应，设感应系数为k0，此时高低频电感两端电压UH（M≠0）、UL（M≠0）的值为式（2），此时DFBuck变换器将失去电能转化的功能。通过仿真表明，DFBuck变换器高低频耦合时，即使针对高低频电感电流进行控制，其性能也与单个高频Buck一致。高低频电感耦合将破坏DFBuck的特性，电感与电感的解耦集成成为集成DFBuck变换器高低频电感的方法。

（UH）M = 0 = Vin - Vout（UL）M = 0 = 0（1）

（UH）M ≠ 0 = k（UL）M ≠ 0（UL）M ≠ 0 = 0（2）

图4为电感与电感的解耦集成方法。

目前学者提出了大量电感与电感的解耦集成方法，文献[7]提出了如图4（a）所示的磁件结构，此方法将高频电感绕制在Ⅰ、Ⅱ柱上，将低频电感绕制在Ⅲ柱上，记为IM1。文献[8]提出了将一个电感绕制在Ⅰ柱上，另一个电感绕制在Ⅱ、Ⅲ柱，如图4（b）的磁集成方法，记为IM2。不同的磁元件会影响系统的性能，磁元件绕制结构的不同会影响磁元件的磁链，从而影响变换器的性能，不同磁元件在Ⅰ、Ⅱ、Ⅲ柱上的磁链为φ1、φ2、φ3，Ⅰ、Ⅱ柱的截面积为Ⅲ柱的1/2，每个磁柱上开相同的气隙，得到φ1、φ2、φ3的表达式为式（3）和式（4）：

IM1：φ1 = φH - φL /2φ2 = φH + φL /2φ3 = φL（3）

IM2：φ1 = φHφ2 = 2φL /2 - φH /3φ3 = 2φH/3 + φL /3（4）

式中：φH、φL分别为高、低频电感的磁链，对于IM1，其大量的磁链集中在截面积较小的Ⅱ柱上，这容易造成磁元件的饱和，降低系统稳定性，影响双频变换器的特性。另外，相距较远的低频电感的连接也会增大平面电感器的面积。IM2的磁链分布由下文得出，其磁链分布更加均匀，不易饱和，相邻两磁柱上的低频电感也将减小磁元件的面积，并且变换器的稳态与动态特性与分立磁件一致，因此DFBuck变换器选择图4（b）所示的磁集成方法。

1.2 IM2解耦条件

图5为IM2磁路的等效模型。

图5中：NH代表H的匝数；NHIH为高频电感的磁动势；N1代表L在Ⅱ柱的匝数；N1IL为磁动势；N2代表L在Ⅲ柱的匝数；N2IL为磁动势；R1、R1、R2分别为磁柱Ⅰ、Ⅱ、Ⅲ的磁阻（Ⅰ、Ⅱ柱的气隙磁阻和磁芯磁阻相同，均用R1表示），得到Ⅰ、Ⅱ、Ⅲ柱上磁密的表达式为式（5）：

？椎1 = NH IH - NL1 IL + NL2 IL？椎2 = -NH IH + NL1 IL + NL2 IL？椎3 = NH IH "+ NL1 IL + 2NL2IL？驻 = 2R12 + R1R2（5）

由法拉第电磁感应定律可以得到磁元件的磁通变化率与系统电感电流变化率的关系如式（6）所示：

UH = NH = LHH + MHLUL = NL1 + NL2= MLH + LLL（6）

式中：LHH、LLL分别为H和L的自感；MLH、MHL为高低频电感之间的互感。结合式（5）—（6），得到MHL与MLH的值为式（7）：

MHL = MLH = （7）

当满足N2R2 = N1R1时，高低频电感完全解耦，对于EE磁芯，需保证Ⅲ柱截面积为边柱的2倍，并且N1 = 2N2时，解耦成立。

1.3 DFBuck变换器的参数分析

本文研究的DFBuck变换器的输入电压为64 ～160 V，输出电压为48 V。为保证变换器有较高的功率密度，高频部分开关频率fH定为400 kHz，为保证磁件正常工作，减小磁元件的损耗，磁芯采用平面EE32磁芯，以6层PCB线圈作为磁件绕组，磁件气隙取0.2 mm。为保证高低频单元解耦并充分利用PCB，NH、N1、N2的值分别为6、12、6。图6为IM2的电容回转器模型。

通过电容回转器模型进行分析，可以得到高低频电感与线圈匝数关系如式（8），为简便分析，暂不考虑杂散磁通。

H = NH2（（C1 //Cg1）//（（C2 //Cg2） + （（C3 //Cg3）））L = （N1 + N2）2（（C2 //Cg2）//（（C3 //Cg3））C = （8）

式中：μ0为真空磁导率；μr为磁芯磁导率；Ci、Cgi（i=Ⅰ，Ⅱ，Ⅲ）分别为磁柱及中间气隙的等效磁导；lg为气隙长度；Ai（i =Ⅰ，Ⅱ，Ⅲ）为Ⅰ、Ⅱ、Ⅲ磁柱截面积。通过上式可得，高频电感值为12 ？滋H，低频电感值为84 ？滋H。为确保DFBuck变换器特性，需保证高低频单元的电感电流的纹波系数相同[6]，通过式（9）得到系统低频部分的开关频率fL为400/7 kHz，电感电流的纹波系数k与高频单元一致性为0.87。

2kfLIoutL gt; Vin D（1 - D）（9）

式中：Iout为输出电流。最终得到了双频变换器的参数以及平面磁元件的结构。

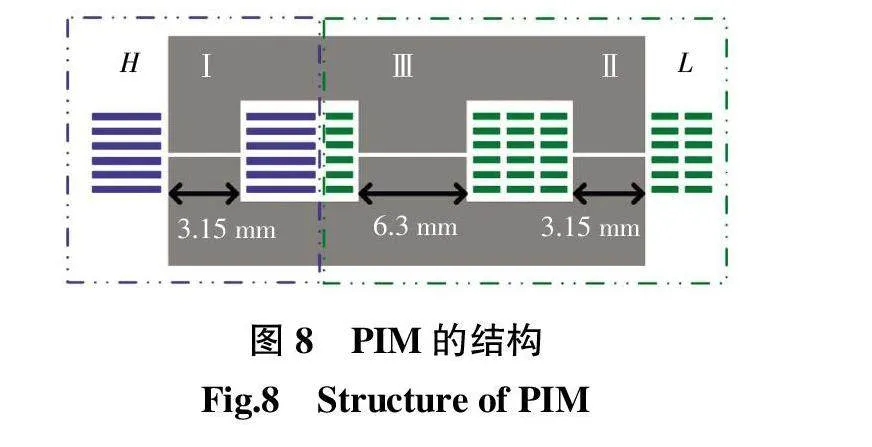
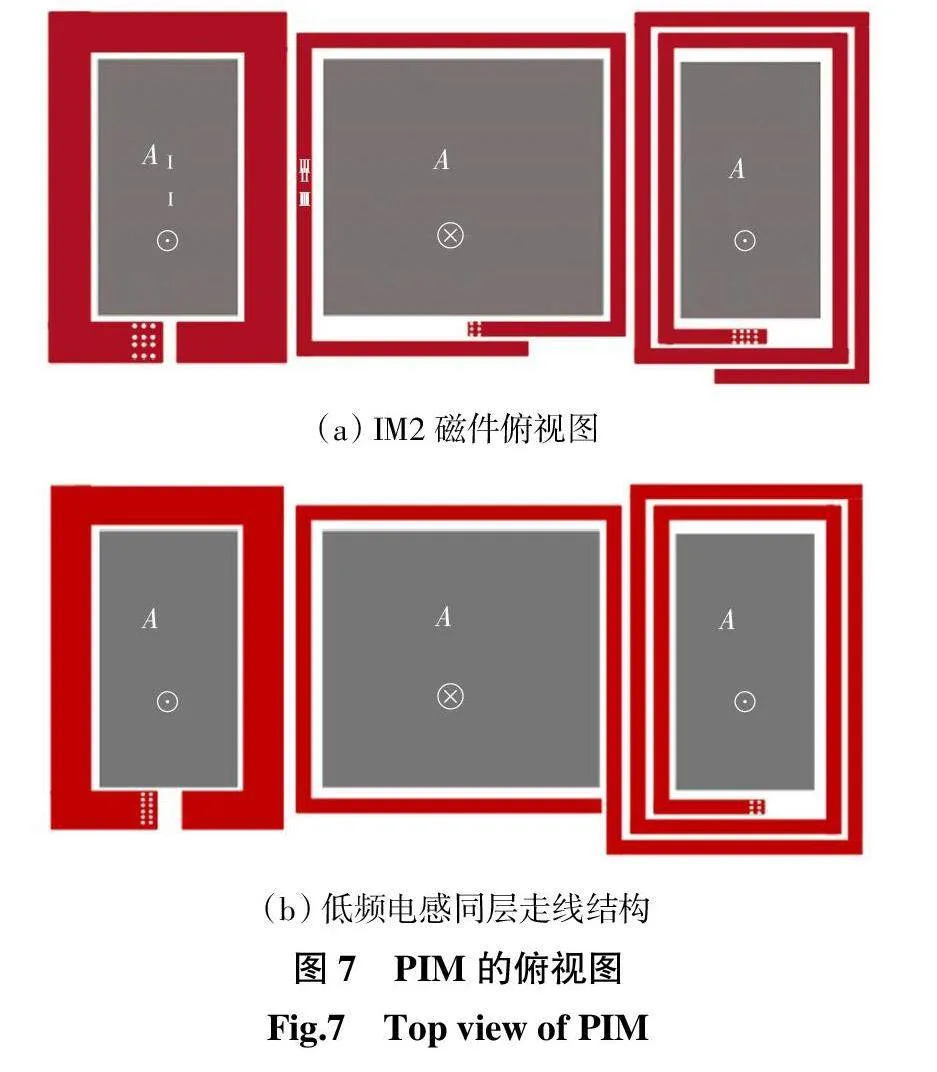
图7为PIM的俯视图。

图7（a）为具有PCB线圈和平面磁芯的IM2磁件（planar integrated magnetic components，PIM）的俯视图，其电流的方向与绕制磁件的电流方向一致，此结构存在低频电感通孔数量较多的问题，这将造成大量的通孔损耗，于是提出图7（b）所示的低频电感同层走线的结构，此结构将减小磁件的通孔损耗，进一步提高系统的效率。

上文首先针对DFBuck变换器的特性进行分析，选择合适的耦合方式以及磁集成方法完成高低频电感的磁集成；之后分析集成后的磁元件，得到其满足系统要求的条件；然后基于磁件的集成方法，DFBuck变换器的特性和有限PCB层数，分析变换器的参数；最后针对磁元件PCB的走线方式进行改进，得到最终磁元件的正视图如图8所示。

2 平面集成磁件的优化设计

系统的平面磁件决定着系统的效率和功率密度，不合理的磁件将产生大量的损耗以及温升，针对平面磁件的绕组和磁芯进行分析，对提高变换器效率十分重要，因此具备2个不同频率电感的平面集成电感器的优化成为研究重点。

2.1 PIM绕组铜厚分析

PIM绕组铜厚影响着铜导线的截面积、线圈中磁动势的分布、绕圈的集肤效应以及线圈之间的邻近效应，进而影响平面磁件中直流阻抗与交流阻抗。由文献[20]可知，对于高频率的PCB线圈，线圈的直流阻抗Rdc和交流阻抗Rac之间存在比例FR，在考虑绕组本身的集肤效应以及绕组间的邻近效应时，交流阻抗Rac分解为由集肤效应产生的阻抗Rskin和由邻近效应产生的阻抗Rproximity，Rskin、Rac、Rproximity、Rdc之间满足式（10）：

Rac = FR·Rdc = Rskin + Rproximity =

（FRskin + FRproximity）Rdc（10）

式中：FRskin与FRproximity分别为Rskin和Rproximity与Rdc之间的比值，FRskin和FRproximity的表达式为：

FRskin = "=" " "（）FRproximity = "=" " " （） （11）

式（11）中Δ满足式（12）：

？驻 = （12）

式（11）—（12）中：h为PCB厚度；？驻为集肤深度；m为PCB的层数；ρCu为铜的电导率；fx代表频率；n为谐波的次数。其中低频电感的集肤深度ΔL约为278 μm，高频电感的集肤深度ΔH约为105 μm。通过式（11）和式（12）可以得到不同厚度不同频率的铜导线直流阻抗Rdc与交流阻抗Rac之间的比例关系。

2.2 PIM的阻抗分析

铜线直流阻抗的表达式为式（13）：

Req = ρCu =" ρCu（13）

式中：lCu为铜线长度；ρCu为铜线电导率；S为铜线截面积；wCu为铜线宽度；h为铜线厚度。h、lCu、wCu为影响绕组阻抗的变量，影响磁件损耗，合理地设计h、lCu、wCu将降低磁件的绕组损耗。

PIM的绕组由6层走线一致的PCB组成，在本节将针对第1层线圈优化，第1层线圈的俯视图如图9所示。

图9中：Ⅰ柱为单匝高频线圈；Ⅱ柱为两匝低频线圈；Ⅲ柱为单匝低频线圈；高频电感直流阻抗Rdch为Ⅰ柱线圈直流阻抗，即为Rh1。低频电感直流阻抗Rdcl为Ⅲ柱线圈直流阻抗Rl1以及Ⅱ柱两匝线圈直流阻抗Rl2、Rl3的和。根据式（6），可以得到Rdch、Rdcl与lCu、wCu、h的关系如式（14）—（16）：

Rh1 = 2？籽Cu" Rl1 = 2？籽Cu" Rl2 = ？籽CuRl3 = 2？籽Cu （14）

Rdch = Rh1" Rdcl = Rl1 + Rl2" + Rl3 （15）

wt = wh + wl1 + 3s = wl1 + wl2 + wl3 + 4s（16）

式中：a1为磁芯边柱的长度；a2为磁芯中柱的长度；b为磁芯的宽度；wh1、wl1、wl2、wl3分别为直流阻抗为Rh1、Rl1、Rl2、Rl3的线圈宽度；s为导线间距和导线与磁芯的间距，为简便运算，s取15 mil（1 mil = 25.4 μm）；wt代表磁芯窗口长度。由式（14）—（16）可以得到Rdch、Rdcl与wh1、wl1、wl2、wl3、h之间的关系。

在2.1节中，针对不同频率下不同厚度PCB线圈的直流阻抗与交流阻抗之间的关系FRh和FRl，可以得到高低频线圈的交流阻抗与直流阻抗之间满足式（17）：

Rach = FRh·RdchRacl = FRl·Rdcl（17）

2.3 PIM损耗的计算及优化

首先针对PIM的第1层线圈进行优化，再推广至整个磁件，式（18）为PIM第1层线圈的总损耗P1。

P1 = Ihrms2Rh + Ilrms2Rl（18）

式中：Ihrms为高频单元电感的有效值；Ilrms为低频单元电感的有效值；Rh为高频线圈的总阻抗；Rl为低频线圈的总阻抗。

将式（10）—（17）代入到式（18）中，可以得到P1的表达式为：

P1 = f1（wh1，wl1，wl2，wl3，h）（19）

为了能够得到低损耗的PIM绕组，将在不同的wh1、wl1、wl2、wl3、h中找到P1的最小值，结合式（16），可得到P1与wl1、wl2满足式（20），在同一h下遍历wl1与wl2，得到其P1的值：

P1 = f2（（wt - 3s - wl1），wl1，wl2，（wt - 4s - wl2），h） （20）

式中：在wl1、wl2取[2.5，3.0] mm下的P1的值如图10所示（其中铜导线h取 70 μm）。

为防止PCB导线中走过电流过大，按工业标准，1 mm铜线承载的最大连续电流为3 A，综合磁芯结构，wh1、wl1、wl2、wl3应当满足式（21）的约束条件：

wh1，wl1，wl2，wl3 gt; 2.5 mmwh1 + wl1 + 3s lt; wtwl1 + wl2 + wl3 + 4s lt; wt（21）

图11为不同铜厚线圈的PIM绕组损耗情况。

从图11中可以看出，70 μm厚的铜箔下绕组的损耗已经较小，虽然105 μm和140 μm厚的铜箔下的绕组损耗更低，但却增加了PCB的成本和工程难度，因此选用70 μm的铜箔作为PIM的绕组，此时高低频线圈的总损耗见图11。

2.4 磁芯损耗

在低损耗的绕组基础上，本节将针对磁芯损耗进行分析。式（22）为任意波形激励下磁芯损耗的计算公式：

Pc_sin = Cf？琢 Bmax？茁VePc_pul = C′K？琢-1Pc_sinK = C′ = （）？琢-1 + （）？琢-1 （22）

式中：Pc_sin为正弦波激励下的磁芯损耗；Pc_pul为任意波形激励下的磁芯损耗； f为正弦波激励的磁密；Bmax为磁件的最大磁通密度；Ve为磁芯体积；C、α、β与磁芯的材料有关；C′、K为中间变量。

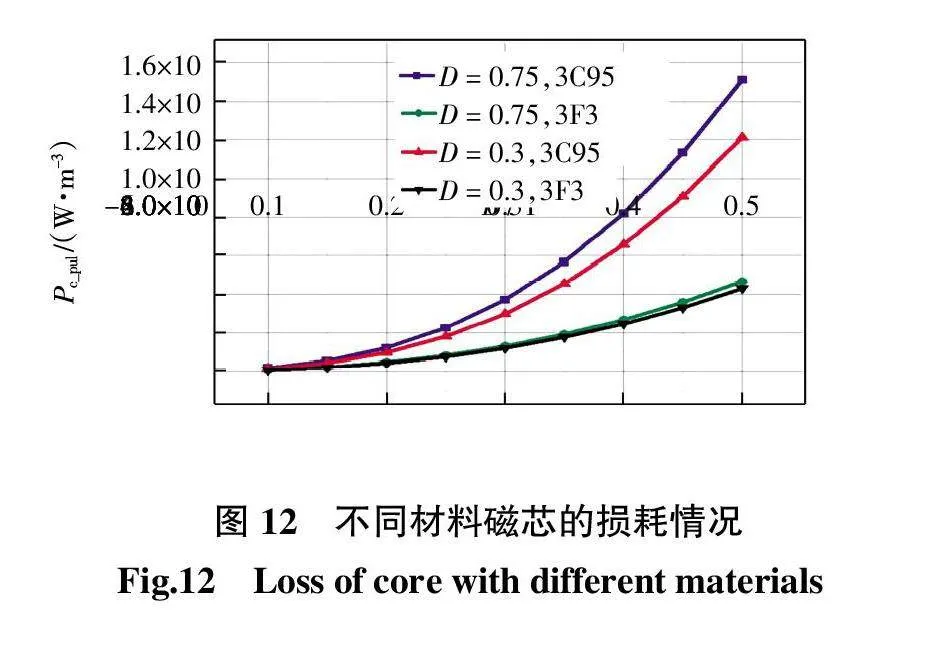
双频变换器的磁芯尺寸将由系统参数决定，磁元件的材料和工作频率成为影响磁芯损耗的重要因素。图12为单位体积不同磁性材料的磁元件激励频率为400 kHz下磁芯损耗情况。

由图12可知，3F3材料的磁芯在此频率段将提供更加优越的性能。

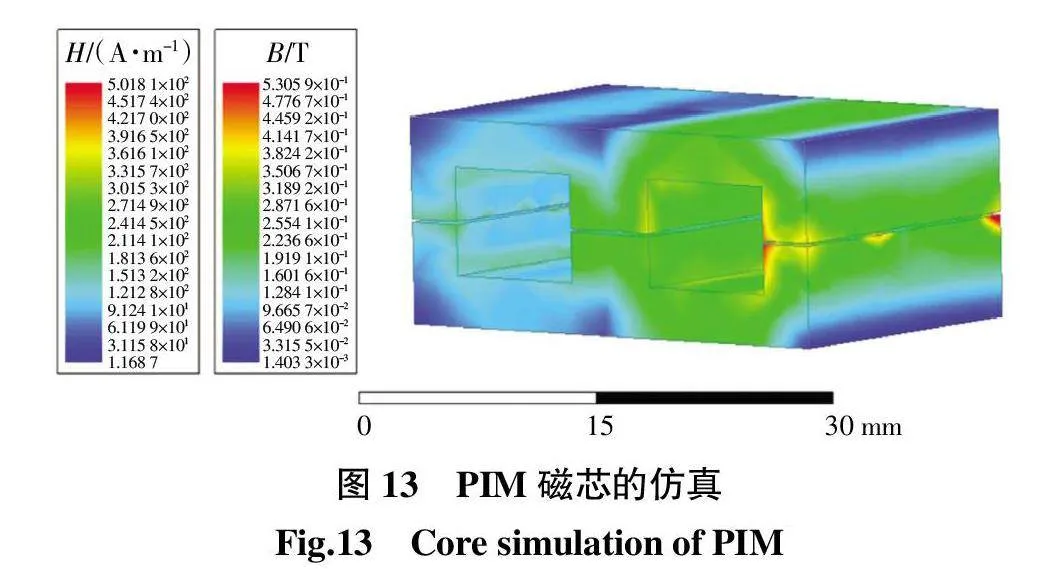
磁性元件在系统中运行时，磁元件的损耗会受到多种因素影响，采用有限元法可以准确分析磁元件损耗，验证磁元件设计正确性。图13为PIM磁芯的磁通密度情况。

通过仿真结果可知，本文设计的磁元件满足系统要求，同时得到磁元件的磁芯损耗。

3 实验验证

图14为本文的DFBuck变换器。

系统的功率器件采用SiC器件，包含优化设计后的平面磁件。为降低系统成本，平面电感器绕组使用3个两层板叠放而成。高频部分工作频率为400 kHz，低频部分工作频率为57.142 kHz。系统的主控制器均采用TI公司的TMS-320F28335。功率器件采用CREE公司的C3M0015065D。对于平面集成电感器，高频电感同低频电感的2个绕组距离不同使得高频电感同低频电感2个绕组耦合系数与理论有所差异，在实际设计时，需通过数字电桥进行测试，并微调磁芯中柱宽度，使得高低频电感完全解耦。

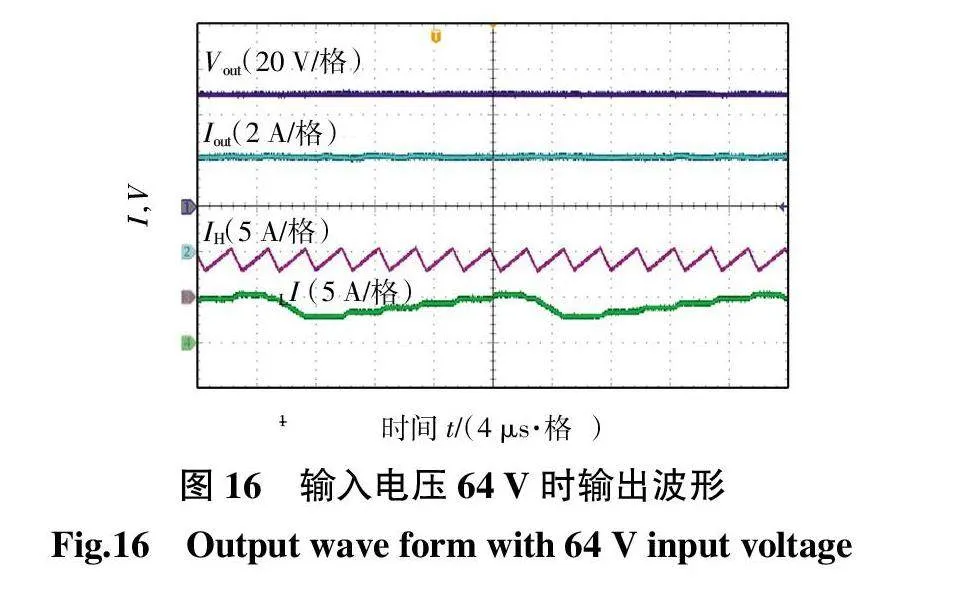
图15和图16分别为输入160 V、64 V电压下系统输出电压Vout、输出电流Iout以及高低频电感电流IH和IL的满载稳态波形。

由图15和图16的实验波形可知，输入电压不同时，系统可保证稳定输出。DFBuck变换器的低频单元与高频单元完全解耦，并且低频单元电流很好地追踪了高频单元电流，符合DFBuck变换器低频单元为高频单元分流的特性。实验波形与理论波形的差异是由于系统效率未达到100%所致。

图17和图18分别为输入160 V、64 V电压下输出电压Vout、输出电流Iout以及高低频电感电流的响应速度曲线。

由图17和图18的实验波形可知，2个输入电压等级下，当负载跳变时，系统均能实现快速响应。图19为传统设计方法下的DFBuck变换器。图19中，功率等级、电压等级与本文样机一致，样机采用Si器件，磁元件采用绕制集成磁件。Si样机参数规格与本文样机参数规格如表1所示。

经测量和计算，SiC样机功率密度将达到46.1 W/in3（1 in = 25.4 mm），远超Si器件样机的10.15 W/in3。图20 比较了 Si 器件系统和 SiC 器件系统的开关损耗和磁性元件损耗。

由图20可见，相较于传统绕制磁件的Si样机，带有平面磁件的SiC样机将造成更低的损耗。针对Si器件的双频Buck变换器与SiC器件的双频Buck变换器全负载范围下系统的效率进行了测试，两系统的测试条件相同，系统效率曲线如图21所示。

由图21可见，输入电压Vin的增加将加大变换器的开关损耗，系统的效率会随着输入电压的降低而升高。由图21还可以看出，本文带有SiC器件的高频DFBuck变换器在全负载范围内均能够高效地完成能量转换，并且能量转换效率优于Si器件的DFBuck变换器。

4 结束语

本文设计了一种高效高功率密度的DFBuck变换器。为了提高变换器的效率与功率密度，系统高频单元定为400 kHz，并使用SiC器件作为功率器件；双频变换器只承担低频单元开关损耗的特性能够减小功率器件的热应力，提高系统效率。电感电流纹波系数的增加将减小变换器磁元件的损耗，有助于有限PCB内的平面电感器的设计；与传统理念不同，带有平面集成磁件的DFBuck变换器系统参数将由平面集成电感器以及双频变换器特性共同决定，这将平衡系统磁元件和开关器件的损耗。针对带有不同频率绕组的平面集成电感器，提出了一种考虑集肤效应和邻近效应的优化方法，并完成DFBuck变换器平面集成电感器的优化设计。最终，完成带有平面集成磁件和SiC器件的高频DFBuck变换器，系统峰值效率为96.1%，功率密度将达到46.1 W/in3，较同等级的低频率样机均得到提高，达到了高效高功率密度的目的。

参考文献：

[1]" " FU M F， FEI C， YANG Y C， et al. A GaN-based DC-DC mo-dule for railway applications： Design consideration and high-frequency digital control[J]. IEEE Transactions on Industrial Electronics， 2020， 67（2）： 1638-1647.

[2]" " DU X， ZHOU L W， TAI H M. Double-frequency buck conve-rter[J]. IEEE Transactions on Industrial Electronics， 2009， 56（5）： 1690-1698.

[3]" " 周雒维， 杜雄， 付志红， 等. 双频Buck变换器[J]. 中国电机工程学报， 2006， 26（6）： 68-72.

ZHOU L W， DU X， FU Z H， et al. The buck converter with double frequency[J]. Proceedings of the CSEE， 2006， 26（6）： 68-72 （in Chinese）.

[4]" " OUYANG Z W， ANDERSEN M A E. Overview of planar mag-netic technology：Fundamental properties[J]. IEEE Transacti-ons on Power Electronics， 2014， 29（9）： 4888-4900.

[5]" " 杜雄， 周雒维， 罗全明， 等. 双频Buck变换器参数对系统性能的影响[J]. 电工技术学报， 2005， 20（11）： 4-10.

DU X， ZHOU L W， LUO Q M， et al. Relationship between circuit parameter and system performance of buck converter with double frequency[J]. Transactions of China Electrotechni-cal Society， 2005， 20（11）： 4-10 （in Chinese）.

[6]" " 张晓峰， 周雒维， 罗全明， 等. 磁集成双频DC/DC变换器[J]. 电工技术学报， 2010， 25（1）：77-83， 89.

ZHANG X F， ZHOU L W， LUO Q M， et al. Double frequency DC/DC converter with magnetic integration[J]. Transactions of China Electrotechnical Society， 2010， 25（1）： 77-83， 89（in Chinese）.

[7]" " GAO S W， WANG H. A new approach integrated magnetics double-frequency DC/DC converter[J]. IEEE Access， 2020， 8： 148301-148314.

[8]" " AHMED M H， LEE F C， LI Q. LLC converter with integrated magnetics application for 48V rack architecture in future data centers[C]//2019 IEEE Conference on Power Electronics and Renewable Energy（CPERE）." Egypt， Aswan： IEEE， 2020： 437-443.

[9]" " AHMED M， FEI C， LEE F C， et al. High-efficiency high-power-density 48/1V sigma converter voltage regulator module[C]//2017 IEEE Applied Power Electronics Conference and Exposition（APEC）. Tampa， FL， USA：IEEE， 2017： 2207-2212.

[10]" LUAN S K， WU Z H， WANG Z W， et al. A high power densi-ty two-stage GaN-based isolated Bi-directional DC-DC con-verter[C]//2019 IEEE Energy Conversion Congress and Exposi-tion（ECCE）. Baltimore， MD， USA：IEEE， 2019： 3240-3244.

[11]" 肖龙， 伍梁， 李新， 等. 高频LLC变换器平面磁集成矩阵变压器的优化设计[J]. 电工技术学报， 2020， 35（4）：758-766.

XIAO L， WU L， LI X， et al. Optimal design of planar magnet-ic integrated matrix transformer for high frequency LLC conve-rter[J]. Transactions of China Electrotechnical Society， 2020， 35（4）：758-766（in Chinese）.

[12]" MU M K， LEE F C. Design and optimization of a 380～12 V high-frequency， high-current LLC converter with GaN devi-ces and planar matrix transformers[J]. IEEE Journal of Emerg-ing and Selected Topics in Power Electronics， 2016， 4（3）： 854-862.

[13]" FEI C， LEE F C， LI Q. High-efficiency high-power-density LLC converter with an integrated planar matrix transformer for high-output current applications[J]. IEEE Transactions on In-dustrial Electronics， 2017， 64（11）： 9072-9082.

[14]" COVE S R， ORDONEZ M， LUCHINO F， et al. Applying re-sponse surface methodology to small planar transformer wind-ing design[J]. IEEE Transactions on Industrial Electronics， 2013， 60（2）： 483-493.

[15]" GUAN Y S， WANG Y J， XU D G， et al. A 1 MHz half-bridge resonant DC/DC converter based on GaN FETs and planar magnetics[J]. IEEE Transactions on Power Electronics， 2017， 32（4）： 2876-2891.

[16]" FU M F， FEI C， YANG Y C， et al. Optimal design of planar magnetic components for a two-stage GaN-based DC-DC con-verter[J]. IEEE Transactions on Power Electronics， 2019， 34（4）： 3329-3338.

[17]" WANG Y F， CHEN B， HOU Y Q， et al. Analysis and design of a 1 MHz bidirectional multi-CLLC resonant DC-DC con-verter with GaN devices[J]. IEEE Transactions on Industrial Electronics， 2020， 67（2）： 1425-1434.

[18]" HURLEY W G， GATH E， BRESLIN J G. Optimizing the AC resistance of multilayer transformer windings with arbitrary current waveforms[J]. IEEE Transactions on Power Electronics， 2000， 15（2）： 369-376.

[19]" NGUYEN M H， FORTIN BLANCHETTE H. Optimizing AC resi-stance of solid PCB winding[J]. Electronics， 2020， 9（5）： 875.

本文引文格式：

高圣伟，于冠恒，赵虹宇. 高频双频Buck变换器平面集成磁件优化设计[J]. 天津工业大学学报，" 2024，" 43（6）： 66-74.

GAO S W， YU G H， ZHAO H Y. Optimal design of planar integrated magnetics for high-frequency double-frequency Buck converter[J]. Journal of Tiangong University，" 2024，" 43（3）： 66-74（in Chinese）.