有效利用易错题微课提升高中数学教学效率

苏华丹

［摘 要］高中数学易错题的错误类型主要包括概念理解不清、公式理解记忆不清楚、审题不清、运算失误、思维不严谨五大方面，如果不及时纠正错误，将会影响学生对数学知识的整体掌握，甚至会影响他们的学业成绩。因此，针对易错题，采取有效的教学方法，提升教学效率非常重要。微课作为一种新兴的教学方式，以其短小精悍、内容丰富、灵活方便、可反复使用等特点备受教育界关注。借助微课，教师可以有针对性地讲解易错题的解题方法和技巧，帮助学生更好地理解和掌握知识点。文章主要探讨如何利用易错题微课提升高中数学教学效率， 为高中数学教师提供参考。

［关键词］易错题微课；高中数学；教学效率

［中图分类号］    G633.6        ［文献标识码］    A        ［文章编号］    1674-6058（2024）14-0017-04

随着新课程改革的不断深入以及社会的持续发展，信息技术给教育教学的发展带来了深刻的变化。信息技术改变了教师的教学方式和学生的学习方式。微课作为一种重要的数字化教学资源，以短小精悍、指向明确、内容丰富、灵活方便、可反复使用等特点，被广泛应用于教育领域[1]。高中数学知识具有高度抽象、知识容量大、思维层次向理性跃迁等特点[2]，习题训练对于巩固知识、规范方法、培养能力以及发展思维至关重要[3]。易错题作为一类典型习题，可以帮助学生诊断知识薄弱点和思维误区，具有巨大的应用价值[4]。借助易错题微课辅助高中数学教学，可以避免“题海战术”，提高学生的错题管理能力，使学生养成良好的学习习惯，同时可以提升高中数学教学效率。

一、高中数学易错题的错误类型

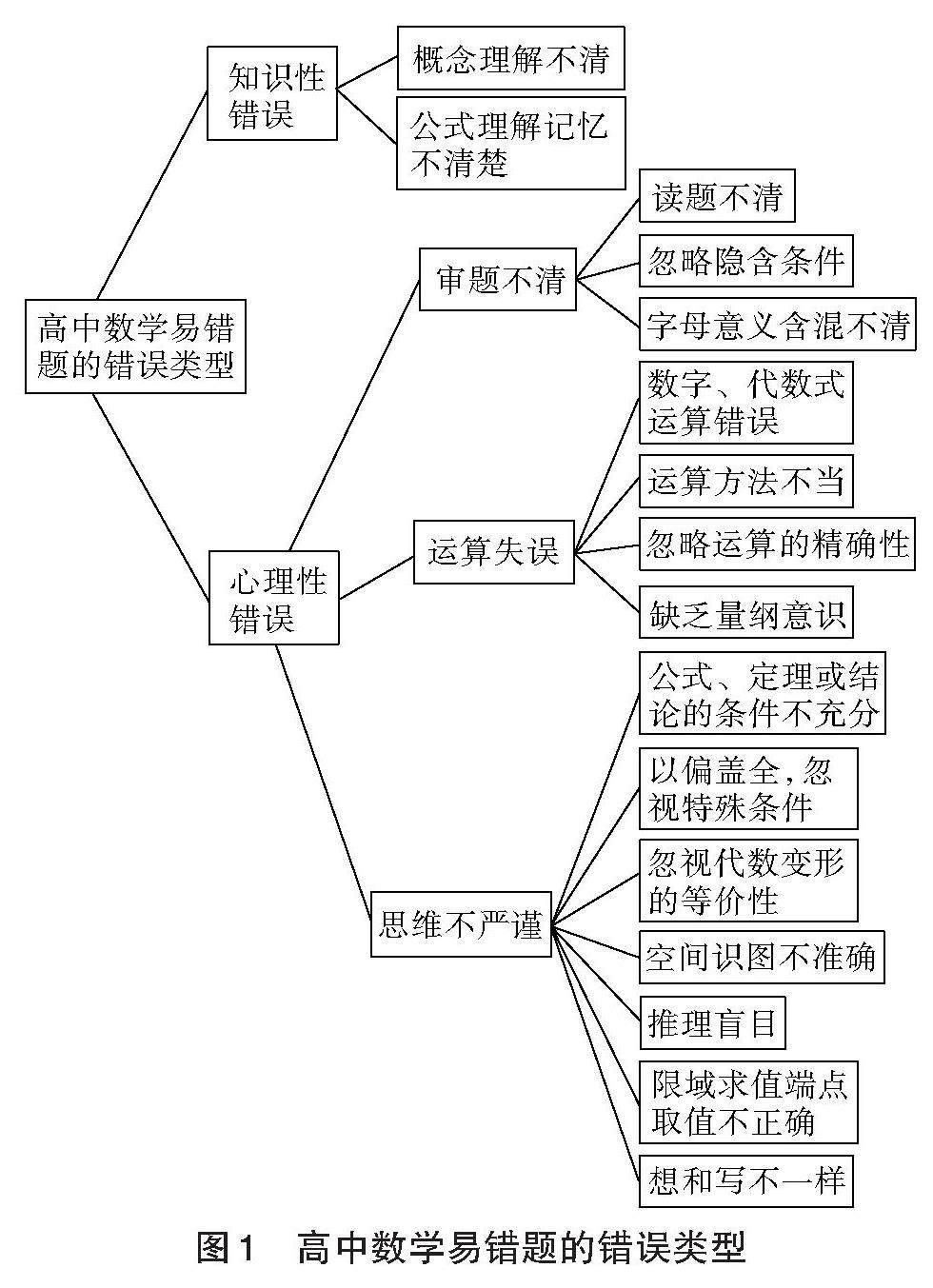
高中数学易错题的错误类型主要包括概念理解不清、公式理解记忆不清楚、审题不严、运算失误、思维不严谨五大方面[5]，如图1所示。概念理解不清，即对概念的理解存在模糊、不完整或者错误的情况，导致无法准确应用相关概念，出现解题错误。公式理解记忆不清楚，即对公式的符号、变量理解记忆不清楚，或者对公式的推导过程或应用情境不清楚，导致错用公式。审题不清，即在解题时没有仔细阅读题目，导致对题目的要求和条件理解不准确，从而影响解题。运算失误，即在计算过程中出现疏忽或错误，导致解题出错。思维不严谨，即在解题时思维不严谨，导致在推理和证明过程中出现错误或遗漏。

二、利用易错题微课提升高中数学教学效率的策略

（一）利用概念型易错题微课，深化学生对基础概念的理解

数学概念是指数学学科中的基本概念或原理，它们是数学体系的基石。概念型易错题微课是一种引导学生对容易出错的基础概念进行深化理解的微课形式。概念型易错题微课通过向学生讲解特定的基础概念，并结合学生容易出错的题目进行解析，帮助学生纠正错误，加深对基础概念的理解。当学生在平时的学习中对数学概念的本质理解不透彻时，就会在解题的过程中反映出来。针对容易出错的概念题，设计概念型微课辅助讲解，可以深化学生对基础概念的理解。

例如，等比数列的概念中要求[a1]和q均不为0，但学生在解题过程中常常忽视该条件，对此教师可以将相关易错题制作成概念型易错题微课，并结合微课进行讲解。

概念型易错题微课的呈现形式如下：

［易错题1］[x=ab]是a、x、b成等比数列的  （）。

A.充要条件

B.充分非必要条件

C.必要非充分条件

D.既不是充分条件又不是必要条件

考查要求：理解等比数列的概念。

错误解答：当[x=ab]时，a、x、b成等比数列成立。同时，当a、x、b成等比数列时，[x=ab]成立，所以[x=ab]为a、x、b成等比数列的充要条件，答案为A。

错因分析：对等比数列的概念理解不清。

正确解析：当[x=a=0]时，[x=ab]成立，但a、x、b不能构成等比数列，因此充分性不成立。反之，当a、x、b成等比数列时，有[x2=ab?x=±ab]，所以[x=ab]不一定能够成立，必要性也不成立。因此，既不是充分条件又不是必要条件，答案为D。

［变式］设a、b、c、d是非零实数，则“[ad=bc]”是“a、b、c、d成等比数列”的（）。

A.充要条件

B.充分非必要条件

C.必要非充分条件

D.既不是充分条件又不是必要条件

通过概念型易错题微课，学生可以针对自己容易出错的题目和概念进行有针对性的训练和学习，从而加深对基础概念的理解，提高解题能力和学习效果。同时，概念型易错题微课也可以激发学生的学习兴趣，促使学生对问题进行深入思考。

（二）利用公式型易错题微课，帮助学生理解记忆公式

公式型易错题微课是指针对特定公式的易错题进行讲解和指导的短小课程，旨在帮助学生理解和掌握特定公式的运用方法和技巧。通过公式型易错题微课，学生可以更好地理解公式的运用方法，避免常见错误，并提高解题的准确性和效率。例如，在运用公式[a+b≥2ab]时，条件有“[a>0]，[b>0]，当且仅当[a=b]时等号成立”，但部分学生会忽视[a]、[b]取值均为正值和取等号的条件，还有学生将一些常用公式记为“[x2=x]”“[1x<1?x>1]”错误公式等。

公式型易错题微课的呈现形式如下：

［易错题2］若[x>0，y>0，x+y=1]，则[1x+4y]的最小值为（）。

A. 7             B. 8             C. 9             D. 10

考查要求：能够对不等式公式进行应用。

错误解答：[1x+4y≥24xy≥41x+y22=8]，因此答案为B。

错因分析：忽略了公式取等号的条件。

正确解析：因为[x+y=1]，所以有[1x+4y=x+yx+4（x+y）y=5+yx+4xy≥9]，所以答案为C。

［变式］函数[y=x+1x+1]（[x≥0]）的最小值为         。

公式型易错题微课帮助学生厘清了数学公式的易错点，使学生能够真正理解和记忆数学公式。借用公式型易错题微课，结合具体实例，对数学公式中的易错点进行分析，可以使学生深刻理解和牢固掌握知识，提高学习效果。

（三）利用审题型易错题微课，让学生学会审题

审题是指在解题前仔细阅读题目，理解题目要求，明确解题思路和方法。学会审题对于解题非常重要，审题是解题的第一步，只有正确理解题目要求，才能准确地解题。常见的审题不清问题有读题不清、忽视隐含条件、字母意义含混不清，教师可选取典型例题，通过微课的形式分别进行讲解。

一是读题不清，即没有仔细阅读题目或者理解题目的要求，导致在解题时出现错误或者偏离题目要求。这种情况包括遗漏题目中的关键信息、误解题目的意思、错误理解题目的要求等。读题不清是学生在审题过程中常见的问题之一，也是影响解题准确性和效率的重要因素。

［易错题3］已知f（x）是R上的奇函数，且当[x>0]时，[f（x）=12x+1]，则[f（x）]的反函数的图象大致为（）。

在解答该题时，学生很容易忽略题干中“反函数”的要求，依据函数[y=12x]在[x>0]的区间递减以及[f（x）]过点（0，2），错误选择B选项。但题干实际要求的是“反函数”，所以正确的求解为：根据函数与其反函数的性质，原函数的定义域与值域同其反函数的值域、定义域相同，原函数中[x>0]，[0<12x<1]，[10]，故选A。

二是忽视隐含条件。忽视隐含条件指的是在解题过程中忽略了问题中未明确陈述但对问题解决具有重要影响的条件。这些条件可能并不是直接给出的，但对于问题的解决却是至关重要的。例如在函数问题中忽视了定义域的限制；在一元二次方程求解中忽视判别式[Δ≥0]的情况等。

［易错题4］设[α、β]是一元二次方程[x2-2kx+k+6=0]的两个实根，求[（α-1）2+（β-1）2]的最小值（）。

A. 7        B. 8         C. [-494]        D.不存在

在求解此题时，学生容易忽视判别式[Δ≥0]的情况，所以会出现如下错解：依据一元二次方程根与系数的关系可得[α+β=2k]，[αβ=k+6]，所以[（α-1）2+（β-1）2=α2-2α+1+β2-2β+1=（α+β）2-2αβ-2（α+β）+2=4k-342-494]，因此最小值为[-494]，答案为C。正确解析：依据一元二次方程根与系数的关系可得[α+β=2k]，[αβ=k+6]，所以[（α-1）2+（β-1）2=α2-2α+1+β2-2β+1=（α+β）2-2αβ-2（α+β）+2=4k-342-494]。因为[α、β]是一元二次方程[x2-2kx+k+6=0]的两个实根，所以[Δ=4k2-4（k+6）≥0?k≤-2]或者[k≥3]。当[k≤-2]时，[（α-1）2+（β-1）2]的最小值为18；当[k≥3]，[（α-1）2+（β-1）2]的最小值为8。

三是字母意义含混不清。在高中数学中，字母通常被用作代表未知数或变量的符号。如果字母的意义含混不清，就会导致解题错误。例如，如果一个问题中使用了多个字母代表不同的变量，但没有说明清楚它们的意义，学生可能会混淆，导致解题出错。另外，有时候字母的意义可能会根据上下文发生变化，如果学生没有正确理解上下文，就可能会误解字母的意义，从而导致解题出错。

（四）利用运算型易错题微课，让学生充分体会计算的重要性

运算能力是指在进行数学运算时所表现出来的能力，包括对数字进行基本的加减乘除等数学运算的能力，对代数式进行变形、化简的能力，以及在运算过程中灵活调整方法、克服困难和纠正错误的能力。运算能力是思维能力和运算技能的有机结合，是应用数学知识解决实际问题的重要基础。引入运算型易错题微课的目的是帮助学生提高运算能力。通过运算型易错题微课，学生可以在短时间内集中学习和练习特定的运算技能，更深入地理解运算规则和方法，从而减少运算错误的发生。

运算型易错题微课的呈现形式如下：

［易错题5］若[a=（5，-7）]，[b=（-1，2）]，且有[（a+λb）⊥b]，则实数[λ]的值为（）。

A. 3              B. [195]              C. 9              D. 10

考查要求：掌握代数式的相关运算方法，例如移项、合并同类项、因式分解等整式变形，繁分式化简，无理式变形等。

错误解答：根据题意可知，[a+λb=（5-λ]，[-7+2λ）]，所以有[（a+λb）⊥b→（a+λb）·b=0→5-λ+2（-7+2λ）=0]，解得[λ=3]，因此答案为A。

错因分析：在上述的计算过程中，数字的运算出错，忽略了[（5-λ）×（-1）]时的符号，两者相乘仍为[5-λ]，导致最终的计算结果出现错误。

正确解析：因为[a+λb=（5-λ，-7+2λ）]，所以有[（a+λb）⊥b→（a+λb）·b=0→λ-5+2（-7+2λ）=0]，求得[λ=195]，所以答案为B。

［变式］已知向量[a=（1，2）]，[b=（2，-2）]，[c=（1，λ）]，若[c]∥[（2a+b）]，则[λ=]         。

（五）利用思维型易错题微课，培养学生的解题思维

数学思维是指在解决数学问题时所表现出来的思考方式和能力。当面对复杂的数学问题情境时，学生很容易因为思维不严谨而导致解题出错，例如以偏概全，重视一般性解题而忽略特殊情况。

思维型易错题微课的呈现形式如下：

［易错题6］数列[an]的前[n]项和为[Sn=n2-2n+3]，则[an=]                 。

考查要求：分类讨论求解数列。

错误解答：根据题意，可以有[an=Sn-Sn-1=（n2-2n+3）-（n-1）2-2（n-1）+3=2n-3]。

错因分析：忽视[n=1]的情况。

正确解析：根据题意，可以有当[n≥2]时，[an=Sn-Sn-1=（n2-2n+3）-（n-1）2-2（n-1）+3=2n-3]，而[a1=S1=2]不适合上式，∴[an=2，n=1，2n-3，n≥2。]

［变式］[Sn]为数列[an]的前[n]项和，若[an>0]，[an2+2an=4Sn+3]，则[an]=               。

新高考改革突出知识为基、能力为重，坚持素养导向和价值引领。在新高考背景下，教师利用微课讲解易错题这一新教学模式，打破了传统的数学教学模式，使得学生“学习习惯不良与错题重要性认识不足”和教师“授课进度紧张与错题讲解效率低下”等问题得到了有效解决，不仅帮助学生改善了学习习惯，使学生能够自主思考和主动学习，还强化教师对学生易错题的教学管理，提高了教师的教学效率。

［   参   考   文   献   ］

[1]  张家文.利用微课提高高中数学习题课教学的有效性[J].数理天地（高中版），2023（13）：89-91.

[2]  朱云飞，蔡薇.微课背景下的高中数学错题管理策略探析[J]. 理科考试研究，2023（9）：29-31.

[3]  黄燕.高中数学复合函数习题教学探究[J].中学教学参考，2021（2）：8-9.

[4]  史宇宙.高中数学课堂利用易错题提升教学质量的建议[J].新智慧，2017（31）：21.

[5]  沈宏.高中数学易错题的分类与成因分析[J].中学数学月刊，2015（12）：54-56.

（责任编辑    黄春香）

［基金项目］南宁市教育科学“十四五”规划2021年度“高中数学易错题AR化应用研究”课题（立项编号：2021C127）。