一类特殊矩阵中2矩阵与其和矩阵特征向量关系
2024-07-07刘海涛朱宇航
刘海涛 朱宇航
摘 要: 在有干扰的条件下,为从具有正弦波特征的采样数据求取一次谐波系数,设计了滤波程序。通过对干扰误差对谐波系数影响机理的分析,得到了一个特殊的由三角函数值构成的二阶矩阵,矩阵的特征值和特征向量决定了计算效率,两个干扰对应两个子矩阵,其和矩阵与子矩阵的特征值及特征向量构成了有趣的关系。一类特殊的,当自变量分别为α和β,构成2个矩阵,其和矩阵的特征向量与这2个矩阵的特征向量呈现出简单的函数关系。为动平衡机干扰信号的消除提供了数学基础。
关键词: 矩阵和特征值 特征向量 滤波 谐波系数
中图分类号: TP18文献标识码: A文章编号: 1679-3567(2024)04-0082-04
Relationship Between Matrix 2 and Its Sum Matrix Eigenvectors in a Special Type of Matrix
LIU Haitao1 ZHU Yuhang2
1.Weihai Guangtai Airport Equipment Co., Ltd., Weihai, Shandong Province, 264200 China; 2.CAM Ve‐hicle Testing Engineering Research Institute of China, Beijing, 102100 China
Abstract: In the presence of interference, we designed a filtering program to obtain the first harmonic coefficient from sampled data with sine wave characteristics. By analyzing the impact mechanism of interference errors on harmonic coefficients, a special second-order matrix composed of trigonometric function values was obtained. The eigenvalues and eigenvectors of the matrix determine computational efficiency. Two interferences correspond to two sub matrices, and the eigenvalues and eigenvectors of its sum matrix and sub matrices form interesting relationship In a special type of matrix, when independent variables are α and β respectively, two matrices are formed, the eigenvectors of its sum matrix show simple functional relationship with the eigenvectors of the two matrices, which provides a mathematical basis for eliminating the interference signals of dynamic balancing machines.
Key Words: Matrix and Eigenvalues; Eigenvector; Filtering; Harmonic coefficient
动平衡机传感器的输出是正弦函数的采样值,只有一次谐波,若发生干扰,将导致谐波系数产生偏差,而动平衡机最终输出的动不平衡量,是完全依赖谐波系数计算得出的[1],一些针对正弦波的低通滤波方法[2-3]包括巴特沃斯滤波器[4-5]仅使数据平滑,并不能在数学上保证数据的准确。由于动平衡机旋转一周得到的大量采样数据只计算出一次谐波系数这两个数值,数据冗余量大且干扰均为脉冲类的窄干扰,针对此特点,笔者设计了可保证精度的滤波方法。做迭代运算,先求出在干扰条件下的谐波系数,用此具有误差的谐波系数生成正弦波,覆盖掉干扰区间的采样数据,得到下一个级次的谐波系数,直至两次相邻迭代的谐波系数足够接近为止。此方法理论上可达到任意精度。迭代运算主要是矩阵计算,与计算矩阵特征值和特征向量的乘幂法[6]相似,较好地解决了脉冲干扰问题。本文分析了双脉冲迭代矩阵的特征值和特征向量,为滤波软件的设计提供了数学基础。
1 矩阵的来源

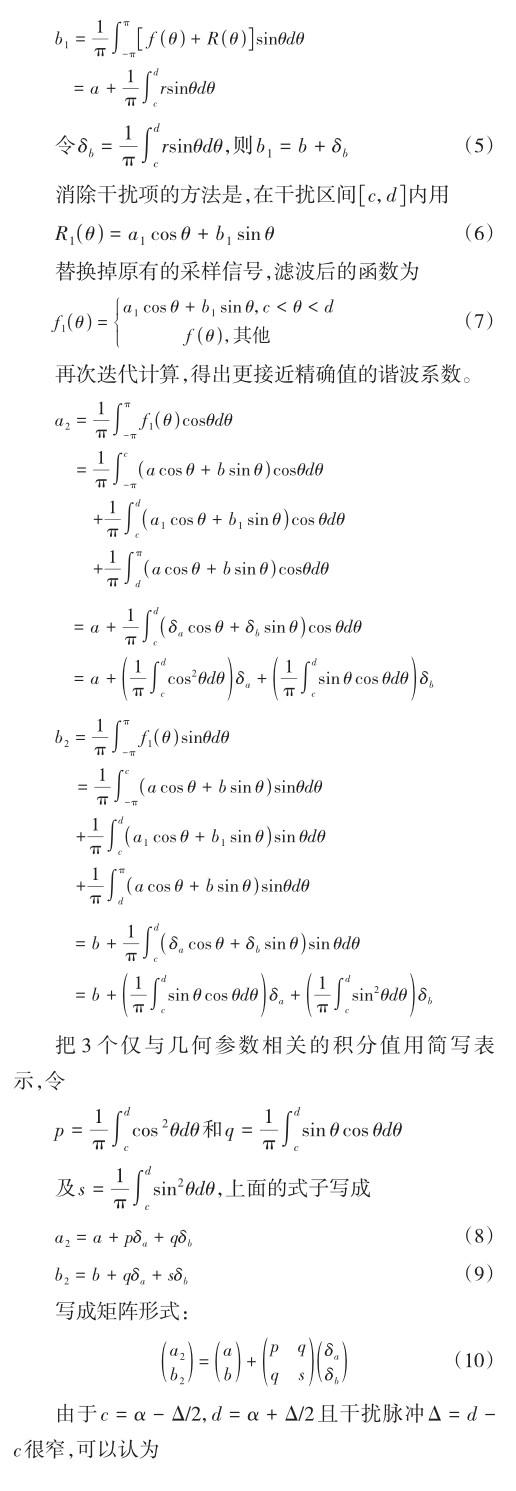


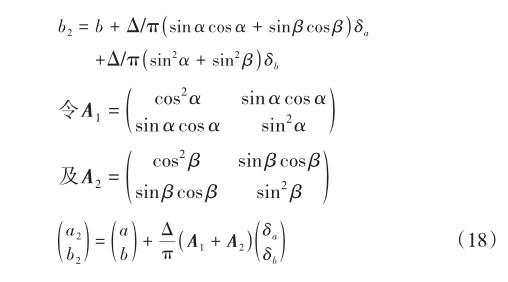
2 特征值和特征向量的计算


其和矩阵特征向量自变量为构成和矩阵的2个矩阵特征向量对应三角函数自变量的算数平均值,这是一个有趣的结果。
3 结语
笔者曾用本文方法对动平衡机传感器进行信号分析,根据傅里叶级数的特点,提出了一种基于矩阵迭代计算的滤波方法,通过对迭代过程矩阵特征值和特征向量的分析,为迭代算法和加速算法的设计提供了数学基础。实验表明:滤波后得到的谐波系数确实具有数学精度,加速算法的设计使得迭代的收敛速度满足了现场的要求。本文方法为正弦波类信号的滤波提供了一种选择。
参考文献
[1]朱宇航,史云鹏.动平衡的力学分析及算法[J].建筑工程技术与设计,2020(19):359-361.
[2]侯鹏飞,杨跃文,徐海东.一种单相系统参考电流检测改进算法[J].电工技术,2022(5):44-47,53.
[3]宋潇.一种变积分时间谐波检测算法[J].现代电子技术,2022,45(23):144-148.
[4]杨辉.巴特沃斯低通滤波器的设计与仿真分析[J].电子产品世界,2022,29(12):79-81.
[5]黄波.巴特沃斯数字滤波器的设计与仿真实现[J].河南科技,2021,40(36):10-12.
[6]曹志浩,张玉德,李瑞遐编.矩阵计算和方程求根[M].北京:高等教育出版社,1979:123.
[7]何旭初,苏煜城,包雪松.计算数学简明教程[M].北京:高等教育出版社,1980:229.
