某座椅鞭打试验仿真与优化

王元兰　赵军　毛晨曦　刘会霞

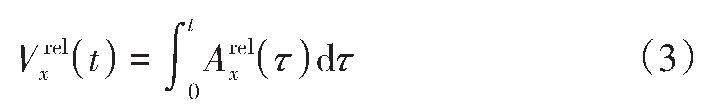
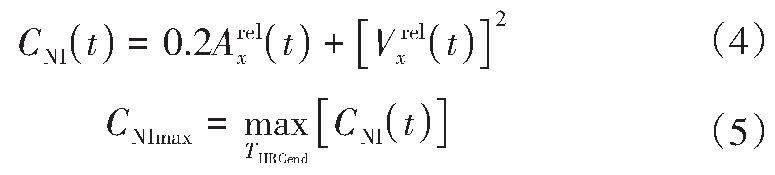
【摘要】针对某款座椅在鞭打试验中假人挥鞭伤较为严重，鞭打得分较低的问题，利用HyperMesh软件建立座椅有限元模型，并进行鞭打仿真分析，得到对鞭打伤害影响较大的因素分别为调角器刚度系数、头枕杆直径、靠背左侧支撑板厚度、靠背右侧支撑板厚度、靠背后部支撑板厚度、座垫右侧支撑板厚度和座垫左侧支撑板厚度，利用哈默斯雷试验设计方法对上述7个设计变量进行样本点采集，并利用移动最小二乘法进行近似模型拟合，采用全局响应面法对近似模型进行多目标优化，验证结果表明，优化模型的精度满足要求，优化后鞭打得分提高，座椅抗挥鞭伤性能显著提升。

主题词：座椅 鞭打试验 挥鞭伤 中国新车评价规程 多目标优化

中图分类号：U463.836   文献标识码：A   DOI： 10.19620/j.cnki.1000-3703.20230589

Simulation and Optimization of A Seat Whipping Test

【Abstract】The results of whiplash test show that whiplash injury is very serious and whiplash score is low. To solve this problem， the seat finite element model was established by HyperMesh software， and the whipping simulation analysis was carried out. The factors affecting substantially whipping injury were analyzed as follows： angle adjuster stiffness coefficient， head pillow rod diameter， thickness of backrest left support plate， thickness of backrest right support plate， thickness of backrest rear support plate， thickness of seat cushion left support plate and thickness of seat cushion right support plate. The above seven influencing factors were taken as design variables， sample points were collected by Hammersley experimental design， and approximate model fitting was carried out by moving least square method. The global response surface method was used to perform multi-objective optimization of the approximate model. The verification results show that the accuracy of the optimized model meets the requirements， and the whip score was increased， which greatly enhanced the seats ability to prevent whip injury.

Key words： Seat， Whiplash test， Whiplash injury， C-NCAP， Multi-objective optimization

1 前言

车辆低速追尾事故极易带来乘员的颅脑损伤、颈椎损伤、心脏损伤等伤害[1]，各国研究人员非常重视座椅抗挥鞭伤性能研究，2012年，座椅鞭打试验纳入中国新车评价规程（China-New Car Assessment Program，C-NCAP）[2]。

目前，座椅安全性能的主流研究方法有2种[3]，即台车碰撞试验和计算机数值模拟。经过数十年的发展，有限元法已经大量应用于座椅被动安全开发领域[4-5]：刘迪辉[6]对车辆追尾过程中乘员颈部的运动状态和损伤机理进行了研究；赵民等[7]按照GB 11550—2009《汽车座椅头枕强度要求和试验方法》对某款汽车的座椅头枕进行了静强度仿真验证；李瑞生[8]基于C-NCAP座椅鞭打试验要求研究发现，座椅的抗挥鞭伤性能受靠背刚度、头枕刚度和安装位置等多种因素影响；张程[9]基于挥鞭伤试验研究发现某座椅失分原因为头枕结构设计不合理，并通过结构优化提高了座椅抗挥鞭伤性能。我国对座椅安全性能的研究逐渐成熟。

本文按照2021年版《C-NCAP管理规则》的要求安排鞭打试验，对试验结果进行分析，利用HyperMesh软件构建鞭打试验的CAE模型，并利用LS-DYNA求解器计算有限元模型，与鞭打试验结果进行对比分析来验证有限元模型的可靠性，然后根据仿真结果分析对座椅抗挥鞭伤性能影响较大的因素，并将其作为设计变量进行试验设计，以试验设计采集的数据为基础搭建近似模型，最后基于近似模型进行多目标优化，以提高座椅抗挥鞭伤性能。

2 鞭打试验及结果分析

2.1 鞭打试验

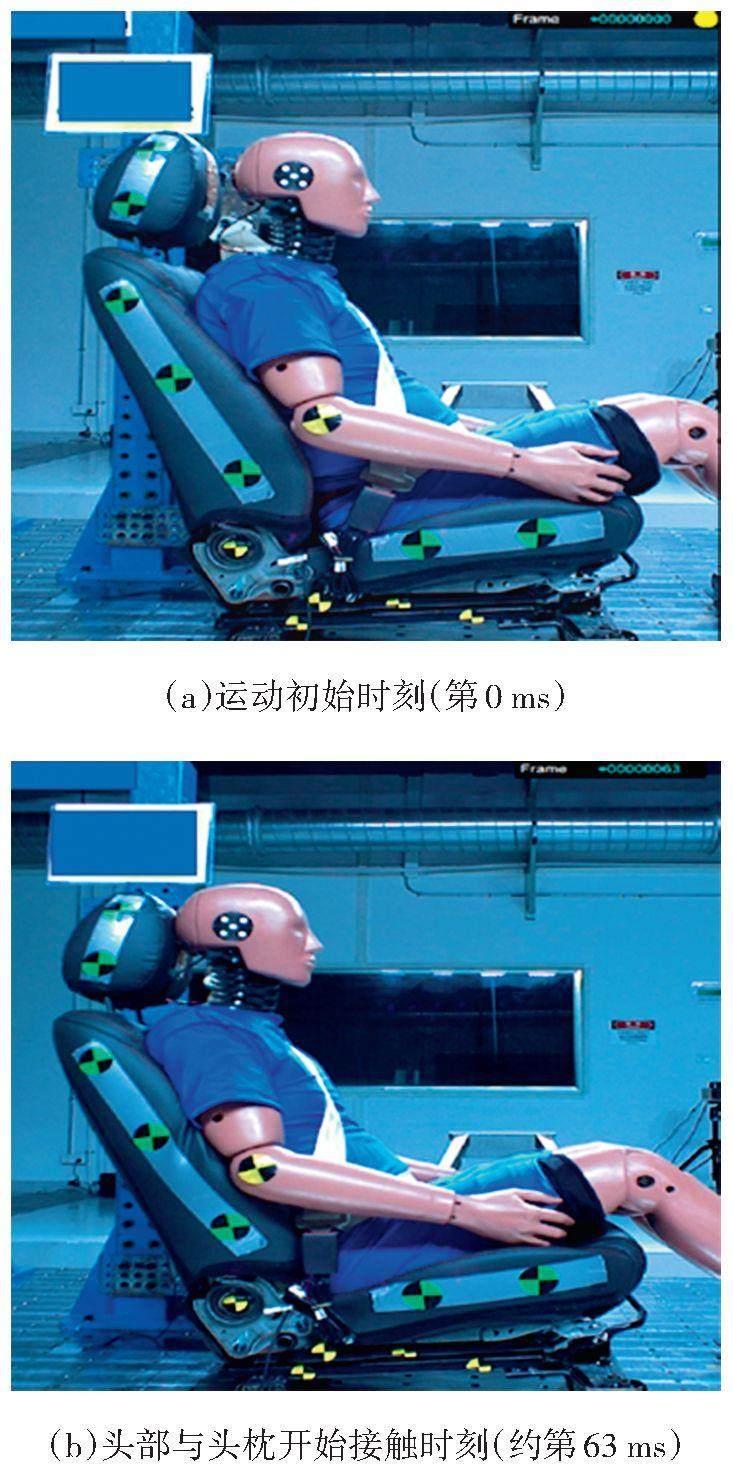
根据C-NCAP鞭打试验动态规程[10]，鞭打试验需要在温度为22.5 ℃、相对湿度为10%～70%的环境条件下进行，试验前，假人和座椅需在该环境中静置至少3 h。在试验过程中，至少需要2台帧速率为1 000 帧/s的高速摄像机，其中一台用于拍摄假人与座椅的整体运动状态，另一台用于拍摄座椅头枕与假人头部的运动状态，记录时间均为第0～300 ms。完成上述试验准备后向试验台车加载特定加速度。动态试验完成后，查看高速摄像机记录的鞭打试验视频，关键帧如图1所示。

2.2 鞭打试验结果分析

提取假人搭载的传感器记录的数据，如图2所示，由图2可以看出，上颈部剪切力与拉力的最大值分别为约207 N和约546 N，下颈部剪切力与拉力的最大值分别为约462 N和约836 N，上、下颈部扭矩最大值的绝对值分别为约35 N·m和约5 N·m，颈部伤害指数（Neck Injury Criterion，NIC）的最大值为15.54 m2/s2。

根据上述结果和2021年版《C-NCAP管理规则》中的鞭打评分准则进行评分，结果如表1所示。

由表1可知，本次鞭打试验NIC得分率为65.5%，上颈部得分率为14.7%，下颈部得分率为52.7%，总体得分率为46.4%，座椅抗挥鞭伤能力有很大的优化空间。本文采用有限元分析再设计的方式进一步优化座椅设计参数，从而减少座椅试验次数、缩短研发周期。

3 鞭打CAE模型搭建与试验对比分析

3.1 CAE模型及工况搭建

将座椅几何模型导入HyperMesh进行有限元网格划分，设置合理的连接方式、接触方式及材料属性等；接着将假人合理安装在座椅上，并调整假人与座椅的初始干涉，如图3所示。以鞭打试验波形作为输入载荷提交计算，如图4所示。

3.2 对比分析

提取有限元计算结果，并将其伤害曲线与试验伤害曲线进行对比，以验证有限元模型的精度，结果如图5所示。

由图5可知，鞭打仿真伤害曲线与试验伤害曲线整体趋势接近，拟合程度较高，因此该有限元模型可用于后续的优化设计。

4 伤害分析与优化

4.1 提出设计变量

由表1可知，NIC、上颈部扭矩及下颈部拉力得分均不高。NIC可以反映颈椎的整体伤害程度，通过比较枕骨关节与胸部之间的水平加速度差和速度差来确定。

相对加速度为：

[Arelxt=AT1xt-AHeadxt]                          （1）

其中：

相对速度为：

式中：[AT1xt]为胸部（第一胸椎，T1）加速度；[AHeadxt]为枕骨加速度，即头部加速度；[AT1-Leftxt]、[AT1-Rightxt]分别为左、右侧胸部加速度。

颈部伤害指数为：

式中：THRCend为头部与头枕接触后的分离时刻，CNImax为颈部伤害指数最大值。

由式（4）可知，颈部伤害指数由头部与胸部的加速度差和速度差决定，其中速度由加速度积分获得，因此NIC可简化为由头部与胸部的加速度差决定，故减小头部与胸部的加速度差即可减小NIC。

分析座椅结构与人体结构可知，对乘员胸部与头部加速度差影响较大的因素包括调角器刚度系数、头枕杆直径、靠背左侧支撑板厚度、靠背右侧支撑板厚度、靠背后部支撑板厚度、座垫右侧支撑板厚度和座垫左侧支撑板厚度。以上述7个影响因素作为设计变量，取值范围如表2所示。

4.2 试验设计方法选择与样本点采集

哈默斯雷试验设计[11]法在设计变量较多、采样空间较广泛时，能够以较少的采样点反映整个设计空间的特性，且其在采样点的空间分布均匀性方面优于拉丁超立方采样，因此本文选择哈默斯雷试验设计方法。

任意整数a均可用基数B表示为[12]：

a=a0+a1B+a2B2+…+anBn                       （6）

式中：a0～an均为0～9范围内的整数，n为样本点数量：

[n]的计算公式为：

[n=logBa]                                  （7）

0～1之间的任意唯一小数φB（a）（反基数）可表示为：

φB（a）=a0B-1+a1B-2+…+anB-n-1                 （8）

k维随机分布的M个采样点集合Pk（a）可表达为：

式中：Pk（a）为采样点集合，M为样本数量，a=1，2，…，M，B1，B2，…，Bk-1为（k-1）项素数。

则生成的M个k维哈默斯雷序列点集合Xk（a）可表示为：

Xk（a）=1-Pk（a）                        （10）

在进行哈默斯雷试验设计时，须对试验次数进行估计。与拉丁超立方采样类似，若需获得一个二阶多项式，则至少需进行（v+1）（v+2）/2次试验，推荐试验次数为（v+1）（v+2）次，其中m为设计变量数量，本文的设计变量共有7个，按照推荐次数计算，需进行72次试验，设计变量采样数据如表3所示，其中V1为调角器刚度系数，V2～V7分别为头枕杆直径、靠背左侧支撑板厚度、靠背右侧支撑板厚度、靠背后部支撑板厚度、座垫右侧支撑板厚度、座垫左侧支撑板厚度。

4.3 近似模型建立及精度分析

本文采用移动最小二乘法建立近似模型，构建一个由系数向量a（x）和基函数p（x）构成的拟合函数[13]，设待求函数f（x）在拟合求解区域Ω中的N个采样点xI（I=1，2，…，N）处的函数值uI=u（xI）已知，移动最小二乘法的目的是在Ω中构造待求函数f（x）的全局近似函数fa（x），待求函数f（x）在点x的局部域Ωx内可局部近似为：

移动最小二乘法拟合曲面的基本思想是先将待拟合的区域离散化，然后利用公式求解出网格上的节点值，最后连接各网格节点形成拟合曲面[14]，设计流程如图6所示。

基于试验设计采集的样本点，采用上述移动最小二乘法的公式拟合近似模型，同时需对得到的近似模型精度进行验证。

近似模型可以通过确定系数R2来评价其拟合精度[15]，R2在0.800～0.995范围内时，表示拟合精度很好：

本文近似模型的精度如表4所示，其中R1～R7分别为上颈部剪切力、上颈部拉力、上颈部弯矩、下颈部剪切力、下颈部拉力、下颈部弯矩、NIC。

由表4可知，各响应的近似模型精度均大于0.9，因此近似模型的精度很好，可以用于后续优化。

4.4 基于近似模型的多目标优化

多目标优化（Multi-Objective Optimization，MOO）是优化目标多于1个的优化问题，可以描述为：

式中：f（x）为目标函数，x为决策向量，u为优化目标的数量，gi（x）为第i个约束不等式，hj（x）为第j个约束等式，fu（x）为第u个优化目标，D为设计变量集合域，xd为设计变量，xd_min、xd_max为可行域边界。

本文采用全局响应面法（Global Response Surface Method，GRSM）进行多目标优化，其框架如图7所示。第1轮迭代结束，GRSM会根据第1次迭代的样本点数据自动拟合响应面。GRSM可基于非常少的数据点生成响应面，对于具有大规模设计变量的问题仍保持很高的计算效率。

选用全局响应面法对座椅骨架进行多目标优化，以上颈部拉力、上颈部剪切力、上颈部弯矩、下颈部剪切力、下颈部拉力、下颈部弯矩最小，以及颈部伤害指数最小为目标函数，进行多目标优化设计，其数学表达式为：

优化过程中设置最大迭代次数为200次，经过97次迭代运算完成整个优化过程，由上述分析可知，鞭打仿真过程中NIC、上颈部弯矩和下颈部拉力失分较为严重，且颈部伤害指数在C-NCAP评分中占比较高。颈部伤害指数对上颈部弯矩和下颈部拉力的帕累托（Pareto）前沿如图8所示。

从图8中可以看出：随着颈部伤害指数的增大，上颈部弯矩整体呈下降趋势；颈部伤害指数与下颈部拉力分布集中在中部，在下颈部拉力最小时，颈部伤害指数不会达到最大或最小值。故需根据C-NCAP中各项指标的评分占比来选择一组最优解，本文选取第42次迭代中的第2 089组解作为最终优化结果，优化后的设计变量如表5所示。

4.5 优化结果分析验证

为了验证优化结果的有效性，需要将选取的设计变量的优化值代入有限元模型中进行分析，并将计算结果与基于近似模型优化得到的结果进行对比，结果如表6所示。

由表6可知，仿真结果与近似值之间存在一定误差，但均未超过8%，因此优化结果具有参考价值。

将优化后的仿真结果代入鞭打损伤评分规则，并对比优化前、后的鞭打得分情况，如表7所示。由表7可知，经过优化，鞭打总分从2.14分提升到3.35分。

由上述分析可知，仿真结果与近似模型的结果误差较小，鞭打损伤评分和座椅的抗挥鞭伤性能大幅提升。

5 结束语

本文针对碰撞过程中假人颈部伤害较大的问题，提出了一种座椅抗挥鞭伤性能优化方法，建立座椅鞭打有限元模型并验证了其精度与可靠性，分析并提出了7个对鞭打损伤影响较大的因素，采用哈默斯雷试验设计法对7个设计变量进行样本点采集，并用移动最小二乘法建立各响应的近似模型，通过对各响应确定系数R2的判断，验证了所建立的近似模型具有较高的精度。采用全局响应面法对所建立的近似模型进行优化，得到了各响应的最优设计方案，根据分析结果提出了一组最优解并验证了优化结果的精度。最后，根据C-NCAP鞭打损伤评分规则进行评分，结果表明，优化后座椅的抗挥鞭伤性能大幅提升。

参 考 文 献

[1] KUMAGAI G， WADA K， TANAKA S， et al. Prevalence of Whiplash Injury and Its Association with Quality of Life in Local Residents in Japan： A Cross Sectional Study[J].      Journal of Orthopaedic Science， 2022， 27（1）： 108-114.

[2] 张楚云. 汽车座椅鞭打试验综述[J]. 内燃机与配件， 2021（14）： 198-199.

ZHANG C Y. Overview of Automotive Seat Whiplash Test[J]. Internal Combustion Engine and Accessories， 2021（14）： 198-199.

[3] COLASANTI E. Design and Development of a Lightweight Seat Frame Using Magnesium Extrusions and Stampings[J]. SAE Technical Papers， 940406， 1994.

[4] WILSON H. Structural Feasibility of Injection Molded and Compression Molded Front Seat Bases[J]. SAE Technical   Papers， 920496， 1992.

[5] 马健胜， 郭树文， 郑艳婷， 等. 基于某SUV正碰台车试验的有限元建模仿真研究[J]. 天津科技， 2019， 46（3）： 54-59+62.

MA J S， GUO S W， ZHENG Y T， et al. Research on Finite Element Modeling Simulation Based on an SUV Frontal    Impact Sled Test[J]. Tianjin Science and Technology， 2019， 46（3）： 54-59+62.

[6] 刘迪辉. 汽车追尾事故中乘员颈部的冲击生物力学响应和损伤机理研究[D]. 长沙： 湖南大学， 2002.

LIU D H. Research on Impact Biomechanical Response and Injury Mechanism of Occupant's Neck in Automobile Rear End Collision[D]. Changsha： Hunan University， 2002.

[7] 赵民， 孙晶， 王宇， 等. 某汽车座椅头枕静强度仿真分析与优化[J]. 机械设计与制造， 2020（8）： 73-75+79.

ZHAO M SUN J， WANG Y， et al. Simulation Analysis and Optimization of Static Strength of a Certain Car Seat Headrest[J]. Mechanical Design and Manufacturing， 2020（8）： 73-75+79.

[8] 李瑞生. 某汽车座椅鞭打性能的研究与优化[D]. 长春： 吉林大学， 2016.

LI R S. Research and Optimization of Whipping               Performance of a Car Seat[D]. Changchun： Jilin University， 2016.

[9] 张程. 汽车座椅挥鞭伤性能要求及提升方案[J]. 汽车工程师， 2021（1）： 51-54.

ZHANG C. Whiplash Performance Requirements and       Improvement Scheme of Car Seat[J]. Automotive Engineer， 2021（1）： 51-54.

[10] 中国汽车技术研究中心有限公司. C-NCAP管理规则（2021年版）[S]. 天津： 中国汽车技术研究中心有限公司， 2021.

China Automotive Technology Research Center Co.， Ltd.. C-NCAP Management Rules （2021 Edition）[S]. Tianjin： China Automotive Technology Research Center Co.， Ltd.， 2021.

[11] 何映平. 试验设计与分析[M]. 北京： 化学工业出版社， 2013.

HE Y P. Design of Experiments and Analysis[M]. Beijing： Chemical Industry Press， 2013.

[12] 邓利军， 王书贤， 杨芳庆. 汽车前防撞梁的耐撞性与轻量化优化设计[J]. 现代制造工程， 2021（8）： 64-69.

DENG L J， WANG S X， YANG F Q. Crash Resistance and Lightweight Optimization Design of Automotive Front    Bumper Beams[J]. Modern Manufacturing Engineering， 2021（8）： 64-69.

[13] 张勇. 基于近似模型的汽车轻量化优化设计方法[D]. 长沙： 湖南大学， 2009.

ZHANG Y. Optimization Design Method of Vehicle      Lightweight Based on Approximate Model[D]. Changsha： Hunan University， 2009.

[14] 曾清红， 卢德唐. 基于移动最小二乘法的曲线曲面拟合[J]. 工程图学学报， 2004（1）： 84-89.

ZENG Q H， LU D T. Curve and Surface Fitting Based on Moving Least Squares[J]. Journal of Engineering Drawing， 2004（1）： 84-89.

[15] 苏绍娟， 刘灿波， 张祥， 等. 基于RBF代理模型的NOBS油船货舱结构多目标优化设计[J]. 武汉理工大学学报， 2021， 43（11）： 35-42.

SU S J， LIU C B， ZHANG X， et al. Multi Objective          Optimization Design of Cargo Tank Structure of NOBS Oil Tanker Based on RBF Surrogate Model[J]. Journal of      Wuhan University of Technology， 2021， 43（11）： 35-42.