基于二次转角约束的改进RRT路径规划算法研究

鲍家定 钟国安 马果 徐海军 景晖

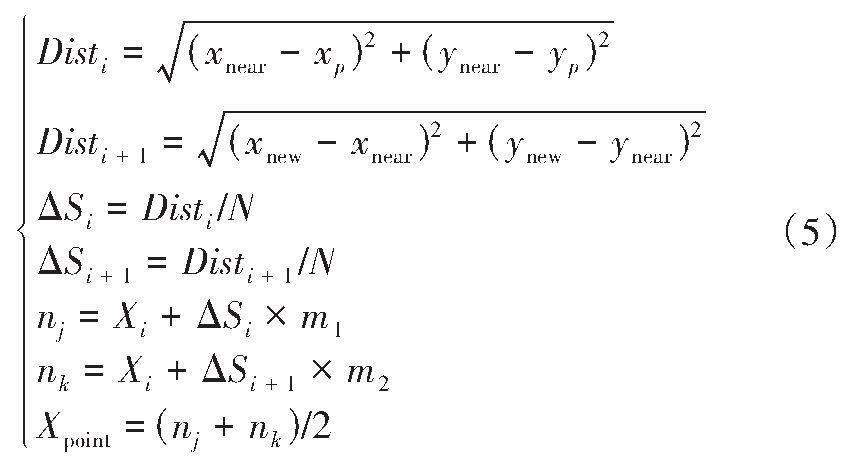
【摘要】针对快速随机搜索树（RRT）算法存在节点扩展冗余、生成路径不满足车辆转角条件等问题，提出一种改进的二次转角约束RRT算法。首先，在传统RRT算法基础上对采样空间进行裁剪，引入目标导向策略减少采样时间；然后采用车辆膨胀处理和直线方法检测障碍物，并引入第一次转角约束得到粗解路径；接着对粗解路径建立二次转角约束并进行优化处理，获取优化路径后拟合，并进行仿真验证。结果表明，相比于引入目标导向策略的RRT算法，所提出的算法路径最大曲率降低了34.33%，平均曲率降低47.36%，扩展节点数降低47.62%，路径距离降低7.76%，规划时间缩短14.98%。

主题词：改进RRT算法 转向角度约束 路径规划 路径曲率 路径平滑性

中图分类号：U461.99   文献标志码：A   DOI： 10.19620/j.cnki.1000-3703.20230371

Research on Improved RRT Path Planning Algorithm Based on Two-Time Steer Angel Constraint

【Abstract】Aiming at the problems that the Rapid-exploration Random Tree （RRT） algorithm is easy to lead to node expansion redundancy and the generated path does not meet the vehicle rotation angle constraint， an improved secondary rotation angle constraint RRT algorithm is proposed. Based on the traditional RRT algorithm， the sampling space is first cut， and the target offset strategy is introduced to reduce the sampling time. Then， the vehicle expansion processing and the straight line method are used to detect the obstacle collision， and the first rotation angle constraint is introduced to obtain the coarse solution path. Then， the secondary angle constraint optimization processing is established for the rough solution path， and the vehicle optimization path is obtained and fitted， and the simulation verification is carried out. The results show that compared with the biased RRT algorithm with the goal-oriented strategy， the maximum curvature of the path is reduced by 34.33 %， the average curvature is reduced by 47.36 %， the number of extended nodes is reduced by 47.62 %， the path distance is reduced by 7.76 %， and the planning time is reduced by 14.98 %.

Key words： Improved RRT algorithm， Steering angle constrain， Path planning， Path curvature， Path smoothness

1 前言

路径规划技术作为无人驾驶汽车实现自主导航的关键技术之一，对车辆安全行驶起着至关重要的作用，逐渐成为无人驾驶车辆领域研究热点[1-2]。

路径规划算法可分为基于图搜索的算法（如A*算法、Dijkstra算法等）、基于随机采样的算法（如快速随机搜索树（Rapid-exploration Random Tree，RRT）算法、蒙特卡洛随机采样算法等），以及深度学习算法、蚁群算法等[3-7]。

RRT算法作为一种常用的路径规划算法，通过随机采样状态空间生成新节点，并不断扩展树形结构，搜索可行路径，具有较强的灵活性。栾添添等[8]提出了一种动态变采样区域RRT路径规划算法，减少了节点的采样次数并降低了搜索的盲目性。Zhang等[9]利用人工势场法，对采样目标进行启发式引导，再根据障碍物密度动态调整步长，提出了动态步长RRT算法。Chen等[10]为了解决RRT算法搜索效率低的问题，提出了一种改进的RRT连接路径规划（Improved Rapid-exploration Random Tree-Connect）算法。Ghosh等[11]在不影响精度的情况下限制生成的节点数量，并结合动力学约束生成平滑的轨迹，提出了一种基于运动学约束的双向RRT（Kinematically Constrained Bidirectional-RRT）算法。许万等[12]针对RRT*全局路径规划算法在多障碍物复杂环境中搜索效率低、占用内存过大、搜索路径不平滑等问题，提出一种基于简化地图的区域采样RRT*算法（Simplified Map-based Regional Sampling RRT*，SMRS-RRT*）。朱冰等[13]针对RRT和RRT*算法存在路径抖动大、易陷入局部区域和计算效率低等缺点，提出了一种基于安全场改进RRT*算法的路径规划方法。Shi等[14]针对RRT算法随机性大、收敛速度慢、易产生偏差的问题，采用循环交替迭代搜索法和双向随机树搜索法对RRT算法进行了改进和优化。Tahir等[15]为了克服复杂环境的算法收敛速度，提出了潜在性引导智能双向RRT*（Potentially Guided Intelligent Bi-directional RRT*）方法。

综上所述，目前RRT算法已提高了算法收敛速度，但仍存在获取路径不平滑、路径曲折及采样点数量过多等问题。为解决上述问题，本文提出基于二次转角约束改进的RRT路径规划算法，通过对采样点进行第一次转角约束获得粗解路径，然后对粗解路径进行第二次转角约束获得优化路径，以此提高路径的平滑性。最后通过仿真试验验证所提出算法的有效性。

2 偏置RRT算法

2.1 基本RRT算法原理

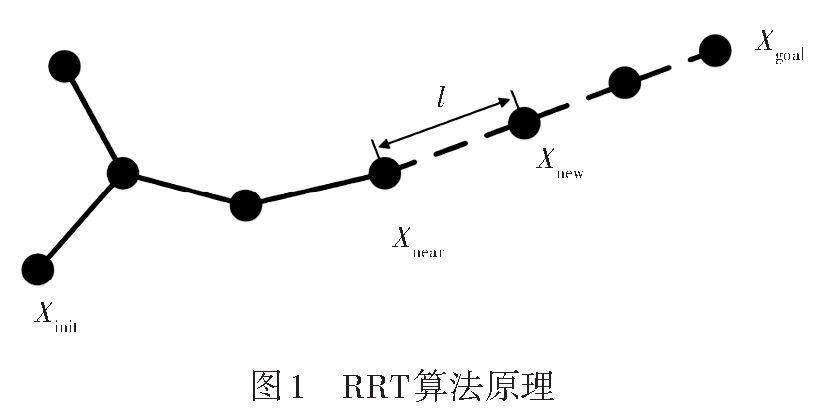
RRT算法是一种基于随机空间采样的路径规划算法，可以直接应用于非完整约束系统的路径规划，且在多维复杂环境中具有极高的搜索效率，算法原理如图1所示。

RRT算法基本流程为：首先确定起始点Xinit和目标点Xgoal，并以Xinit为起点生成扩展随机树Tnode，随后进行状态空间采样；然后在空间中选定一随机点Xrand，以Xrand的最近点Xnear和Xrand的连线为生长方向，若Xnear与Xrand的连线未经过障碍物，则确定Xrand；其次以Xnear和Xrand连线作为扩展方向，设定步长[l]生成一个新的节点Xnew。若Xnear向Xnew方向扩展过程中不与障碍物发生碰撞，则将Xnew放入Tnode中，若发生碰撞，则重新采样随机点。最后重复上述步骤，直到新产生的节点Xnew与目标点Xgoal的距离小于设定阈值时，算法停止，并回溯获取路径。

2.2 目标约束采样

为了降低RRT算法拓展节点的盲目性，使随机树寻找过程更迅速，本文对随机点的选取进行约束。基于概率p对目标节点进行偏置采样，若随机率p产生的概率小于设定偏置概率阈值p1，则在自由空间里进行随机采样，反之，随机点即为目标点Xgoal，偏置采样公式为：

式中：R为随机采样函数获取的采样点。

3 改进的RRT算法原理

为避免RRT算法搜索的盲目性，对其进行偏置导向处理，但偏置RRT算法获取的路径不一定满足车辆转向要求且路径不够平滑。为了获取满足车辆运动参数的行驶路径，针对车辆转向角度及采样点约束对RRT算法路径生成过程进行优化，改进后的RRT算法流程如图2所示。

改进RRT算法路径生成步骤如下：

a. 初始化起始点Xinit、目标点Xgoal，以及第一次转向角度约束值θ1、第二次转向角度约束值θ2和车辆膨胀尺寸R。

b. 空间剪枝以约束采样点的生成。以一定概率p选择目标点为采样点生成Xrand。

c. 选取距离Xrand最近节点Xnear以及Xnear的父节点Xp进行第一次转角约束判断，若满足θ1，则扩展生成Xnew。利用车辆碰撞圆和偏置直线碰撞融合方法检测Xnear与Xrand之间是否存在碰撞。如果不存在碰撞，则连接节点。重复上述步骤，当Xnew与目标节点的距离小于设定值时，获得粗解路径。

d. 为获得平滑的路径，采用等距离散点对粗解路径进行数值优化，计算转向角度差值并进行障碍物碰撞判断，若转向角度均满足θ2，则优化成功。

3.1 目标偏置策略和约束采样

当随机点Xrand产生后，在随机树Tnode寻找与随机点最近的Xnear，同时对两点之间进行障碍物检测。若存在障碍物，则重新生成随机点Xrand；如果两者之间不存在障碍物，在两者连线的方向以步长l进行拓展，得到新节点Xnew：

[Xnew=Xnear+l×[sinαcosα]] （2）

式中：[α]为Xnear与Xrand之间的夹角。

3.2 采样空间约束

为了提高随机点的选取效率，对随机点进行了空间约束处理，如图3所示。Xinit为随机树采样起点，Xgoal为搜索目标点，绿色区域为障碍物，实线为自由空间边界，虚线为空间剪枝后的采样区域，随机点Xrand在虚线区域内获得。

3.3 车辆膨胀及障碍物避障策略

针对扩展节点未考虑车辆真实尺寸导致碰撞障碍物的情况，本文采用车辆碰撞圆和偏置直线融合方法对障碍物进行检测，碰撞检测原理如图4、图5所示。

车辆膨胀圆的计算公式为：

式中：[δ]为松弛因子，[L]为车辆长度，[B]为车宽度，R为车辆膨胀半径。

为使车辆能够更好地避开障碍物，采用偏置直线策略对当前节点Xcur与新生成的节点Xnew连线进行障碍物碰撞逻辑判断，见图5。lleft为左边偏置直线，lright为右边偏置直线，R为车辆膨胀半径，当lleft和lright两条直线都不与障碍物发生碰撞时，表明车辆可以通行。

3.4 二次转角约束

为获取符合车辆转向角度的路径，计算出Xrand、Xrand、Xnew3个点间的航向角度θ，若θ满足θ1约束，获取第一次转向约束的随机点Xrand，然后依据式（2）获得新节点Xnew：

式中：Xp为Xnear的父节点，Xnear为距离Xrand的最近点，[θ]为路径航向角。

通过对Xrand的角度约束，不断生成Xnew，当Xnew与Xgoal的距离小于θ1时，获得第一次转角约束后的粗解路径，如图6所示。在图6a中，θs1满足θ1，其对应的Xrand满足约束，所以扩展该方向节点生成Xnew，否则如图6b所示，θs2未满足约束要求，则不拓展Xnew。

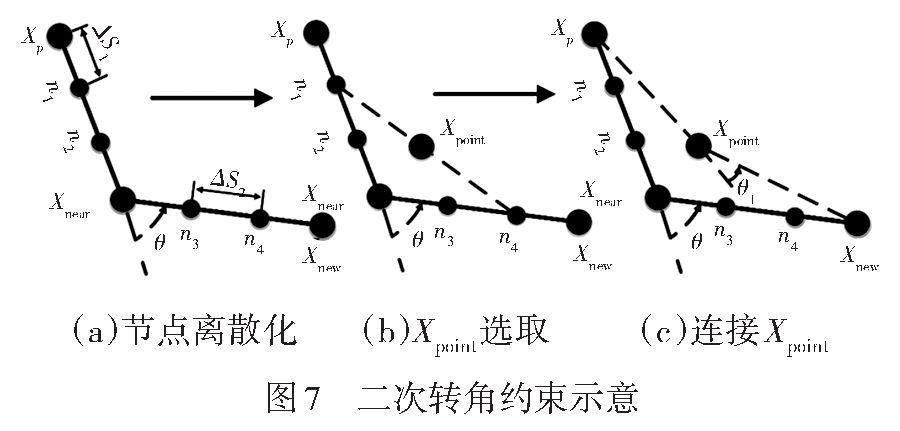
当获得粗解路径时，各个节点之间的曲率以及转向角度并不同时满足要求，可能存在较为尖锐的路径点，为此，本文对粗解路径进行第二次转角约束优化以获取优化路径，如图7所示。

通过对粗解路径当前节点Xnear分别与Xp及Xnew两者之间的连线进行等距离离散化，可分别求得离散点n1、n2、n3、n4，将n3、n4两离散点连接，取两点的平均值，即可得到优化节点Xpoint，通过式（4）计算三点之间的航向角θ，若θ满足二次转向角度约束的阈值θ2范围内，即用Xpoint代替Xnear，重复上述步骤即可得到优化路径，Xpoint选取计算方式为：

式中：i=（1，2，…，n-1）；N为离散点数量；m1、m2分别为第i点与第（i-1）点之间的单位向量及第（i+1）点与第i点之间的单位向量，nj与nk为离散点的坐标信息，其中j=（1，2，…，N），k=（2N，2N-1，…，N）；?Si为Xnear与Xp的均匀离散距离；?Si+1为Xnear与Xnew的均匀离散距离。

3.4 B样条曲线的路径平滑

B样条函数通过插值、逼近和拟合的方式应用于路径平滑处理。

本文采用3次B样条曲线作为路径平滑方法，三阶B样条函数计算如下：

式中：u为自变量，取值范围为[0，1]；i为控制点索引；k为B样条阶数；Pi为第i个控制点；Bi，k（u）为第i个k阶B样条基函数；j为起始的控制点下标索引，相当于控制点从Pj到Pj+k；[Cjk+1=（k+1）！/（j！（k+1-j）！）]。

最终得到3次均匀B样条曲线的基函数表达式为：

将其带入式（6），可得：

4 仿真试验

为了验证所提出算法的有效性，对偏置RRT算法以及改进的RRT算法分别在常规场景Map1、狭窄场景Map2、复杂场景Map3进行20次和30次仿真试验。其中，对随机点Xrand的选取采用90°、75°、60°进行第一次转角约束确定Xnew，生成粗解路径，之后对获取的粗解路径采用20°二次转向角约束获取优化路径，仿真试验参数如表1所示。

4.1 拟合前路径

图8、图9、图10分别Map1、Map2、Map3地图下偏置RRT算法与二次转角约束的改进RRT算法规划路径对比结果。从图中可看出，改进的RRT算法减小了树节点的冗余，减少了无效节点的生成，且改进的RRT算法都能够对障碍物进行避障。从图8a、图9a及图10a可以看出，偏置RRT算法产生的路径节点之间较为曲折，路径不够平滑。图8b、图9b以及图10b中实线为第一次转角约束获取的粗解路径，虚线为第二次转向约束路径的优化路径，由此可以看出，改进的RRT算法大幅度地减小了路径的曲折性，提高了节点之间连接的平滑性。

不同转向角度约束下Map1、Map2、Map3的改进RRT算法粗解路径与优化路径仿真结果分析如图11、图12及图13所示，实线为以90°、75°和60°为第一次转向角度约束获取的粗解路径，虚线为以20°为第二次转向角度约束的优化路径，可以明显看出粗解路径在节点连接某处转向角度过大，路径过于曲折，但当转向角角度逐渐减小时，转角角度约束加强，节点之间的曲折性有所减弱，避免了尖锐节点的产生。

对粗解路径进行约束后获得的优化路径相比于粗解路径，可以明显看出所改进的基于二次转角约束的RRT算法能更好地改善路径节点之间的曲折性，获取路径更加平滑，符合车辆转向要求。

为了更好地验证改进RRT算法的优化效果，对偏置RRT算法及改进的RRT算法得到的仿真结果进行统计，表2所示为第一次转角约束90°、75°和60°，第二次转角约束20°生成的优化路径与偏置RRT算法生成路径的各参数对比。在Map1常规地图中，可看到在不同转角约束条件下，优化路径最大曲率降低43.33%、路径平均曲率降低48.33%、平均扩展节点降低44.59%、平均距离降低8.56%、平均时间降低23.81%；在Map2狭窄地图中，优化路径最大曲率降低38.88%、路径平均曲率降低了48.41%、平均扩展节点降低59.13%、平均距离降低9.59%，但由于Map2的复杂性及空间的狭窄性，可以看到随着第一次转角约束的加强，虽然导致采样节点增多，平均时间逐渐增大，但提高了节点之间的连接平滑性；在Map3复杂地图中，优化路径最大曲率降低39.76%、路径平均曲率降低51.61%、平均扩展节点降低72.59%、平均距离降低11.61%、平均时间降低了72.05%。

由此可知，本文所提出的算法各项指标明显提升，能够在不同角度约束下规划出满足车辆正常行驶的路径，减小道路曲率及路径节点数量，提高路径平滑性。

4.2 B样条曲线拟合路径

采用3次均匀B样条曲线将90°、75°、60°3种转向角度约束下获取得到的粗解路径与优化后的路径进行拟合，验证所提出算法的有效性。

Map1、Map2、Map3拟合的路径如图14～图16所示，其中虚线为粗解路径拟合结果，点线为优化路径拟合结果。分析可知，经过第一次转角约束后，不同场景下拟合的粗解路径仍存在尖锐点，导致路径不够平滑。从图中的3种约束角度对比可知，随着约束角度降低，路径的曲折性相对降低，图14c的粗解拟合路径曲线并未出现更大的曲折点，对比粗解拟合路径和优化拟合后路径可知，优化拟合后的路径在不同的场景都较为平滑，路径的转角角度得到了更好的优化，符合车辆的转角角度约束，减小了路径的曲率，拟合路径更加平滑，验证了所提出算法的有效性。

5 结束语

本文针对传统RRT算法搜索速率慢、节点扩展冗余、路径点不满足车辆转向角度条件及曲率不平滑问题，提出了二次转角约束的改进的RRT算法。基于MATLAB平台搭建了常规地图、狭窄地图和复杂地图，对所提出的改进RRT算法与偏置RRT算法进行仿真分析。仿真结果表明，所提出的改进RRT算法总体上使路径最大曲率降低了34.33%，平均曲率降低了47.36%，扩展节点数降低47.62%，路径距离降低了7.76%，规划时间降低14.98%，拟合后的路径更加平滑，在满足车辆转角的同时，减少了行驶距离，提高了车辆行驶舒适性。

参 考 文 献

[1] TAHA A E， ABUALI N. Route Planning Considerations for Autonomous Vehicles[J]. IEEE Communications Magazine， 2018， 56（10）： 78-84.

[2] BADUE C， GUIDOLINI R， CARNEIRO R V， et al. Self-Driving Cars： A Survey[J]. Expert Systems with Applications， 2021， 165.

[3] GONZ?LEZ D， P?REZ J， MILAN?S V， et al. A Review of Motion Planning Techniques for Automated Vehicles[J]. IEEE Transactions on Intelligent Transportation Systems， 2015， 17（4）： 1135-1145.

[4] LAVALLE S M， KUFFNER J J. Randomized Kinodynamic Planning[J]. The International Journal of Robotics Research， 2001， 20（5）： 378-400.

[5] CHEN C， JIANG J， LV N， et al. An Intelligent Path Planning Scheme of Autonomous Vehicles Platoon Using Deep Reinforcement Learning on Network Edge[J]. IEEE Access， 2020， 8： 99059-99069.

[6] DORIGO M， MANIEZZO V， COLORNI A. Ant System： Optimization by A Colony of Cooperating Agents[J]. IEEE Transactions on Systems， Man， and Cybernetics， Part B （Cybernetics）， 1996， 26（1）： 29-41.

[7] V?RAS L G D O， MEDEIROS F L L， GUIMAR?ES L N F. Systematic Literature Review of Sampling Process in Rapidly-Exploring Random Trees[J]. IEEE Access， 2019， 7： 50933-50953.

[8] 栾添添， 王皓， 孙明晓， 等.基于动态变采样区域RRT的无人车路径规划[J]. 控制与决策， 2023， 38（6）： 1721-1729.

LUAN T T， WANG H， SUN M X， et al. Path Planning of Unmanned Vehicle Based on Dynamic Variable Sampling Area RRT[J]. Control and Decision， 2023， 38（6）： 1721-1729.

[9] ZHANG Y， WANG R， SONG C， et al. An Improved Dynamic Step Size RRT Algorithm in Complex Environments[C]. 2021 33rd Chinese Control and Decision Conference （CCDC）. Kunming， China： IEEE， 2021.

[10] CHEN J， ZHAO Y， XU X. Improved RRT-Connect Based Path Planning Algorithm for Mobile Robots[J]. IEEE Access， 2021， 9： 145988-145999.

[11] GHOSH D， NANDAKUMAR G， NARAYANAN K， et al. Kinematic Constraints Based Bi-Directional RRT （KB-RRT） with Parameterized Trajectories for Robot Path Planning in Cluttered Environment[C]// 2019 International Conference on Robotics and Automation （ICRA）. Montreal， Canada： IEEE， 2019.

[12] 许万， 杨晔， 余磊涛， 等. 一种基于改进RRT*的全局路径规划算法[J]. 控制与决策， 2022， 37（4）： 829-838.

XU W， YANG Y， YU L T， et al. A Global Path Planning Algorithm Based on Improved RRT*[J]. Control and Decision， 2022， 37（4）： 829-838.

[13] 朱冰， 韩嘉懿， 赵健， 等. 基于安全场改进RRT*算法的智能汽车路径规划方法[J]. 汽车工程， 2020， 42（9）： 1145-1150.

ZHU B， HAN J Y， ZHAO J， et al. Safety Field-Based Improved RRT* Algorithm for Path Planning of Intelligent Vehicle[J]. Automotive Engineering， 2020， 42（9）： 1145-1150.

[14] SHI Y， LI Q， BU S， et al. Research on Intelligent Vehicle Path Planning Based on Rapidly-Exploring Random Tree[J]. Mathematical Problems in Engineering， 2020， 2020： 1-14.

[15] TAHIR Z， QURESHI A H， AYAZ Y， et al. Potentially Guided Bidirectionalized RRT* for Fast Optimal Path Planning in Cluttered Environments[J]. Robotics and Autonomous Systems， 2018， 108： 13-27.