基于虚拟电力系统稳定器的低频振荡抑制策略

摘 要：基于虚拟同步发电机（VSG）控制的新能源机组虽可增强电网惯量及频率稳定性，但可能继承与同步机类似的低频振荡问题。针对该问题，首先基于单台VSG并网的线性化模型，构建了适用于VSG的Phillips-Heffron模型，借助阻尼转矩法挖掘了VSG低频振荡的诱发机理。进一步提出一种附加于VSG无功环节的虚拟电力系统稳定器（VPSS），并给出了控制结构及基于相位补偿法的参数设计过程。研究结果表明：VSG发生低频振荡是由于系统受扰后，虚拟功角的振荡信号经过虚拟励磁调节器对VSG机电振荡回路产生了负阻尼转矩。将所提VPSS接入系统可在几乎不影响振荡频率的前提下，实现0.1～3 Hz下VSG低频振荡的有效抑制。

关键词：虚拟同步发电机；虚拟电力系统稳定器；低频振荡；阻尼转矩分析；相位补偿法

DOI：10.15938/j.emc.2024.05.000

中图分类号：TM761文献标志码：A

Low frequency oscillation suppression strategy based on virtual power system stabilizer

[JZ（］WANG Haixin HE Haiwen LIU Mingqi YANG Zihao HAO Yan YANG Junyou CHEN Zhe2

（1.School of Electrical Engineering， Shenyang University of Technology， Shenyang 110870， China;2.Department of Energy Technology， Aalborg University， Aalborg DK-9220， Denmark）

Abstract：Although renewable energy sources controlled by virtual synchronous generator （VSG） could enhance the inertia and frequency stability of the power grid， they may inherit the low-frequency oscillation problem similar to synchronous generator. To address this issue， the Phillips-Heffron model suitable for VSG is constructed at first based on the linearized model of single VSG connected to the grid， and the induction mechanism of low-frequency oscillation of VSG is explored by the damping torque method. Furthermore， a virtual power system stabilizer （VPSS） integrated into the reactive power link of VSG is proposed， and the control structure and parameter design process based on phase compensation method are given. The research results show that low-frequency oscillation of VSG is caused by the negative damping torque of electromechanical oscillation circuit of VSG generated by the oscillation signal of virtual power angle through the virtual excitation regulator after system disturbed. The low-frequency oscillation of VSG at 0.1-3 Hz could be suppressed effectively after VPSS integrated into the system without the oscillation frequency is affected.

Keywords：virtual synchronous generator; virtual power system stabilizer; low-frequency oscillation; damping torque analysis; phase compensation method

0 引 言

随着高比例新能源、高比例电力电子设备接入电力系统的“双高”特征的形成，传统的火力发电逐步由光伏、风电等可再生能源取代，形成以新能源为主体的新型电力系统[1]。这一背景下，为保证电源侧出力的可持续性与充分性，新能源多运行于最大功率跟踪（maximum power point tracking，MPPT）的控制方式。然而，基于MPPT控制的新能源机组几乎无法参与系统调频，使电力系统呈“低惯量”特征，导致电力系统频率稳定性问题加剧，且增大了功率振荡风险[2]。

为克服这一弊端，有学者提出在新能源机组控制回路引入虚拟惯量控制，进而为系统提供惯量支撑[3-4]。其中，因具备类似同步发电机（synchronous generator，SG）的惯量、阻尼支撑能力，虚拟同步发电机（virtual synchronous generator，VSG）受到广泛应用[5]。然而，在机电暂态时间尺度下，VSG会继承SG的小信号稳定性问题，存在一定的低频振荡风险[6]。这是由于VSG转子运动方程的引入导致其虚拟功角变化时，体现出与同步机类似的低频振荡特征，即VSG低频振荡可视为由虚拟功角变化引起的低频功率振荡现象[7-8]。

回顾国内外针对传统低频振荡（仅由SG参与）的相关研究可知，其本质为系统受扰后SG励磁电压调节器向机电振荡回路提供的负阻尼转矩对转子运动（功角）产生不利影响，进而引发低频振荡失稳现象，该振荡信号一般以功率、功角等形式存在，频率在0.1～2.5 Hz之间。针对传统低频振荡的抑制研究，电力系统稳定器（power system stabilizer，PSS）取得了丰富的理论和实践成果，其本质为补偿励磁电压调节器对机电振荡回路产生的负阻尼转矩，在实际工程中多采用基于相位补偿的参数整定方法。然而，目前并未有研究将PSS设计思路应用于由VSG虚拟功角主导的“新型”低频振荡问题，相应的解决方案主要从以下两方面展开研究：

1）第一类是针对VSG低频振荡机理的探索。文献[9]通过构建多VSG参与的交流系统线性化互联模型，发现当VSG子系统与剩余子系统的开环振荡模式相近时，会导致低频振荡更易发生（自谐振机理）。文献[10]运用阻尼转矩法，观察到VSG可向系统中同步发电机的机电振荡回路提供阻尼转矩，进而使系统易于产生低频振荡。文献[11]将虚拟阻尼转矩系数作为计及无功环接入的VSG稳定判据，发现当VSG重载运行或阻抗比较小时，无功-电压环的引入会增大其振荡风险。进一步，文献[12]指出VSG阻尼可分为虚拟转子固有阻尼和等效电磁转矩提供的附加阻尼两部分，其中后者通常为负且受无功环影响较大，文献[13]提出利用李雅普诺夫函数评估系统的稳定运行区域，量化了VSG无功控制回路对系统稳定性的影响。然而，上述研究集中于机理探索和稳定性分析，并没有给出很好的低频振荡抑制方法。

2）第二类是基于VSG的低频振荡抑制研究。文献[14]通过分析振荡模式与转动惯量、阻尼的关系，提出一种转动惯量与阻尼系数自适应控制策略。文献[15]指出平滑调整VSG参数可降低直流电压变化率，以达到抑制低频振荡的目的。然而，参数的实时优化取决于频率变化率及其变化趋势，鲁棒性较差且不易实现。因此，另有学者致力于调整VSG控制结构以提升特定工况下的稳定性。文献[16]将VSG与电网之间的相位偏差进行前馈，以建立新的阻尼功率机制，但对于不同扰动，固定的参数难以达到最优阻尼效果。文献[17]通过在VSG无功环中引入额外的闭环极点，以抑制功角振荡，但该方法增加了系统阶数，不利于系统稳定性的分析。总的来说，上述研究参数选取不易，稍有不慎将恶化系统动态性能，甚至引发低频振荡。

综上所述，为有效抑制VSG参与的“新型”低频振荡，其策略研究多聚焦于参数的实时优化与结构的改变等，但鲁棒性难以保证且失稳风险较大。因此，本文考虑到PSS技术成熟、鲁棒性高且实施性强的特点，提出了一种用于VSG低频振荡抑制的虚拟电力系统稳定器（virtual power system stabilizer，VPSS）策略，主要贡献如下：

1）提出了一种附加VPSS的VSG控制算法改进策略。当电力系统受到不同扰动时，所提控制器可显著提高系统阻尼，减少低频振荡风险，同时对于系统稳定性的改善具有一定的有效性与优越性。

2）构建基于VSG的Phillips-Heffron模型，发现VSG的无功控制（虚拟励磁调节）回路虽可增强系统调压能力，但也对VSG的机电振荡回路造成了负面影响，降低了VSG的稳定性。

1 虚拟同步发电机低频振荡机理

1.1 系统拓扑结构

由于参数灵活可变的特点，VSG动态特性分布于较宽频段。然而，当VSG工作于低频段，且阻尼不足时，易与系统中的同步发电机组低频段开环传递函数极点排斥而致其右移，易于产生低频振荡现象[9]。因此，本文重点关注电力系统机电暂态尺度下由VSG转子运动方程引发的低频段功率振荡问题，忽略中高频段VSG的电压电流环节[12]，VSG接入无穷大电网的系统结构如图1[18]所示。

图1中：ω1、ωg分别为VSG虚拟角频率电网基准频率（标幺值）；Pref、Qref分别为VSG有功和无功设定值；P1、Q1分别为输出有功和无功的计算值；J和Dp分别为VSG的惯性系数和阻尼系数；KQ为无功控制器的增益；V1∠φ和VG∠0°分别对应公共连接点1（point of common coupling 1，PCC1）和PCC2（电网）的电压幅值与相位。对该系统：

1.3 基于阻尼转矩法的VSG低频振荡机理分析

参考同步机功角主导的传统低频振荡负阻尼机理，当VSG无功控制环节向机电振荡回路提供的等效阻尼转矩为负时，易引发由虚拟功角δ1主导的VSG低频振荡模态。为此，本文采用阻尼转矩分析法探究VSG低频振荡的产生机理，通过分析虚拟功角的动态过程进而判断系统稳定性。根据式（7），得到VSG并网系统的Phillips-Heffron模型，如图3所示。

根据引入VPSS前的振荡模式实部ξVSG，适当选取引入VPSS后振荡模式实部ξVSG1，并代入式（16）以求取DVPSS，将DVPSS代入式（17），则可求取VPSS参数。

根据式（14）～式（17）可知，只要将系统的振荡模式传递给VPSS，即可完成对系统极点的调整及阻尼的提升。

3 算例分析

3.1 VSG低频振荡模态分析

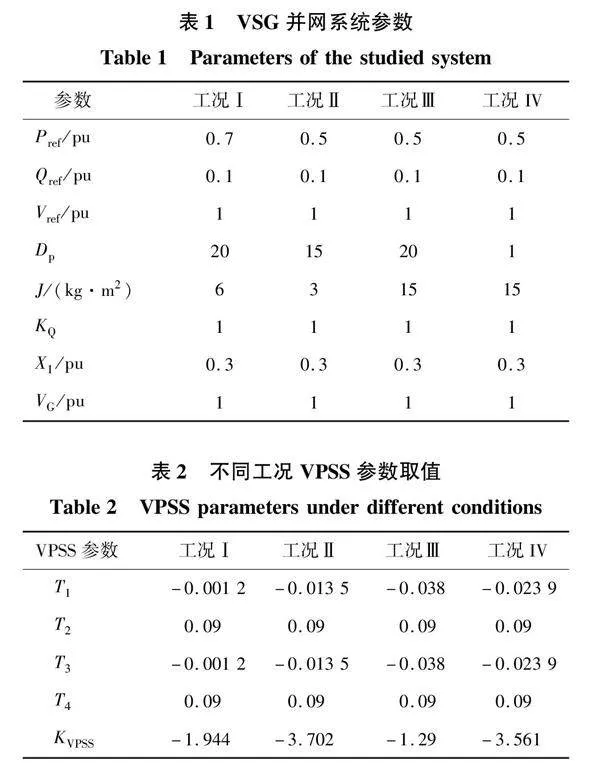
对于图1所示系统，设置四种工况如表1所示。其中，工况Ⅰ对应传统“低频”范畴（0.1～2.5 Hz）的振荡模式，但考虑到VSG参数灵活可调的特点，工况Ⅱ设定为频率略高的振荡模式（f≈3 Hz），以测试VPSS的适应性，工况Ⅲ为常规低频振荡模式，工况Ⅳ对应临界阻尼，测试VPSS在极端工作条件下维持系统稳定运行的能力。

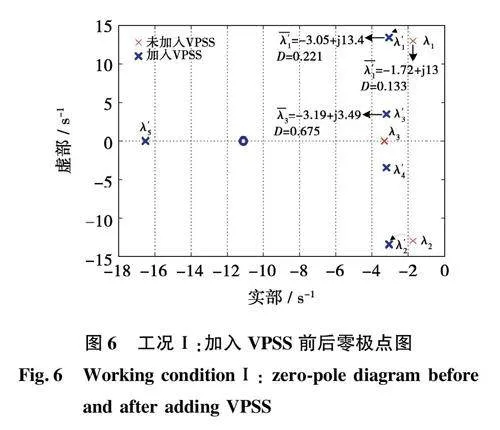
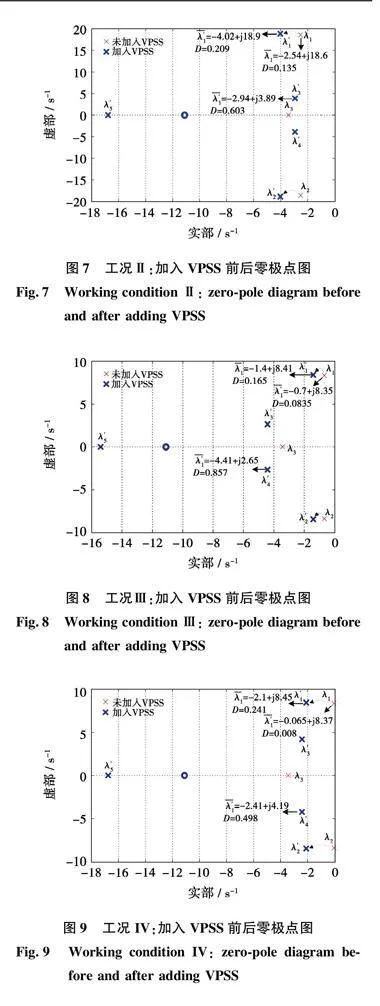
根据系统状态矩阵A，得到引入VPSS前，四种工况下的振荡模式。Ⅰ：λ1，2=－1.72±j13，Ⅱ：λ1，2=－2.54±j18.6，Ⅲ：λ-1，2=－0.7+j8.35，IV： λ1，2=－0.065±j8.37。假设计及VPSS接入的系统振荡模式分别为，Ⅰ：λ′1，2=－3±j13，Ⅱ：λ′1，2=－4±j18.6，Ⅲ：λ-1，2=－1.4+j8.35，IV：λ′1，2=－2.1±j8.37，其中，工况IV属于临界阻尼工况，此处将其极点大幅左移以试验在该极端工况下VPSS性能。将设定后的系统极点代入式（14）～式（17），可得VPSS参数，如表2所示。

根据所得参数，计算加入VPSS后的系统特征根，并将其与不含VPSS的情况进行对比，得到4种工况下的零极点分布分别如图6～图9所示。

根据图6～图9可知，VPSS的接入可按设定值准确影响系统极点，使4种工况的阻尼比分别得到提升；在工况IV临界阻尼的条件下，阻尼比提升更大，可显著改善VSG并网系统稳定性。与之相比，4种工况下系统振荡频率仅略微增加，说明VPSS对振荡频率的影响可忽略不计。

需要注意的是，VPSS对工况Ⅱ阻尼比提升不如工况Ⅰ，说明VPSS更适应于低频段。此外，VPSS的引入为系统增加了一对新的振荡模式，由于较高的阻尼比，其对系统稳定性影响不大；但随着系统的极点左移，VPSS自身极点将右移，故须根据实际工况确定接入VPSS后系统极点位置。

3.2 仿真验证

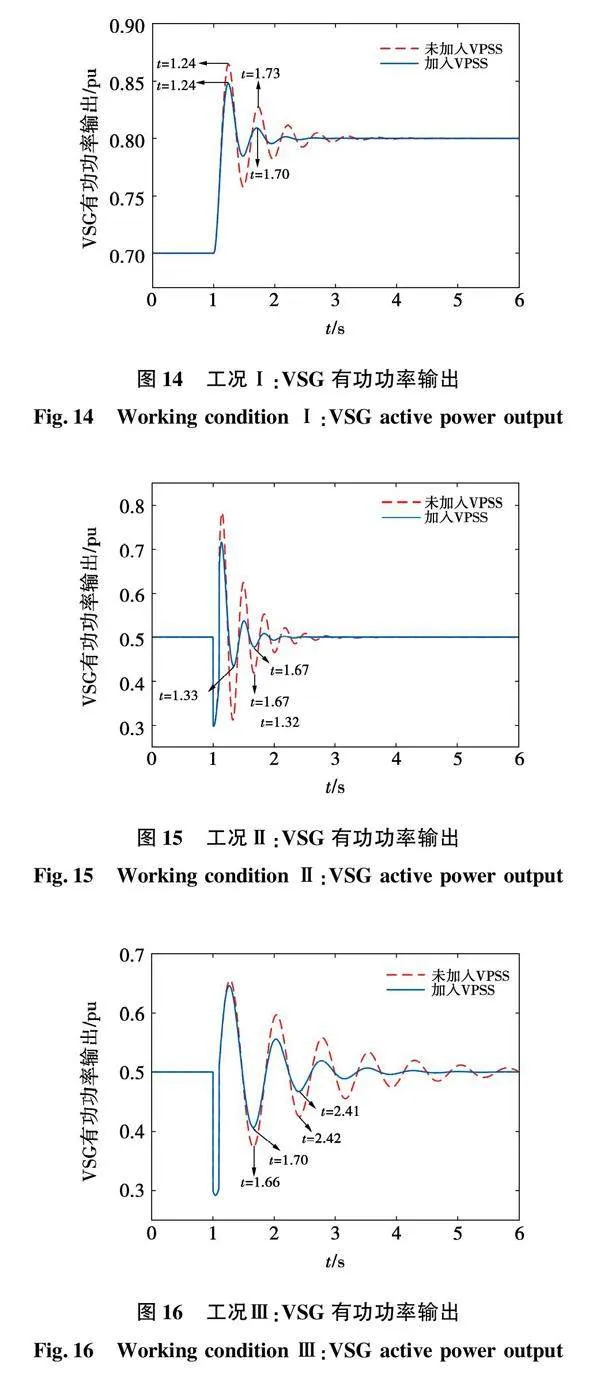
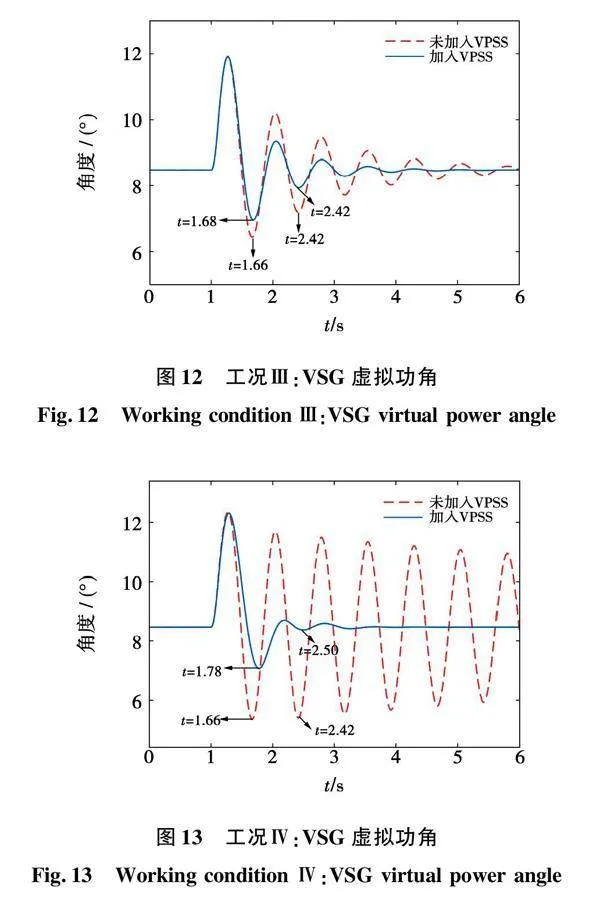
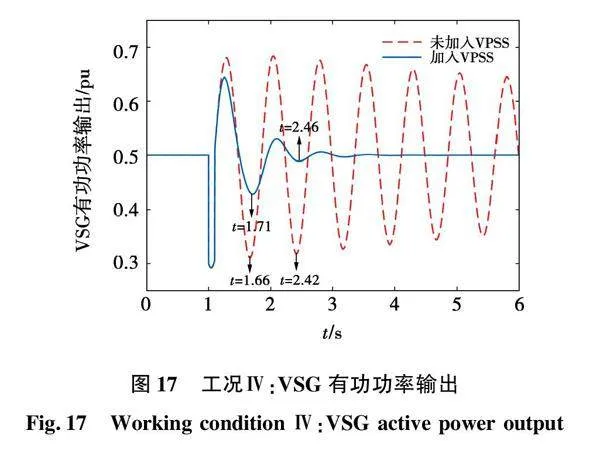
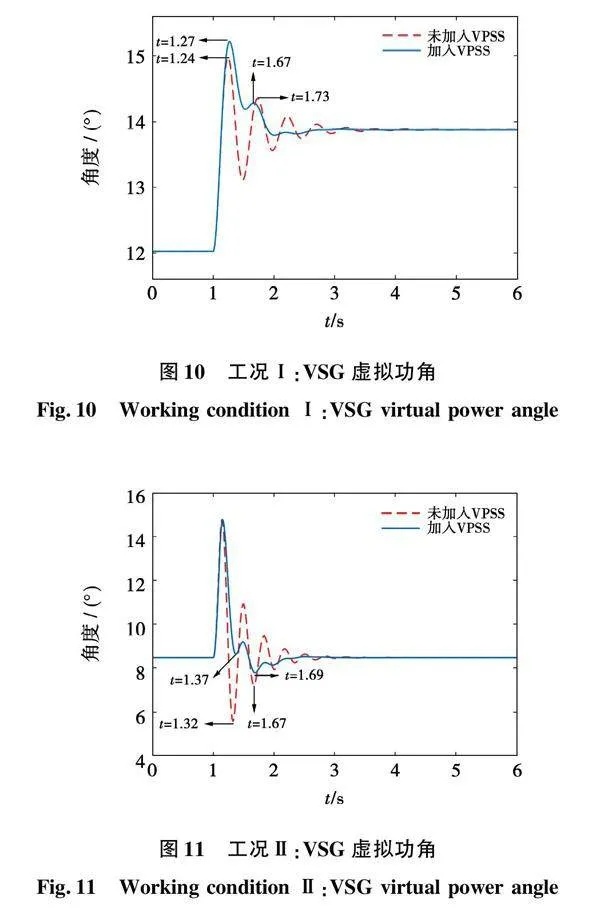
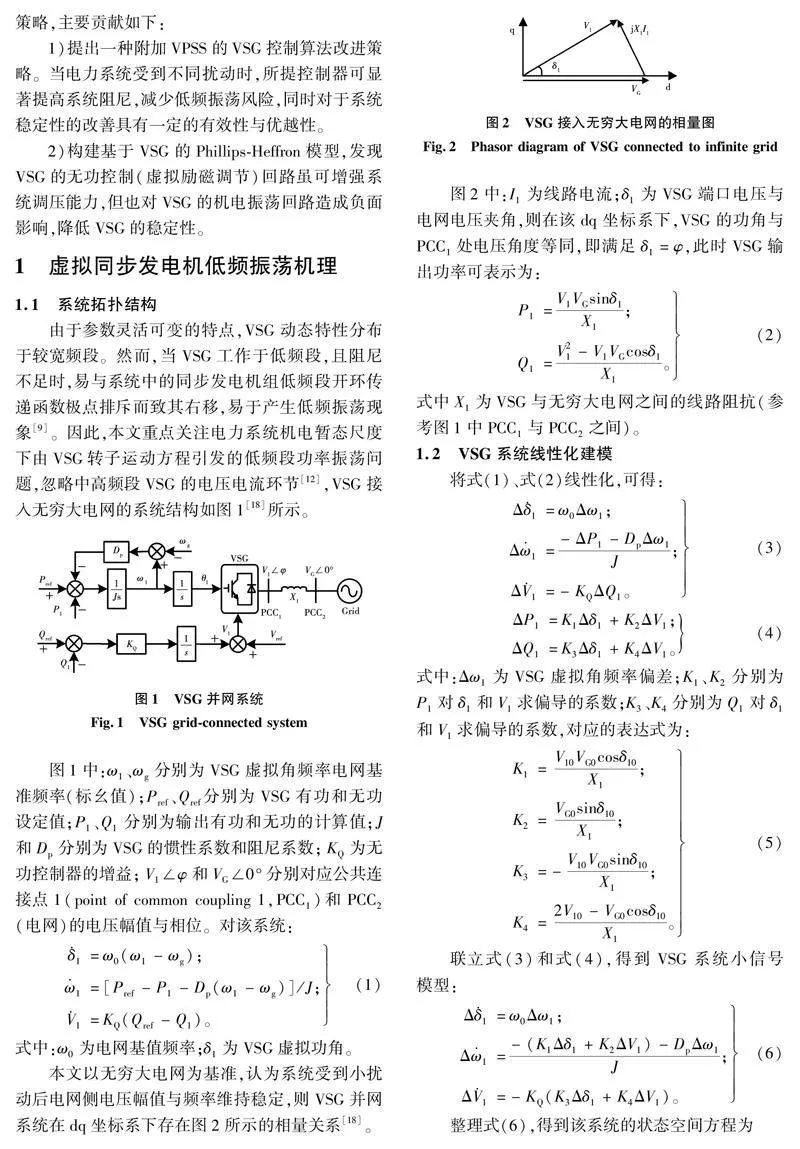
为验证本文提出的VPSS的有效性与正确性，在MATLAB/Simulink平台搭建了VSG并网系统的仿真模型，系统参数可参考表1，VPSS参数取表2计算所得的结果。在0～1 s，系统处于稳定运行状态，VSG虚拟功角和有功功率维持稳定。对于工况Ⅰ，在t=1 s时设置有功功率从0.7 pu阶跃至0.8 pu，对于工况Ⅱ、工况Ⅲ和工况IV，在t=1 s时令PCC2处发生短路故障，t=0.1 s时将故障切除。此时，4种工况下VSG虚拟功角的变化规律如图10～图13所示，VSG有功功率的振荡情况如图14～图17所示。

对于工况Ⅰ，根据图10、图14可知，接入VPSS后经历功率阶跃，虚拟功角在受到扰动后的一瞬间较不接入VPSS到达了更高峰，是由于VPSS参数不能完全匹配新运行点所致。但系统回到稳定运行状态的时间显著缩短，可见系统鲁棒性得到了提高。实际上，与SG类似，只要虚拟功角不超过系统稳定运行极限，则可维持系统稳定运行。

对于工况Ⅱ，根据图11、图15可知，含VPSS的VSG受到扰动后收敛迅速，且功率波动产生的第一个尖峰的幅值明显降低。

对于工况Ⅲ，根据图12、图16可知，当未引入VPSS，由于虚拟惯量较大，系统受到扰动虚拟功角和有功功率振幅明显且难以平息，需要约5 s才可恢复稳定运行。引入VPSS后，受到扰动后出现的振荡收敛明显加快，系统在不到3 s就基本回到稳定运行点，表明系统阻尼得到了显著提升，VPSS在该工况下对振荡抑制效果良好。

对于工况IV，根据图13、图17可知，由于极低的阻尼，系统遭受扰动后不含VPSS的VSG虚拟功角和输出有功振荡幅度较大，收敛较慢，阻尼特性较差，当其与传统电网相连时，极易发生功率失稳现象。与之相比，计及VPSS接入的VSG虚拟功角和输出有功受扰后迅速收敛，振荡幅值远小于传统VSG。此外，由于工况Ⅲ设定的VPSS将系统极点大幅左移，其阻尼在三种工况中最大，接入VPSS后，工况Ⅲ在受到扰动时振荡周期更短，更快回到正常运行状态。

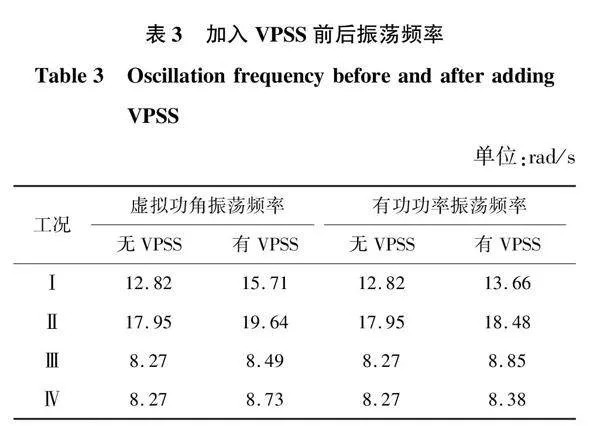
4个典型工况下仿真及理论研究证明了VPSS对于低频振荡抑制的有效性，能为系统提供正阻尼。此外，为验证理论正确性，根据读取的振荡周期，求得加入VPSS前后实测振荡频率如表3所示。

显然，在误差范围内，仿真结果与3.1章节的理论分析结果一致，加入VPSS后四种工况下系统振荡频率略微增加，在基本不影响振荡模式的前提下，一定程度上提升了系统的动态响应速度，更有利于频率稳定性。

4 结 论

本文参考同步机的Phillips-Heffron建模思路，通过将VSG系统线性化，构造了适用于VSG的Phillips-Heffron模型。其次，将影响VSG稳定性的参数等效为转矩ΔT，揭示了VSG低频振荡机理。

为此，借鉴PSS的设计方法，本文提出了一种适用于VSG低频振荡抑制的VPSS策略，并给出了其一般结构与优化方法。通过对比VPSS加入前后的系统极点位置，证明了VPSS可明显提高系统阻尼，仿真曲线的振荡特性验证了极点分析的正确性。此外，提出的VPSS具有可根据系统运行情况配置极点位置的优点，对于VSG并网稳定性的改善具有一定的促进作用。最后，时域仿真验证了将所提VPSS接入系统可在几乎不影响振荡频率的前提下，实现0.1～3 Hz下VSG低频振荡的有效抑制。

参 考 文 献：

［1］张智刚， 康重庆. 碳中和目标下构建新型电力系统的挑战与展望[J]. 中国电机工程学报， 2022， 42（8）： 2806.

ZHANG Zhigang， KANG Chongqing. Challenges and prospects for constructing the new-type power system towards a carbon neutrality future[J]. Proceedings of the CSEE， 2022， 42（8）： 2806.

［2］刘欣， 郭志博， 贾焦心， 等. 基于序阻抗的虚拟同步发电机并网稳定性分析及虚拟阻抗设计[J]. 电工技术学报， 2023， 38（15）： 4130.

LIU Xin， GUOZhibo， JIA Jiaoxin， et al. Stability analysis and virtual impedance design of virtual synchronous machine based on sequence impedance[J]. Transactions of China Electrotechnical Society， 2023， 38（15）： 4130.

［3］孙大卫， 刘辉， 李蕴红， 等. 风火/光火打捆系统中逆变电源调频与惯量控制对低频振荡的影响机理[J]. 中国电机工程学报， 2021， 41（17）： 5947.

SUN Dawei， LIU Hui， LI Yunhong， et al. Effect mechanism of primary frequency and virtual inertia control of inverter power on low-frequency oscillation in wind-thermal/solar-thermal bundled system [J]. Proceedings of the CSEE， 2021， 41（17）： 5947.

［4］TAMRAKAR U， SHRESTHA D， MAHARJAN M， et al. Virtual inertia： current trends and future directions[J]. Applied Sciences， 2017， 7（7）： 654.

［5］ZHONG Q C， WEISS G. Synchronverters： inverters that mimic synchronous generators[J]. IEEE Transactions on Industrial Electronics， 2011， 58（4）： 1259.

［6］孙大卫， 刘辉， 吴林林， 等. 虚拟同步发电机对低频振荡的影响建模与特性分析[J]. 电力系统自动化， 2020， 44（24）： 134.

SUN Dawei， LIU Hui， WU Linlin， et al. Modeling and characteristic analysis on influence of virtual synchronous generator on low-frequency oscillation[J]. Automation of Electric Power Systems， 2020， 44（24）： 134.

［7］于彦雪， 关万琳， 陈晓光， 等. 基于序阻抗的虚拟同步机同步频率谐振现象[J]. 电工技术学报， 2022， 37（10）： 2584.

YUYanxue， GUAN Wanlin， CHEN Xiaoguang， et al. Synchronous frequency resonance in virtual synchronous generator based on sequence-impedance[J]. Transactions of China Electrotechnical Society， 2022， 37（10）： 2584.

［8］谢小荣， 贺静波， 毛航银， 等. “双高”电力系统稳定性的新问题及分类探讨[J]. 中国电机工程学报， 2021， 41（2）： 461.

XIE Xiaorong， HE Jingbo， MAO Hangyin， et al. New issues and classification of power system stability with high shares of renewables and power electronics[J]. Proceedings of the CSEE， 2021， 41（2）： 461.

［9］DU W J， FU Q， WANG H F. Power system small-signal angular stability affected by virtual synchronous generators[J]. IEEE Transactions on Power Systems， 2019， 34（4）： 3209.

［10］马燕峰， 郑力文， 霍亚欣， 等. 虚拟同步发电机接入电力系统的阻尼转矩分析[J].电力自动化设备，2020，40（4）：166.

MA Yanfeng， ZHENG Liwen， HUO Yaxin， et al. Damping torque analysis of virtual synchronous generator connected to power system[J]. Electric Power Automation Equipment， 2020， 40（4）： 166.

［11］刘倪， 张昌华， 廖丽， 等. 计及无功电压环节的VSG虚拟转矩及振荡失稳机理分析[J]. 电力系统自动化， 2019， 43（6）： 107.

LIU Ni， ZHANG Changhua， LIAO Li， et al. Analysis on virtual torque and oscillation instability mechanism of virtual synchronous generator with reactive power-voltage controller[J]. Automation of Electric Power Systems， 2019， 43（6）： 107.

［12］王光宇， 付立军， 胡祺， 等. 计及电压环影响的虚拟同步发电机低频振荡阻尼分析与控制[J]. 电力系统自动化， 2022， 46（14）： 177.

WANG Guangyu， FU Lijun， HU Qi， et al. Analysis and control of low-frequency oscillation damping of virtual synchronous generator considering influence of voltage loop[J]. Automation of Electric Power Systems， 2022， 46（14）： 177.

［13］CHENG H， SHUAI Z， SHEN C， et al. Transient angle stability of paralleled synchronous and virtual synchronous generators in islanded microgrids[J]. IEEE Transactions on Power Electronics， 2020， 35（8）： 8751.

［14］孙久亮， 蔡蔚， 郭庆波. 基于虚拟阻抗优化的VSG暂态功角稳定自适应控制策略[J]. 电机与控制学报， 2024， 28（1）： 35．

SUN Jiuliang， CAI Wei， GUO Qingbo. Improvement of transient stability performance of VSG considering power angle stability and fault current limiting[J]. Electric Machines and Control， 2024， 28（1）： 35.

［15］WANG W， JIANG L， CAO Y， et al. A parameter alternating VSG controller of VSC-MTDC systems for low frequency oscillation damping[J]. IEEE Transactions on Power Systems， 2020， 35（6）： 4609.

［16］LI M X， YU P， HU W H， et al. Phase feedforward damping control method for virtual synchronous generators[J]. IEEE Transactions on Power Electronics， 2022， 37（8）： 9790.

［17］XIONG X， WU C， BLAABJERG F. An improved synchronization stability method of virtual synchronous generators based on frequency feedforward on reactive power control loop[J]. IEEE Transactions on Power Electronics， 2021， 36（8）： 9136.

［18］曾德银， 姚骏， 张田， 等. 虚拟同步发电机多机并联系统的频率小信号稳定性分析研究[J]. 中国电机工程学报， 2020， 40（7）： 2048.

ZENG Deyin， YAO Jun， ZHANG Tian， et al. Research on frequency small-signal stability analysis of multi-parallel virtual synchronous generator-based system [J]. Proceedings of the CSEE， 2020， 40（7）： 2048.

［19］ELLIOTT R T， ARABSHAHI P， KIRSCHEN D S. A generalized PSS architecture for balancing transient and small-signal response[J].IEEE Transactions on Power Systems，2019，35（2）：1446.

［20］ZHANG G， HU W， CAO D， et al. Deep reinforcement learning-based approach for proportional resonance power system stabilizer to prevent ultra-low-frequency oscillations[J]. IEEE Transactions on Smart Grid， 2020， 11（6）： 5260.

［21］高郭冰， 王蕾， 刘洋， 等. 利用电网拓扑优化提高含风电系统的静态电压稳定性[J]. 哈尔滨理工大学学报， 2022， 27（4）： 63.

GUO Xiaobing， WANG Lei， LIU Yang， et al.Static voltage stability improvement of wind power system by network topology optimization[J]. Journal of Harbin University of Science and Technology， 2022， 27（4）： 63.

［22］朱军， 袁亚飞， 刘鹏辉， 等. 基于功率微分项的双VSG有功功率振荡抑制策略[J].电机与控制学报，2024，28（1）：177．

ZHU Jun， YUAN Yafei， LIU Penghui， et al. Active power oscillation suppression strategy for dual-VSG grid based on power differential term[J].Electric Machines and Control，2024，28（1）：177.

（编辑：刘素菊）

收稿日期： 2022-12-23

基金项目：高等学校学科创新引智计划（D23005）；国网辽宁省电力有限公司\"揭榜挂帅\"科技攻关项目（2021YF-82）;辽宁省教育厅科技项目（LQGD2019005）

作者简介：王海鑫（1989—），男，博士，副教授，研究方向为综合能源系统优化运行、电力系统稳定性分析与控制等；

何海文（1998—），男，硕士研究生，研究方向为多能源系统与电力网络分析；

刘铭崎（1998—），男，硕士研究生，研究方向为多能源系统与电力网络分析；

杨子豪（1995—），男，博士研究生，研究方向为电力系统分析与控制；

郝 炎（1999—），男，硕士研究生，研究方向为多能源系统与电力网络分析；

杨俊友（1963—），男，博士，教授，研究方向为智能电网、新能源发电技术、新能源消纳技术等；

陈 哲（1955—），男，博士，教授，研究方向为风能和新能源现代电力系统等。

通信作者：杨俊友