永磁同步电机非线性增益非奇异快速终端滑模控制

摘 要：为了研究传统滑模控制中系统误差在有限时间内无法收敛至0以及传统滑模控制中系统抖振与收敛速度互不兼容的问题，提出一种非奇异快速终端滑模控制与扰动观测器结合的速度控制器。通过将参数可变的非线性函数作为增益代替固定增益加入滑模控制策略中从而改善系统响应速度同时减小系统的抖振。针对转矩扰动对系统的影响，加入负载转矩扰动观测器并补偿到q轴电流中以进一步提高控制器抗负载扰动能力。根据李雅普诺夫稳定性理论对提出的新型滑模控制器进行稳定性证明，经过仿真和实验证明，电机在启动时响应快、无超调且抖振较小，在突加转矩时转速波动小且恢复时间迅速，证明了改进后的变增益非奇异终端滑模控制与传统非奇异快速终端滑模控制策略相比可以提高动态性能的同时抑制系统抖振、增强系统的鲁棒性。

关键词：永磁同步电机；速度控制器；非奇异快速终端滑模；趋近率；扰动补偿

DOI：10.15938/j.emc.2024.05.000

中图分类号：TM351文献标志码：A

Nonlinear gain non-singular fast terminal sliding mode control for permanent magnet synchronous motors

KANG Erliang YU Haotian HAN Kangwei2

（1.Engineering Technology Research Center of High Efficiency Direct-Drive System in Universities in Heilongjiang，Harbin University of Science and Technology，Harbin 150080，China; 2.Technical Center for Mechanical and Electrical Product Inspection and Testing of Shanghai Customs District， Shanghai 200030， China）

Abstract：To address the challenges of system error non-convergence and buffeting-convergence incompatibility in traditional sliding mode control， a speed controller is proposed， combining non-singular fast terminal sliding mode control with a disturbance observer. This controller incorporates a nonlinear function with variable parameters as gain， enhancing system response and reducing buffeting. A load torque disturbance observer is added to improve anti-load disturbance ability. Lyapunov theory verifies the stability of this controller. Simulations and experiments confirm its fast response， no overshoot， and reduced buffeting. Compared to traditional methods， this improved variable gain control enhances dynamic performance， suppresses buffeting， and improves system robustness.

Keywords：permanent magnet synchronous motor; speed controller; non-singular fast terminal sliding mode; reaching law; disturbance compensation

0 引 言

电机作为电能的主要消耗元件在现代社会中占据重要的地位，而其中永磁同步电机（permanent magnet synchronous motor，PMSM）因其具有功率密度高、体积小等诸多优点，从而在工业和民用驱动控制中得到了广泛应用[1-4]，对PMSM的控制要求也在变高。比例积分控制作为应用最为广泛的传统线性控制方法，在PMSM调速场合成为其主流控制方法[5]。虽然PI控制具有算法简单、方便调试等优点，但是在实际控制中因为PMSM具有内部未建模的扰动和外部干扰等PI控制器无法消除的不确定因素，已经逐渐不能满足如今日益增长的对于PMSM控制的高性能要求[6-9]。

滑模控制（sliding mode control，SMC）作为非线性控制，可以使被控量在动态过程中根据系统当前的状态，有目的做小幅度、高频率的滑动来接近设定量，使系统对内部参数变化和外部扰动不灵敏来获得高鲁棒性[10-11]，从而满足电机控制对于系统高性能控制的要求，其在航空航天、新能源汽车、机器人等领域得到广泛应用[11-12]。

近年来众多学者为了进一步提升滑模控制性能，提出了诸多想法并得到了应用。文献[13]在新型可变非奇异滑模面的基础上引入转矩观测器来提升响应速度并增强其鲁棒性。文献[14]通过构建了一种非奇异快速积分滑模面来避免微分函数产生的噪声并提升收敛速度。文献[15]将模糊控制引入非奇异快速终端滑模来增强其鲁棒性。但是以上文献均未解决控制器中不连续项引起的抖振问题。文献[16]通过终端吸引子函数替代不连续函数来避免抖振现象的产生，但是计算复杂且参数难以确定。文献[17]将扰动滑模观测器与滑模速度控制器相结合以并削弱抖振，但是2种滑模算法的复合结构增加了算法复杂性。文献[18]通过终端吸引子函数替代不连续函数来避免抖振的产生，但是也存在计算复杂的缺点。文献[19]引入一种基于新型符号函数并应用到滑模控制器的趋近率中，提升了响应速度，但是该方法需要实时观测电机负载转矩。文献[20]将自适应控制算法、神经网络算法与滑模控制相结合，增强了其响应速度和鲁棒性，但是需要大量训练且复合控制算法导致的算法复杂问题。

本文将与误差有关的可变函数当作系数引入非奇异快速终端滑模面和控制器中，同时引入转矩观测器将对控制器中的扰动项进行补偿。同传统滑模面相比，本文所设计的变增益非奇异快速终端滑模控制器（nonlinear gain non-singular fast terminal sliding mode control，NGNFTSMC）可以使系统误差快速趋近于0，加快滑模收敛速度，削弱传统滑模控制中为了追求高响应速度而在控制器中对不连续项选取高增益导致的抖振问题，降低负载转矩对控制系统的干扰，增强系统鲁棒性。

1 PMSM数学模型

PMSM作为非线性强耦合系统，在仿真计算时出于简化计算考虑时假设电机运行条件如下：

1）磁路不饱和，气隙磁场呈正弦分布；

2）三相定子绕组对称且相差120°；

3）忽略涡流及磁滞损耗。

基于以上条件，将PMSM在三相坐标系下的电压方程转换为以d-q坐标系下的电压方程，方程表示如下：

3 仿真与实验结果与分析

3.1 仿真结果与分析

为了验证以上算法，在MATLAB/Simulink中分别以NGNFTSMC和普通指数趋近率下的非奇异快速终端滑模（non-singular fast terminal sliding mode control，NFTSMC）为基础搭建仿真模型，调速系统控制框图如图2所示。

其中电流环采用传统PI控制，滑模面参数和新型变增益指数趋近率参数选取方法是根据电机参数、设计的式（5）滑模面模型参数和式（7）趋近率模型参数的取值定义，设置初始值仿真计算得到。滑模面参数为：α=0.7，β=250，γ=0.2，q=5，p=7，m1=m2=3/2；新型变增益指数趋近率参数为：k1=1.35，k2=0.4，k3=0.2，k4=6×105，δ1=0.5，δ2=0.3；扰动观测器增益λ=－7。电机主要参数如表1所示。

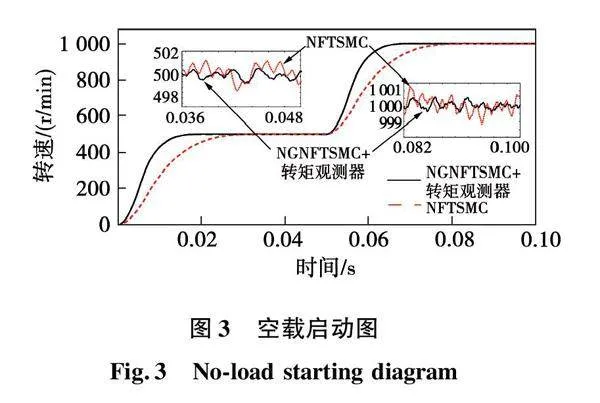
电机设置为空载启动参考转速设置为500 r/min，0.05 s时候参考转速突变为1 000 r/min。图3为2种控制策略下电机启动仿真结果。

由图3可以看出采用NGNFTSMC的方案在0.017 s左右上升到参考转速，而采用了NFTSMC的方案在0.03 s左右上升到参考转速，参考转速突变时采用了NFTSMC的方案相应相比传统NFTSMC拥有更快的响应速度。同时NGNFTSMC策略下在500 r/min时转速振动最大为0.7 r/min，小于NFTSMC控制策略下的1.5 r/min。在1 000 r/min时NGNFTSMC控制策略下转速抖振明显小于NFTSMC控制策略下的转速抖振。通过对比可以得出，采用NGNFTSMC策略的方法可以适应各种速域，响应更快，抖振更小且系统无超调。

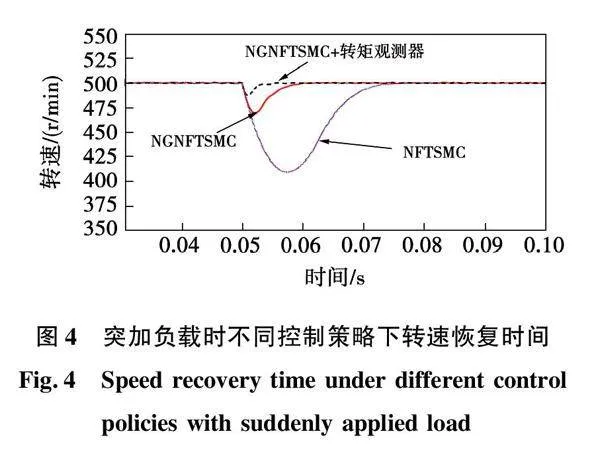
图4为参考转速500 r/min，在0.05 s突加5 N·m的负载转矩时不同控制策略下的转速响应，从图中可以得出单独应用NGNFTSMC策略下在突加负载时，电机转速下降28 r/min，经过0.01 s恢复至参考转速，而NFTSMC策略下在突加负载时，电机转速下降90 r/min，经过0.02 s仍未恢复至参考转速。将NGNFTSMC与转矩观测器相结合的控制策略下电机转速下降13 r/min，同时仅需0.006 s恢复至参考转速，由此可以得出NGNFTSMC策略的鲁棒性明显优于NFTSMC，加入转矩观测器前馈补偿的新型滑模控制策略可以进一步增强系统鲁棒性。

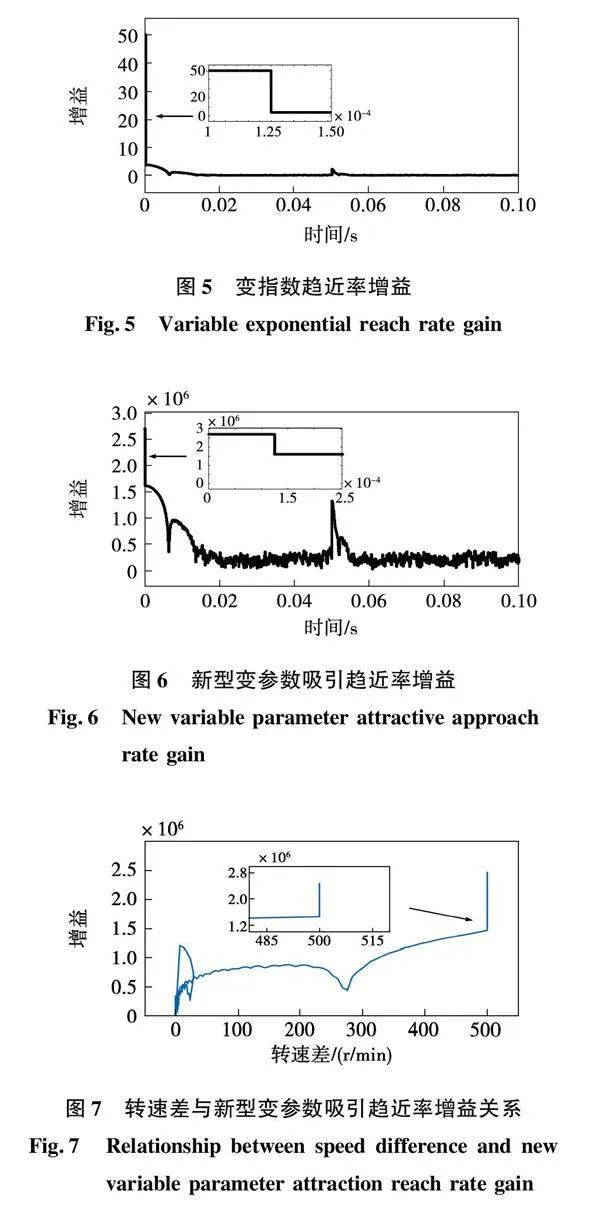
图5、图6为参考转速设置为500 r/min，在0.5 s突加10 N·m的负载转矩时的趋近率参数与时间变化曲线。图7为趋近率参数与转速差曲线。

由图5、图6中滑模变增益放大部分可知，电机在启动时刻滑模增益为最大值，电机转速随时间快速上升，随着电机转速上升增益逐渐减小并且最终稳定在一个较低区域来减小因为增益引起的抖振现象，在0.5 s突加10 N·m的负载转矩时电机因为转速突变而引起增益再次变大，使电机转速快速回到参考转速。1.25×10-4 s时的增益突变为此时转速上升，滑模面向零趋近，此时变增益趋近率因为指数衰减快速衰落，从而曲线近似表现为垂直减小。

由图7可以看出，电机空载启动时转速差最大，此时变参数吸引趋近率增益也为最大，增益整体随着转速差变小而逐渐变小。转速差为500 r/min时的增益大幅减小对应图6中1.25×10-4 s时的增益突变。转速差在0～50 r/min时再次出现的高增益对应图6中0.05 s时突加10 N·m的转矩导致的增益突变，可以看出此时增益变化远大于同转速差情况下空载时增益，印证了新型变增益趋近率鲁棒性更强。

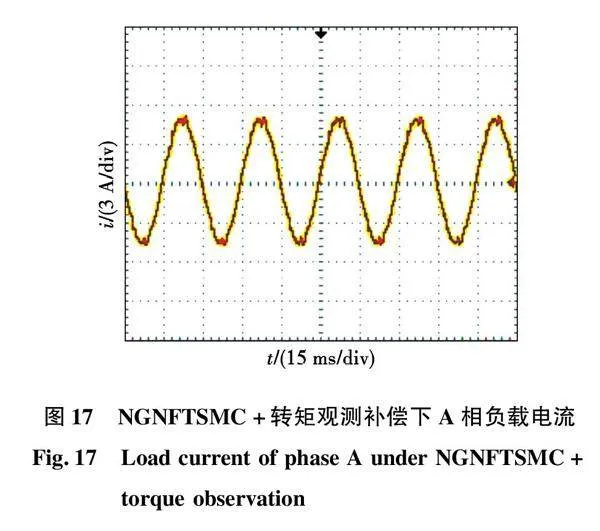
图8为参考转速500 r/min时不同δ2下的转速相应曲线，可以看出，当δ2取较大值（δ2=0.6）时，系统出现小超调导致响应速度变慢，抖振几乎不变，在滑动模态向稳定状态过渡时因为此时|s|小于1，此时增益整体偏小导致超调出现。当δ2取较小值（δ2=0.2）时抖振显著变大，这是因为k2|s|-δ2项减小，但是此时k3不能忽略不计，最终导致稳定时增益变大，使系统抖振变大，可以得出：选取适当的δ2可以在并不会使系统整体失去稳定性的前提下有效减小系统抖振。

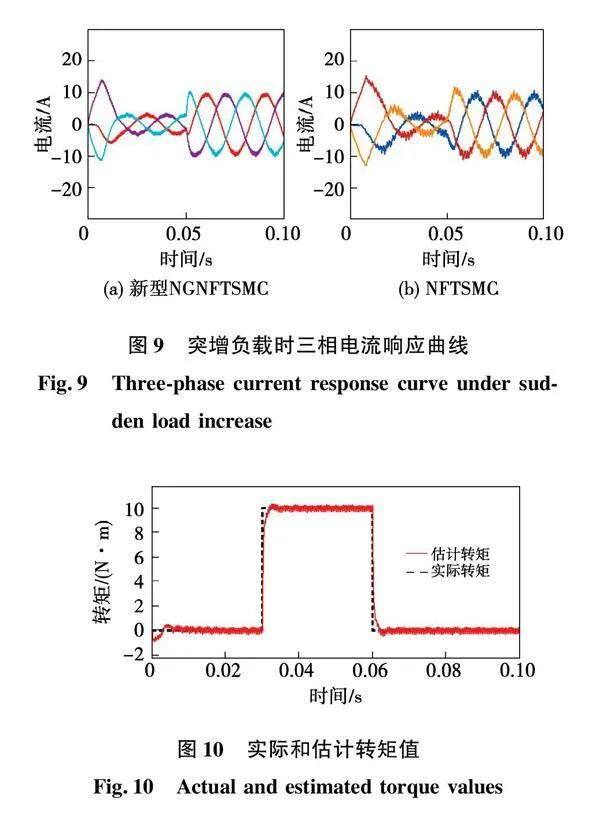
图9为初始负载3 N·m，参考转速500 r/min，0.05 s时负载变为10 N·m时的电流曲线，图9（a）为NGNFTSMC+转矩观测器控制策略下的电流响应曲线，图9（b）为NFTSMC控制策略下的电流响应曲线。通过对比可以得出：2种控制策略下定子三相电流都呈现三相正弦波形，但是NGNFTSMC+转矩观测器控制策略下的定子电流谐波更少，波形更趋近于标准三相正弦波，同时在启动和0.05 s加负载转矩时冲击电流更小，响应更快。

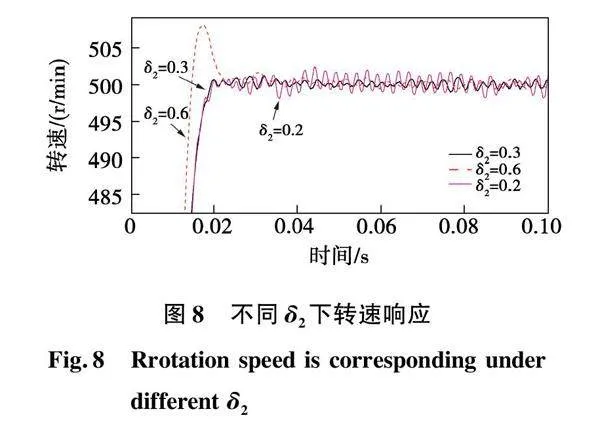
图10为给定转速500 r/min，在0.3 s对电机进行突加10 N·m和在0.6 s突然卸去所加转矩时的转矩观测量可以得出：该观测器可在0.2 s左右跟随至实际值，所观测转矩波动为0.5 N·m。图3～图9的仿真结果表明，NGNFTSMC+转矩观测补偿控制策略下的PMSM响应更快，抖振更小且鲁棒性更强，验证了所提出的新型滑模控制器理论正确性。

3.2 新型滑模控制系统实验验证

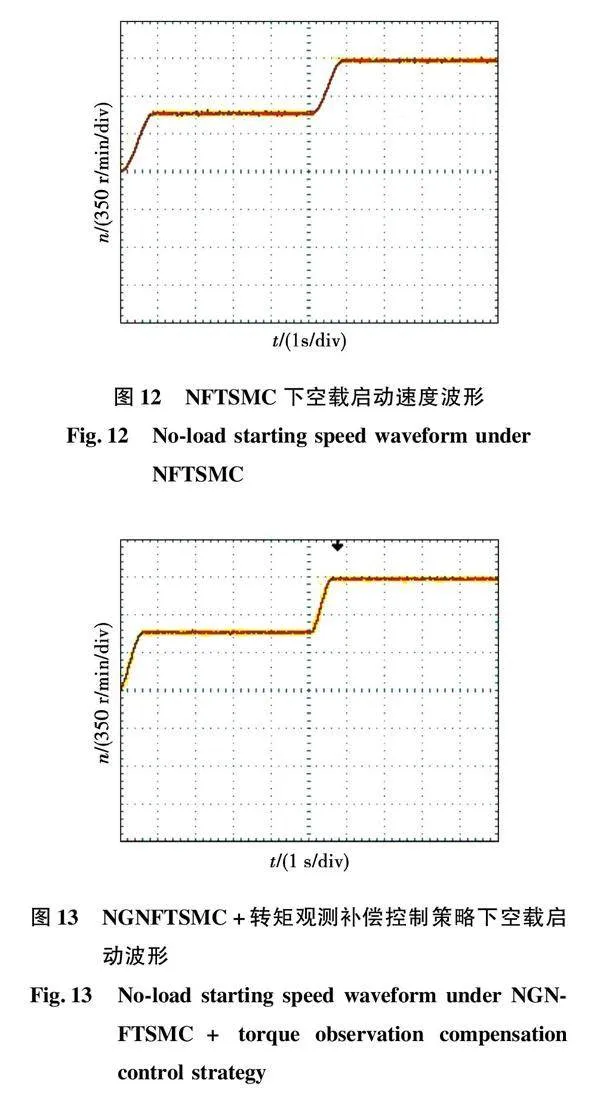
根据图2搭建的实验平台如图11所示，平台控制器基于DSP28335搭建而成，在实验中给定转速为500 r/min，5 s时给定转速突变为1 000 r/min，再以给定转速500 r/min为基础突加5 N·m负载转矩，通过示波器观察所得实验结果如图12～图18所示。

由图12、图13空载启动波形对比可得新型控制策略在0.5 s左右上升至给定转速，相较传统NFTSMC下的电机上升至指定转速时间（0.8 s）更快速，同时新型控制策略下系统无超调。在5 s时给定转速突变控制器仍可快速控制电机跟随至改变后的给定转速，2次转速上升时间均为0.5 s左右，实验结果与仿真结果大致相同。

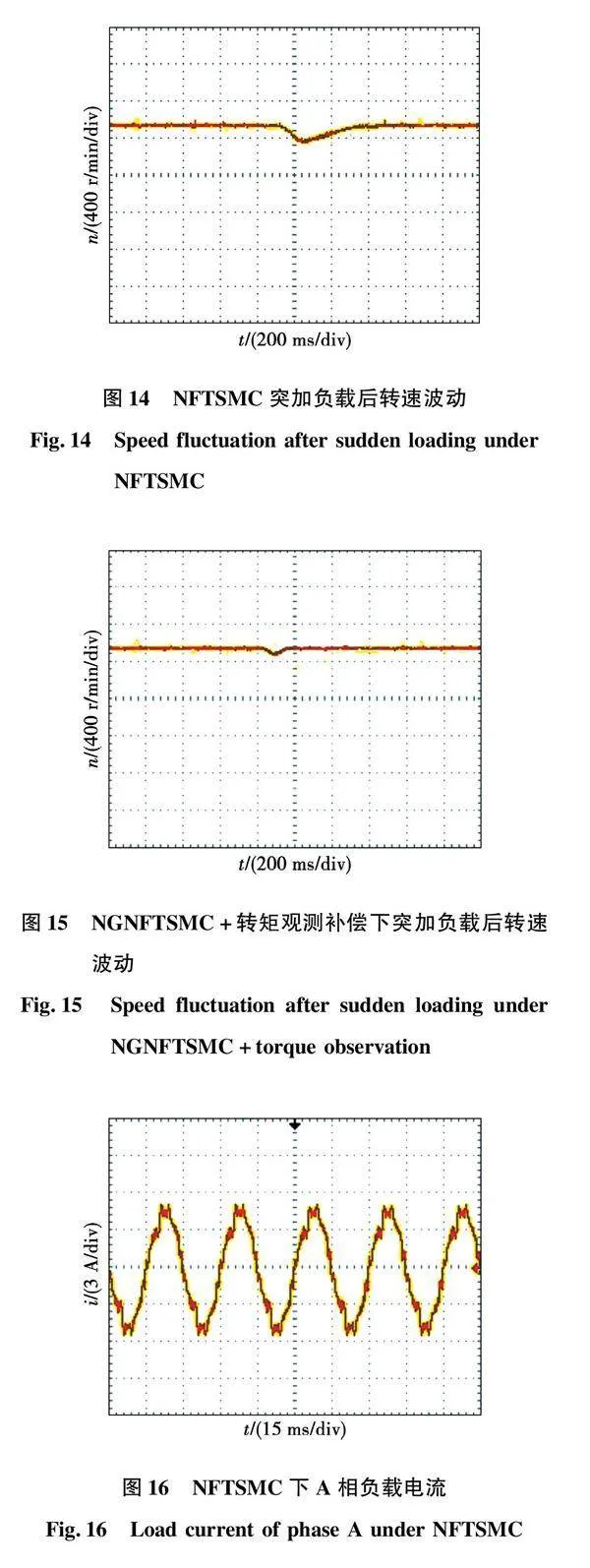
由图14、图15突加负载下转速波动图可知，NGNFTSMC+转矩观测补偿控制策略下电机在突加负载时转速下降为90 r/min，经过6 ms恢复至指定转速。而传统NFTSMC突加负载后转速波动为170 r/min，恢复时间为20 ms，对比可得NGNFTSMC+转矩观测补偿控制策略下系统响应速度更快，鲁棒性更强。

图16、图17分别为传统NFTSMC以及新型控制策略下的A相负载电流。此时电机给定转速为500 r/min，负载转矩5 N·m。由图可知NGNFTSMC+转矩观测补偿控制策略下负载电流相较NFTSMC下负载电流谐波更少，更类似于标准正弦，而传统NFTSMC下电流谐波较多。

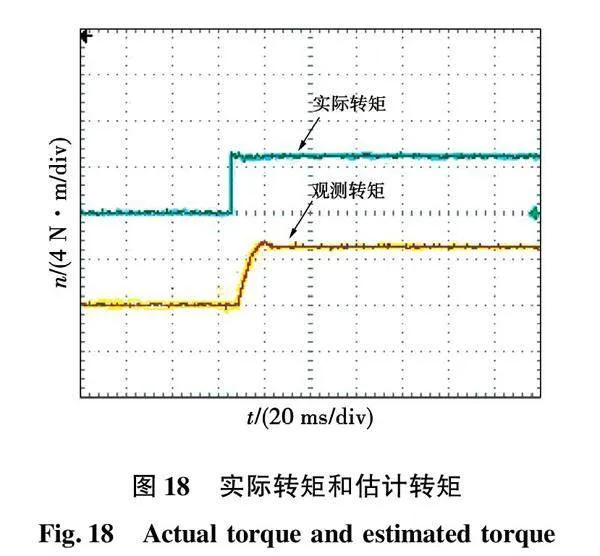
当突加负载时新型转矩观测器观测结果如图18所示，由图可知转矩观测器可在20 ms以内对负载转矩进行观测且最大观测误差为0.8 N·m，具有较高的观测精度，验证了新型转矩观测器的有效性。

4 结 论

本文采用了将可变增益引入非奇异快速终端滑模并与转矩观测器相结合的新型控制策略。通过在仿真中将可变增益对系统性能的影响进行分析并将其与传统NFTSMC进行不同情况下的性能对比，最后搭建PMSM实验平台，通过实验对仿真进行验证。结果表明，将变增益引入非奇异终端滑模控制后控制器中滑模增益值将随系统与滑模面距离变化而变化，从而加快了系统响应速度，削弱了抖振，增强了系统动态性能，而将NGNFTSMC与新型转矩观测器相结合的新型控制策略可以在NGNFTSMC的基础上进一步提高系统的抗负载扰动能力，经验证可以得出与传统NFTSMC相比其响应速度提升37.5%、抖振削弱53%，综合控制性能更好，而且遭受扰动时转速波动减小47%，扰动后的恢复时间仅需传统NFTSMC的0.3倍，拥有更强的鲁棒性。

参 考 文 献：

［1］WANG M S， SYAMSIANA I N， LIN F C. Sensorless speed control of permanent magnet synchronousmotors by neural network algorithm [J]. Mathematical Problems in Engineering， 2014， 50（4）： 1.

［2］HAN J， KIM B H， SUL S K. Effect of current measurement error in angle estimation of permanent magnet AC motor sensorless control[C]// IEEE 3rd International Future Energy Electronics Conference and ECCE Asia， July 27， 2017， Taiwan， China. 2017： 2171-2176.

［3］ALI N， REHMAN A， ALAM W， et al. Disturbance observer based robust sliding mode control of permanent magnet synchronous motor[J]. Journal of Electrical Engineering amp; Technology， 2019， 14（6）： 2531.

［4］吕德刚， 姜国威， 纪堂龙. 永磁同步电机低速域改进高频脉振注入控制[J].哈尔滨理工大学学报，2022，27（6）：32.

L Degang， JIANG Guowei， JI Tanglong. Improved high frequency pulse pnjection control in low speed domain of permanent magnet synchronous motor[J]. Journal of Harbin University of Science and Technology， 2022， 27（6）： 32.

［5］李垣江， 董鑫， 魏海峰， 等. 表贴式永磁同步电机转速环复合PI无位置传感器控制[J].电工技术学报，2020，35（10）：2119.

LI Yuanjiang， DONG Xin， WEI Haifeng， et al. Sensorless compound PI control for surface permanent magnet synchronous motor speed regulation system[J]. Transactions of China Electrotechnical Society， 2020， 35（10）： 2119.

［6］田艳丰， 郭庆鼎. 永磁直线同步电动机的滑模-H∞鲁棒跟踪控制[J].电工技术学报，2004，19（4）：2.

TIAN Yanfeng，GUO Qingding.Sliding mode-H∞ robustness tracking control for permanent magnet linear synchronous motors[J].Transactions of China Electrotechnical Society，2004，19（4）：2.

［7］宋璐， 卫亚博. 基于模糊PID的无刷直流电机速度控制系统的设计与仿真[J].大电机技术，2022（5）： 40.

SONG Lu， WEI Yabo. Design and simulation of speed control system of brushless DC motor based on fuzzy PID[J]. Large Electric Machine and Hydraulic Turbine， 2022（5）： 40.

［8］禹聪， 康尔良. 永磁同步电机模糊滑模速度控制器设计[J].电机与控制学报，2022，26（7）： 98.

YU Cong， KANG Erliang. Design of fuzzy sliding mode speed controller for permanent magnet synchronous motor[J]. Electric Machines and Control， 2022， 26（7）： 98.

［9］刘陆， 丁世宏， 李世华. 高阶滑模控制理论综述[J]. 控制理论与应用， 2022， 39（12）： 2193.

LIU Lu， DING Shihong， LI Shihua. A survey for high order sliding mode control theory[J]. Control Theory and Applications， 2022， 39（12）： 2193.

［10］刘金琨， 孙富春. 滑模变结构控制理论及其算法研究与进展[J].控制理论与应用，2007（3）： 407.

LIU Jinkun， SUN Fuchun. Research and development on theory and algorithms of sliding mode control[J]. Control Theory and Applications， 2007（3）： 407.

［11］陆婋泉， 林鹤云， 韩俊林. 永磁同步电机的扰动观测器无位置传感器控制[J].中国电机工程学报，2016，36（5）：1387.

LU Xiaoquan， LIN Heyun， HAN Junlin. Position sensorless control of permanent magnet synchronous machine using a disturbance observer[J].Prceedings of the CSEE，2016，36（5）：1387.

［12］FAN Y， ZHANG L， CHENG M， et al. Sensorless SVPWM-FADTC of a new flux-modulated permanent magnet wheel motor based on a wide-speed sliding mode observer[J]. IEEE Transactions on Industrial Electomnices， 2015， 62（5）： 3143.

［13］康尔良， 贺建智， 王一琛. 永磁同步电机非奇异终端滑模控制器的设计[J].电机与控制学报，2021，25（12）： 58.

KANG Erliang， HE Jianzhi， WANG Yichen. Design of non-singular fast terminal sliding mode controller for permanent magnet synchronous motors[J]. Electric Machines and Control， 2021， 25（12）： 58.

［14］郑诗程， 刘志鹏， 赵卫， 等.积分型非奇异终端滑模PMSM无传感器控制系统[J].电机与控制学报， 2024，28（3）： 169.

CHENG Shicheng， LIU Zhipeng， ZHAO Wei， et al. Integral non-singular terminal sliding mode PMSM sensorless control system[J]. Electric Machines and Control， 2024，28（3）：169.

［15］吴爱国， 吴绍华， 董娜. 机械臂非奇异快速终端滑模模糊控制[J].浙江大学学报（工学版），2019，53（5）： 862.

WU Aiguo， WU Shaohua， DONG Na， et al. Nonsingular fast terminal sliding model fuzzy control of robotic manipulators[J]. Journal of Zhejiang University （Engineering Science）， 2019， 53（5）： 862.

［16］黄依婷， 沈建新， 王云冲， 等. 基于递推最小二乘法观测器的永磁同步伺服电机变参数滑模控制[J].中国电机工程学报，2022，42（18）： 6835.

HUANG Yiting， SHEN Jianxin， WANG Yunchong， et al. Variable parameter sliding mode control of permanent magnet synchronous servo machine based on recursive least square observer[J]. Proceedings of the CSEE， 2022， 42（18）： 6835.

［17］SUN X D， WU J L， LEI G， et al. Torque ripple reduction of SRM drive using improved direct torque control with sliding mode controller and observer[J]. IEEE Transactions on Industrial Electronics， 2021， 68（10）： 9334.

［18］蒲明， 吴庆宪， 姜长生， 等. 高阶滑模微分器的分析与改进[J].控制与决策，2011，26（8）： 1136.

PU Ming， WU Qingxian， JIANG Changsheng， et al. Analysis and improvement of higher-order sliding mode differentiator[J]. Control and Decision， 2011， 26（8）： 1136.

［19］SUN X D， XIONG Y F， YANG J F， et al. Torque ripple reduction for a 12/8 switched reluctance motor based on a novel sliding mode control strategy[J]. IEEE Transactions on Transportation Electrification， 2023， 9（1）： 359.

［20］魏惠芳， 王丽梅. 永磁直线同步电机自适应模糊神经网络时变滑模控制[J].电工技术学报，2022，37（4）： 861.

WEI Huifang， WANG Limei. Adaptive fuzzy neural net work time-varying sliding mode control for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society， 2022， 37（4）： 861.

（编辑：刘琳琳）

收稿日期： 2023-07-21

基金项目：国家重点研发计划项目（2020YFF0402198）

作者简介：康尔良（1967—），男，博士，教授，硕士生导师，研究方向为电机设计及其控制等;

于浩天（1997—），男，硕士研究生，研究方向为永磁同步电机控制等;

韩康玮（1982—），硕士，工程师，研究方向为新能源电力总成及机械电子。

通信作者：于浩天