电磁轨道发射器能量转换过程

摘 要：为提高电磁轨道炮发射效率，探讨电磁轨道发射器的能量转换过程及规律，依据电路和电动力学理论，构建了由动生阻抗、轨道电感、轨道电阻和枢轨接触电阻等组成的发射器非线性数学模型，搭建了耦合结构力、速度、位移等因素的发射器仿真模型，在分析动生阻抗、轨道电感、轨道电阻和枢轨接触电阻特性的基础上，揭示了发射器的脉冲电源激励、脉冲电源和轨道电感共同激励、轨道电感主激励三阶段能量转换规律，得到某次试验发射器能量转换过程和各负载消耗能量占比，其中轨道电阻消耗能量占比52.73%最高，降低轨道电阻、轨道电阻梯度和摩擦系数等仿真参数后，发射器效率由27.27%提升至60.87%。

关键词：电磁轨道炮；发射效率；能量转换；动生阻抗；轨道电阻；轨道电感

DOI：10.15938/j.emc.2024.05.000

中图分类号：TM89文献标志码：A

Analysis of energy conversion process in electromagnetic rail launcher

CHEN Shaohui1，2， WANG Jiong1，3， CHENG Wenping1，3， YAN Ping1，3，4， XU Weidong1，3

（1.Institute of Electrical Engineering， Chinese Academy of Sciences， Beijing 100190， China; 2.Beijing Aeronautical Technology Research Center， Beijing 100076， China; 3.Key Laboratory of Power Electronics and Power Drives， Chinese Academy of Sciences， Beijing 100190， China; 4.University of Chinese Academy of Sciences， Beijing 100049， China）

Abstract：To enhance the launch efficiency of the electromagnetic rail launcher， we discussed the energy conversion processes and rules， and constructed a nonlinear arithmetic model for the rail launcher based on electronic load and electrodynamics. Comprising motional impedance， rail inductance， rail resistance and armature-rail contact resistance， the model contributes to the establishment of a simulation model coupled with structural force， speed and displacement. We also analyzed the characteristics of motional impedance， rail inductance and rail resistance， and thereupon revealed the energy transport process as composed of three phases， respectively being pulse power supply excitation， followed by joint excitation of pulse power supply and rail inductance， and finally main excitation of rail inductance. Through several field experiments， we obtained the specific process of energy conversion and the energy consumption ratios of various loads， with the energy consumption by rail resistance being the highest （52.73%）." By reducing simulation parameters such as track resistance， track resistance gradient and friction coefficient， the transmitter efficiency is improved from 27.27% to 60.87%.

Keywords：electromagnetic railgun; launch efficiency; energy conversion process; motional impedance; rail inductance; rail resistance

0 引 言

电磁轨道发射技术是利用脉冲大电流流过轨道和电枢时产生极高安培力作为推力，在毫秒级时间内将电枢和有效载荷加速至每秒几千米的全新发射方式，具有初速高、发射成本低、速度易控制等优点，在军事、航天、科学研究等领域显示出巨大应用潜力[1]，但由于发射效率低、体积大、重量重等因素，制约了该技术在相关领域的推广应用［2-5］。

电磁轨道发射器作为电能转换为动能的直接载体，其能量转换效率直接决定系统发射性能，但发射器能量转换过程复杂，与电流、初始电阻、初始电感、电阻梯度、电感梯度等诸多因素相关，掌握其能量转换规律对研究提高系统发射效率具有重要意义［6-10］。

国内外专家和学者对电磁轨道发射效率开展了大量研究，主要集中在以下两个方面：一是在恒流或无能量损耗等假设条件下，基于简化理论模型，进行定性的理论推导分析，得到大致系统参数对发射效率的影响关系［11-15］，但无法推广至复杂实际系统；二是通过仿真或试验手段，开展系统参数优化和效率研究，简要分析数据变化趋势，得到有限范围内系统参数对发射效率的影响关系［16-22］，其有限的数据点不足以对发射效率的变化趋势进行全面细致的分析［23-24］。因此，本文将在理论分析和建模仿真的基础上进行试验验证，揭示发射器能量转换规律，对电磁轨道发射效率提高和发射器设计优化具有指导意义。

1 发射器数学模型

根据电路理论，电磁轨道发射器是一个非线性电气负载，整个电磁轨道发射器电压（即发射器尾部电压）构成如图1所示，算式表示为

由于有效载荷与轨道之间只有结构过盈引起的机械压力，因此有效载荷受到的摩擦力2f2可近似假设为固定值。

1.6 能量转换过程初步分析

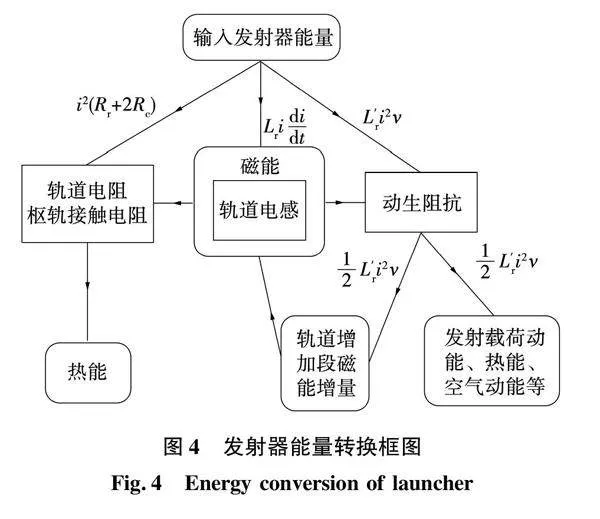
由式（5）和式（8）可知，发射器磁能变化主要与以下两方面有关：一是电枢运动引起载流轨道长度及相应磁能增加，二是电流变化导致载流轨道磁能变化。对于恒流无能量损耗理想情况，di/dt等于零，传输给发射器电感的电功率L′ridi/dt也为零，即在恒流情况下无能量输入或输出轨道电感。而传输给动生阻抗的能量一半转换为轨道磁能，另外一半通过电磁推力做功转换为发射载荷动能、摩擦热能、空气动能等。因此，在忽略电阻、摩擦、空气阻力等因素的恒流理想情况下，输入发射器的能量一半转换成轨道磁能，一半转换为发射载荷动能，其发射效率最高为50%[1]。

实际上电磁轨道发射系统很难实现无损耗恒流理想情况或实现代价太大无法满足工程需要，而是多采用梯形电流波形，下面结合图4所示的发射器能量转换图，理论分析电磁轨道实际发射过程中能量转换过程。该情况下动生阻抗的能量转换过程与无损耗恒流相同，输入动生阻抗的能量一半转换为轨道长度增量的磁能，另一半通过电磁推力做功转化为发射载荷动能、热能、空气动能等。轨道电感能量转换过程与无损耗恒流不同，由式（8）可知，当电流增大时（上升沿）di/dt为正值，轨道电感作为负载吸收磁能；当电流减小时（下降沿）di/dt为负值，轨道电感作为电源释放磁能，其中一部分能量传输给动生阻抗，一部分传输给轨道电阻和枢轨接触电阻，当电枢离开发射器时电流下降至较小值，存储在轨道电感中的大部分磁能得到释放。最终，脉冲功率电源传输给发射器的能量转变为三部分：轨道电阻和枢轨接触电阻的热能，发射载荷动能、摩擦热能、空气动能，剩余在轨道电感中磁能。例如，某次试验中上述三者的能量占比分别为53%、35%和12%。

由此可见，轨道电阻和枢轨接触电阻消耗了一半以上的能量，若想提高发射器发射效率，可降低轨道电阻和枢轨接触电阻。

2 电磁轨道发射器仿真模型及验证

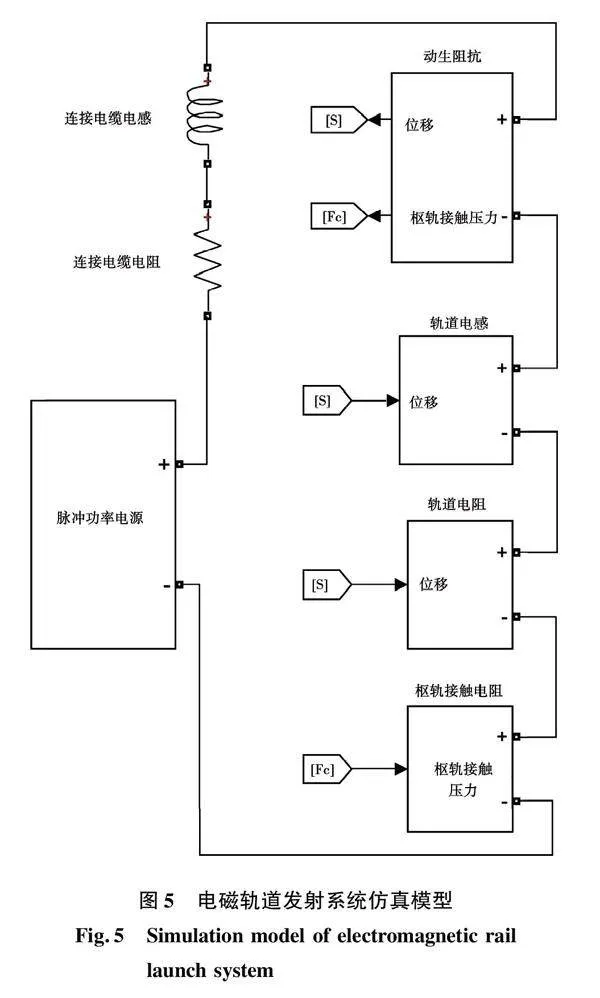
2.1 电磁轨道发射系统仿真模型

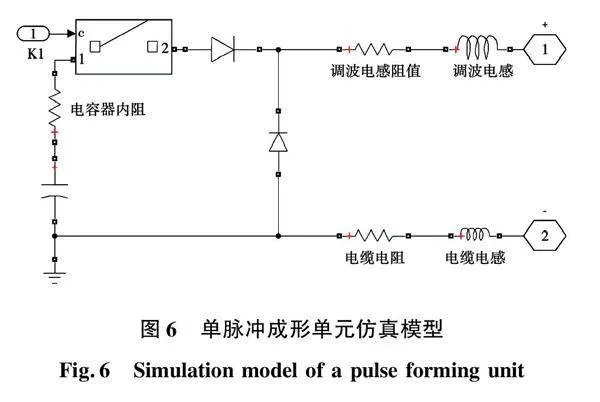
电磁轨道发射系统仿真模型如图5所示，主要由脉冲功率电源、动生阻抗、发射器电感、发射器电阻、枢轨接触电阻、连接电缆电阻和连接电缆电感组成。其中，脉冲功率电源由22个脉冲成形单元并联组成，通过控制脉冲成形单元的时序，获得梯形电流波形，单个脉冲成形单元仿真模型如图6所示，主要由电容器、电容器内阻、开关、二极管、续流二极管、调波电感、调波电感电阻、电缆电感、电缆电阻等组成。

2.2 动生阻抗仿真模型

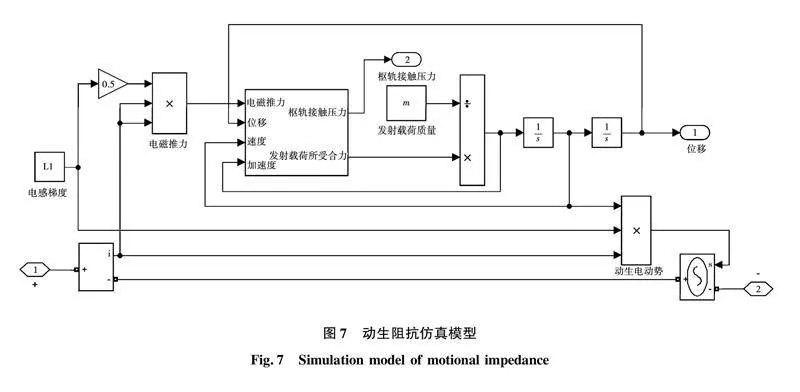
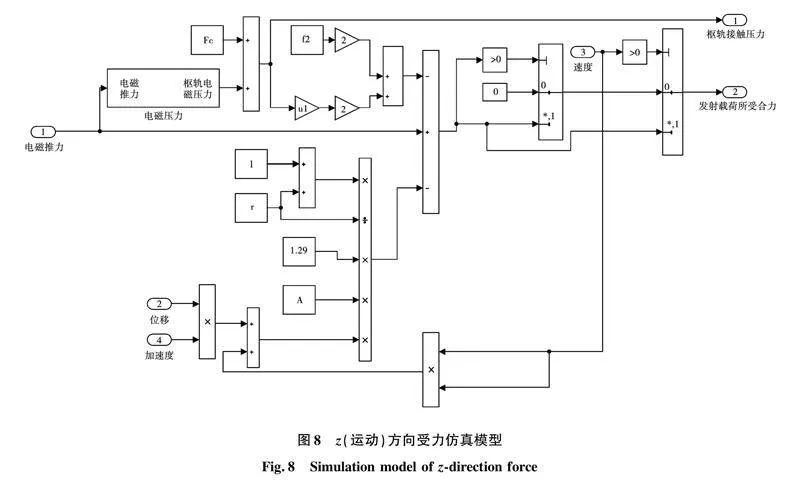
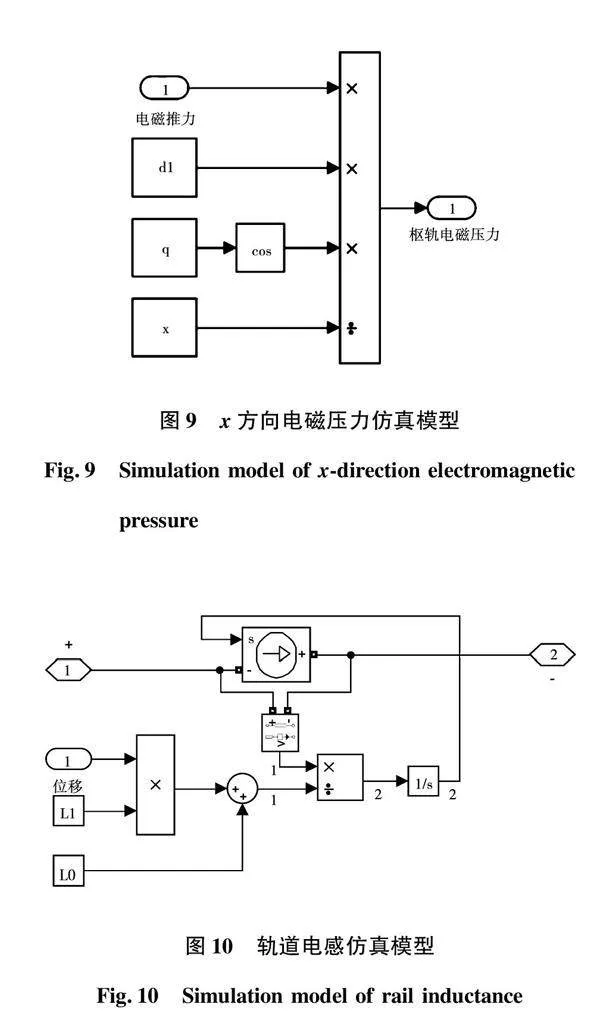
根据动生电动势式（2）、速度式（11）和发射载荷受力式（15），建立了如图7所示的动生阻抗仿真模型。该模型首先从系统电路中采集电流信号用于电磁推力计算；然后将结果输入图8所示z方向受力仿真模型，并结合如图9所示x方向电磁压力仿真模型，计算得到发射载荷在运动方向上电磁推力、摩擦力和空气阻力的合力；最后合力除以发射载荷质量得到加速度，进行积分得到发射载荷速度，再积分得到发射载荷位移，将速度、电感梯度和电流相乘得到动生电动势，并以受控电压源方式反馈至系统电路。

2.3 发射器电感仿真模型

对发射器电感电压式（8）两边进行积分得到电流表达式：

根据式（16）建立如图10所示的发射器电感仿真模型，从系统电路中采集发射器电感电压信号，除以发射器电感后进行积分，并将其结果通过受控电流源方式反馈至系统电路。其中，输入量位移来自动生阻抗仿真模型，发射器初始电感、电感梯度假设为定值，由仿真初始程序进行加载。

2.4 发射器电阻仿真模型

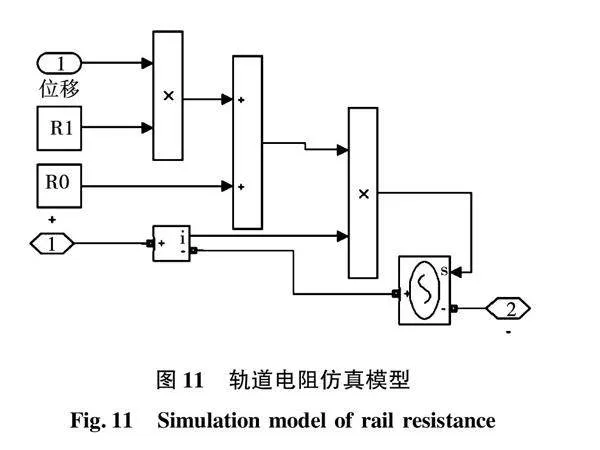
根据式（9）建立如图11所示的发射器电阻仿真模型，轨道初始电阻加上轨道电阻梯度与位移乘积后，与电流相乘得到轨道电阻电压，并通过受控电压源方式反馈回系统电路。其中，输入量位移来自动生阻抗仿真模型，轨道初始电阻和轨道电阻梯度假设为定值，由仿真初始程序进行加载。

2.5 枢轨接触电阻仿真模型

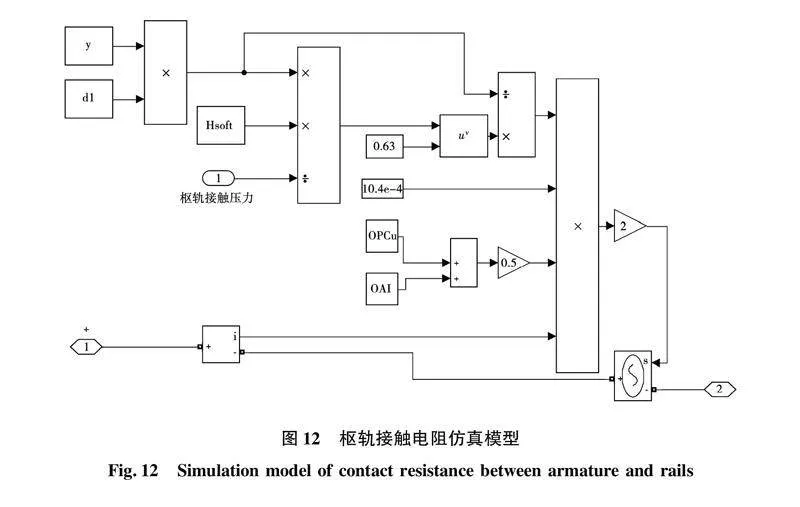
根据式（10）建立如图12所示的枢轨接触电阻仿真模型，将计算得到的数值通过受控电压源反馈至系统电路。

2.6 仿真验证

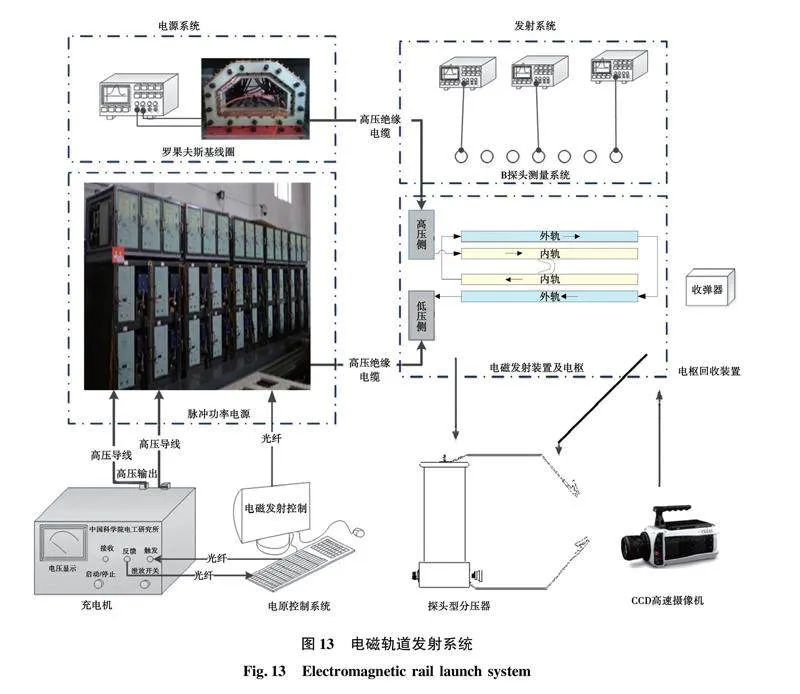
为验证上述发射器仿真模型的正确性，需要将仿真数据与试验数据进行对比分析，本文所采用的电磁轨道发射系统如图13所示，主要由脉冲功率电源、发射器、控制系统和测量系统等四部分组成。脉冲功率电源由22个脉冲成形单元并联构成，单个脉冲成形单元中的电容器电容为5 mF，调波电感为20 μH；发射器采用双匝串联增强结构，初始电感为3 μH，电感梯度为1 μH，初始电阻为0.414 mΩ，电阻梯度为0.112 4 mΩ，电流测量采用罗果夫斯基线圈，出口速度测量采用B-dot磁探针测速法，出口姿态观察采用高速数字摄像机进行拍摄。

由于电磁轨道发射试验可测电参量主要是电流、发射器尾部电压（即整个发射器电压）、出口速度，因此，下面主要通过以上三个电参量对比分析，验发射器仿真模型。

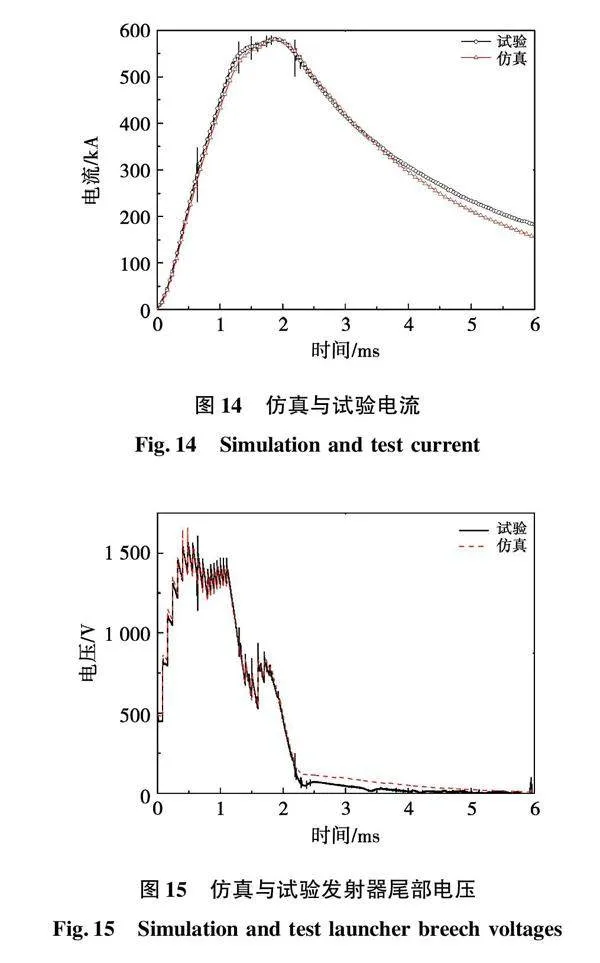
将上述电磁轨道仿真系统按实际试验参数设置并仿真，得到电流和发射器尾部电压仿真与试验波形对比情况如图14和图15所示，采用Spearman相关性分析法，得到的电流和电压相关性系数为0.997 2和0.975 8，仿真与试验电流和发射器尾部电压一致性较好，同时仿真得到出口速度为1 359.2 m/s，与试验测量出口速度1 361 m/s（B-dot）相差较小，验证了电磁轨道发射器仿真模型的正确性。

3 发射器能量转换过程分析

本节将在分析动生阻抗、发射器电阻、发射器电感、枢轨接触电阻等电气负载特性的基础上，研究发射器能量转换规律和过程。

3.1 动生阻抗特性

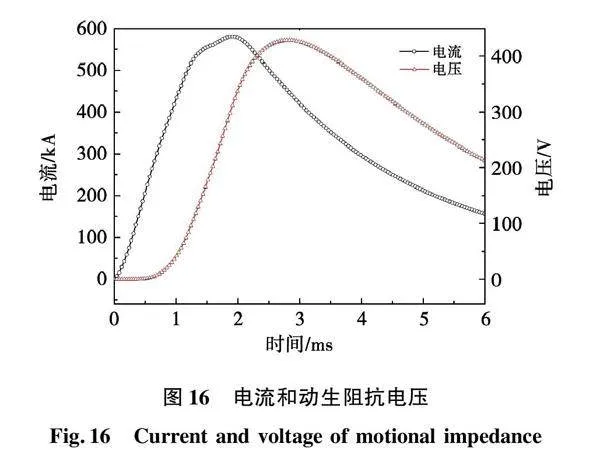
电流和动生阻抗电压波形如图16所示，其电压等于式（2）中的iL′rv。虽然在0～0.26 ms电流从0上升到88.36 kA，但由于发射载荷受摩擦力作用基本处于静止状态，发射载荷速度几乎为零，电压在该阶段也几乎为零。当电流大于88.36 kA时电磁力推动发射载荷加速运动，电压逐渐增加，其峰值428.64 V比电流峰值滞后，原因是动生阻抗电压由电流与速度的乘积决定（假设电感梯度为固定值），当电流达到峰值时，发射载荷速度未达到最大值，两者的乘积不是最大值，随着电流减小和速度增加，在后面某一时刻两者的乘积达到最大值，即该时刻对应的动生阻抗电压最大。因此，动生阻抗电压的峰值出现在电流下降沿阶段，且滞后于电流峰值。

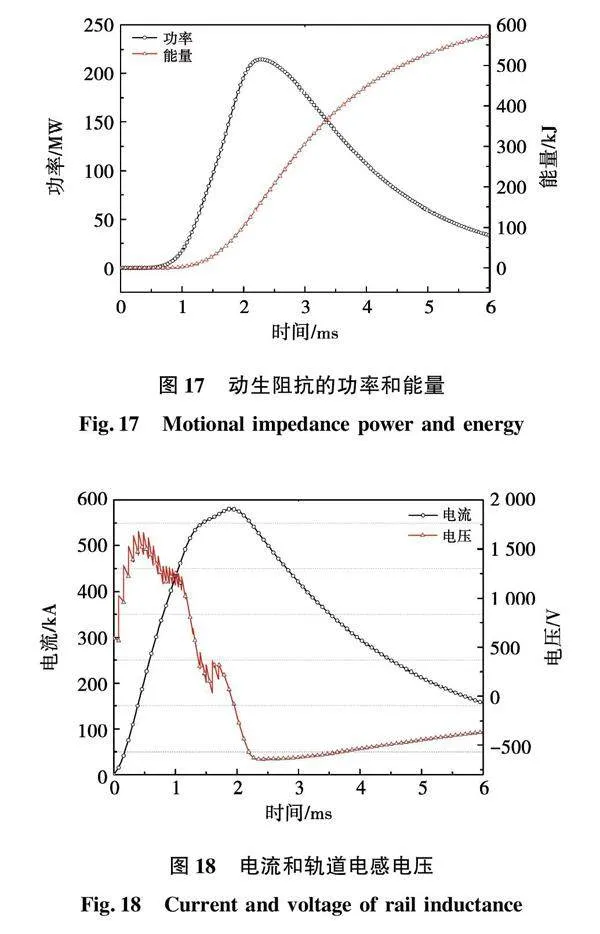
输入动生阻抗的功率和能量随时间变化曲线如图17所示（正值表示输入，吸收能量，负值表示输出，释放能量），功率和能量都是正值说明在整个电磁轨道发射过程中动生阻抗一直在吸收能量，并将其转换为磁能、动能、摩擦热等能量。功率在2.28 ms时达到最大值214.57 MW，最终传输给动生阻抗的能量为573.43 kJ，占输入发射器总能量（812.89 kJ）的70.54%。由前面理论分析可知，其能量一半转换为轨道磁能，一半通过电磁力做功转换为发射载荷动能、摩擦热能和空气动能等能量，通过仿真计算得到发射载荷动能为221.69 kJ，占电磁力做功的77.32%，占输入发射器总能量的27.27%。

3.2 轨道电感特性

电流和轨道电感电压波形如图18所示，轨道电感电压最大值为1 677.46 V，最小值为-639.05 V，轨道电感电压波形前半周为正值，对应电流上升沿，后半周为负值，对应电流下降沿，过零点对应电流峰值，这与轨道电感电压算式（8）相一致，轨道电感电压波形中的波纹是由于脉冲成形单元时序投入系统电路放电引起的。

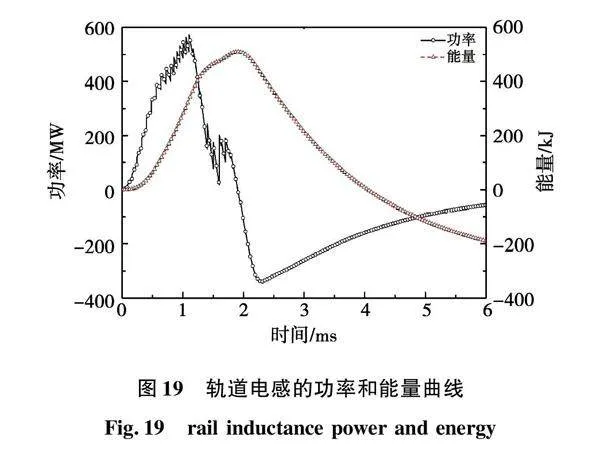
轨道电感的功率和能量随时间变化曲线如图19所示，功率曲线前半周为正值，轨道电感吸收能量磁能增加，最大值为572.01 MW；后半周为负值，轨道电感释放能量磁能减少，最小值为-341.88 MW。能量曲线呈现先增加后减小趋势，最大值为511.11 kJ，在6 ms仿真结束时为-190.03 kJ，说明轨道电感释放的能量大于吸收的能量，这与定值电感吸收与释放能量相等的规律不同。原因是轨道电感中的磁能增加主要有两种方式，一是载流轨道长度增加使轨道电感磁能增加，二是载流轨道电流增大使轨道电感磁能增加，但整个轨道电感磁能减少或释放只能通过轨道电感。因此，通过轨道电感方式释放的能量大于通过轨道电感输入的能量。轨道电感释放的能量比输入的能量多190.03 kJ，而小于输入动生阻抗能量的一半（286.72 kJ），这是由于仿真结束时轨道电感中还有剩余磁能96.69 kJ（对应出口电流为156.40 kA）。

3.3 轨道电阻特性

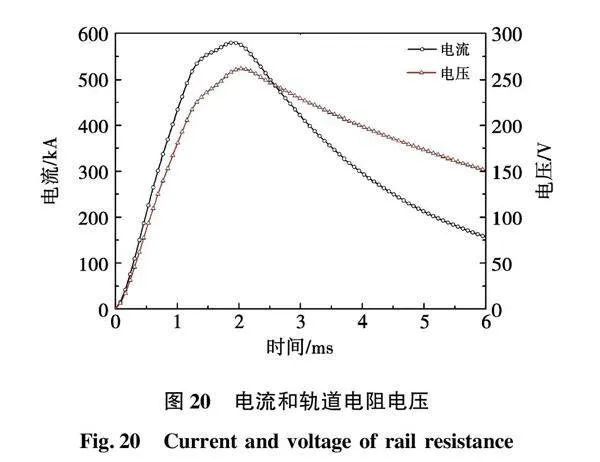
电流和轨道电阻电压波形如图20所示，电压峰值为261.44 V，电压波形变化趋势在前期与电流波形基本一致，后期与电流波形偏差较大。其原因是：由式（9）可知，随着电枢加速运动，馈入电路中的轨道电阻不断增加，其电压与电流比值也不断增大，导致后期轨道电阻电压与电流曲线趋势不一致。

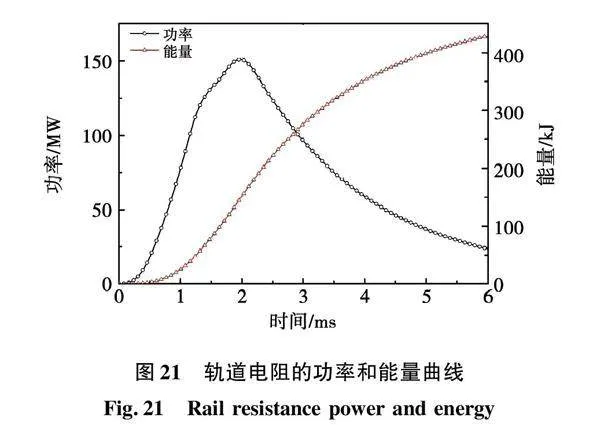
轨道电阻的功率和消耗能量曲线如图21所示，功率呈现先增加后减小的趋势，最大值为150.96 MW，轨道电阻消耗能量（焦耳热）呈逐渐上升趋势，最终消耗能量为428.67 kJ，占输入发射器总能量的52.73%。

3.4 枢轨接触电阻特性

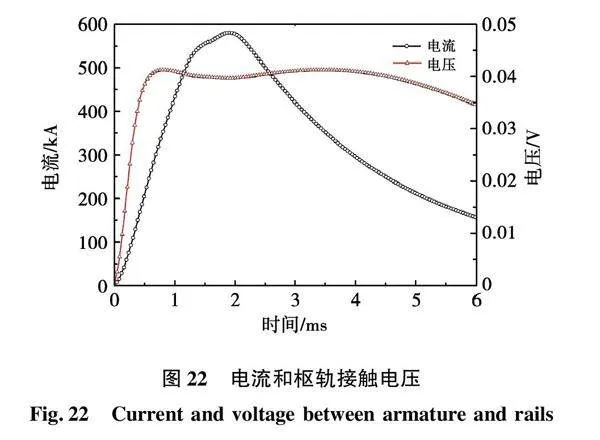
电流和枢轨接触电压波形如图22所示，枢轨接触电压在0～0.76 ms时间内电压迅速从0 V升高至最大值0.041 3 V，随后电压略有微小波动，呈缓慢下降趋势，在出口时刻电流降为156.40 kA，枢轨接触电压为0.034 6 V。

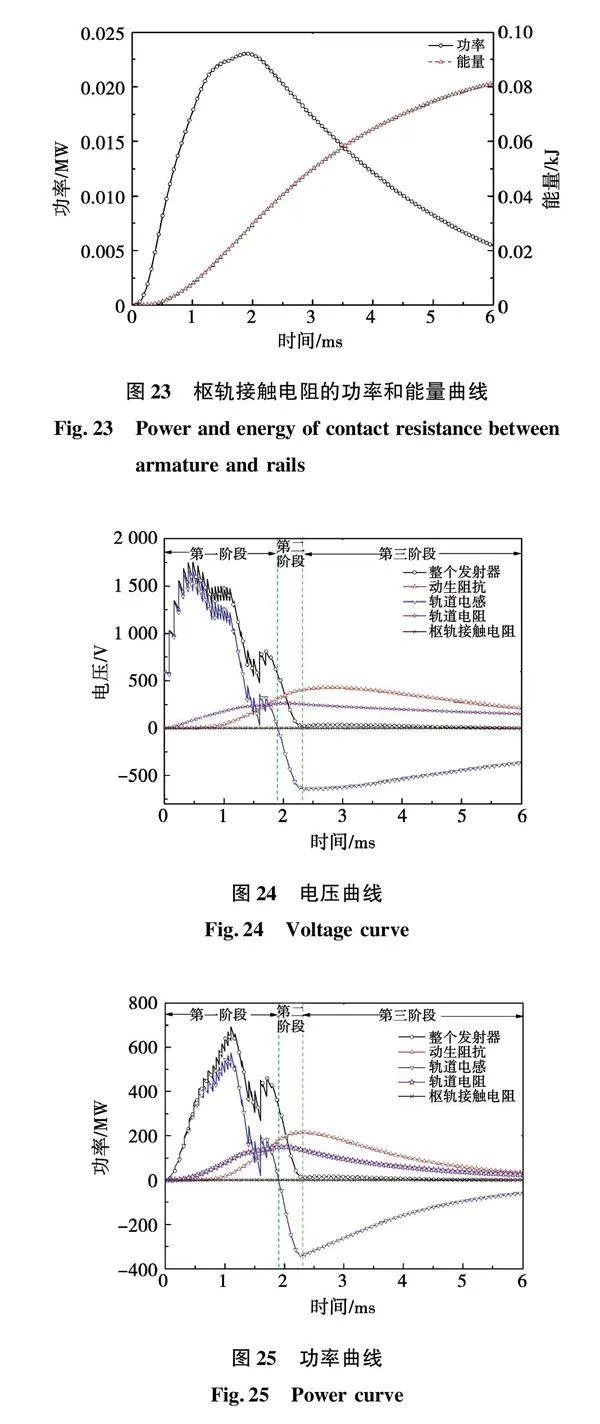
枢轨接触电阻的功率和消耗能量曲线如图23所示，功率呈现先增加后减小的趋势，最大值为0.023 MW，枢轨接触电阻消耗能量（焦耳热）呈逐渐上升趋势，最终消耗能量为0.81 kJ，占输入发射器总能量的0.10%。

3.5 发射器能量转换过程

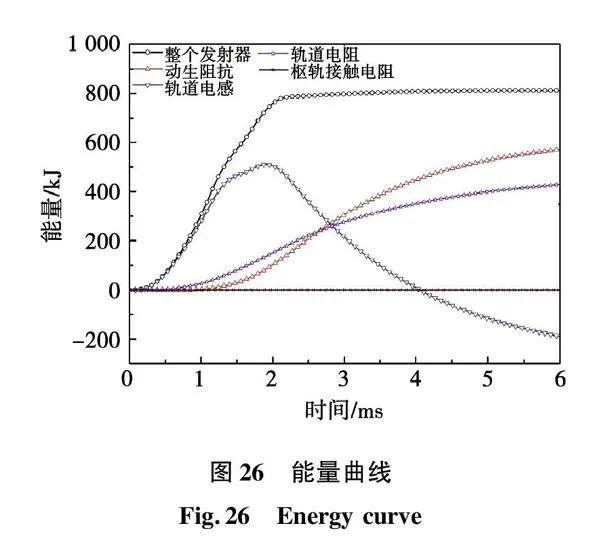
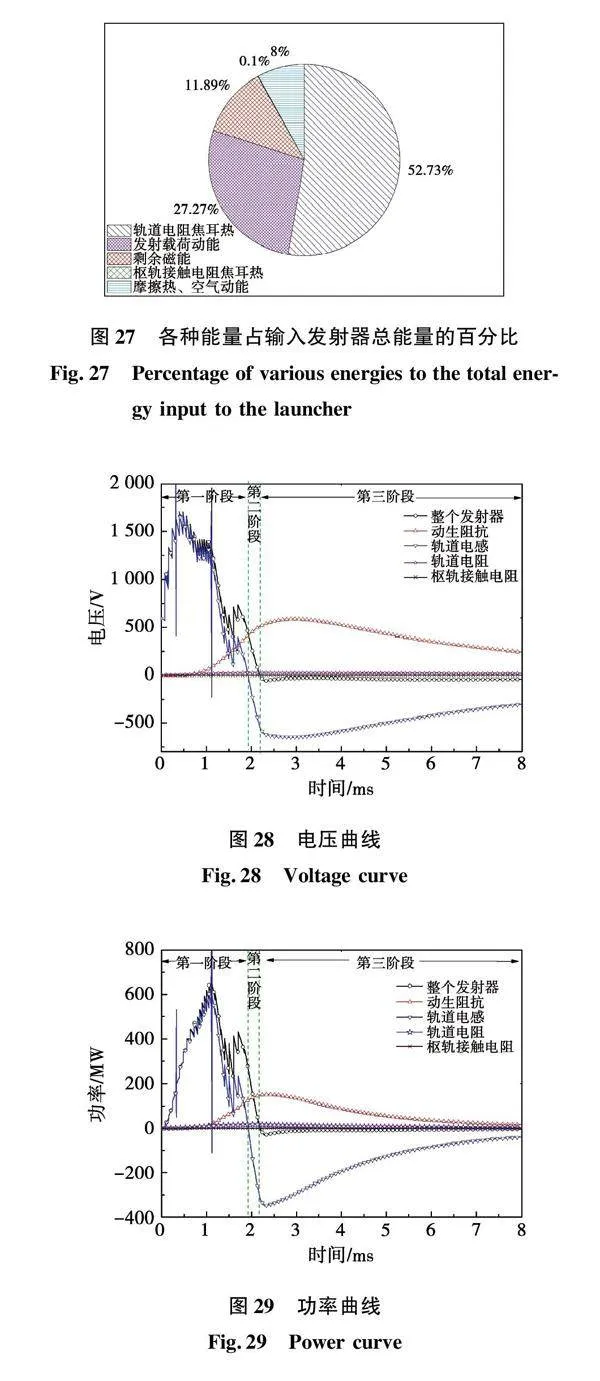
动生阻抗、轨道电感、轨道电阻、枢轨接触电阻和整个发射器的电压、功率、能量随时间的变化曲线如图24、图25和图26所示，整个发射器的电压、功率和能量在整个的电磁轨道发射过程中都是正值，说明脉冲功率电源一直向发射器输入能量，但2.30 ms后电源向发射器输入的能量变得很少。动生阻抗、轨道电阻和枢轨接触电阻电压、功率和能量在整个电磁轨道发射过程中都是正值，说明也一直在吸收能量，并转换为磁能、动能、摩擦热能、焦耳热能等。轨道电感的电压和功率在前半周期为正值后半周期为负值，说明前半周期作为“负载”吸收能量并转换为磁能，后半周期作为“电源”或激励源释放能量，并通过动生阻抗、轨道电阻和枢轨接触电阻转换为磁能、动能、摩擦热能、焦耳热能等。

从“电源”或激励源方式上可将发射器的能量转换过程分为以下三个阶段：第一阶段（0～1.9 ms），脉冲电源作为激励源向发射器输入能量，动生阻抗吸收能量转换为磁能、动能、摩擦热能等，轨道电感吸收能量转换为磁能，轨道电阻和枢轨接触电阻吸收能量转换为焦耳热能；第二阶段（1.9～2.3 ms），脉冲电源和轨道电感共同作为激励源输出能量给动生阻抗、轨道电阻和枢轨接触电阻，动生阻抗吸收能量转换为磁能、动能、摩擦热能等，轨道电阻和枢轨接触电阻吸收能量转换为焦耳热能；第三阶段（2.3～6 ms），轨道电感作为主激励源输出能量给动生阻抗、轨道电阻和枢轨接触电阻，动生阻抗吸收能量转换为磁能、动能、摩擦热能等，轨道电阻和枢轨接触电阻吸收能量转换为焦耳热能。

电磁轨道发射结束时，输入发射器的电能主要转换为轨道电阻焦耳热能、枢轨接触电阻焦耳热、发射器剩余磁能、发射载荷动能、摩擦热能和空气动能等，其中发射载荷动能、摩擦热能和空气动能之和等于电磁力做功，各部分占输入发射器总能量的百分比情况如图27所示，其中轨道电阻消耗能量占比为52.73%，是电磁轨道发射器中消耗能量最多的。

由前面数学模型分析中可知，若将轨道电阻、枢轨接触电阻、摩擦系数等参量降低，减少能量损耗，可提高电磁轨道发射器发射效率。为此，将轨道初始电阻和轨道电阻梯度降至原来的10%，摩擦系数降低为原来的20%，枢轨接触电阻不变，然后进行计算仿真，得到电压、功率和能量曲线如图28、图29和图30所示，与图24、图25和图26的变化趋势相同，都呈现脉冲电源激励、脉冲电源和轨道电感共同激励、轨道电感主激励三个阶段，只是各阶段的转换时刻不同，如整个发射器电压和功率曲线在2.18 ms时刻由正值变为负值，说明发射器由吸收能量转变为向外输出能量，但输出功率很小。

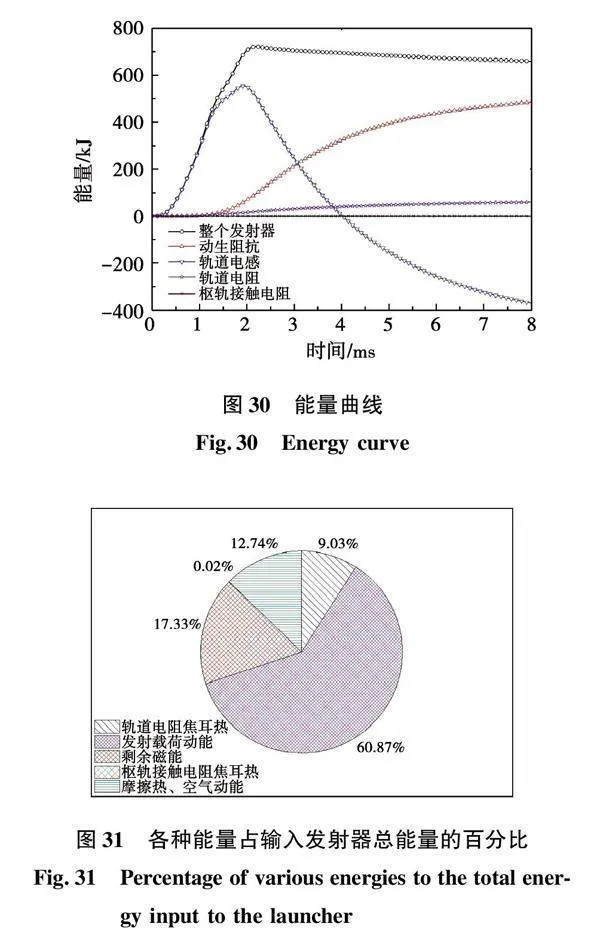
输入发射器的电能转化为轨道电阻焦耳热能、枢轨接触电阻焦耳热、发射器剩余磁能、发射载荷动能、摩擦热能和空气动能等能量的占比情况如图31所示，轨道初始电阻和轨道电阻梯度降至原来的10%，摩擦系数降低为原来的20%后，输入发射器的总能量由812.89 kJ降低为660.25 kJ，发射载荷速度由1 359.2 m/s升至1 830.1 m/s，发射载荷动能由221.69 kJ升至401.92 kJ，占比由27.27%升至60.87%；轨道电阻焦耳热由428.67 kJ降为59.65 kJ，占比由52.73%降为9.03%；发射器剩余磁能由96.69 kJ升至114.34 kJ，占比由11.89%升至17.33%；枢轨接触电阻焦耳热由0.81 kJ降为0.10 kJ，占比由0.10%降为0.02%；摩擦热和空气动能之和由65.03 kJ升至84.14 kJ，占比由8%升至12.74%，这是由于虽然摩擦系数减小了，但发射载荷的位移由原来的4.95 m增加9.98 m，同时由于速度增大空气阻力也成倍增加所致。

4 结 论

1）在电磁轨道发射器简化为动生阻抗、轨道电感、轨道电阻和枢轨接触电阻的基础上，通过其数学模型和计算仿真分析了理想恒流和实际脉冲电流情况下的发射器效率问题，得到实际脉冲电流下发射器效率可突破理想恒流的50%发射效率极限；

2）电磁轨道发射器能量转换过程分为脉冲电源激励、脉冲电源与轨道电感共同激励、轨道电感主激励三个阶段，得到某次典型试验条件下轨道电阻消耗能量占比52.73%最高，将轨道电阻和轨道电阻梯度降为原来的10%，摩擦系数降为原来的20%，轨道电阻消耗能量占比降为9.03%，发射器效率由27.27%提升至60.87%；

3）计算仿真中参数调整是独立变化的，下一步将考虑工程实际参数联动变化情况，开展计算仿真研究，用于指导发射器设计。

参 考 文 献：

［1］王莹，肖峰．电炮原理[M]．北京：国防工业出版社，1995：11-14．

［2］李军，严萍，袁伟群．电磁轨道炮发射技术的发展与现状[J]．高电压技术，2014，40（4）：1052．

LI Jun， YAN Ping， YUAN Weiqun. Electromagnetic gun technology and its development [J]. High Voltage Engineering， 2014， 40（4）： 1052．

［3］马伟明，鲁军勇．电磁发射技术[J]．国防科技大学学报，2016，38（6）：2．

MA Weiming， LU Junyong. Electromagnetic launch technology [J]. Journal of National University of Defense Technology， 2016， 38（6）：2.

［4］马伟明， 鲁军勇. 电磁发射技术的研究现状与挑战 [J]. 电工技术学报， 2023， 38（15）： 3943.

MA Weiming， LU Junyong. Research progress and challenges of electromagnetic launch technology [J]. Transactions of China Electrotechnical Society， 2023， 38（15）： 3943.

［5］陈少辉，成文凭，袁伟群，等．计算焦耳温升作用的电磁轨道发射中电枢尾翼转角处受力分析[J］．高电压技术，2022，48（7）：2762．

CHEN Shaohui， CHENG Wenping， YUAN Weiqun， et al. Stress analysis of the armature tail corner in electromagnetic rail launch after taking joule heating into consideration [J]. High Voltage Engineering， 2022， 48（7）： 2762.

［6］徐伟东，刘峰，袁伟群，等．轨道温度对电磁发射性能的影响[J]．高电压技术，2019，45（9）：3013．

XU Weidong， LIU Feng， YUAN Weiqun， et al. Effect of electromagnetic launch performance under different temperatures of the rails [J]. High Voltage Engineering， 2019， 45（9）： 3013.

［7］袁瑞敏，袁伟群，徐伟东，等．电磁发射中枢轨接触电阻特性研究[J]．电工电能新技术，2018，37（1）：45．

YUAN Ruimin， YUAN Weiqun， XU Weidong， et al. Research on contact resistance characteristics between armature and rails in electromagnetic launch [J]. Advanced Technology of Electrical Engineering and Energy， 2018， 37（1）： 45.

［8］王志增，袁伟群，严萍．瞬态情况下电磁轨道发射器的电感梯度[J]．高电压技术，2017，43（12）：4039．

WANG Zhizeng， YUAN Weiqun， YAN Ping. Inductance gradient for rail-type electromagnetic launcher under transient conditions [J]. High Voltage Engineering， 2017， 43（12）： 4039.

［9］范薇，苏子舟，张涛，等．增强型电磁轨道炮瞬态温升时空分布[J]．高电压技术，2021，47（09）：3346．

FAN Wei， SU Zizhou， ZHANG Tao， et al. Spatial-temporal distribution of transient temperature rise in augmented electromagnetic railgun [J]. High Voltage Engineering， 2021， 47（9）： 3346.

［10］耿轶青，刘辉，马增帅，等．电磁轨道炮枢轨的动态焦尔热特性[J]．高电压技术，2019，45（3）：799．

GENG Yiqing， LIU Hui， MA Zengshuai， et al. Armature and rail’s dynamic joule heating characteristic of the electromagnetic railguns [J]. High Voltage Engineering， 2019， 45（3）： 799.

［11］ENGEL T G， NUNNALLY W C， GAHL J M， et. al. Efficiency and Scaling in DC electromagnetic launchers [C]// 2005 IEEE Pulsed Power Conference， June 13-15， 2005， Monterey， CA， USA. 2005： 249-252.

［12］ENGEL T G， NERI J M， VERACKA M J.The maximum theoretical efficiency of constant inductance gradient electromagnetic launchers [J]. IEEE Transactions on Plasma Science， 2009， 37（4）： 608.

［13］GENG Y， XU L. Analysis of projectile motion in bore and transfer efficiency for electromagnetic railgun [C]// 2010 WASE International Conference on Information Engineering， Aug. 14-15， 2010， Beidaihe， China. 2010：156-160.

［14］SUNG V， ODENDAAL W G.Mathematical analysis of the effects of friction and preacceleration on the efficiency of railguns [J]. IEEE Transactions on Plasma Science， 2019， 47（5）： 2514.

［15］SUNG V， ODENDAAL W G.The effect of changing launch package mass on the electromechanical conversion efficiency of railguns [J]. IEEE Transactions on Plasma Science， 2019， 47（5）： 2521.

［16］LIU S， MIAO H， LIU M.Investigation of the armature contact efficiency in a railgun [J]. IEEE Transactions on Plasma Science， 2019， 47（7）： 3315.

［17］CHANG X， YU X， LIU X， et al.Armature velocity control strategy and system efficiency optimization of railguns [J]. IEEE Transactions on Plasma Science， 2018， 46（10）： 3634.

［18］HUNDERTMARK S， VINCENT G， SIMICIC D， et al. Increasinglaunch Efficiency with the PEGASUS launcher [J]. IEEE Transactions on Plasma Science， 2017， 45（7）： 1607.

［19］CEYLAN D， KEYSAN O. Effect of conducting containment on electromagnetic launcher efficiency [C]// 2017 18th International Symposium on Electromagnetic Fields in Mechatronics， Electrical and Electronic Engineering（ISEF），Sept.14-16，2017，Lodz，Poland.2017： 1-2.

［20］郑杜成，徐蓉，成文凭，等．高速滑动电接触导轨温度场与热应力的仿真分析[J]．电工电能新技术，2019，38（11）：33．

ZHENG Ducheng， XU Rong， CHENG Wenping， et al. Simulation analysis of temperature field and thermal stress of rail in high speed sliding electrical contact system [J]. Advanced Technology of Electrical Engineering and Energy， 2019， 38（11）： 33.

［21］徐蓉，袁伟群，成文凭，等．增强型电磁轨道发射器的电磁场仿真分析[J]．高电压技术，2014，40（4）：1065．

XU Rong， YUAN Weiqun， CHENG Wenping， et al. Simulation and analysis of electromagnetic field for augmented railgun [J]. High Voltage Engineering， 2014， 40（4）： 1065.

［22］符尊靖，徐蓉，徐伟东，等．增强型脉冲大电流直线驱动装置的场路协同仿真[J]．高电压技术，2021，47（10）：3716.

FU Zunjing， XU Rong， XU Weidong， et al. Field-circuit simulation of augmented high pulse current linear drive [J]. High Voltage Engineering， 2021， 47（10）： 3716.

［23］翟小飞， 李鑫航， 刘华， 等. 电磁轨道发射系统电路模型及发射效率研究 [J]. 电工技术学报， 2023， 38（11）： 2841.

ZHAI Xiaofei， LI Xinhang， LIU Hua， et al. Research on circuit model and launch efficiency of electromagnetic rail launch system [J]. Transactions of China Electrotechnical Society， 2023， 38（11）： 2841.

［24］翟小飞， 邹锟， 李配飞， 等. 身管外壳对电磁轨道发射装置发射性能影响分析 [J]. 电工技术学报， 2024， 39（2）： 333.

ZHAI Xiaofei， ZOU Kun， LI Peifei， et al. Analyzing influence of barrel shell on launching performance of electromagnetic rail launcher [J]. Transactions of China Electrotechnical Society， 2024， 39（2）： 333.

［25］蒋启龙，付磊．一种改进型轨道电磁发射方式[J]．西南交通大学学报，2011，46（4）：586．

JIANG Qilong， FU Lei. Improved electromagnetic rail launcher[J].Journal of Southwest Jiaotong University，2011，46（4）：586.

（编辑：刘素菊）

收稿日期： 2023-02-08

基金项目：

作者简介：陈少辉（1980—），男，博士，研究方向为脉冲大电流及电磁发射技术；

王 炅（1982—），男，硕士，工程师，研究方向为电磁发射测控技术；

成文凭（1986—），女，硕士，高级工程师，研究方向为电磁发射结构设计；

严 萍（1965—），女，博士，研究员，博士生导师，研究方向为高电压及脉冲功率技术；

徐伟东（1979—），男，博士，副研究员，研究方向为脉冲大电流放电及应用。

通信作者：徐伟东