数字音频信号处理中的主动降噪方法

牛怡琴

【摘要】本文针对数字音频信号处理中的主动降噪问题展开了研究。首先，通过探讨LMS算法的基本原理，分析了其在降噪任务中的应用及局限性。然后，提出了自适应正则化技术，增强了算法在非平稳噪声环境下的性能和稳定性。最后，利用NOISEX-92数据集对所提出的优化方法进行了实验验证，结果表明优化后的方法在信噪比（SNR）和均方根误差（RMSE）等评价指标上取得了显著的改善，表明自适应正则化技术对提高LMS算法在数字音频信号处理中的主动降噪效果具有重要意义。

【关键词】音频处理；主动降噪；最小均方算法；正则化技术

中图分类号：G212                             文献标识码：A                            DOI：10.12246/j.issn.1673-0348.2024.11.043

数字音频信号处理作为数字信号处理领域中的一个重要分支，在当今社会中扮演着越来越关键的角色[1]。然而，由于传感器本身的特性以及环境噪声等因素的影响，数字音频信号往往会受到不同程度的干扰，从而削弱了信号的质量和清晰度。因此，研究数字音频信号的主动降噪方法对于提升信号处理的效能和性能具有重要的理论和实践价值。

国内外学者们在数字音频信号处理领域开展了大量的研究工作，囊括了传统的降噪方法以及基于机器学习和深度学习的新兴技术。传统的降噪方法主要包括基于统计特性的方法和基于滤波器的方法。其中，最小均方（Least Mean Square，LMS）算法作为一种经典的自适应滤波器算法，被广泛应用于数字音频信号的降噪任务中。然而，传统的LMS算法在处理非平稳噪声时存在收敛速度慢、稳定性差等问题，难以满足实际应用的需求[2]。

本文深入研究了数字音频信号处理中的主动降噪方法。首先，对最小均方主动降噪方法的基本原理进行了探讨。其次，引入自适应正则化技术对LMS算法进行了优化，以期提高其在降噪任务中的性能。最后，采用NOISEX-92数据集对所提出的优化方法进行了测试和评估，验证其在实际应用中的有效性和可行性。通过本文的研究，旨在为数字音频信号处理领域的相关研究和实际应用提供理论指导和技术支持。

1. 最小均方主动降噪方法的基本原理

LMS主动降噪方法是一种经典的自适应滤波器算法，用于数字音频信号处理中的降噪任务。假设有一个长度为N的滤波器w[n]，其输出y[n]与输入信号x[n]之间的关系可以用卷积运算表示：

（1）

其中，w[k]是滤波器的系数（1），n是当前时刻，k是滤波器的时延。LMS算法的目标是通过不断调整滤波器的系数w[k]，使得滤波器的输出y[n]尽可能地接近期望的信号d[n]。因此，LMS算法可以描述为以下迭代更新规则：

（2）

其中，w[n]是滤波器的系数向量，μ是步长参数，e[n]=d[n]-y[n]是估计的误差信号，d[n]是期望的信号。

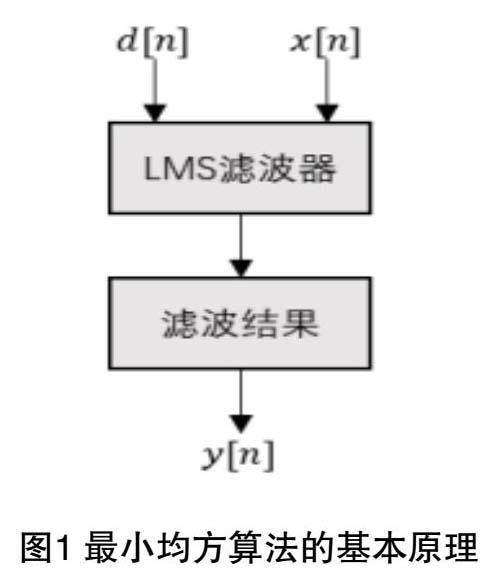
LMS算法的基本思想是不断地根据当前时刻的误差信号来调整滤波器的系数，使得误差信号尽可能地减小。通过这种迭代更新的方式，逐渐使得滤波器收敛到最优解，从而实现了对噪声的有效抑制和信号的恢复，基本流程如图1所示。

图1中，输入信号x[n]和期望信号d[n]分别作为LMS滤波器的输入，经过滤波器后得到输出信号y[n]。然后，通过比较输出信号与期望信号的差异，计算误差信号，并根据LMS算法的更新规则调整滤波器的系数，最终实现主动降噪的效果。

LMS算法的特点主要体现在以下几个方面：首先，LMS算法是一种迭代更新的方法，通过不断地根据误差信号调整滤波器的系数，使其收敛到最优解。其次，LMS算法具有简单易实现、计算量小等优点，适用于实时处理等应用场景。然而，由于其对信号和噪声的统计特性要求较高，当噪声为非平稳时，LMS算法的性能就会受到影响，导致收敛速度较慢或者无法收敛[3]。

为了提高LMS算法在非平稳环境下的性能，引入了自适应正则化技术。自适应正则化技术通过引入正则化项，对LMS算法的更新规则进行优化，从而增强了算法的稳定性和收敛速度。具体而言，自适应正则化技术会根据当前的信号和噪声特性动态调整正则化参数，使其能够在不同的环境下保持较好的性能表现。

2. 基于正则化的最小均方优化方法

自适应正则化技术能够有效地克服传统LMS算法在处理非平稳噪声时的不足，提高了其在实际应用中的适用性和效果。设滤波器的系数为w[n]，输出为y[n]，期望信号为d[n]，则LMS算法的更新规则如式2所示。

为了引入自适应正则化，将LMS算法的目标函数定义为：

（3）

其中，表示期望运算符。

然后，引入正则化项R（w），目标函数变为：

（4）

其中，λ是正则化参数。

常见的正则化项包括L2范数正则化和L1范数正则化，这里以L2范数正则化为例。正则化项R（w）可表示为：

（5）

其中，表示L2范数，即欧几里得范数。

综合以上公式，得到带有自适应正则化的LMS算法更新规则为：

（6）

其中，2λw[n]是对应于L2范数正则化项的梯度下降项。通过这种方式，可以在LMS算法的更新规则中引入自适应正则化，优化算法的性能，提高其在非平稳环境下的适应能力。

在优化之前，传统LMS算法的更新规则只考虑了误差信号与输入信号的乘积，未能充分考虑噪声的统计特性和信号的动态变化，导致在非平稳环境下性能表现不佳。此外，传统LMS算法的参数（如步长参数）需要手动设置，难以适应不同场景下的变化。经过自适应正则化技术的优化后，LMS算法的性能得到了显著改善。首先，引入了正则化项后，可以有效地抑制噪声对滤波器系数的影响，提高了算法的稳定性和鲁棒性。正则化参数的引入使得算法能够自适应地调整滤波器的更新规则，根据当前信号和噪声的特性动态调整步长和正则化程度，从而加速收敛速度并提高抗噪性能[4-5]。此外，自适应正则化技术还能够减少对参数的手动设置，提高了算法的自适应能力。

3. 实验模拟

3.1 数据集与实验方案

在实验部分，本文采用NOISEX-92数据集对方法进行了测试。该数据集是用于音频信号处理领域的一个公认的标准数据集，广泛用于评估降噪算法的性能和效果。该数据集由美国宾夕法尼亚大学（University of Pennsylvania）的研究人员在1992年创建，旨在提供一组包含不同类型噪声的音频信号，以便研究者能够在实验中模拟实际场景下的降噪任务。NOISEX-92数据集包含了来自六个不同环境和来源的噪声样本，涵盖了飞机噪声、城市交通噪声、人声等常见的环境噪声类型[6-7]。这些噪声样本以及与之对应的干净信号也被整理出来，以确保数据的质量和多样性。本文使用该数据集进行实验的方法为：

（1）准备实验环境。在Matlab平台上创建一个新的工程，确保所有必要的工具箱和函数库都已安装和配置。然后，将NOISEX-92数据集导入Matlab环境中，包括噪声样本和相应的干净信号，确保数据格式正确，并进行必要的预处理，包括归一化处理和数据划分。

（2）实现基于LMS算法的主动降噪方法。编写Matlab代码，实现LMS算法的基本原理和自适应正则化优化方法。包括定义滤波器结构、初始化参数、编写主动降噪函数等步骤。

（3）实验设置。根据实验的具体要求，设置合适的参数，包括步长参数、正则化参数等。另外，需要将数据集划分为训练集和测试集，用于模型的训练和评估。

（4）实验训练。利用训练集对实现的主动降噪算法进行训练，即调整滤波器的参数，使其适应于当前的噪声环境和信号特征。在训练过程中，需要监测算法的收敛情况和误差变化，以便及时调整参数和优化算法[8]。

（5）实验评估。利用测试集对训练好的主动降噪算法进行评估，比较输出信号与期望信号之间的差异，评估降噪效果和算法性能。常用的评价指标包括信噪比（Signal-to-Noise Ratio，SNR）、均方根误差（Root Mean Square Error，RMSE）等。

3.2 实验结果与分析

本文用SNR和RMSE对优化前后的方法进行对比和评估，实验结果如表1所示.表1中的SNR和RMSE是两个常用的评价指标，用于评估降噪算法的效果。

从表1中的数据可以看出，在进行了优化后的主动降噪方法中，SNR提高到了18.6 dB，相较于优化前的方法提升了约3.4 dB；同时，RMSE下降到了0.028，相较于优化前的方法降低了0.006。这些数据变化表明，优化后的主动降噪方法在降噪效果和性能上取得了显著的改善。

首先，信噪比（SNR）的提高意味着优化后的方法能够更有效地抑制噪声，并提高信号的质量和清晰度。从实际应用的角度来看，信噪比的增加意味着在同样的信号强度下，信号与噪声之间的区分度更高，使得最终的处理结果更加可靠和准确。其次，均方根误差（RMSE）的降低表明优化后的方法在估计信号与期望信号之间的差异时更加精确，更接近于期望信号的真实情况[9]。这意味着优化后的方法能够更准确地恢复原始信号，降低了信号失真和信息损失的程度，提高了降噪算法的可靠性和稳定性。

整体来说，通过对实验结果的分析，可以明显看出优化后的主动降噪方法相较于优化前具有更优越的性能表现。这一改进不仅提高了信号的质量和清晰度，还增强了算法的稳定性和准确性，为数字音频信号处理领域的实际应用带来了显著的优势和价值。

4. 结束语

本文研究了数字音频信号处理中的主动降噪方法，并以最小均方（LMS）算法为基础，引入了自适应正则化技术进行优化，并采用NOISEX-92数据集对所提出的优化方法进行了实验验证，结果表明优化后的方法在信噪比（SNR）和均方根误差（RMSE）等评价指标上取得了显著的改善。通过对本文内容实验的综合分析可知，自适应正则化技术作为一种优化方法，能够有效地改善传统的LMS算法在处理非平稳噪声时存在的性能不足的问题，能提高其在实际应用中的适用性和效果。本文的研究内容和实验结果充分证明了自适应正则化技术对于提高LMS算法在数字音频信号处理中的主动降噪效果具有重要意义。未来的研究可以进一步探索其他优化方法，并结合实际应用场景，进一步提高降噪算法的性能和适用性。

参考文献：

[1]张毓忠，冷文.数字音频信号处理器理论及专用电路设计[J].电子测量与仪器学报，1994（04）：54-57，62.

[2]陈东，钱光弟.音频信号的数字处理及其应用设计[J].电声技术，2006（02）：22-25.

[3]李伟，汪竹蓉，李晓强，等.数字音频认证研究综述[J].计算机科学，2009，36（10）：21-24.

[4]李忠利，邹会勉，乔冬冬，等.拖拉机驾驶室耳旁噪声主动降噪控制[J].科学技术与工程，2018，18（33）：30-35.

[5]费艳锋，曹祖杨，李坚维.关于主动降噪耳机的研究[J].电声技术，2020，44（05）：38-40，46.

[6]王向阳，牛盼盼.基于音频统计特性的数字水印嵌入算法[J].自动化学报，2008（08）：1001-1003.

[7]张戌宝.现代助听器的降噪技术（单麦克风类）和性能（2）[J].听力学及言语疾病杂志，2014，22（06）：643-645.

[8]徐帆云.基于Matlab的音频降噪滤波器设计[J].电声技术，2017，41（02）：28-33.

[9]陈绍用，徐洋，盛晓伟等.基于滤波最小均方算法的簇绒地毯装备噪声主动控制[J].纺织学报，2020，41（07）：88-92.