“搬家法”构造辅助线解平面几何问题例谈

邹盈欣

摘要：作辅助线来解几何问题是初中数学常用的解题方法，本文中利用“搬家法”的思维来快速构造全等三角形，不仅拓宽了学生的解题思路，而且提高了解题效率.

关键词：辅助线；搬家法；解题方法

通过作出辅助线构造全等三角形是初中几何问题的主要解题方法.很多题目会给出两条线段相等的条件.当给出的两条等线段共顶点、共直线时，学生通常会快速地画出辅助线，构造出全等三角形并成功解题.然而，当给出的两条等线段在图形中相隔距离远，且没有共顶点、共直线时，学生往往没了思路，感觉无从下手，有时会胡乱添加辅助线，反而使图形越来越复杂，解题时间会跟着错误的辅助线一再消耗.此类几何题目可以出现在多种题型中，包括求角度、逆等线、将军饮马、半角模型、三角形旋转等题型.

在解答这类两条等线段条件的几何题目时，笔者总结出一种创新思考方法——“搬家法”，其本质就是将以其中一条等线段为边的三角形“搬家”到另一条等线段上，搬家过去的三角形自然是全等，进而快速解决问题.当然，当已知两条等线段有连接要素，包括共顶点、共直线时，也可以使用“搬家法”构造全等.

“搬家法”可以大幅减少学生的思考时间，掌握“搬家法”思维，学生可以快速构造辅助线，提高解题效率.

下面以几种经典模型为例来介绍“搬家法”的应用.

1 半角模型和旋转例题

例1如图1，正方形ABCD中，BM和DN分别是正方形两个外角的平分线，且∠MAN=45°，求证：BM2+DN2=MN2.

分析：这道题的常规思路是发现已知条件中的半角模型，再联想旋转构造全等.这个思路对学生的模型掌握、思维能力都有一定的要求.“搬家法”思路如下：

图中标有共同顶点A的三角形共有△ABM，△ADN，△AMN三个，其中△ABM，△ADN中有AD，AB两条等线段.那么将以AD为一边的△ADN搬家去AB边上，或将以AB为一边的△ABM搬家去AD边上，分别得到图2和图3.

“搬家”后的三角形自然是全等的，即图2中的△ADN≌△ABN′，图3中的△ABM≌△ADM′.分别连接MN′，M′N后，学生也不难观察到图2中△AMN≌△AMN′（SAS），图3中△AMN≌△AM′N（SAS），进而观察到所需求证的三条线段BM，DN及MN分别等量代换成图2中△BMN′中的BM，BN′及MN′和图3中△DM′N中的DM′，DN及M′N.

在图2中，由已知条件可得∠ABN′=∠ADN=∠ABM=90°+45°=135°，所以∠MBN′=90°.在Rt△BMN′中，由勾股定理证得BM2+BN′2=MN2.

在图3中，由已知条件可得∠ADM′=∠ABM=∠ADN=90°+45°=135°，所以∠M′DN=90°.在Rt△M′DN中，由勾股定理证得DN2+DM′2=M′N2.

故可证明BM2+DN2=MN2.

2 求角度例题

例2如图4，等腰三角形ABC中，AB=AC.∠A=20°.AD=BC.求∠CDB的度数.

分析：本题作为经典考题，给出的关键条件是AD=BC.而AD，BC这两条等线段没有关联点.网络教学视频给出了大量不同思路的讲解，辅助线的构造方法更是层出不穷，但都没有讲解究竟怎样才能让学生想到构造辅助线.通过“搬家法”，学生可以基本无需思考即可作出多种辅助线.

“搬家法”思路如下：

观察以这两条等线段AD，BC为边的三角形有△ADC，△ABC和△BCD.将以AD为一边的三角形搬家到BC边上，或将以BC为一边的三角形搬家到AD边上，即可作出辅助线.

如将以AD为一边的△ADC搬家到另一条等线段BC上，得到图5和图6.

图5中，由于“搬家”后的三角形是全等的，学生也不难观察到△BCC′≌△DAC，所以∠BCC′=20°，CC′=AC.由已知条件可得∠ABC=∠ACB=80°，则∠ACC′=60°.连接AC′后可得等边三角形ACC′及等腰三角形ABC′，所以∠BAC′=∠CAC′-∠CAB=40°.在等腰三角形ABC′求得∠ABC′=∠AC′B=70°，所以∠ACD=∠CC′B=∠AC′B-∠AC′C=70°-60°=10°.故∠CDB=∠ACD+∠BAC=20°+10°=30°.

图6中，△BCC′≌△ADC.连接AC′后可得等边三角形ABC′及等腰三角形ACC′，进而观察到含有60°的等腰三角形ACC′及三角形ABC′.通过等边三角形的角轻松求出答案.

同样的搬家道理，也可以将以BC为一边的△ABC搬家到另一条等线段AD上，得到图7.“搬家”后得到△ABC≌△A′AD.学生同样很容易连接CA′得到等边三角形AA′C，进而求出答案.

例3如图8，AB=AD=BC，∠ABC=90°，∠BAD=30°，求∠C的度数

分析：此题常规解题思路是以AB，BC为边补齐正方形，通过对角线性质再求解.对于八年级上学期的学生来说很难求解，但连接BD后，通过“搬家法”也可以轻松求解.连接BD后，由已知的重要条件AB=AD=BC来观察这三条等线段上的三角形只有△ABD和△BDC.“搬家法”的思路是把△BCD搬到AB边上（如图9），或是把△ABD搬到BC边上（如图10和图11）.

在图9中，由已知条件得到∠ABD=∠ADB=75°，∠CBD=90°-75°=15°.把△BCD搬到AB边上，则△BCD≌△BAD′，于是得到∠BAD′=∠BCD，∠ABD′=∠CBD，BD=BD′.故∠ABD′=∠CBD=15°，那么∠DBD′=60°，随即得到△BDD′为等边三角形，即BD=BD′=DD′.所以△ABD′≌△ADD′（SSS），于是∠BAD′=∠DAD′.又已知∠BAD′+∠DAD′=30°，所以∠BCD=∠BAD′=15°.

在图10中，由已知条件得到∠ABD=∠ADB=75°，∠CBD=90°-75°=15°.把△ABD按图10搬到BC边上后，△ABD≌△BCD′，∠CBD′=∠BAD=30°，所以∠DBD′=∠CBD′-∠CBD=15°，∠ABD′=90°-30°=60°，所以△ABD′为等边三角形.随即得到AF为等边三角形△ABD′的BD′边上的三线合一的中线.再过点D作BC的垂线，垂足为E，不难证明△BDE≌△BDF（AAS），则有BE=BF=12BD′=12BC，所以CE=BC-BE=12BC，从而△BCD为等腰三角形，故∠BCD=∠CBD=15°.

在图11中，由已知条件得到∠ABD=∠ADB=75°，∠CBD=90°-75°=15°.把△ABD按图11搬到BC边上后，△ABD≌△BCD′.由∠ABD′=90°+30°=120°，∠A=30°，AB=BD′，可证A，D，D′三点共线，且△ABD′为等腰三角形.通过角度计算，可得∠DBD′=∠CD′D=45°.看到45°角学生自然会联想到作高，分别过点C，D作AD′和BD′的高，垂足分别为E，F，从而证得△BFD≌△CED′.所以DF=CE.在Rt△DFD′中，因为∠DD′F=30°，所以DF=12DD′，所以CE=12DD′，从而证得∠DCE=45°，故∠DCB=∠DCE-∠BCE=∠DCE-（∠BCD′-∠ECD′）=15°.

3 逆等线将军饮马例题

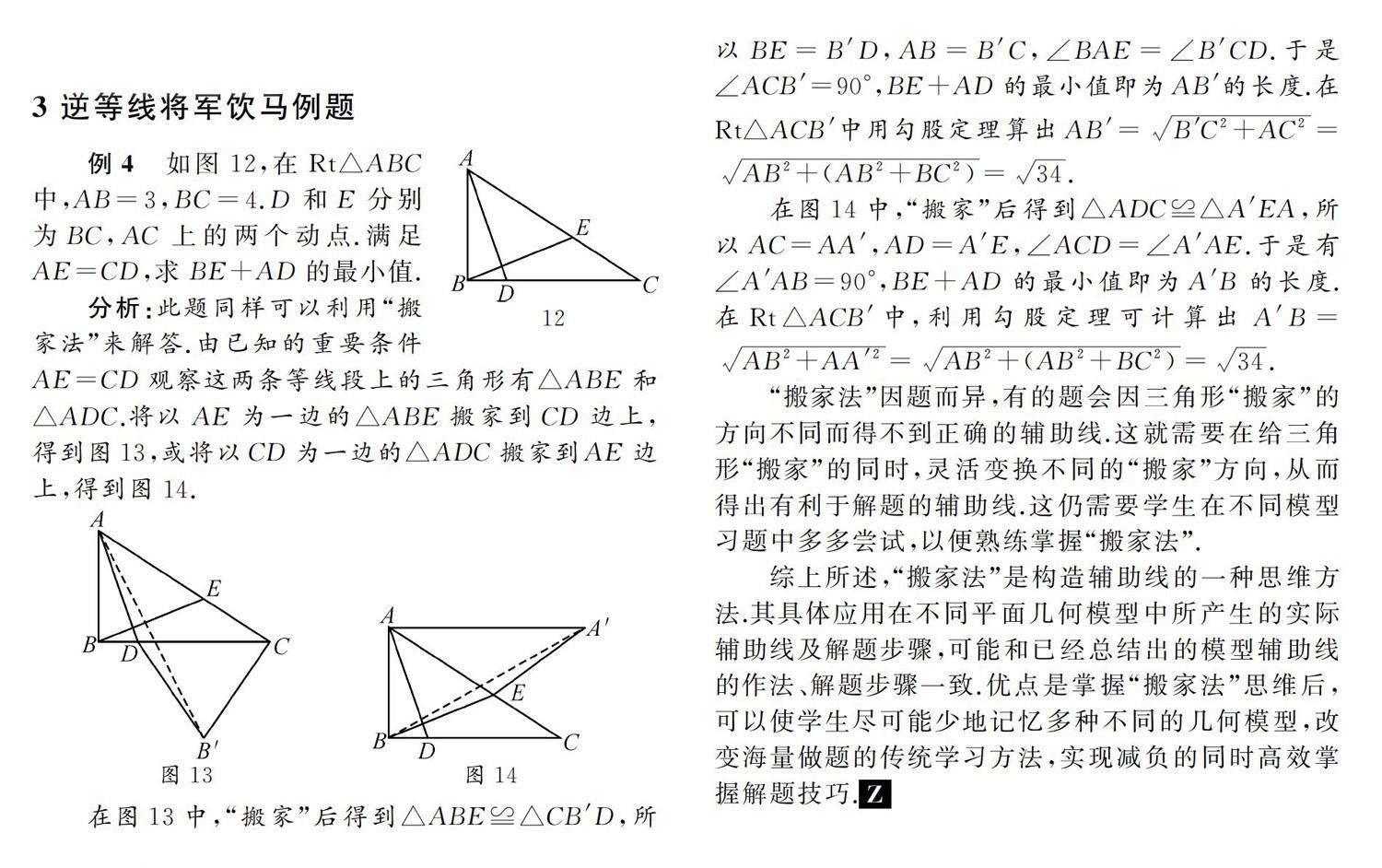
例4如图12，在Rt△ABC中，AB=3，BC=4.D和E分别为BC，AC上的两个动点.满足AE=CD，求BE+AD的最小值.

分析：此题同样可以利用“搬家法”来解答.由已知的重要条件AE=CD观察这两条等线段上的三角形有△ABE和△ADC.将以AE为一边的△ABE搬家到CD边上，得到图13，或将以CD为一边的△ADC搬家到AE边上，得到图14.

在图13中，“搬家”后得到△ABE≌△CB′D，所以BE=B′D，AB=B′C，∠BAE=∠B′CD.于是∠ACB′=90°，BE+AD的最小值即为AB′的长度.在Rt△ACB′中用勾股定理算出AB′=B′C2+AC2=AB2+（AB2+BC2）=34.

在图14中，“搬家”后得到△ADC≌△A′EA，所以AC=AA′，AD=A′E，∠ACD=∠A′AE.于是有∠A′AB=90°，BE+AD的最小值即为A′B的长度.在Rt△ACB′中，利用勾股定理可计算出A′B=AB2+AA′2=AB2+（AB2+BC2）=34.

“搬家法”因题而异，有的题会因三角形“搬家”的方向不同而得不到正确的辅助线.这就需要在给三角形“搬家”的同时，灵活变换不同的“搬家”方向，从而得出有利于解题的辅助线.这仍需要学生在不同模型习题中多多尝试，以便熟练掌握“搬家法”.

综上所述，“搬家法”是构造辅助线的一种思维方法.其具体应用在不同平面几何模型中所产生的实际辅助线及解题步骤，可能和已经总结出的模型辅助线的作法、解题步骤一致.优点是掌握“搬家法”思维后，可以使学生尽可能少地记忆多种不同的几何模型，改变海量做题的传统学习方法，实现减负的同时高效掌握解题技巧.