核心素养下的高三数学大单元复习设计研究

黄文芳

［摘 要］文章结合“解三角形”大单元复习，探索核心素养下的高三数学大单元复习设计，旨在通过大单元复习进一步引导学生完善知识体系，发展学生思维，培养学生能力。

［关键词］核心素养；高三数学；大单元复习

［中图分类号］    G633.6        ［文献标识码］    A        ［文章编号］    1674-6058（2024）08-0005-04

从近五年高考数学试卷的研究与分析情况来看，为推进学生核心素养的发展，落实立德树人根本任务，高考数学试题依据学生的学习内容和学习能力进行相应的情境设置，考查学生对学科知识的掌握情况，同时注重体现开放性、灵活性和探究性，强调学用结合，考查学生的逻辑思维能力以及计算能力。基于此，增强学科教学整合与高考的衔接，落实大单元教学，培养学生的思维能力，是当前高中数学教学的追求。

核心素养下的大单元教学是围绕立德树人根本任务进行的。在大单元教学中，教师要依据单元知识以及单元教学方法之间的联系，对数学教材进行细致的分析与研究，并对从中提取到的数学信息进行解析、整理以及重构。

高三数学一轮复习重在“复”，但不是“穿旧鞋走老路”，而是要在清晰明朗的逻辑主线下，对已有知识、经验进行重组与深化，形成整体的“经验单元”。为此，高三数学复习课教学应从整体着眼，以单元教学为基本形式。

本文以人教A版高中数学必修第二册的“解三角形”单元复习为例，进行深入的研究与分析，并从中获取相应的教学信息，促使学生在数学单元复习中实现数学学科核心素养的提升。

一、教学设计

（一）回顾与重构

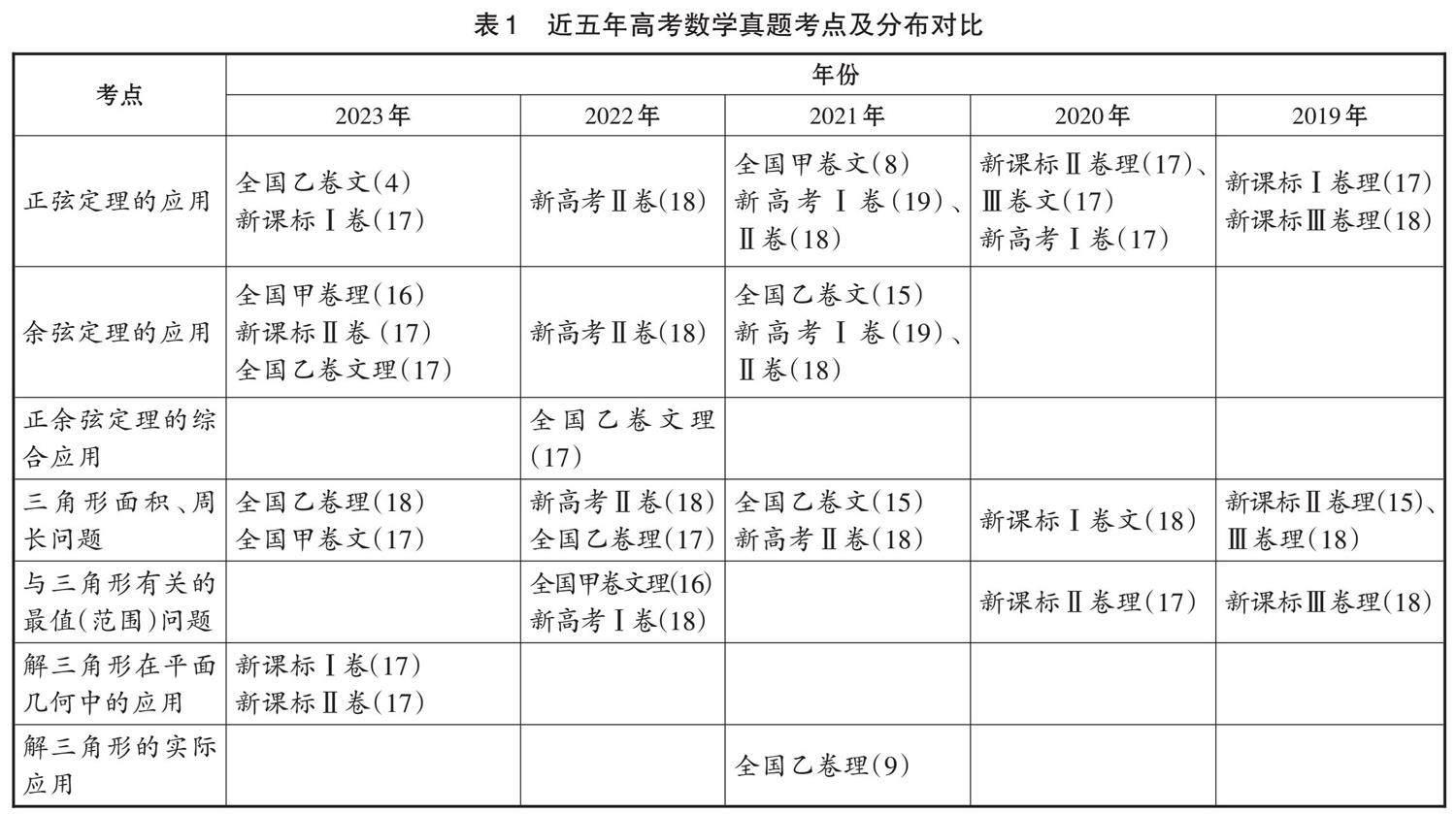
活动1：收集近五年高考数学真题考点（以全国卷为主），见表1。

设计意图：一轮复习既要重视教材，又要关注高考真题。通过真题分类汇编，让学生了解知识点及考点。

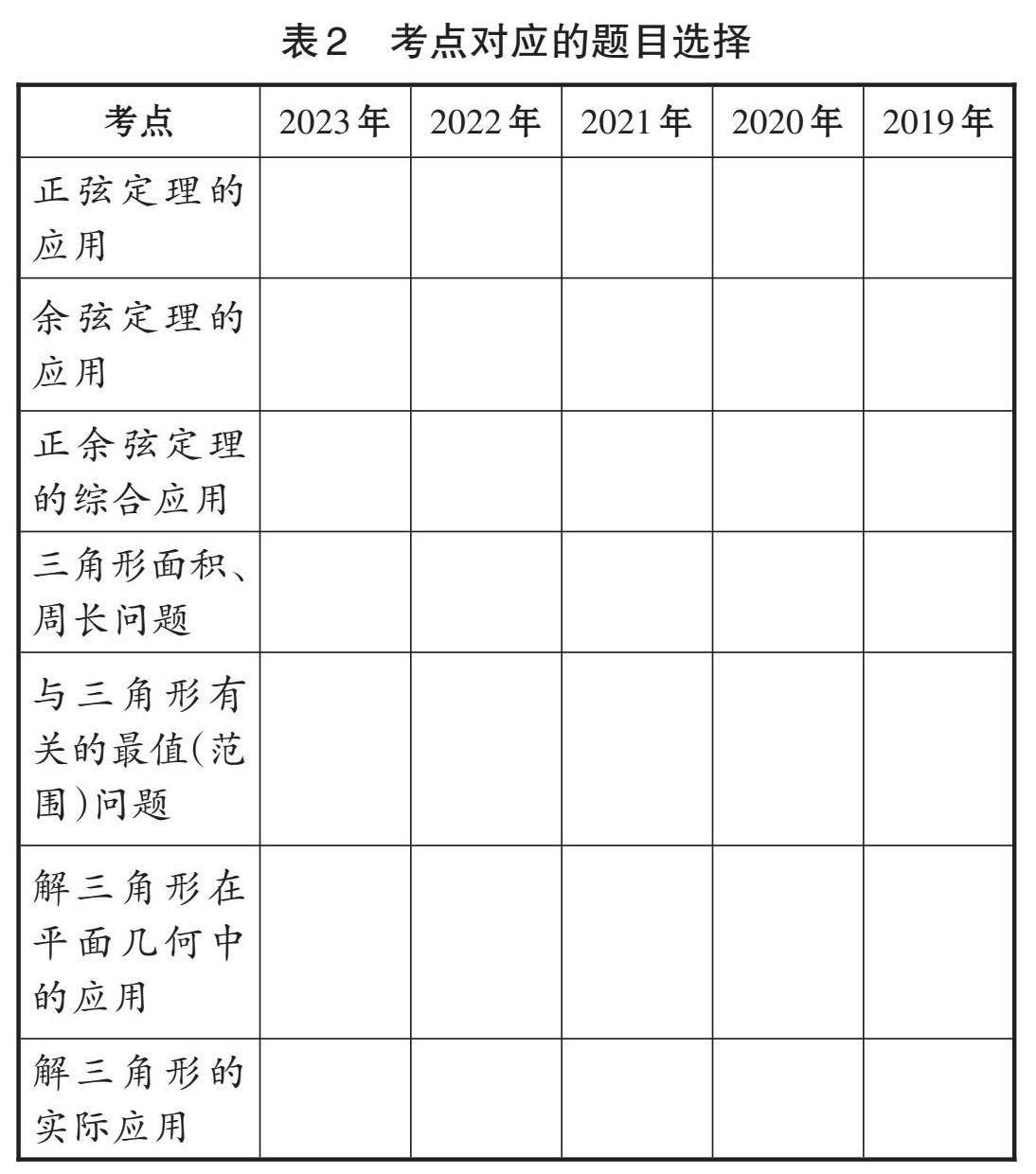
活动2：自主填表（见表2），对每一个考点选择一道题进行说明。

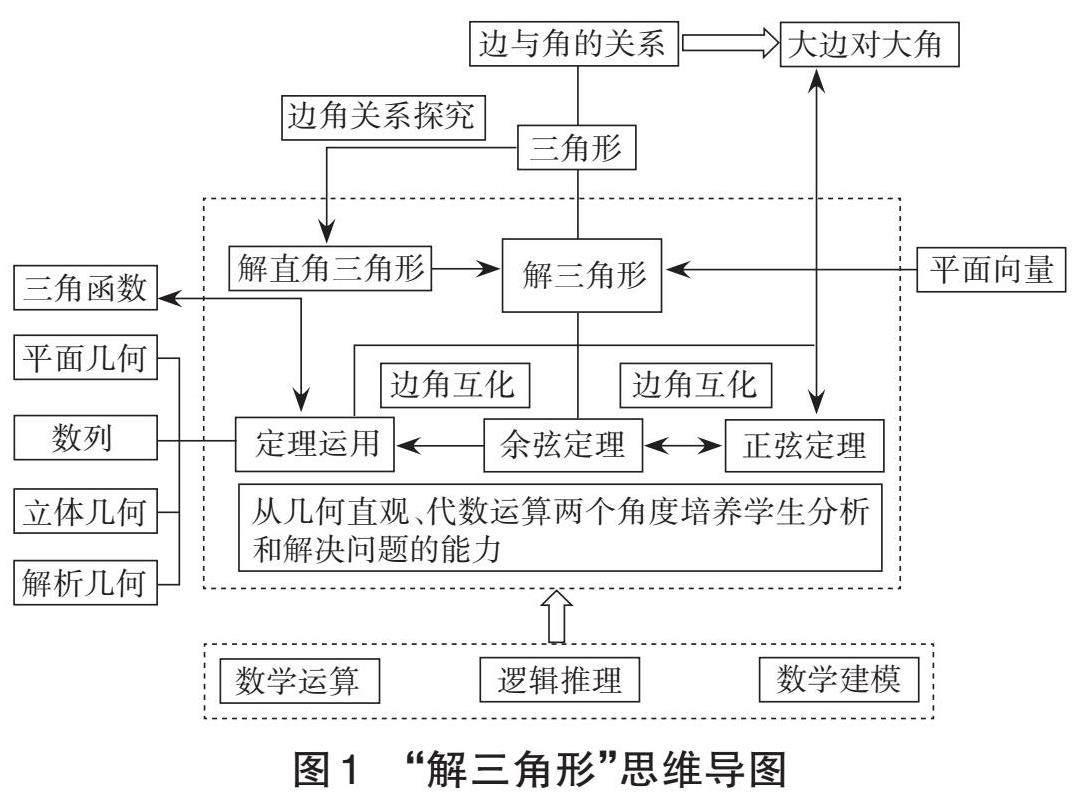
活动3：试绘制“解三角形”思维导图（构建知识框架）。

设计意图：活动1通过研究高考真题的考点，明确复习的方向和思路；活动2通过试题与“四基”对接，完美融合知识与能力，选取的题目可助力学生理解知识，而知识的理解又可助力学生解题能力的提升，从而形成良性循环；活动3的复习核心目标是帮助学生梳理并整合基础知识，构建知识体系，最终提升其解题能力，培养其数学素养。这些活动拟在课前让学生自主完成，课堂上教师再根据学生的完成情况进行针对性讲评。

（二）应用与串联

问题1：为什么要以“解三角形”为一个单元进行复习？

设计意图：在梳理单元思维导图、近五年全国卷的高考题、教材必修第二册出现的部分例题和习题的基础上，让学生思考问题，由此认识以“解三角形”为一个单元进行复习的重要性和必要性。

问题2：主要研究什么？如何研究？

设计意图：从学生已有的知识结构和活动经验出发，给出之前复习解三角形时绘制的思维导图（如图1），这个思维导图就是本节课复习活动组织的逻辑主线，起到先行组织者的作用。由此让学生了解本节课的研究流程：问题引领—正余弦定理—定理应用。

问题3：[△ABC]的内角[A、B、C]所对的边分别为[a、b、c]，已知[sinB（acosB+bcosA）=3ccosB]。（1）角[B]的值；（2）若[b=23]，[△ABC]的面积为[23]，求[△ABC]的周长。

设计意图：本题属于基础题，解答过程需应用正弦定理、余弦定理、三角形面积公式、三角形内角和定理等知识。教师可以在讲解题目的过程中适时引导学生回顾复习相关知识点，以达到回顾复习、梳理整合知识的目的。

变式1（串联降幂公式）：[△ABC]的内角A、B、C所对的边分别为[a、b、c]，已知[sinB（acosB+bcosA）=23ccos2B2-3]，求[B]。

变式2（串联同角三角函数的基本关系）：[△ABC]的内角A、B、C所对的边分别为[a、b、c]，已知[2sinBtanB=3]，求[B]。

变式3（串联重要不等式）：[△ABC]的内角A、B、C所对的边分别为[a、b、c]，已知[B=60°]，[b=23]，求[△ABC]面积的最大值。

变式4（串联三角公式）：[△ABC]的内角A、B、C所对的边分别为[a、b、c]，已知[3sinB（acosB+bcosA）=ccosB+c]，求[B]。

变式5（串联平面几何知识）：[△ABC]的内角[A、B、C]所对的边分别为[a、b、c]，已知[B=60°]，[△ABC]外接圆的面积为[4π]，求[△ABC]周长的最大值。

变式6（串联数列、基本不等式）：[△ABC]的内角[A、B、C]所对的边分别为[a、b、c]，已知[B=60°]，[a+c=4]，（1）当[a、b、c]成等差数列时，求[△ABC]的面积；（2）设[D]为[AC]的中点，求线段[BD]长的最小值。

设计意图：通过6个变式，使学生进一步巩固定理，把握各个知识点的联系，构建完整的知识网络；通过问题的解答，提升学生解决问题的能力。

（三）小结与反思

1.本节课我们研究了解三角形的哪些内容？如何研究？解三角形有哪些应用？

2.今后遇到解三角形的问题，你可以从哪些方面进行研究？如何研究？

二、教学成果

（一）用思维导图完善知识体系

要想有效复习“解三角形”这个单元的内容，教师应结合学生的具体情况，以三角函数与解三角形两个重点内容为基础，引导学生绘制思维导图（如图2）；结合相应的图表、知识框图等将三角函数、解三角形的有关知识进行归纳整理，帮助学生完善自己的数学知识体系。

（二）创设情境，利用信息技术，提升数据分析能力

在“解三角形”单元复习教学中，教师应创设情境引导学生进行复习，激发学生的复习兴趣。教师可结合学生已学的数学知识，引入实际生活中的例子，引导学生对其进行分析。在分析过程中，除了要有文字的表述，教师还可利用信息技术，如视频软件、GGB软件等，将一些动态的变化过程可视化（如图3），助力学生分析与解决问题，提升学生的数据分析能力。

（三）归类变式，强化知识应用

在“解三角形”单元复习中，待学生对相关基础知识有了一定的积累后，教师可以结合学生已学的知识引导学生进行相应的习题变式训练。通过习题变式训练，让学生对相关问题有更深入的理解，提升学生的知识应用能力。

［例题］在等腰[△ABC]中，[AB=AC]，[D]是线段[AC]的中点，[BD=a]为定长，求[△ABC]面积的最大值。

变式1：在等腰[△ABC]中，[AB=AC]，[D]是线段[AC]的中点，[BD=a]为定长，求[△ABC]面积的最值。

变式2：在等腰[△ABC]中，[AB=AC]，内角[B]的平分线交[AC]于点[D]，[BD=a]为定长，求[△ABC]面积的最值。

在原题的基础上，改变其中某个条件或者某些已知条件，改变题目呈现的形式和提问方式，将具体的数值变为字母参数等，引发学生思考。结合问题对学生进行追问：通过这些变式训练，你发现了什么规律？通过变式训练，引导学生思考问题，有助于学生实现对所学三角函数、解三角形、平面几何及数列等有关知识的迁移和应用，提升学生的思维水平，培养学生的解题能力。

（四）改善评价，优化教学，提高核心素养

对学生实施科学合理的学习评价是数学教学实践的重要环节。对学生实施科学合理的学习评价，不仅能为教师提供教学反馈，还有助于教师结合反馈情况改进教学。教师要改变以往单一的教学评价方式，积极优化教学评价方式，改善评价内容。从“解三角形”单元复习的综合分析来看，本次课程的复习内容具有递进性、科学性以及结构化的特点。因此，教师在对学生的学习表现进行评价时，要依据学生不同的学习阶段制定不同的评价标准，运用多元化的评价方式。通过评价，让学生的核心素养获得一定的提升。

三、评价反思

在核心素养下引导学生进行数学单元复习，教师要对数学教材进行细致的研究与分析，以教材为基础，结合相应的例题，为学生提供相应的复习引导，促使学生能够深入理解知识并灵活运用知识，能够发现知识的本质规律。教师要摒弃题海战术，通过变式训练启发学生思维；要坚持以学生为主体，在课堂上给学生创设自主学习的空间，推动学生数学学科核心素养的发展。通过大单元教学的实施，教师可以提升自身的专业素养和教学能力。教师应基于核心素养开展大单元复习教学，探索数学教学之道，提高教学效能。

［   参   考   文   献   ］

［1］  中华人民共和国教育部.普通高中数学课程标准：2017年版2020年修订［M］.北京：人民教育出版社，2020.

［2］  教育部考试中心.中国高考评价体系说明［M］.北京：人民教育出版社，2019.

［3］  中国高考报告学术委员会.中国高考报告（2023）［M］.北京： 新华出版社，2023.

［4］  丁益民.深度学习视域下高中数学单元教学设计与实践［M］.哈尔滨：哈尔滨工业大学出版社，2022.

（责任编辑 黄桂坚）