基于网格聚类优化的区域热点路径识别

翁旭艳 郑淑妮

摘要：针对轨迹聚类方法难以准确识别高相似热点路径的问题，提出能区分起讫点或局部路段的热点路径识别方法，将出行轨迹映射并压缩为移动网格序列，分别从边界与内部区分序列间的空间相似性度量，整合转化为距离并进行基于方格序列密度的空间聚类（grid sequencedensity-based spatial clustering of applications with noise，GS-DBSCAN）。以青岛市市南区部分出租车的轨迹数据为例，与只考虑内部相似性且分别以对比序列中较短序列和较长序列为基准的聚类方法进行对比验证。结果表明：同时考虑边界与内部相似性且以较长序列为基准的GS-DBSCAN算法能正确区分多出行起讫点分布下长度差异较大的分离、汇合与交叉耦合热点路径，受路径长度、网格尺寸等变量差异的影响小于2%，且聚类运算效率较高。

关键词：热点路径；边界；内部；轨迹聚类

中图分类号：U491文献标志码：A文章编号：1672-0032（2024）02-0089-08

引用格式：翁旭艳，郑淑妮.基于网格聚类优化的区域热点路径识别［J］.山东交通学院学报，2024，32（2）：89-96.

WENG Xuyan， ZHENG Shuni. Regional hotspot path identification based on grid clustering optimization［J］.Journal of Shandong Jiaotong University，2024，32（2）：89-96.

0 引言

在交通领域广泛应用全球定位系统（global positioning system，GPS），可得到大量车辆轨迹数据，为车辆路径规划、交通运行等研究提供数据支持。Wang等[1]、Zhang等[2]通过出租车轨迹GPS数据检测车辆异常轨迹；Liu等[3]、陈振华[4]通过出租车GPS轨迹数据分析城市交通拥堵模式；Lin等[5]通过GPS轨迹数据预测城市交通路网流量。通过GPS轨迹数据分析热点路径的研究较多，热点路径指在一段时间内车辆频繁经过的路段，通过识别热点路径，可为绿波带设置、主路优先等交通运行管理提供决策依据。采用聚类方法识别热点路径的关键是相似性度量[6]。李颖等[7]分别采用离散弗雷歇算法、动态时间规整算法、最长公共序列（longest common subsequence，LCS）算法和实序列编辑距离算法对货车轨迹数据进行聚类，认为LCS算法的有效性最优。Kim等[8]以LCS算法下车辆行驶距离与较短轨迹距离之比作为轨迹空间相似度进行基于密度的聚类（density-based spatial clustering of application with noise，DBSCAN）算法，分析交通网络中空间和时间出行模式。冯琦森[9]、赵欣[10]改进DBSCAN算法，前者结合重庆地形特点考虑海拔高度因素，认为比对轨迹中的最大海拔高度差不应超过一定范围，否则相似度为0；后者在轨迹点空间相似度度量上增加车辆转角差异性，定义时间维度上的轨迹相似度。Kang等[11]通过直接度量轨迹网格序列间重叠区域表征轨迹相似性。吴俊伟等[12]将网格抽象为图模型并通过图搜索进行网格聚类。王超[13]考虑时空事件的密度和类型对出租车轨迹点进行聚类。Lee等[14]提出基于轨迹分段的相似性度量，对速度或方向上快速变化的轨迹点分段。在轨迹映射至网格空间的聚类研究中，可通过直接度量轨迹网格序列间重叠区域表征轨迹相似性[15]，也可将网格抽象为图，以邻接网格的共有轨迹定义网格间可达性，通过图搜索进行网格聚类及热点路径识别[16]。通过优化相似度算法、增加相关因素变量等全面、准确地分析轨迹数据，但以较短轨迹为基准的LCS相似度可能造成过于重视不同热点路径的重叠部分，导致将重叠度较高的不同路径归为同一类热点路径。起讫点（origin-destination，OD）矩阵和路径流量的研究较多，但考虑轨迹数据的边界起讫点和内部中间点属性的研究较少。双层规划模型[17]在OD矩阵估计中应用较多，Ou等[18]基于机器学习算法，提出估计动态OD流量的双层框架；Tang等[19]将改进的三维卷积神经网络模型用于动态OD矩阵估计；Cao等[20-21]提出的OD矩阵，采用极大似然法拟合各路段的速度-密度函数，建立基于动态交通分配的双层广义最小二乘法估计器，分析浮动车采样频率较低时的OD矩阵估计方法，保证正常估计路段流量；Huang等[22]采用长短期记忆（long short-term memory，LSTM）模型估计OD矩阵。以较短轨迹为基准的LCS相似度识别热点路径轨迹，易将不同起讫点的路径归为同一类热点路径。

本文优化基于轨迹数据的路径识别方法，以区域网格化为基础，将车辆轨迹压缩为仅关注移动特征的网格序列，序列间的相似性度量包含边界与内部2部分，考虑GPS定位漂移及出行产生与吸引的集聚性，边界网格的相似性通过基于热点网格密度的空间聚类（hot grid density based spatial clustering of application with noise， HG-DBSCAN）得到热点小区度量，内部网格以基于网格的改进LCS相似度表征，二者融合后转化为距离度量，最后进行基于方格序列密度的空间聚类（grid sequence density-based spatial clustering of applications with noise，GS-DBSCAN），优化识别热点路径。

1 热点路径识别优化

1.1 区域网格化

假设研究区域的经度范围为[ψmin，ψmax]，纬度范围为[γmin，γmax]，正方形网格边长为k，将研究区域划分为若干正方形网格。综合考虑路网密度、车辆GPS轨迹点密度及运算效率等因素确定网格尺寸，网格过大，易覆盖同方向相互平行的若干道路；网格过小，会导致大部分网格没有GPS轨迹点落入且运算效率低。

用Gx，y表示网格，x、y分别为Gx，y在网格坐标系下的横、纵坐标。网约车订单i的轨迹点列表为Oi=Pi1，Pi2，…，Pin，…，PiN，其中，N为轨迹点数；Pin（n∈［1，N］）为第n个轨迹点，是包含3项基本信息的一维向量，Pin=（tinψinγin），ψin、γin分别为tin时刻车辆的经、纬度坐标。以Pin为例说明车辆GPS轨迹点与网格的映射关系，公式为：

x=ψin－ψmin/k」y=γin－γmin/k」，（1）

式中 」为取整符号。

1.2 序列边界

GPS定位有随机漂移特征，挖掘热点出行区域时不直接基于轨迹点进行聚类，而是先将轨迹抽象为热点网格，再通过HG-DBSCAN算法聚类，提升搜索效率，且可处理任意形状和大小的簇。采用HG-DBSCAN对热点网格进行空间聚类时，作以下3个基本定义。

定义1 热点网格。Gx，y包含的GPS轨迹起讫点数w应大于预先设定的判断阈值λ。

定义2 网格经、纬度坐标。考虑到Gx，y中GPS轨迹点分布不均匀，采用网格内轨迹点的平均经、纬度表示网格经、纬度坐标，公式为：

ψ—x，y=∑wq=1ψq/wγ—x，y=∑wq=1γq/w。

定义3 网格球面距离。任意2个网格Gx，y、Gx′，y′在经、纬度坐标下的球面距离[23]

d（Gx，y，Gx′，y′）=ΔηR，

式中：Δη为Gx，y的平均经、纬度坐标（ψ—x，y，γ—x，y）、Gx′，y′的平均经、纬度坐标（ψ—′x′，y′，γ—′x′，y′）连线与地球中心线的夹角，Δη=2arcsin（sin2（Δψ/2）+cos ψ—cos ψ—′sin2（Δγ/2）），其中Δψ为2个网格经度之差，Δγ为2个网格纬度之差；R为地球半径。

HG-DBSCAN的网格密度是以热点网格的经纬度坐标为圆心，在指定半径Eps内的热点网格数。若网格密度大于给定的最小核心网格判别数Num，则该网格为核心网格。边界网格指落在某核心网格的邻域内，但本身不是核心网格；噪声网格是既非核心也非边界的网格。HG-DBSCAN算法流程包括输入、初始化、运行、输出。

1）输入。输入λ、Eps、Num。

2）初始化。将分析时间内所有订单轨迹的起讫点映射至对应网格；依据定义1确定热点网格集合H={Gh1，Gh2，…，Ghb，…，GhB}，其中，B为热点网格数，Ghb为第b个热点网格，Ghb=（xyψ—γ—l）hb，其中l为网格的类标签，l=－2，簇编号C=－1。

3）运行。（1）随机选取1个类标签l=－2的热点网格Ghb，若Ghb的Eps邻域内至少有Num个热点网格Gh，则C+1，并将第b个热点网格的类标签lhb赋值为C，令H′为Ghb邻域中的热点网格集合，循环遍历H′中的每个热点网格直至结束，若类标签lhb′＝－2，则将lhb′赋值为C，同时若Ghb′邻域内至少有Num个Gh，则将Ghb′邻域中的热点网格追加至H′；（2）若Ghb的Eps邻域内没有大于或等于Num个热点网格Gh，lhb＝－1；（3）重复步骤（1）（2），直到没有l=－2的Ghb。

4）输出。依据簇内轨迹点数确定热点小区集合Z={Zh1，Zh2，…，Zha，…，ZhA}，其中，A为热点小区数，Zha为第a个热点小区，含若干类标签相同且大于－1的Ghb。

1.3 序列内部

将轨迹点的LCS扩展至网格序列可提升搜索效率，且LCS允许序列部分形变（车辆运动的随机性）。订单轨迹Oi通过式（1）映射为网格序列Si，删除Si中的重复网格，得到压缩后的Si′。考虑网格化下，同一路径的不同轨迹-网格序列受驾驶行为、GPS定位漂移及网格大小等因素影响，网格的重叠率可能较低，建立基于网格的LCS，需定义网格间的空间相似度。

给定2个网格序列Si′={Gi′1，Gi′2，…，Gi′N′}与Sj′={Gj′1，Gj′2，…，Gj′M′}，计算Si′中的第n个网格Gi′n=（t x y）i′n和Sj′中的第m个网格Gj′m=（t x y）j′m间的欧式距离

dG（Gi′n，Gj′m）=（xi′n－xj′m）2+（yi′n－yj′m）2，

式中：xi′n、yi′n分别为Gi′n的横、纵坐标，xj′m、yj′n分别为Gj′m的横、纵坐标。

对网格相似度sG（Gi′n，Gj′m）进行归一化处理，公式为：

sG（Gi′n，Gj′m）=0，dG（Gi′n，Gj′m）>δ1－dG（Gi′n，Gj′m）/δ，dG（Gi′n，Gj′m）≤δ，

式中δ为网格间允许的最大临近距离。

基于网格相似度，通过动态规划方法确定Si′与Sj′间的最长公共序列，需将待求解的问题划分为若干阶段，定义各阶段的状态及变量，确定阶段间的状态转移方程。Si（n）′为Si′前n个网格，Sj（m）′为Sj′前m个网格，将sLCS（Si（n）′，Sj（m）′）状态定义为Si（n）′与Sj（m）′间匹配网格相似度总和的最大值。当n=0或m=0时，sLCS（Si（n）′，Sj（m）′）=0；若n、m均不为0，满足无后效性前提下，sLCS（Si（n）′，Sj（m）′）与Si′前n-1个网格与Sj′前m-1个网格的相似度sLCS（Si（n-1）′，Sj（m-1）′）、Si′前n-1个网格与Sj′前m个网格的相似度sLCS（Si（n-1）′，Sj（m）′）、Si′前n个网格与Sj′前m-1个网格的相似度sLCS（Si（n）′，Sj（m-1）′）有关，分别对应M1、M2及M3 3种匹配模式，M1=sLCS（Si（n－1）′，Sj（m－1）′）+sG（Gi′n，Gj′m），M2=sLCS（Si（n－1）′，Sj（m）′），M3=sLCS（Si（n）′，Sj（m－1）′），即：

sLCS（Si（n）′，Sj（m）′）=0，m=0或n=0

maxM1，M2，M3，m、n≠0。

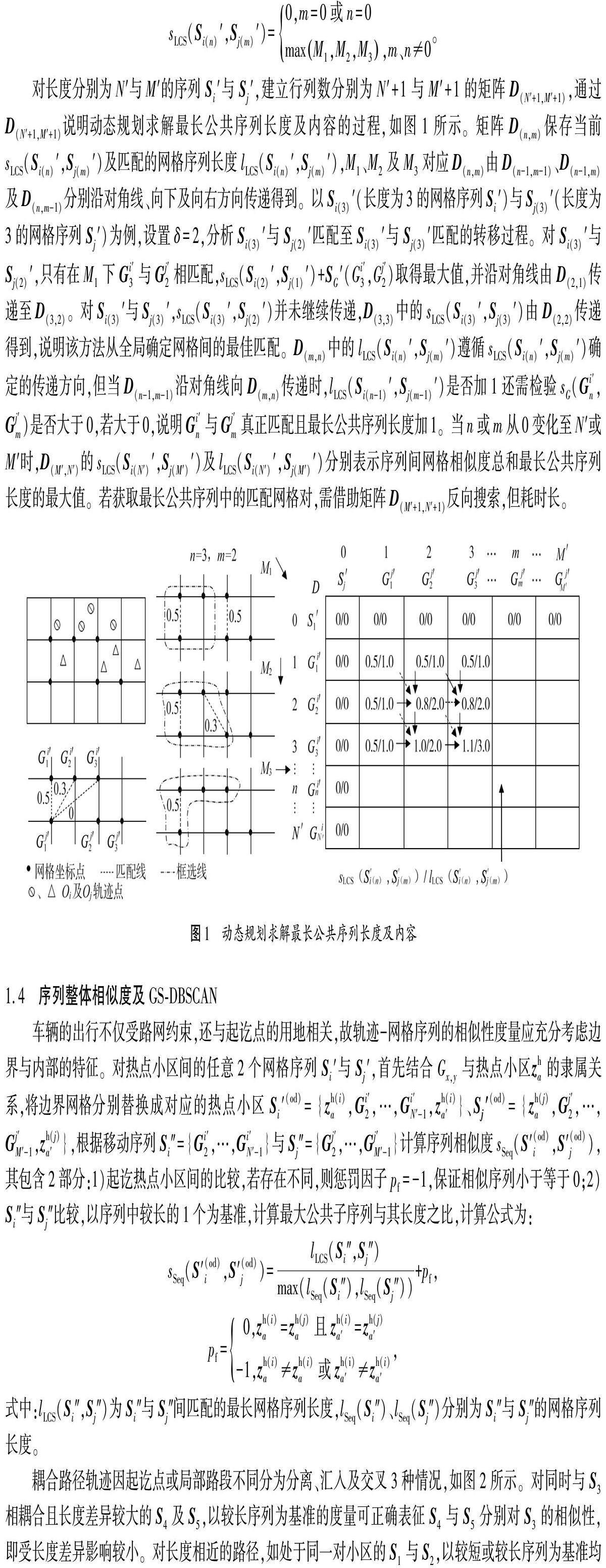
对长度分别为N′与M′的序列Si′与Sj′，建立行列数分别为N′+1与M′+1的矩阵D（N′+1，M′+1），通过D（N′+1，M′+1）说明动态规划求解最长公共序列长度及内容的过程，如图1所示。矩阵D（n，m）保存当前sLCS（Si（n）′，Sj（m）′）及匹配的网格序列长度lLCS（Si（n）′，Sj（m）′），M1、M2及M3对应D（n，m）由D（n-1，m-1）、D（n-1，m）及D（n，m-1）分别沿对角线、向下及向右方向传递得到。以Si（3）′（长度为3的网格序列Si′）与Sj（3）′（长度为3的网格序列Sj′）为例，设置δ=2，分析Si（3）′与Sj（2）′匹配至Si（3）′与Sj（3）′匹配的转移过程。对Si（3）′与Sj（2）′，只有在M1下Gi′3与Gj′2相匹配，sLCS（Si（2）′，Sj（1）′）+SG′（Gi′3，Gj′2）取得最大值，并沿对角线由D（2，1）传递至D（3，2）。对Si（3）′与Sj（3）′，sLCS（Si（3）′，Sj（2）′）并未继续传递，D（3，3）中的sLCS（Si（3）′，Sj（3）′）由D（2，2）传递得到，说明该方法从全局确定网格间的最佳匹配。D（m，n）中的lLCS（Si（n）′，Sj（m）′）遵循sLCS（Si（n）′，Sj（m）′）确定的传递方向，但当D（n-1，m-1）沿对角线向D（m，n）传递时，lLCS（Si（n-1）′，Sj（m-1）′）是否加1还需检验sG（Gi′n，Gj′m）是否大于0，若大于0，说明Gi′n与Gj′m真正匹配且最长公共序列长度加1。当n或m从0变化至N′或M′时，D（M′，N′）的sLCS（Si（N′）′，Sj（M′）′）及lLCS（Si（N′）′，Sj（M′）′）分别表示序列间网格相似度总和最长公共序列长度的最大值。若获取最长公共序列中的匹配网格对，需借助矩阵D（M′+1，N′+1）反向搜索，但耗时长。

1.4 序列整体相似度及GS-DBSCAN

车辆的出行不仅受路网约束，还与起讫点的用地相关，故轨迹-网格序列的相似性度量应充分考虑边界与内部的特征。对热点小区间的任意2个网格序列Si′与Sj′，首先结合Gx，y与热点小区zha的隶属关系，将边界网格分别替换成对应的热点小区Si′（od）={zh（i）a，Gi′2，…，Gi′N′－1，zh（i）a′}、Sj′（od）={zh（j）a，Gj′2，…，Gj′M′－1，zh（j）a′}，根据移动序列Si″={Gi′2，…，Gi′N′－1}与Sj″={Gj′2，…，Gj′M′－1}计算序列相似度sSeq（S′（od）i，

S′（od）j），其包含2部分：1）起讫热点小区间的比较，若存在不同，则惩罚因子pf=－1，保证相似序列小于等于0；2）Si″与Sj″比较，以序列中较长的1个为基准，计算最大公共子序列与其长度之比，计算公式为：

sSeq（S′（od）i，S′（od）j）=lLCS（Si″，Sj″）max（lSeq（Si″），lSeq（Sj″））+pf，

pf=0，zh（i）a=zh（j）a且zh（i）a′=zh（j）a′－1，zh（i）a≠zh（i）a或zh（i）a′≠zh（i）a′，

式中：lLCS（Si″，Sj″）为Si″与Sj″间匹配的最长网格序列长度，lSeq（Si″）、lSeq（Sj″）分别为Si″与Sj″的网格序列长度。

耦合路径轨迹因起讫点或局部路段不同分为分离、汇入及交叉3种情况，如图2所示。对同时与S3相耦合且长度差异较大的S4及S5，以较长序列为基准的度量可正确表征S4与S5分别对S3的相似性，即受长度差异影响较小。对长度相近的路径，如处于同一对小区的S1与S2，以较短或较长序列为基准均可，前者比后者更接近1；但对不同小区的S3与S6，2种度量方法均存在局限性，此时需增加起讫边界小区不同的限制条件进行区分。

计算Si′（od）与Sj′（od）间的相似度后，需转化为距离度量才可进行GS-DBSCAN聚类，公式为：

dSeq（Si′（od），Sj′（od））=1－sSeq（Si′（od），Sj′（od））。

GS-DBSCAN的伪代码与HG-DBSCAN类似，研究对象变成网格序列，不再赘述，得到热点路径集合R={rh1，rh2，…，rhU}，其中U为热点路径数。

2 案例分析

以2017-01-13青岛市市南区的网约车订单数据为案例验证方法的有效性。区域覆盖的经度区间为（120.375 6°，120.400 0°），纬度区间为（36.063 1°，36.075 9°），面积约为4.79 km2。案例共采集33 538条订单轨迹数据，每条订单数据包含脱敏处理后的订单编号及轨迹点列表2个字段，如订单编号3e7a3f2d231的轨迹点列表为{（1 484 236 791 s 120.398 56° 36.007 014°），（1 484 236 794 s 120.398 57° 36.070 17°），（1 484 236 977 s 120.398 55° 36.070 18°）}，轨迹点列表中包含Unix时间戳及WGS84坐标系下的经、纬度。

2.1 热点路径识别结果

先聚类识别热点小区，再将热点小区作为网格边界，增加约束条件，聚类识别热点路径。取网格尺寸为30 m×30 m，小于次干路及以上等级道路间的最小平行距离。假设车辆

在网格内的位置均匀分布且速度为36～55 km/h，轨迹点平均采样时间为3 s，则车辆每次移动的网格数为1.0～1.5。

首先建立参数不同间隔取值下的交叉组合，通过试算，设置λ=30，Eps=30 m，Num=2。根据所选组合进行HG-DBSCAN聚类，聚类后的簇总数为82，根据簇中包含的出行起讫点数降序排列选取前13个簇作为热点小区，如图3所示。

由图3可知：该区域内的热点小区多分布在研究范围内道路的端点处，表示联系研究范围外热点区域的主要途经点。zh12和zh13位于研究范围内道路中间，结合该点的用地可知，周边商业综合体华润万象城成为农历新年前最后1个工作日的出行热点。从热点小区间出行期望线可知zh12与zh1间的联系最强，说明华润万象城是研究范围内有强吸引力的出行热点，同时对研究范围外从zh1方向的居民有较强吸引力。

选取早、晚高峰时段（07：00—10：00，18：00—21：00）数据识别热点路径。通过试算，设置δ=2，Eps=0.2 m，Num=3。对13个热点小区间的轨迹-网格序列进行GS-DBSCAN聚类，选取其中序列数较多的前20个簇作为热点路径集合，如图4所示。由图4结合热点小区分布可知：热点路径主要分布在主干道，受相交道路或道路一侧邻近热点小区的吸引，又存在若干条转入、转出的高相似路径。

2.2 基于LCS的序列相似性度量算法对比与网格敏感性分析

保持δ=2，Eps=0.2 m，Num=3不变，对比分析不同计算方法下的聚类效果。方法1：只考虑内部相似性且以对比序列中较短序列为基准。方法2：只考虑内部相似性且以对比序列中较长序列为基准。方法3：本文建立同时考虑边界与内部相似性的GS-DBSCAN聚类且以对比序列中较长序列为基准。

以zh1至zh5、zh7、zh9的网格序列集为例分别进行3种方法下的轨迹聚类，得到的簇如图5所示。由图5可知：方法3中的5个轨迹簇C0、C1、C2、C3、C4对应区域中的路径rh2、rh7、rh14、rh21、rh22；方法1中以较短序列为基准，C1与其他簇轨迹的相似度均较高，在密度可达的传递作用下将其归于1类；方法2中虽以较长序列为基准，但C0与C2序列长度相近且重叠度较高，导致rh2与rh14无法区分；方法3中C0、C1、C2、C3、C4可较好地区分rh2、rh7、rh14、rh21与rh22的轨迹，说明本文考虑边界与内部相似性，且以对比序列中较长序列为基准的方法合理。

分析GS-DBSCAND方法对网格尺寸的敏感性，在k=30 m的基础上分别缩小、扩大1倍，相应地调整δ进行聚类，得到不同路径下的正确轨迹数，如表1所示。

由表1可知：聚类时间随k的减小而增大，当δ=4，k=15 m时，聚类时间约为440 s，仅比δ=2，k=30 m时的聚类时间增大43.32%，GS-DBSCAN方法的轨迹聚类运算效率较高；不同k和δ下，rh2、rh7、rh14、rh21及rh22的聚类结果整体偏差小于2%，受k和δ的影响较小。

3 结束语

为准确识别热点路径，本文提出细分边界与内部两部分度量序列间相似性的轨迹数据热点路径识别优化方法，以区域网格化为基础，将车辆轨迹映射为移动网格序列，通过HG-DBSCAN算法识别热点区域，再将热点区域作为网格边界，增加约束条件，通过GS-DBSCAN算法识别热点路径。以青岛市市南区的网约车订单数据为案例进行热点路径识别，验证方法的有效性。结果表明：本文提出的移动网格序列研究方法能准确识别热点小区，正确区分多出行起讫点分布下长度差异较大的分离、汇合与交叉耦合热点路径，且聚类运算效率较高，可为城市范围内交通组织设计、交通拥堵治理、智慧交通出行路径规划等城市交通规划设计与管理提供参考依据。后续将结合实际工作，采集私家车、共享单车等更丰富的轨迹数据，扩大案例范围，开展更全面的研究。

参考文献：

[1] WANG Y L， QIN K， CHEN Y X， et al. Detecting anomalous trajectories and behavior patterns using hierarchical clustering from taxi GPS data[J].ISPRS International Journal of Geo-Information， 2018，7（1）：25-45.

[2] ZHANG D Q， LI N， ZHOU Z H， et al. Ibat： detectiong anomalous taxi trajectories from GPS traces[C]//Proceedings of 13th International Conference on Ubiquitous Computing. Beijing， China： Ubicomp，2011：17-21.

[3] LIU C K， QIN K， KANG C G. Exploring time-dependent traffic congestion patterns from taxi trajectory data[C]//2015 2nd IEEE International Conference on Spatial Data Mining and Geographical Knowledge Services （ICSDM）. Fuzhou， China：IEEE，2015：39-45.

[4] 陈振华.基于轨迹数据的城市交通拥塞传播模式挖掘[D].吉林：吉林大学，2019.

[5] LIN S， SCHUTTER B D， XI Y G， et al. Efficient network-wide model-based predictive contral for urban traffic networks[J].Transportation Research Part C： Emerging Technologies， 2012，24：122-140.

[6] MAZIMPAKA J D， TIMPF S. Trajectory data mining： a review of methods and applications[J].Journal of Spatial Information Science，2016，13：61-99.

[7] 李颖，赵莉，赵祥模，等.基于大货车GPS数据的轨迹相似性度量有效性研究[J].中国公路学报，2020，33（2）：146-157.

[8] KIM J， MAHMASSANI H S. Spatial and temporal characterization of travel patterns in a traffic network using vehicle trajectories[J].Transportation Research Part C： Emerging Technologies， 2015，7（10）：164-184.

[9] 冯琦森.基于出租车轨迹的居民出行热点路径和区域挖掘[D].重庆：重庆大学，2016.

[10] 赵欣.基于时空约束的城市热点区域与热点路径挖掘[D].重庆：重庆大学，2017.

[11] KANG H Y， KIM J S， LI K J. Similarity measures for trajectory of moving objects in cellular space[C]//Proceedings of the 2009 ACM Symposium on Applied Computing. Honolulu， Hawaii， USA： Spatial Information Society，2009：9-12.

[12] 吴俊伟，朱云龙，库涛，等.基于网格聚类的热点路径探测[J].吉林大学学报（工学版），2015，45（1）：274-282.

[13] 王超.基于轨迹聚类的频繁模式挖掘方法[D].杭州：浙江大学，2021.

[14] LEE J G， HAN J W， WHANG K Y. Trajectory clustering： a partition-and-group framework[C]//Proceedings of the 2007 ACM SIGMOD International Conference on Management of Data. Beijing， China： SIGMOD，2007：593-604.

[15] KANG H Y， KIM J S， LI K J. Similarity measures for trajectory of moving objects in cellular space[C]//Proceedings of the 2009 ACM Symposium on Applied Computing. Honolulu， Hawaii， USA：ACM Symposium on Applied Computing， 2009：1325-1330.

[16] YANG H， SASAKI T， IIDA Y， et al. Estimation of origin-destination matrices from link traffic counts on congested networks[J].Transportation Research Part B： Methodological， 1992，26（6）：417-434.

[17] ZHOU X S ， MAHMASSANI H S. Dynamic origin-destination demand estimation using automatic vehicle identification data[J].IEEE Transactions on Intelligent Transportation Systems， 2006，7（1）：105-114.

[18] OU J S， LU J W， XIA J X， et al. Learn， assign， and search： real-time estimation of dynamic origin-destination flows using machine learning algorithms[J].IEEE Access， 2019， 7：26967-26983.

[19] TANG K S， CAO Y M， CHEN C， et al. Dynamic origin-destination flow estimation using automatic vehicle identification data： a 3D convolutional neural network approach[J].Computer-Aided Civil and Infrastructure Engineering， 2021，36（1）：30-46.

[20] CAO P， MIWA T， YAMAMOTO T， et al. Bilevel generalized least squares estimation of dynamic origin-destination matrix for urban network with probe vehicle data[J].Transportation Research Record： Journal of the Transportation Research Board， 2013， 2333：66-73.

[21] CAO P， MIWA T， YAMAMOTO T， et al. Estimation of dynamic link flows and origin-destination matrices from lower polling frequency probe vehicle data[J].Journal of the Eastern Asia Society for Transportation Studies， 2013，10：762-775.

[22] HUANG T， MA Y T， QIN Z T， et al. Origin-destination flow prediction with vehicle trajectory data and semi-supervised recurrent neural network[C]//2019 IEEE International Conference on Big Data. Los Angeles， CA， USA：IEEE， 2019：1450-1459.

[23] GODAU M， ALT H. Computing the Fréchet distance between two polygonal curves[J].International Journal of Computational Geometry & Applications， 1995，5（1）：75-91.

Regional hotspot path identification based on grid clustering optimization

WENG Xuyan， ZHENG Shuni

Zhejiang Scientific Research Institute of Transport， Hangzhou 310023，China

Abstract：To solve the problem that the trajectory clustering method is difficult to accurately identify high-similarity hotspot paths， a hotspot path identification method that can distinguish between start and end points or local sections is proposed. The travel trajectory is mapped and compressed into a moving mesh sequence， and the spatial similarity measurement between sequences is distinguished from the boundary and the interior， integrated and transformed into distance， and spatial clustering based on grid sequencedensity-based spatial clustering of applications with noise （GS-DBSCAN） is performed. Taking the trajectory data of some taxis in Shinan District， Qingdao as an example， the clustering method that only considers internal similarity and is based on the shorter and longer sequences in the comparison sequence is verified. The results show that the GS-DBSCAN algorithm， which considers both boundary and internal similarity and is based on longer sequences， can correctly distinguish the separation， convergence， and cross-coupling hotspot paths with large length differences under the distribution of multiple travel start and end points. The influence of variable differences such as path length and grid size is less than 2%， and the clustering operation efficiency is high.

Keywords：hotspot path; boundary; interior; trajectory clustering

（责任编辑：赵玉真）

收稿日期：2023-02-02

基金项目：浙江省交通运输科技计划项目（2023001）

第一作者简介：翁旭艳（1993—），女，上海人，工程师，工学硕士，主要研究方向为城市交通，E-mail：2445951226@qq.com。

DOI：10.3969/j.issn.1672-0032.2024.02.013