聚焦单元复习　关注生活数学

2024-06-18吴敏

小学教学参考(综合) 2024年5期

吴敏

［摘要］以苏教版数学教材五年级下册“圆”的单元复习课为例，开展一系列的教学活动：通过单元梳理，帮助学生整理单元知识；通过提出问题，帮助学生深入理解单元知识；通过解决问题，帮助学生巩固与掌握单元知识。这样聚焦单元复习课，关注生活中的数学，能让学生更好地掌握所学的单元知识，提升他们的数学素养和综合能力。

［关键词］苏教版；数学教材；单元复习课

［中图分类号］ G623.5［文献标识码］ A［文章编号］ 1007-9068（2024）15-0019-03

《义务教育数学课程标准（2022年版）》强调：“学生通过数学课程的学习，掌握适应现代生活及进一步学习必备的基础知识和基本技能、基本思想和基本活动经验。”因此，学生不仅要从数学课本中学习知识，更要学会用数学知识解决生活中的实际问题。这样不仅可以帮助学生解决日常生活中的各种实际问题，如购物时的价钱计算等，还能让学生学会如何发现与分析问题，找到解决问题的方法，从而提高自身解决问题的能力。

如教学苏教版数学教材五年级下册“圆”的单元复习课时，教师先引导学生回顾和整理本单元的核心知识，帮助学生巩固圆的基本概念，形成系统的知识框架；再出示一系列与生活实际紧密相关的问题，让学生运用所学的圆的知识去解决问题，体会数学在实际生活中的应用价值。

【教学实践】

一、单元梳理，整理单元知识

单元整理和复习在学生的学习过程中起着非常重要的作用。通过整理和复习，学生可以系统地回顾和巩固本单元所学的知识，加深对所学知识的理解。同时，这样有助于培养学生的知识整理能力、自主学习能力，构建完整的知识体系。

师：同学们，这节课我们来复习“圆”这个单元的知识。课前，大家制作了思维导图和手抄报，现在一起来欣赏同学们的作品。老师觉得大家整理的内容和形式虽然各不相同，但是都整理了这个单元中重要的知识点。那么，这个单元有哪些重要的知识点呢？

生1：这个单元，我们学习了“圆的认识”“圆的周长”“圆的面积”“组合图形的面积”等内容。

师：我们认识了一种新的图形——圆，而扇形和圆环是对圆的知识的拓展。你能具体说说学习了哪些知识点吗？

生2：在“圆的认识”里，我知道在同一个圆中，所有的半径、所有的直径都相等，且直径长度是半径的2倍；在“圆的周长”里，我知道圆的周长公式是C=2πr=πd；在“圆的面积”里，我知道圆的面积公式是S=πr2；在“扇形的认识”里，我知道扇形是圆的一部分，两点之间的曲线是弧，顶点在圆心的角叫作圆心角……

上述教学片段，教师借助学生整理的作品开展复习课教学，这样既能快速揭示这节课的学习内容，帮助学生回忆本单元学过的知识，又可以深化学生对所学知识的理解，增强复习教学的效果。

二、提出问题，深化知识理解

著名科学家爱因斯坦说过：“提出一个问题比解决一个问题更重要。”当学生面对有趣或具有挑战性的问题时，他们会被吸引并愿意投入时间和精力去思考与解决问题。通过解决问题，学生可以更加深入地理解数学概念和思想方法，巩固和拓展所学的数学知识。

师：在知识整理的过程中，同学们还收集了生活中有关圆的问题。（出示问题：一枚1元硬币的直径应该怎么测量？）有同学提出了这个问题。你想用什么办法来测量1元硬币的直径长度？

生1：可以先把1元硬币放在白纸上，沿着硬币的外边缘用铅笔画下来；然后把纸上的硬币用剪刀剪下来，并将这个圆形对折一次；最后用尺子测量出这条折痕的长度，就是1元硬币的直径了。

生2：先用绳子绕1元硬币的外边缘一圈，就是这个圆的周长，再利用圆的周长公式计算出1元硬币的半径，最后乘以2就是1元硬币的直径了。

生3：我觉得可以用一把尺子在硬币上上下移动，最长的长度就是1元硬币的直径。

师：同学们用不同的方法解决了关于圆的直径的测量问题。（出示问题：比萨店老板说一个12寸比萨和两个6寸比萨的价格一样。你觉得买哪种比萨更划算？）你会选择买一个12寸比萨，还是买两个6寸比萨呢？其实，这个问题是在比较比萨的周长还是面积？（面积）那我们就来算一算一个12寸比萨和两个6寸比萨的面积分别是多少。

生4：一个12寸比萨的半径是6，所以面积是3.14×62=113.04；一个6寸比萨的半径是3，所以两个6寸比萨的面积是3.14×32×2=56.52。通过计算发现，一个12寸比萨的面积大，所以我们买一个12寸比萨更划算。

生5：我觉得只要用π的字母式表示就可以了，即一个12寸比萨的面积是36π，两个6寸比萨的面积是18π，所以我们买一个12寸比萨更划算。

生6：也可以画图来比较，由于两个6寸比萨在里面，一个12寸比萨在外面，所以我们买一个12寸比萨更划算。

……

上述教学片段，为了更好地帮助学生将抽象的数学知识与实际生活联系起来，教师鼓励他们积极提出与圆的周长和面积有关的生活问题，并让他们运用圆的周长和面积公式来解决这些问题。这样不仅能够激发学生思考和探索的兴趣，培养学生的思维能力，还能够深化学生对数学概念和方法的理解，提高学生解决实际问题的能力。

三、解决问题，巩固所学知识

解决问题是数学教学的核心目标之一，要求学生能够运用所学的数学知识来解决现实生活中的具体问题。当学生开始运用所学的数学知识来解决生活中的实际问题时，他们会发现数学学习不再枯燥无味，而是变得生动有趣。

1.研究圆与圆的关系

师：学习“圆”这个单元后，同学们对圆特别感兴趣。（出示泡泡的图片）这是美丽的泡泡，它是一个立体图形。现在发挥你们的想象，如何让它变成圆呢？

生1：给泡泡拍照，在平面上就是圆了。

师：看，这里有一种特殊的圆（出示图1），大圆在外，小圆在内。请你仔细观察这两个圆，说说它们之间有什么关系。可以从两个圆的半径、直径、周长和面积等方面来思考。

生2：假如把小圆的半径看作1，那么大圆的半径就是2，所以大圆半径是小圆半径的2倍；假如小圆的直径是2，那么大圆的直径就是4，所以大圆直径是小圆直径的2倍；假如小圆的周长是2π，那么大圆的周长就是4π，所以大圆周长是小圆周长的2倍；假如小圆的面积是π，那么大圆的面积就是4π，所以大圆面积是小圆面积的4倍。

师：这位同学用假设法推导出两个圆的半径、直径、周长和面积的倍数关系。如果大圆的半径是小圆半径的3倍，那大圆与小圆之间的直径、周长和面积有怎样的关系呢？

生3：我们可以把小圆的半径看作1，那么大圆的半径就是3，这样小圆的直径是2，大圆的直径是6，所以大圆直径是小圆直径的3倍；把小圆的周长看作2π，那么大圆的周长就是6π，所以大圆周长是小圆周长的3倍；把小圆的面积看作π，那么大圆的面积就是9π，所以大圆面积是小圆面积的9倍。

师：如果大圆的半径是小圆半径的n倍，大圆与小圆之间的直径、周长和面积又有怎样的关系呢？

生4：大圆直径是小圆直径的n倍，大圆的周长是小圆周长的n倍，大圆面积是小圆面积的n2倍。

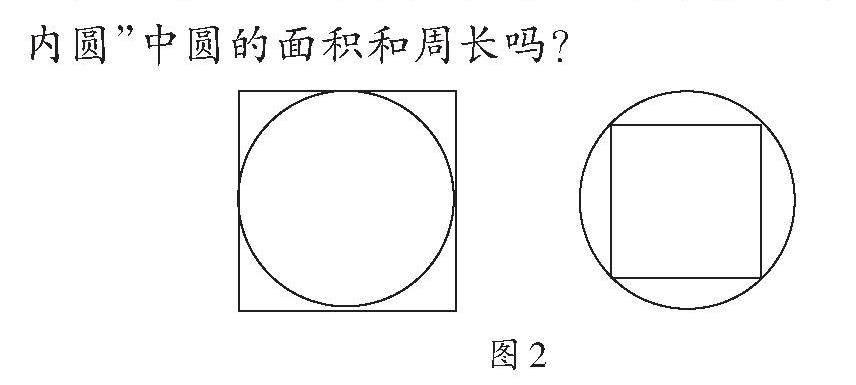
2.研究“外方内圆”的情况

师：刚才我们解决了圆与圆之间的问题。（出示图2）中国建筑中经常能见到“外方内圆”和“外圆内方”的设计。我们先来研究“外方内圆”这种情况。如果把圆的半径看作1米，你能计算出“外方内圆”中圆的面积和周长吗？

图2

生5：如果把圆的半径看作1米，那么圆的面积S=πr2=π（平方米），周长C=2πr=2π（米）。

师：那正方形的面积和周长是多少呢？

生6：如果把圆的半径看作1米，那么正方形的边长是2米，正方形的面积S=a×a=2×2=4（平方米），正方形的周长C=4a=4×2=8（米）。

师：那你能计算正方形和圆之间部分的面积吗？

生7：我们已经知道正方形的面积是4平方米，圆的面积是π平方米，所以正方形和圆之间部分的面积=4-π=4-3.14=0.86（平方米）。

3.研究“外圆内方”的情况

出示题目：如果把圆的半径看作1米。（1）计算“外圆内方”中圆的面积和周长。（2）计算正方形的面积。（3）计算正方形和圆之间部分的面积。

师：同学们，我们研究了“外方内圆”的情况，现在请你自己完成学习单中“外圆内方”的练习。

生8：如果把圆的半径看作1米，那么圆的面积S=πr2=π（平方米），周长C=2πr=2π（米）。正方形可以看成两个三角形组成，其中三角形的底就是圆的直径2，三角形的高是圆的半径1，所以正方形的面积S=（2×1÷2）×2=2（平方米），正方形和圆之间部分的面积=π-2=3.14-2=1.14（平方米）。

生9：对正方形的面积，我还有不同的计算方法。如果把正方形的边长看作a，正方形的对角线正好是圆的直径2，所以2a2=2×2=4，a2=2，即正方形的面积是2。

4.解决生活实际问题

师：接下来，我们用圆的知识来解决生活问题。

出示题目（1）：学校要修建一个半径2米的圆形花坛（见图3），黑色的部分种海棠花，其余部分铺草坪，已知海棠花的面积是3.14平方米，请问需要铺草坪多少平方米？

生10：我们知道大圆的半径是2米，所以大圆的面积S=πr2=3.14×22=12.56（平方米）；海棠花的面积是3.14平方米，所以铺草坪的面积=12.56-3.14=9.42（平方米）。

生11：由于大圆面积是小圆面积的4倍，且已经知道小圆面积是3.14平方米，所以铺草坪的面积=3.14×（4-1）=9.42（平方米）。

出示题目（2）：体育老师在操场上画了两个大小不等的圆（见图4），准备组织同学们做游戏。测量后得知，甲圆的直径是乙圆直径的2/3，乙圆的面积是3.6平方米，甲圆的面积是多少平方米？

生12：我们已经知道甲圆的直径是乙圆直径的2/3，所以甲圆的面积是乙圆面积的2/3的平方；又因乙圆的面积是3.6平方米，所以甲圆的面积是3.6×2/3×2/3=1.6（平方米）。

……

上述教学片段，教师围绕研究圆与圆的关系、解决生活实际问题等四个方面，丰富学生对圆的认识和应用，让他们深刻体会到了数学在实际生活中的应用价值。这会让学生更加珍惜学习数学的机会，更加自信地面对未来的学习和挑战。

【教学反思】

通过复习课教学，学生对圆的知识有了更深刻的理解，并广泛地运用所学的数学知识解决一些生活实际问题。