基于复合梯度算法的在线教育评价系统研究
2024-06-14陶槊魏东东陈滨王强志
陶槊 魏东东 陈滨 王强志

收稿日期:2022-05-20
基金项目:安徽省教育厅继续教育教学改革项目(2021jxjy054);安徽省高校教学实训基地项目(2021jyxm1532)
作者简介:陶槊(1974—),男,硕士,副教授,从事信息安全与数据挖掘研究.Email:1287982006@qq.com
通信作者:魏东东(1990—),男,讲师,从事云计算与电子商务研究.Email:604487312@qq.com
摘要:依托在线教育的大数据技术,建立一套改进的在线教育评价指标体系.根据该系统特点,利用智慧校园信息系统后台,获取主客观评价数据并加以整合与处理.通过基于改进的复合梯度算法计算最优权重,处理评分数据,以获得能反映实际教学水平的综合成绩.实验结果表明,该算法是有效的.
关键词:在线教育;梯度算法;大数据;复合权值
中图分类号:G434
文献标志码:A
0引言
在线教育评价是一项综合性工程,需要对教育性质与能力的总体说明,也需要质量体系的内容界定与指标衡量.因此,对在线教育的研究必须先建立一套科学的教育评价系统与标准规范,明晰考评指标,然后通过有效方法提升考评效果.
目前,在此方面主流的评价模式[1-2]有欧盟远程教育大学联合会(European association for distance teaching universities,EADTU)颁布的卓越标准(Excellence)和美国在线学习联盟推出的网络教学实践评价指标体系(quality course teaching and instructional practice scorecards,QCTIP)[3]等.我国还没有体系化的远程教育评价系统应用实例,对评价系统的研究也主要局限于分类统计、特征分析、模式匹配及神经网络等领域[4].本研究着重将在线教育特征指标化,并采集整理支持指标的信息数据,转换成对应的初始评价数据,然后探讨复合算法,对评价数据进行综合运算,求得综合评价结果,并根据作者所在高校5年来的在线教育成果进行对比,验证了采集数据与算法的正确性与功效性.
1在线课堂评价系统的建立
1.1评价指标的确定
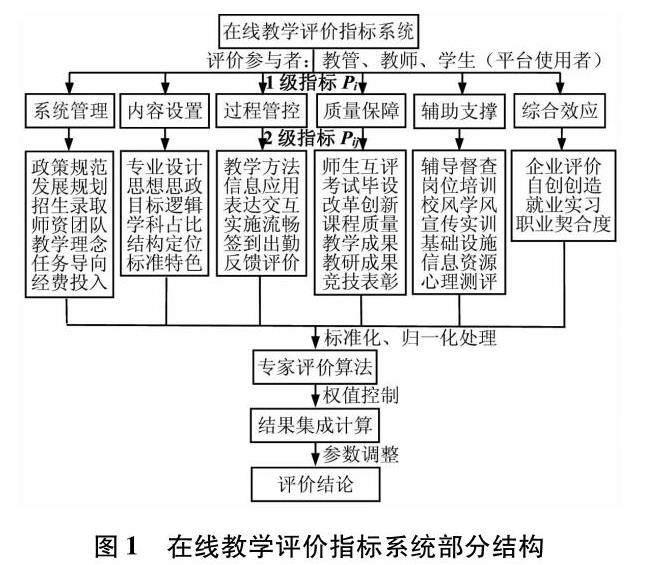
进行课程网络教学评价工作前,必须明晰在线课堂的内容与特征要素,然后根据网络技术特点,按专家知识指导和教育主管部门工作要求,设定在线教育关联考核指标,并需要保证全部指标的概括性与指向性,避免过多元素的组合,影响最后评价成绩的合理性,特别是要防范教学评价的重复性及不一致性.根据这一原则,参照文献[5-6]提出的一系列考核规范,仿照境况/输入/过程/成果模型(context/input/process/product,CIPP)[7],建立本研究的远程“在线教育”3级评价指标系统.在线教学评价指标系统部分结构如图1所示.
1.2评价系统的建立
根据评价系统结构与特点,以专业与教学的实施过程开展该评价系统的建设与研究.该评价系统的具体开发过程如下:1)对条件、专业、课程及成果的各项条目进行分解,与上述建立的3级指标系统相对应,对教育教学活动产生的各类数据进行指标化定义.2)考评要素制定与选取:对远程教学、智慧课堂系统及智慧校园网络信息系统等各平台进行整合,选取教学评价有关的信息,关联对应的数据接口.3)智慧校园网络信息系统与大数据分析算法的选用:评估内容的设计;评价系统的管理数据选择;指标数据的制备、采样、抽取、清洗与转换等;评价内容、流程及模型的建立.4)评价系统平台的设计:大数据平台的多次再整合;不断重复步骤2匹配指标元素;教学效果评估模型与算法的设计;优化评估模型、处理流程与关联数据等.5)测试与验证:计算、验证、调整参数及再计算;如不符合预期,则回到步骤3重新调整算法、权重及数据等,最后总体测试;每步重复多次,直到输出稳定并符合预期.6)可视化界面设计、标准定制与规范化应用及评价效果的完善.
2评价数据的处理
2.1获取途径
传统的专家考核系统与问卷抽样调查存在主观偏差、手段单一且反馈滞后等问题,因此需要通过更广泛的数据来保证评价的准确性与客观性,而直接的权值统计会造成定性评价的缺失,无法有效表达在线课堂的多样性.本研究利用作者所在高校的课堂教学分析系统、平台监测系统及智能点播等系统累计的大数据便利,按照在线教育指标要求,选择采集相关数据,然后清洗整合,转换对应的评分数据.其中,指标所需评价数据的获取形式如表1所示.
从表1可知,通过各个信息平台获得的数据有些可以直接经转换后作为评分代入到指标运算中,而有些则以互评及问卷调查的形式获取相关评分.
由于智慧高校平台分散各处且接口庞杂多样,这就要用到第3方开源平台如spark或hadoop大数据分布管理系统实现对各个指标数据源进行统一收集与管理,再向上传给评价系统预处理软件,进行分值计算.
2.2数据的标准化
设第1级指标系统集P={P1,…,PI},第2级指标系统集Pi={Pi1,…,PiJ},i{1,…,4},j{1,2,…,J},JZ+,则从各平台接口获得初始得分s′ij:
s′ij=1K∑Kk=1wijk∑Xx=1sxijk(1)
式中,wijk为第k项初级评分权重,wij={wij1,...,wijK},且wij=∑Kk=1wijk=1;评分量xX,KZ+,XZ+.对应i级m个指标n个评分有矩阵S=(sij)m×n.
鉴于评价源数据来自各个平台,为了去量纲化,在评分计算前,必须先对sxij进行标准化处理.根据不同评估目的,选择不同的标准化模式,以2到3级评分为例,如果作为高校间评比需要,采用优选指标(见式(2))以体现课程结构合理性与教学能力.若作为教学问题方面的研究,则使用差选指标(见式(3)).
s*′ij=sij-min(si)max(si)-min(si)(2)
s*ij=max(si)-sijmax(si)-min(si)(3)
于是第i项平均值*i=1J∑Jj=1x*ij,标准差σi=1J-1(∑Jj=1(s*ij-*i)2,统一量纲后的评分为:
sij=s*ij-*iσi(4)
Pi内每个指标会有m个评分(m{1,2,…,M},MZ+),于是得到评分矩阵Si:
Si=s1i1s2i1…smi1s1i2s2i2…smi2s1ijs2ij…smij(5)
同时指标权重wij=∑Kk=1wijk,wi=∑Jj=1wij,W=∑6i=1wi=1,ij=1M∑Mm=1smij,则Pi的指标得分为,
si=∑Jj=1ijwij(6)
3赋权算法
各级指标Pi权值的确定是保证远程教学评价准确与客观性的基础.赋权算法[8-9]有多种,典型的有层次评估法与遗传神经网络算法,但各有优劣,前者减少了主观判断的随意性,但精度不高,后者更能反映指标评价系统的实际结果,但计算和训练过程多且操作复杂.本研究以改进动态层次评估法(dynamic analytic hierarchy process,DAHP)和相关性指标权重确定法(criteria importance through intercriteria correlation,CRITIC)为基础,这样既能充分利用智慧高校平台的评价大数据,又兼顾远程教育特有的专业要求,同时弱化各种算法的不足.
3.1改进DAHP算法
针对从各个信息平台取得的课程评价与问卷调查及打分者主观评价存在的心理偏差,本研究采用DAHP算法来解决打分者的主观不确定性.DAHP算法针对粒子群(评价目标)变化时,对粒子进化(多目标的变化)进行度量,因而算法需要自适应更新相关联的指标权重和学习因子,以实时应对评分的不确定性[10].同时,对DAHP进行改进,使用Saaty5标度表求指标间综合性级别,并用敏感因子根据指标层与判断层间的重要关系确定最终得分.设调查评分等级分为5个区间,由低到高分别是差、较差、一般、较好与好,则成绩定义的集合为Y={y1,y2,y3,y4,y5},对应元素y的取值区间为yl=(0~0.2|0.2~0.4|0.4~0.6|0.6~0.8|0.8~1).对相关指标Pi进行比较,成绩区间Pia、Pib∈yl,且a≤b,且a,b{1,2,…,M},l{1,2,…,5},于是2级i指标a,b间关系[11]:
flab=0,重要性Pb
于是M个评分的Pab相互比较时,对应指标序列有关联映射f:F(f)←S,即Si的关联度为F(fi),得到一致性判断矩阵:
Fli=fl11…fl1MflM1…flMM(8)
令alm=∑Mn=1flmn,且m,n{1,2,…,M},得到一致性判断矩阵Ai=(al)M,于是有判断式:
ei=∏Mm=1(∑Mn=1(Aim-Ain)2λM+1)(9)
式中,敏感因子λ=(0,1,2,3).根据综合权值区间决定,组成判断矩阵Eij=(eij)I×J,得权值:
w′i=Iei/∑Ii=1ei(10)
3.2CRITIC赋权算法
教学评价指标的定量成绩具有可比性,但限于教学对象、培养目的、课程结构与辅助条件的影响,也存在着各指标强度不一致与衡量标准冲突等方面的问题,所以需要通过客观赋权法来控制指标间的数量差异性与内容关联性.为应对大数据网络评价动态性,本研究采用的是CRITIC算法,即用指标间的对比强度和不一致性来处理评分大小.设评分样本处理后,消除了随机异常,则Pij指标的相关系数rmijk[12]:
rmijk=(J-1)∑Mm=1(smij-mi)∑Mk=1(smik-mi)(∑Jj=1(s*ij-*i)2)(∑Jj=1(s*ik-*i)2)(11)
Rij=∑Jk=1(1-rijk)(12)
式中,j,k{1,2,…,J},得到指标i的信息量:
Cij=1M∑Mm=1smij∑Jj=1(1-Rij)(13)
于是得到2级指标客观权重:
wij=Cij∑Jj=1Cij(14)
4最优权值组合
4.1复合算法
通过2种或多种算法获得初始权重后,要保证评价的有效性,还需要以最优的wi组合,力求实现评分的客观性和综合性.其中,经典直接的方法是计算wi和各对应初始权值的Euclidean距离,如式(15)所示:
D(wi)=∑Ii=1(wi-w′i)2+∑Ii=1(wi-w"i)2(15)
当存在min(D(wi))≥0时,wi与各初始权值的差异最小,即获得最优wi集.设D(w)连续可微,且D(w)为凸函数,则可以采用交替向乘子算法(alternative direction method of multipliers,ADMM)计算wi值[13].ADMM作为增广拉格朗日算法(augmented Lagrange multiplier algorithm,ALM)的改进,好处在于,增加2次惩罚参数强化约束,将全局最优解转换为局部最优解计算,同时用对偶交替计算的方式,迭代更新实现收敛,因此在求最优解方面获得了广泛应用.
根据ADMM算法求约束条件下最优解wi:
minw1,w2,…,wi,zD(wi)+g(z),x∈RI,z∈RI′s.t.wi=z,i=(1,2,…,I) (16)
式中,z为全局变量,z∈RI.RI为指标系数I取值范围.于是,通过交替迭代的方式求解局部变量wi,在某个收敛区间获得最优解.根据ADMM算法将上式转换为:
Lρ(wi,z,λ)=∑Ii=1D(wi)+g(z)+
ρ2∑Ii=1‖wi-z‖22+∑Ii=1λT(wi-z)(17)
式中,Lρ为Lagrange乘子,λ为对偶变量,ρ为惩罚参数,同时∑Ii=1wi=1.经线性约束项转换,用ALM乘子转换[12]得到式(18):
Lρ (wi ,z,μ) = ∑Ii = 1D(wi ) + g(z) + ρ2∑Ii = 1‖wi -zi + μ‖22(18)
式中,μ为对偶可调量,据此实现局部变量wi的交替更新.
大数据环境下对原算法改进,即采用分项计算wi,获取最优权值.因评价数量m[1,M],MZ+,smi是第i项指标第m个评分,且函数连续可微,则根据Moreau Decomposition[14]梯度下降转化法,且在式(18)的约束下,取λ=1/2,令μ为交替变量,D(wi)=ρ∑Mm=1max1-smiwi,0,g(z)=(1/2)‖z‖22,于是获得迭代过程如下:
wk + 1i = argminwi D(wi ) + ρ2‖wi -zk + μki‖22zk + 1 = argminzg(z) + ρ2∑Ii‖wi -zk + μki‖22
μk + 1i = μki + wk + 1i-zk + 1(19)
众所周知,正常评分应呈正态分布,因此本研究ADMM惩罚系数ρ使用正态函数,得到系数公式:
s′i=1MJ∑Mm=1∑Jj=1smij(20)
ρ=12πσexp(-(s′i-′)22σ2)(21)
式中,s′i为第i项评分均值,σ为标准差,评分数量为m[1,M],且MZ+,3级指标j[1,J],且JZ+.
4.2改进算法过程
判断收敛条件为迭代变量k→∞、原始变量rk及对偶变量sk→0,于是原始误差εpri和对偶误差εdual[15]如下:
εpri=ρεabs+εrelmax{‖wki‖2,‖zk‖2,0}εdual=Iεabs+εrel∑kj=1‖wki-zk‖2 (22)
‖rk‖2=∑Ii=1‖wki-‖2‖sk‖2=Iρ∑Ii=1‖wki-wk-1‖2 (23)
式中,I为指标维度,w为wi均值.为了能快速收敛,精度只需要≤0.01,因此,令绝对误差εabs=0.001,εrel=0.01.根据式(22)及式(23),得出最小求权算法如下:
input:I,ρ,εabs,εrel,Kiterationfor i=1→I do{Initial(Kiteration,z0=0.5,μ0i=0,wi0=1);
k=1;do{d=Diseulidean(wki,wi′,wi″);//欧氏距离wki=argmin_x(w*,wk1i,zk1,μk1i,d);
zk=argmin_z(wki,zk1,μk1i);
μki=Update(μk1i,wki,zk);//元值更新
Compute(‖rk‖2,‖sk‖2,εdualk);
k++;
}while(‖rk‖2>(ρεabs+εrel/2) or ‖sk‖2>εdualk) and (k<=Kiteration);
//约束条件下wi*理想最优时∑kj=1‖wki-zk‖2=1/2}
5实验与分析
5.1算法收敛性
对ADMM算法改进,简化误差判断,优选惩罚参数ρ,因此首先需要测试算法的收敛性,以保证改进算法的可靠性.根据式(22)及式(23),‖rk‖2与‖sk‖2随着k→∞迭代而逐渐收敛,则整个函数有解.因对参数采取近似处理,直接求证收敛性很困难,所以通过对‖rk‖2、‖sk‖2及wi-w*变化进行逐一测试.对连续凸函数D(wi),设εabs=0.001且εrel=0.01,式(19)中ρ与I线性变化不会影响整个迭代趋势,则设ρ=1/2,Imax=7,于是分别获得图2与图3.
从图2和图3可知,迭代后,残差‖rk‖2(k≥33)与‖sk‖2(k≥39)分别收敛到误差区间.随着k不断增加,误差区间趋于稳定,而‖rk‖2与‖sk‖2将进一步收敛,则表明该算法可以控制指标优化的精度,具备可用性.
5.2算法效率
研究在不同算法下最优值|wi-w*|的获取情况,以检验算法能力.给定L(wi,λ,σ)初值,参照文献[16]优化梯度下降算法,求各指标wi′与wi″的组合值wi.设λ0i=0.01,μ0i=0.5,则针对大数据惩罚参数ρ的结果不同,分别检验不同算法的迭代情况,如图4(A)~图4(C)所示.
随着k迭代次数的增加,wi→w*,通过实验与图4可知:1)ADMM算法比ALM算法更快速收敛;2)在给定的ε误差区间内,改进ADMM算法优于文献[16-17]ADMM算法;3)大数据评分越分散,收敛越慢,甚至可能最终难以收敛;4)针对本研究算法,惩罚参数ρ越高则收敛越快,但当ρ很大时将造成收敛震荡,从而影响收敛.总之,2种改进ADMM算法虽然具有相似的算法效率,但本研究的算法的优点是对初值不敏感且惩罚系数ρ由评分方差计算获得,由于大数据环境下需要经常变换评分规则的场景,因此,本研究的算法更适于作为综合评价的解决方案.
5.3综合评价分析
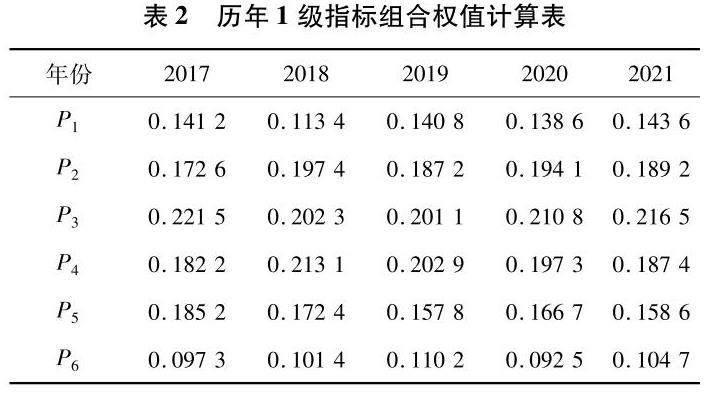
本研究用该复合权值算法对作者所在高校5年来远程在线教育系统进行评价,通过各信息系统后台评价数据计算评价指标权值,如表2所示.
此5年的1级优化权值与综合权值评分情况,如图5所示.
最终获得每年的直接累计成绩与权值成绩对比,如表3所示.
从表2、表3和图5可知:1)通过算法对权值的控制能自主体现每年实际教学能力的细节变化;2)5年来虽然教学整体评价值都获得提升,但通过权值变化发现,内容设置与过程控制是影响整个教学水平的核心因素,为接下来的教学规划调整提供了可靠依据;3)随着时间变化,辅助支持中基建与信息资源对教学效果的提升作用在逐年递减,意味着单纯的教学条件改善并不与教学水平的提高成正比;4)从权值分布看,客观权重的变化更能影响整个教学评价效果,表明在信息平台的评价选项设定上可以根据参与者偏好对客观评价指标实施调整与再计算.
总之,通过各项实验表明该复合梯度优化算法对远程在线教育评价具有实际指导作用,这不仅验证了5年来的实际教学情况,也帮助教学中发现某些被忽略的环节.
6结语
目前,各高校都在积极制定远程继续教育评价指标系统,并研发配套的统计算法.本研究通过建立3级考核指标系统,依靠高校的大数据信息平台获得评价数据,探讨组合动态模糊评价与CRITIC算法,并结合改进ADMM算法求解最优的指标权值,获取综合评价成绩.实验与实践表明,该评价系统可以真实全面体现高校继续教育实际教学状况,能直观显示在线教学过程中存在的细节问题.同时,该评价系统能减少人为干预,提高了评价的便捷性与客观性,被证明是一种适应智慧高校环境下高效的自主教学评价系统.未来的研究是通过不断改进评价算法效率及提高评估准确性来帮助各成人高校简化远程在线教学的评价过程.
参考文献:
[1]Iouliia S.Projectbased learning and evaluation in an online digital design course[J].Electronics,2021,10(6):646-646.
[2]Lyu W,Ding X,Salam A Z.Research on timeliness evaluation model of online teaching based on intelligent learning[J].Int J Cont Eng Educ Life Long Learn,2021,31(2):27-29.
[3]孙丹宇.远程教育质量评价指标体系研究[D].保定:河北大学,2020.
[4]杨晓焱.现代远程教育网络教学评价指标体系的构建研究[J].职业教育研究,2018,6(6):16-19.
[5]教育部职业教育与成人教育司.职业教育国家教学标准体系[EB/OL].(2021-03-19)[2022-05-01].http://www.moe.gov.cn/s78/A07/zcs_ztzl/2017_zt06/.
[6]河南省教育厅.河南省教育厅关于开展高等学历继续教育教学评估(2021—2025年)的通知[EB/OL].(2021-09-04)[2022-05-01].https://jyt.henan.gov.cn/2021/09-14/2312415.html.
[7]唐业喜,伍招妃,袁媛.基于CIPP模型的高校网络思政教育成效评价体系构建与解析[J].高教论坛,2021,1(1):54-57.
[8]Chang S J,Hsu C I,Lin T.Using FAHP and CBR to evaluate the intention of adoption of internet banking service:the example of web ATM[J].J Intell Fuzzy Syst,2020,39(3):2869-2879.
[9]马亚龙,邵秋峰,孙明,等.评估理论和方法及其军事应用[M].北京:国防工业出版社,2013.
[10]Dariusz F,Przemysaw J.An expert fuzzy system for management of railroad bridges in use[J].Autom Constr,2019,106(10):1056-1061.
[11]夏立荣,李润学,刘启玉,等.基于动态层次分析的自适应多目标粒子群优化算法及其应用[J].控制与决策,2015,30(2):215-221.
[12]Rau A K,Mat K M,Rizal H,et al.A modified CRITIC method to estimate the objective weights of decision criteria[J].Symmetry,2021,13(6):973-973.
[13]Banert S,Bof R I,Csetnek E R.Fixing and extending some recent results on the ADMM algorithm[J].Numer Algor,2020,86(5):1-23.
[14]Jourani A,Vilches M.Moreautosida regularization of statedependent sweeping processes with nonregular sets[J].J Opt Theor Appl,2017,173(1):91-116.
[15]Boyd S,Parikh N,Chu E,et al.Distributed optimization and statistical learning via the alternating direction method of multipliers[J].Found Trends Mach Learn,2010,3(1):19-21.
[16]王慧慧.分布式交替方向乘子法研究[D].南京:南京大学,2017.
[17]Wang C,Li C,Wang J.A modified augmented Lagrange multiplier algorithm for Toeplitz matrix completion[J].Adv Computat Math,2016,42(5):1209-1224.
(实习编辑:黄爱明)
