不等式导数问题常见题型及其解题策略

廖妍婷 杨楚锋 巫辉莹 巫阳洋 梁填 张文超

摘  要：导数与不等式、函数交汇综合是高考命题的热点.这类题型主要以选择题、解答题的形式为主，往往涉及了函数性质、导数的应用、不等式的求解等多个方面，需要学生具备较强的数学综合能力和思维能力.本文通过归纳常见的不等式导数问题并给予相应解题策略，以此来帮助学生更好地分析并掌握解决该类题型的方法和技巧.

关键词：不等式导数；函数；高考；解题策略

不等式导数问题在高考命题中占据重要地位，在高考试卷中经常以选择题和解答题的形式命题，有基础题，也有中档题，更多时候是作为“把关题”出现，承担着区分与选拔优秀学生的功能.随着教育改革的深入，高考题目灵活多变，新课标指出“基于数学核心素养的教学评价，不仅要关注学生对知识技能的掌握程度，还要更多地关注学生的思维过程”.不等式导数问题涉及化归、方程、分类讨论等数学思想，同时考查导数和不等式的基础知识，难度逐级递增、环环相扣，这对于培养学生的数学思维、逻辑推理能力具有重要意义.

1  历年高考不等式导数问题的出题特点

1.1  考查题量、题型分析

高考改革一直是近年来的热点，在“新课标，新教材，新高考”这一背景下，不等式导数问题又有哪些变化呢？下文主要从近年来高考试卷考查题量、题型方面来分析.

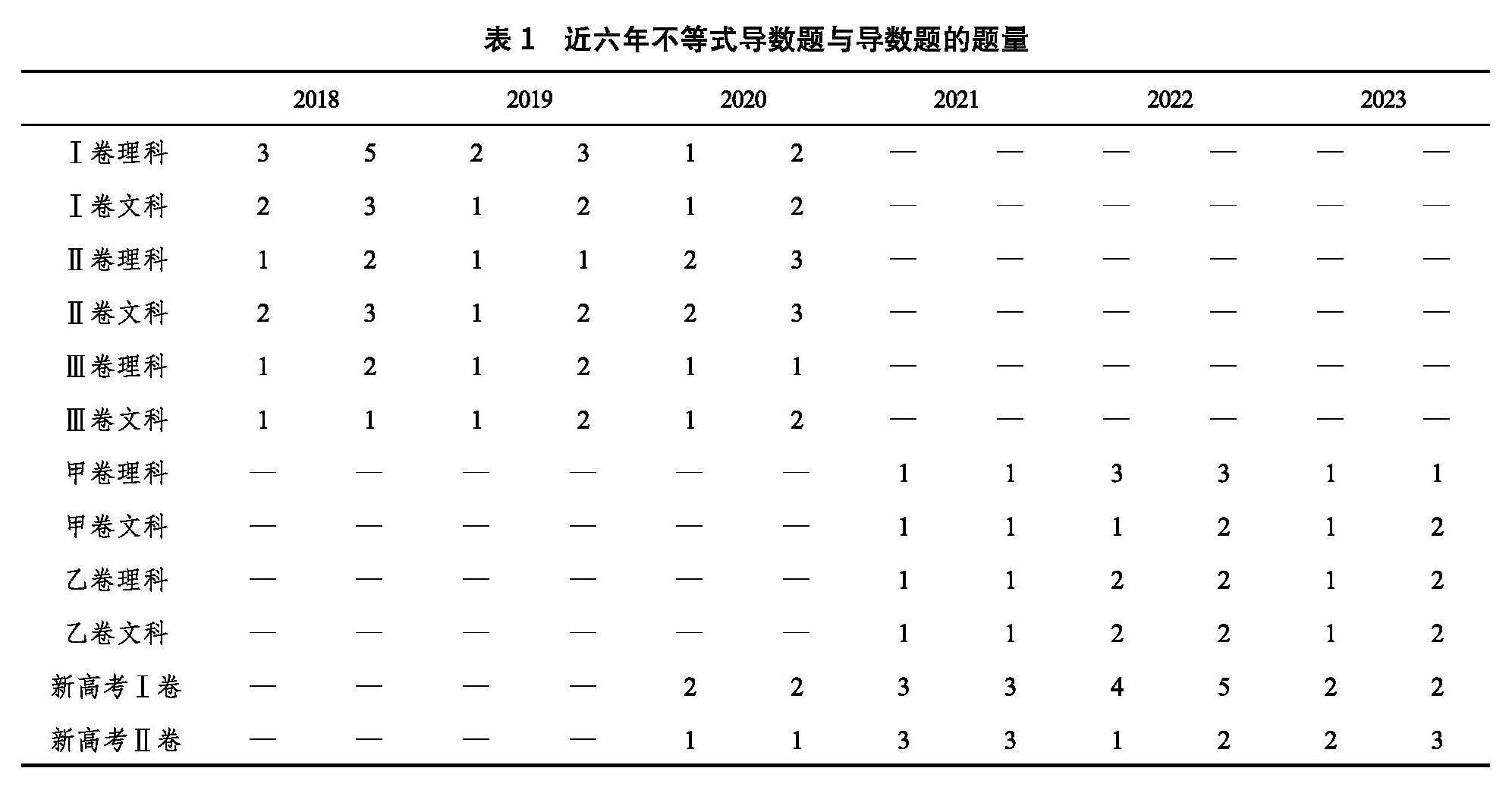
首先从考查题量方面分析.近六年全国Ⅰ卷、Ⅱ卷、Ⅲ卷，以及新高考全国甲卷、乙卷、Ⅰ卷、Ⅱ卷共38套，考查导数题共82道，其中不等式导数题共考查了59道，占比72.0%.在实施新高考前，不等式导数在导数题中考查占比为60.7%.实施新高考后，不等式导数题的比重相比旧高考有所提升.如2022年不等式导数在导数占比为81.3%，2023年不等式导数在导数占比为66.7%.具体考查题数见表1，表中每个年份的左侧为不等式导数的考查题量，右侧为导数的考查题量.

从题型方面分析.分析近几年高考试卷，不难发现导数中不等式常考问题可以总结为以下八大题型，分别是函数导数的单调性与不等式、函数零点问题、函数极值问题、证明含参不等式恒成立、不等式恒成立求参数的取值范围、存在性变量问题、数列不等式、极值点偏移.如在2022年新高考全国Ⅱ卷22（2）、22（3）分别考查了不等式恒成立求参数的取值范围和导数中的数列不等式.在2023年新高考Ⅰ卷19（2）考查了证明含参不等式恒成立，22（2）考查了函数导数的单调性与不等式以及极值问题等.

1.2  考查题型、解题策略分析

针对这八大题型，下文通过从解题方法方面剖析2022，2023年新高考Ⅰ卷、Ⅱ卷不等式导数试题并总结常用的三种解题策略.表2呈现了近几年部分不等式导数试题以及其解题方法.

从表2，我们可以清楚地看到构造函数法、切线放缩法常用于解决不等式导数问题.此外，在对其他地区的高考试卷分析中，发现在2023年全国甲卷文科20（2）可以用极值点偏移法解答，2022年全国甲卷理科21（2）的解答同样用到了极值点偏移的方法.总结归纳近几年不等式导数试题，可以发现构造函数法、切线放缩法、极值点偏移法最常用于解决不等式导数问题.

2  不等式导数问题的三种解题策略

2.1

构造函数法

例1  ^^［2023年新高考全国Ⅱ卷数学22（1）］&&证明：当0

解析：构造函数g（x）=x-x2-sinx，x∈（0，1），求导，得g′（x）=1-2x-cosx.

令p（x）=g′（x），则p′（x）=-2+sinx<0.

所以有g′（x）在（0，1）上单调递减.

故g′（x）

所以g（x）在（0，1）上单调递减.

可得g（x）

构造函数h（x）=x-sinx，x∈（0，1），求导，得h′（x）=1-cosx.

易知h′（x）>0，所以h（x）在（0，1）上單调递增.

所以h（x）>0-sin0=0，即sinx

评注：这道题目属于中档题，主要是将函数单调性和不等式证明结合起来，要求学生能够根据函数的单调性判断函数的值域，并利用函数的性质进行不等式的证明.此外还要求学生能够将所学知识综合运用，解决一些较为复杂的不等式问题.主要考查了学生的综合应用能力和逻辑思维能力.

技巧：在运用构造函数法解决不等式导数问题时，可以通过以下步骤进行解答：

（1）观察不等式的形式和已知条件，确定构造函数的形式，如已知函数f（x）在某区间内的最小值为n，则可以构造函数F（x）=f（x）-nx（其中n为某常数）；

（2）根据导数与函数单调性的关系，判断构造函数的单调性；

（3）利用单调性求解不等式.

2.2  切线放缩法

例2  ^^（2023年新高考全国Ⅰ卷数学19）&&已知函数f（x）=a（ex+a）-x.

（1）讨论f（x）的单调性.

（2）证明：当a>0时，f（x）>2lna+32.

解析：（1）先求导，再对a分类讨论，从而判断a的不同取值范围下f（x）的单调性.

（2）解法一：（切线放缩）

利用ex≥x+1.

则f（x）=a（ex+a）-x=ex+lna+a2-x≥x+lna+1+a2-x=a2+lna+1.

令g（a）=1+a2+lna-2lna+32=a2-lna-12，则g′（a）=2a-1a=2a2-1a.

令g′（a）>0，得a>22；令g′（a）<0，得0

故g（a）在0，22上单调递减，在22，+∞上单调递增.

故g（a）≥g22=12-ln22-12>0，所以f（x）>2lna+32，证毕.

解法二：（同构+切线放缩）

当a>0时，要证f（x）>2lna+32.

即证ex+lna-（x+lna+1）+12（a2-lna2-1）+12a2>0.

又ex≥x+1，故ex+lna-（x+lna+1）≥0.

又lnx≤x-1，故12（a2-lna2-1）≥0.

又12a2>0，故ex+lna-（x+lna+1）+12（a2-lna2-1）+12a2>0显然成立.证毕.

评注：这道题目主要考查了函数的单调性和极值定理的应用，以及极限的性质.在解决题目时使用切线放缩公式能达到事半功倍的效果.要求学生有较强的综合应用能力和逻辑思维能力，有助于提高学生的思维品质和解决问题的能力.

技巧：确定目标函数、构造切线函数、分析切线函数的性质（导数、单调性、极值等）、利用切线函数的性质证明不等式.以下为常见的放缩不等式.

（1）切线放缩：对于函数f（x），其导数为f′（x），则有f（x）≥f（x0）+f′（x0）（x-x0）.

（2）指数函数放缩：对于x>0，有ex≥x+1.

（3）对数函数放缩：对于x>0，有ln（1+x）≤x和ln（1+x）≥2x2+x.

（4）三角函数放缩：对于x≥0，有sinx≥x-x33！和cosx≥1-x22！.

（5）代数式放缩：对于正整数n，有1+1nn

2.3

极值点偏移法

例3  ^^（2022年高考全国甲卷理科21）&&已知函数f（x）=exx-lnx+x-a.

（1）若f（x）≥0，求a的取值范围.

（2）证明：若f（x）有两个零点x1，x2，则x1x2<1.

解析：（1）由导数确定函数单调性及最值，即可得解.

（2）解法一：（构造函数与极值点偏移）

不妨设0

又x2，1x1∈（1，+∞），f（x）在（1，+∞）上单调递增，f（x1）=f（x2），即证f（x1）-f1x1<0.

故当x∈（0，1）时，要证x1x2<1，即证明exx-lnx+x-xe1x-lnx-1x<0.

令g（x）=exx-lnx+x-xe1x-lnx-1x，则g′（x）=（x-1）（ex-xe1x+x-1）x2.

令h（x）=ex-xe1x+x-1，易得h′（x）>0.

即h（x）在（0，1）上单调递增，h（x）

则g′（x）>0，g（x）在（0，1）上单调递增，即g（x）

解法二：（对数均值不等式与极值点偏移）

令t=exx>1，则f（t）=t+lnt-a，f′（t）=1+1t>0.

所以f（t）=t+lnt-a在（1，+∞）上单调递增，故f（t）=0只有1个解.

又f（x）=exx+lnexx-a有两个零点x1，x2，故t=ex1x1=ex2x2.

两边取对数，得x1-lnx1=x2-lnx2，即x1-x2lnx1-lnx2=1.

要证x1x2x2>0.

则有lnx1-lnx2

即证lnx1x2

设t=x1x2>1，则2lnt

构造h（t）=2lnt-t+1t，t>1，则h′（t）=2t-1-1t2=-1-1t2<0.

故h（t）=2lnt-t+1t在（1，+∞）上单调递减，h（t）

故x1x2<1，即x1x2<1.

评注：本题属于难题，通过设置综合性的导数不等式问题和较为复杂的情境，重视基于数学素养的关键能力的考查，具有较好的选拔功能，考查了学生灵活应用函数、不等式思想解决复杂问题的能力，对直观想象能力和逻輯推理能力也有较高的要求.

3  总结与展望

不等式导数问题在高考命题、数学研究中占据核心地位，对数学的发展和应用具有重要意义.解决这类题型对于提高学生的数学素养和解决问题的能力都具有重要的价值.

本文通过对标历年高考试卷，归纳出八大题型，即函数导数的单调性与不等式、函数零点问题、函数极值问题、证明含参不等式恒成立、不等式恒成立求参数的取值范围、存在性变量问题、数列不等式、极值点偏移，并总结出三大解题策略——构造函数法、切线放缩法、极值点偏移法，此外对这三类方法分别进行研究并总结做题技巧.

希望学生能熟练掌握解决不等式导数问题的技巧，学习其数学思想，领略数学魅力，也希望各位数学教育工作者能提出更多更精妙的解决不等式导数问题的策略，教学相长，共同进步！

参考文献

［1］ 李笑竹.高中数学学科核心素养的培养途径探究［J］.科学咨询（教育科研），2021（1）：171.

［2］ 中华人民共和国教育部.普通高中数学课程标准（2017年版）［M］.北京：人民教育出版社，2018.

［3］ 刘灏.利用构造法解决极值点偏移问题——以2022年高考全国甲卷理科数学第21题为例［J］.数理化解题研究，2023（25）：40-42.

［4］ 赵林.合理运用放缩法 有效破解证明不等式难题［J］.数理化解题研究，2021（19）：36-37.

［5］ 周小锋.利用导数证明不等式的技巧策略［J］.中学生数理化（高考数学），2023（5）：21-23.

［6］ 郑坚帜.数学建模视角下与导数有关的不等式问题妙解路径［J］.中学数学研究，2023（10）：47-50.

［7］ 敖羚峰.高中数学导数试题分析、解题错误与教学对策研究［D］.上海：华东师范大学，2021.