基于函数大概念的中考数学试题研究

盛昊灿 夏瑜琦

摘  要：函数大概念引领函数问题解决的过程.本研究基于对中考函数内容的分析，并借鉴大概念的层级体系，建构基于函数大概念的中考数学试题分析框架，以此为核心说明在数学问题解决过程中大概念的重要作用.以期强调函数大概念在函数课堂教学中的重要地位.研究以中考函数试题为例，提炼三个结论，并给出三点教学启示，以期对数学问题解决和课堂教学有所助益.

关键词：函数；大概念；中考数学；试题研究

大概念的引入积极促成了教育学的变革与进步.大概念已经不仅仅是一个简单词汇，它背后潜藏着一个意义的世界，它超出了一个普通概念的应有内涵与外延，作为一种深刻思想、学说的负载体，已成为“思想之网”的联结枢纽.［1］中考试题具备有效性、可靠性、教育性与教学导向性.［2］函数作为数学学科的大概念之一，是初中数学的重要学习主题［3］，也是中考数学重要的组成内容.基于函数大概念的视角对中考数学试题进行分析有助于发挥中考以评促教和以评促学的作用，帮助大概念融入数学课堂教学，具有广泛的现实意义.

1  基于函数大概念的研究框架的建构

1.1  函数大概念的内涵

张翰提出大概念是联结学科知识的纽带，大概念的表现形式是多样的，其可以是以单词或短语表达的核心概念，也可以是以句子表达的学科观点和理论.［4］刘徽认为大概念可以被界定为反映专家思维方式的概念、观念或论题，它具有生活价值.［5］众多学者给出了自己对大概念的理解，其中应用较为广泛的是如图1所示的大概念层级体系.［6］

在四个层级中，学科视角所属的两个层级较贴近日常教学并易理解其内涵，就函数而言，学科层级包含了一次函数的概念、性质等事实性知识和学科概念（第一层级），也包括一次函数、函数性质等内涵更为广泛的核心概念（第二层级）.跨学科视角下的层级更是如火如荼地被教育学者所讨论，函数作为描述“变化”的数学内容，其中便有较多的跨学科背景，常与物理、化学和体育等学科基础知识相结合.而第四层级则指向学科内容中内隐的思想方法，其涉及学科本质的方法论、情感态度和价值观的讨论.基于此，可以给出如图2所示的函数大概念层级体系，并以此作为本研究函数大概念的内涵.

1.2  研究框架的建构

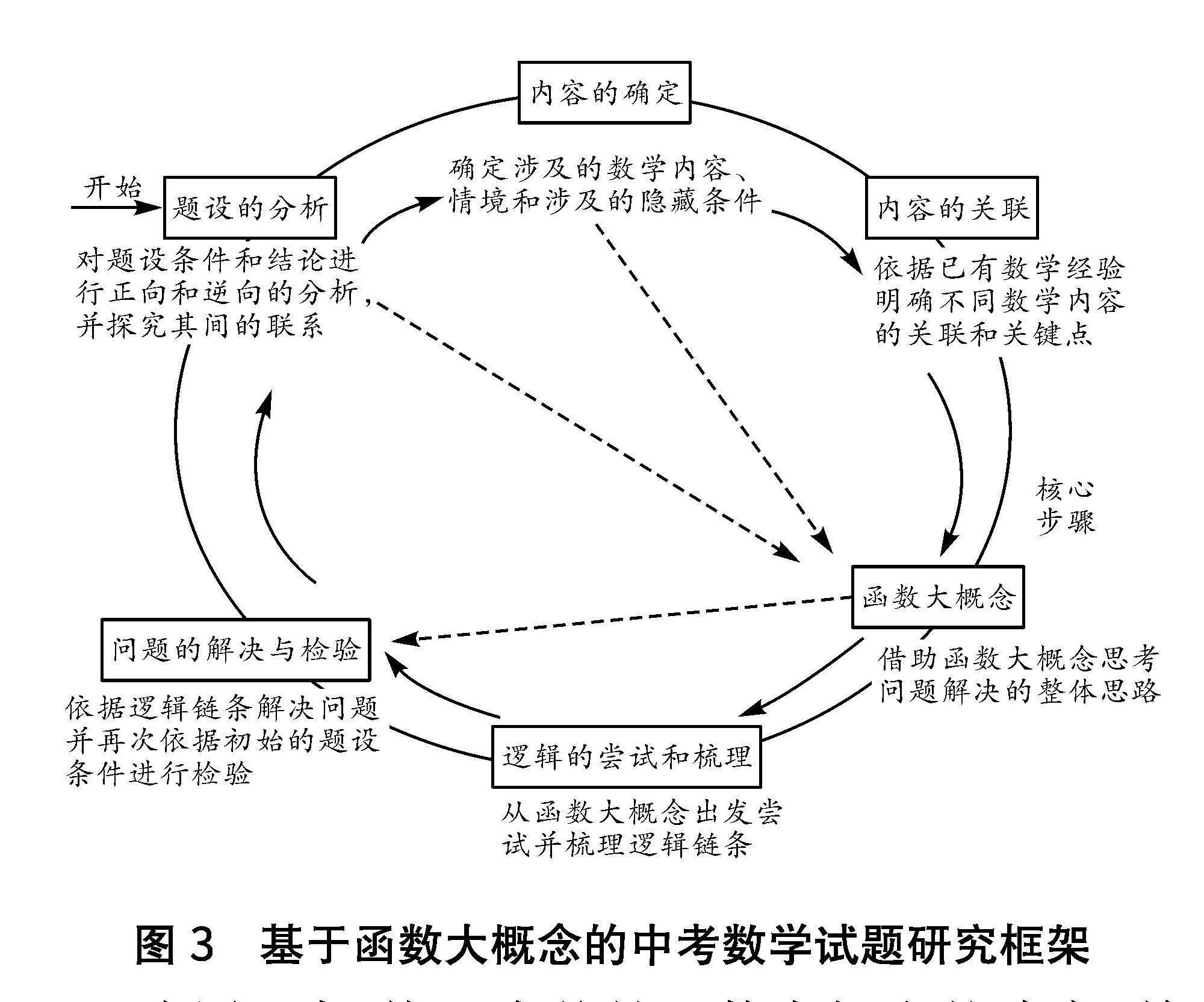
函数大概念的内涵明确了需要从系统的、整体的和关联的视角分析中考函数试题.依据从理解题目到给出假设，再运用归纳和演绎推理解决问题的基本思考路径，可以构建如图3所示的研究框架，研究框架由六个环节循环构成.

在图3中，核心步骤是函数大概念的确定，并以此作为整个循环的循环节点，其余的五个步骤都可以回归到对函数大概念的环节.框架图中各个环节并非需要依次进行，每一个环节完成后都可以重新回归到函数大概念的环节，并借助函数大概念的层级体系进行思考与检验.

2  中考数学试题研究例析与结论

2.1  理清逻辑起点和关键点，为问题解决过程提供动力和保障

例1  ^^（2023年杭州中考数学第22题）设二次函数y＝ax2+bx+1（a≠0，b是实数）.已知函数值y和自变量x的部分对应取值如下表所示：

x…-10123…

y…m1n1p…

（1）若m＝4，①求二次函数的表达式；

②写出一个符合条件的x的取值范围，使得y随x的增大而减小.

（2）若在m，n，p这三个实数中，只有一个是正数，求a的取值范围.

2024年第3期复习考试

复习考试2024年第3期

分析  从题设条件的分析出发，可以发现该题主要涉及二次函数“本身”图象和性质的内容，并没有与其他数学内容相关联.函数大概念更多的作为基础知识、核心概念与一般化的思想方法起着帮助回忆数学内容和熟练运用函数知识的作用.为问题解决过程提供逻辑起点和保障.

对第（1）小题进行分析，其主要涉及学科知识层级.该题可以直接用较为熟悉的代入式子列方程的路径求得其一般式的系数并确定范围，也可以先通过函数大概念中关于对称性、单调性的性质找到其对称轴作为突破口，即可减少运算量解决问题.对第（2）小题的分析则需要一般性的函数思想方法出发，函数大概念更多起着一般化地看待一类问题的思想作用，利用函数的性质的核心概念，借助对称性求得m=p，即只有n为正.以此明晰问题解决过程的逻辑起点和关键点，即可列出不等式组求解.

2.2  关联不同主题和内容领域知识，使问题解决过程具备结构性和整体性

例2  ^^（2023年金昌中考数学第27题）如图4，抛物线y＝-x2+bx与x轴交于点A，与直线y＝-x交于点B（4，-4），点C（0，-4）在y轴上.点P从点B出发，沿线段BO方向匀速运动，运动到点O时停止.

（1）求抛物线y＝-x2+bx的表达式；

（2）当BP＝2时，请在图4中过点P作PD⊥OA交抛物线于点D，连接PC，OD，判断四边形OCPD的形状，并说明理由；

（3）如图5，点P从点B开始运动时，点Q从点O同时出发，以与点P相同的速度沿x轴正方向匀速运动，点P停止运动时点Q也停止运动.连接BQ，PC，求CP+BQ的最小值.

分析  该题涉及函数主题下的不同内容，分别是二次函数与一次函数.函数常与几何内容相结合，如圆和四边形等，不同函数之间的联系也是中考考查的重点.此题需要以函数思想方法为统领，从题设条件出发，借助函数大概

念

的层级体系，找到两个函数之间的联系.同时以学科层级为着力点，整体地、联系地看待两个函数之间的联系，进而求解.

第（1）小题，借助函数的定义，利用待定系数法将B点坐标代入抛物线y＝-x2+bx中，即可求解.第（2）小題，需要从题目条件出发，挖掘函数的性质核心概念下的基础定理，通过作辅助线把几何结构或者定理成立需要的条件进行补全，求出PD的长，

证明PD＝OC，PD∥OC，利用一组对边平行且相等的四边形是平行四边形即可得证.第（3）小题，找出变化过程中的不变性，函数大概念中的转换思想强调解决变化问题往往需要借助不变的量，故完成符合条件的图象后，可以构造全等三角形，CP+BQ的最小值即可以转换为定长的线段，根据勾股定理求出长度即可.

2.3  把握跨学科背景与概念，让问题解决过程贴近生活和现实

例3  ^^（2023年北京中考数学第25题）某小组研究了清洗某种含污物品的节约用水策略，部分内容如下.每次清洗1个单位质量的该种含污物品，清洗前的清洁度均为0.800，要求清洗后的清洁度为0.990.

方案一：采用一次清洗的方式.

结果：当用水量为19个单位质量时，清洗后测得的清洁度为0.990.

方案二：采用两次清洗的方式.

记第一次用水量为x1个单位质量，第二次用水量为x2个单位质量，总用水量为（x1+x2）个单位质量，两次清洗后测得的清洁度为C.记录的部分实验数据如下.

x111.09.09.07.05.54.53.53.03.02.01.0

x20.81.01.31.92.63.24.34.05.07.111.5

x1+x211.810.010.38.98.17.77.87.08.09.112.5

C0.9900.9890.9900.9900.9900.9900.9900.9880.9900.9900.990

对以上实验数据进行分析，补充完成以下内容.

（1）选出C是0.990的所有数据组，并划“”；

（2）通过分析（1）中选出的数据，发现可以用函数刻画第一次用水量x1和总用水量x1+x2之間的关系，在平面直角坐标系xOy中画出此函数的图象；

结果：结合实验数据，利用所画的函数图象可以推断，当第一次用水量约为    个单位质量（精确到个位）时，总用水量最小.

根据以上实验数据和结果，解决下列问题：

①当采用两次清洗的方式并使总用水量最小时，与采用一次清洗的方式相比、可节水约    个单位质量（结果保留小数点后一位）；

②当采用两次清洗的方式时，若第一次用水量为6个单位质量，总用水量为7.5个单位质量，则清洗后的清洁度C    0.990（填“＞”“＝”或”＜”）.

分析  本题是一道跨学科背景下的函数问题.故在思考本题时需要借助函数大概念中的跨学科层级，明确跨学科概念在问题解决过程中的作用，回忆已有的生活经验，使问题解决过程贴近生活经验和现实情境，不会感到陌生与被动，从而解决问题.

对（1）和（2）小题，根据表格中数据描点连线即可做出函数图象，再结合函数图象找到最低点求解.这里需要借助函数大概念学科层级中的函数图象的核心概念对该题跨学科背景进行理解，意识到需要采用描点法解决问题.剩下两题主要考查跨学科概念的理解，从生活实际出发，借助函数图象求解即可.

3  教学启示

3.1  明确函数大概念在问题解决中的核心地位

问题解决需要有严密的逻辑链条，但在实际考查中，可以发现学生往往对逻辑起点和关键点无从下手，在得知完整的解决过程后又幡然醒悟，感叹问题解决的巧妙.此问题出现的主要原因是学生对函数大概念的内涵和层级体系并不明晰，且对自己所处的困境并无察觉，此类情况下，教师必须明确函数大概念在问题解决过程中的核心地位，以此强调仅仅借助学科层级

能解决的

问题是极为有限的，让学生在学习中开阔思维，不局限于基础知识的“狭小胡同”.

3.2  明晰函数大概念在问题解决中的引领作用

现有的问题解决教学范式强调先于知识前提出问题，以问题为学生学习知识的驱动器，一改课堂教学先有知识后解决问题的路径，但是在整个过程仍旧需要明晰大概念在整个过程中的引领作用，其基础知识和核心概念可以迟于问题的提出，但是函数思想等却引领问题提出的过程.

3.3  加强函数大概念在问题解决中与现实经验的联系

问题解决并非埋头苦干，而是源于自己的生活经验，跨学科背景和概念等不仅仅从课堂中获得，更需要明确的是，生活经验也是学习过程的一个重要环节.函数大概念所具有的一大特征即是与生活密切相关，在问题解决过程中，教师需要从生活中提取真正存在的问题，而非凭空杜撰，才能落实函数大概念引领下的数学课堂教学.

参考文献

［1］赵康.大概念的引入与教育学变革［J］.教育研究，2015，36（2）：33-40.

［2］吴增生.初中数学毕业考试命题变革的思考与实践［J］.数学通报，2021，60（1）：41-51.

［3］缪琳.基于“SEC”一致性分析的初中数学考查研究［D］.福州：福建师范大学，2018.

［4］张翰.“大概念”：一个不容忽视的课程新理念［J］.思想政治课教学，2019（6）：31-33.

［5］刘徽.“大概念”视角下的单元整体教学构型——兼论素养导向的课堂变革［J］.教育研究，2020，41（6）：64-77.

［6］李刚，吕立杰.科学教育中的大概念：指向学生科学观念的获得［J］.自然辩证法研究，2019，35（9）：117-123.