指向核心素养的高中数学深度学习探究
2024-06-07毛世勤
毛世勤

【摘要】在核心素养导向下,深度学习的实施,可以让学生更好地认识数学学科的本质,提高学生关键能力和思维品质.文章基于核心素养的视角,提出了包括更新教学理念、把准实际学情、创设问题情境、师生双向互动、创设有效问题等高中数学深度学习的策略,旨在通过这些策略帮助学生更好地理解和应用数学知识,培养他们的数学思维和解决问题的能力,获得适应终身发展的品质和素养,从而让数学核心素养在深度学习课堂上落地生根.
【关键词】高中数学;深度学习;数学核心素养;品质和素养
高中数学核心素养是高中数学课程评价的重要目标,是落实立德树人根本任务的重要举措,也是培养新时代创造性人才的重要方向.数学核心素养是在解决数学问题的实践中,逐渐养成的數学品格和综合性能力.培养学生数学核心素养在提升学生数学实践能力,发展学生理性思维,丰富学生数学知识储备等方面有着非常重要的现实意义.深度学习强调学习过程中形成的能力,其与核心素养中的“关键能力”“必备品格”有着密切的联系.研究深度学习,并将其实践到高中数学课堂教学中,不仅可以优化学生的知识结构,提高学生分析和解决问题的能力,而且可以提升适应学生终身发展的品质和素养.以下是笔者就深度学习的内涵,及深度学习的落实谈的几点自己的认识,若有不足,请指正.
一、深度学习的内涵
深度学习也称为深层学习,其强调主动理解与批判接受,强调数学本质与数学思想方法,它是发展学生高阶思维,提高学生分析和解决问题的重要途径.深度学习是浅层学习的延续和深化,它是一种主动的、探索式的、理解式的学习方式.深度学习可以让学生积极主动地、批判地学习新知识和新思想,有效提高学生主体思维的参与,让学生在高阶思维中主动进行知识的建构、转化和迁移,以此让学生获得可持续学习的能力,促进学生数学核心素养的落实.
深度学习与深度教学密不可分,深度学习的发展离不开教师的精心设计和耐心指导.在数学教学中,教师应发挥好课堂领导者的作用,结合教学内容和学生学情精心设计和规划,让学生在其引导下积极地互动,以此通过不同思维的碰撞与情感的交流引发高阶思维,促进学生深度学习的达成.
另外,深度学习强调学生的学习过程,其可有效弥补浅层学习中存在的碎片化、浅表化、浮躁化等缺陷,充分调动学生学习的主动性、积极性,实现教师、学生和教学内容的高度统一,实现教学相长.同时,深度学习为学生提供了自主探索的空间,可以促进学生的深度参与、深度思考和深度感悟,有效促进学生数学核心素养的培养.
二、实现深度学习的有效策略
在新课改背景下,高中数学课堂的教学方式、教学手段、学习方式等都发生了许多变化,但是教学中仍然存在着一些问题,如教学中忽视知识的前后联系,使学生的知识结构呈现零散性和碎片化;教学中片面地追求速度,使学生对知识的理解局限于识记,缺乏对知识与技能背后数学思想方法的感悟;教学中忽视了学生的主体价值,影响学生参与课堂的积极性.为了改变这一局面,高中数学课堂学习必须走向“深度学习”.笔者结合教学实践浅谈几点实现深度学习的有效策略,供参考!
(一)更新教学理念,激活学习动力
在数学学习的过程中,若过多地强调智力因素对数学成绩的影响,而忽视非知识因素的影响,则很容易让学生因为感觉数学难学而放弃学习数学.要知道,数学学习不仅需要智力因素的积极参与,也要非智力因素的积极配合,只有帮助学生树立正确的学习态度,才能让学生全身心地投入数学学习中,从而让深度学习真正地发生.另外,只有让学生深度投入,才能让学生充分体验学习的乐趣,从而激活学生学习动力,让学生逐渐走上乐学、会学之路.
例如,在讲解等比数列通项公式时,教师可以改变传统的“讲授+练习”的教学模式,以趣味性问题为线索,诱发学生深度思考,开展深度学习.问题如下:将一张厚度为0.1mm的报纸对折2次,这叠纸多厚?如果将报纸对折30次,这叠纸大概多厚呢?如果对折100次呢?教学中,教师提供时间让学生思考、猜想、探索,鼓励学生大胆说出自己的想法.在学生做出种种估计后,教师给出答案,学生发现自己的猜想与实际结果相差甚远,由此让学生产生强烈的探究欲,进而全身心地投入等比数列通项公式的学习中,这有效激发了学生学习的内驱力,促成深度学习.
(二)把准实际学情,确定发展目标
数学课堂教学的主体是学生,若想调动学生的主体性和积极性,教师的精心设计必不可少.可见,深度学习离不开深度教学,而深度教学离不开教师的精心设计和规划.教师作为课堂教学的组织者,要立体式地分析学生的学习,把准学情,找准“最近发展区”,精准定位深度学习的学习目标,激发学生内驱力,促进深度学习的发生.教学中,教师要了解学生的“过去”,分析学生已有的知识储备、认知经验和思维水平,预估通过深度学习能够掌握的知识,提升的能力与素养,以此制定促成高阶思维的课程目标.
例如,在教学“对数函数”时,若教师直接将定义、图像、性质等呈现给学生,让学生理解和识记,则学生可能很难与指数函数建立联系,这样不仅会影响新知的学习效果,而且会影响学生认知体系的建构.基于此,在实际教学中,教师应先引导学生回顾指数函数的相关内容及学习过程,这样既可以了解学生对指数函数及其图像、性质的掌握情况,又能有效沟通二者的内在联系,让学生通过类比顺利地理解和掌握对数函数的特性.在探索对数函数的性质时,教师可以借助图像引导学生观察、抽象,如教学中可以让学生探索y=loga(x+b)(a>0且a≠1)与y=logax(a>0且a≠1)图像之间的关系.这样以学生的已有知识和已有经验为线索,引导学生进行类比分析,可以使抽象的知识变得更加生动,使学生对对数函数的建构过程更加清晰,有助于深度学习的发生.同时,在此过程中,新、旧知识的对比,有利于实现知识、经验和方法的迁移,有利于学生分析和解决问题能力的提升,促成高阶思维的课程目标的达成.
总之,数学是一门逻辑性较强的学科,在课堂教学中,教师要重视引导学生将相关知识联系起来,以此加深学生对新知的理解和掌握,优化原有的认知结构,发展学生数学核心素养.
(三)创设问题情境,提升数学体验
数学知识是抽象的,若课堂教学仅依赖于教师的讲授,则很容易使学生产生厌学情绪,影响其参与课堂的积极性、主动性,这样深度学习也就无从谈起.为了改变这一局面,让学生全身心地投入数学学习中,教师不妨创建情境,将抽象的数学知识置于生动的问题情境中,让学生在情境互动中理解知识的本质与意义,让深度学习自然而然地发生.
例如,在教学“等比数列前n项和公式”时,为了提升学生的数学体验,让学生全身心投入和沉浸其中,教师根据学习内容的特点、教学目标的要求和学生思维发展水平创设了如下情境:国王想打赏象棋发明者,于是问他想要些什么.象棋发明者说:“我不要金银珠宝,只要您在棋盘的第一个小格赏我1粒麦子,第二个小格赏我2粒麦子,第三个小格赏我4粒麦子……以此类推,将棋盘中的64个格子摆满.”试想,如果你是国王,你会答应他的要求吗?这样通过创设情境,有效地激发了学生的探究欲.为了解决这一问题,教师又从学生已有知识和已有经验出发,精心设计如下问题进行引导:
(1)依据要求,你能算出每小格棋盘的麦粒数吗?
(2)观察数字,你发现了什么规律?它是等差数列还是等比数列呢?
(3)如果让你计算一共有多少粒麦子,你想怎么算?
(4)你能帮国王算出麦粒数吗?如果你是国王,你会答应吗?
(5)请结合以上探究过程总结归纳等比数列前n项和公式.
教学中,教师先是创设有趣的情境激发学生的探究欲,然后巧妙地设计问题引导学生将其与等差数列相关知识相类比,由此开启学生的高阶思维,帮助学生顺利推导出“等比数列前n项和公式”.通过经历以上探究过程,学生充分体验了成功的喜悦,真实感受了数学在解决现实问题中的价值,这有利于发展学生的逻辑推理、数学运算等核心素养.
(四)师生双向互动,建立学习共同体
教学是教与学的交往、互动,没有交往、没有互动,也就没有教学的发生.教学可以理解为是师生相互交流、相互补充、相互启发的过程,也是师生双方相互成就的过程.在深度学习过程中,教师要为学生搭建一个互动交流的平台,让学生主动表达自己的所思、所想,构建以学为中心的学习共同体,形成学习的内动力和积极的学习心态,让学生学会学习.同时,教学中教师要树立“学生”意识,善于从学生的视角思考和解决问题,为学生的思维牵线搭桥,让学生学有所获,从而提升课堂教学质量.
例如,在双曲线的应用中,教师给出了这样一道题:已知A,B两地相距900米,一枚炮弹在某地发生爆炸,B地听到爆炸声2秒后,A地才听到爆炸声,若声速是340米/秒,试求爆炸点可能的位置.学生审题后,未能与双曲线模型建立联系,解题时遇到障碍.为了帮助学生突破障碍,教师与学生进行互动交流.
师:本题的关键条件是什么?
生1:B地听到的爆炸声比A地听到的爆炸声早2秒.
師:若将其转化为数学问题,你想到了什么?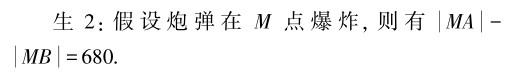
师:非常好,若M在A,B的连线上,则会是什么图形呢?
由此通过“对话”,课堂“慢”了下来,学生逐渐认清了问题的本质,找准了解题方法,有效地突破了解题难点,增强了学生的解题信心.
深度学习强调主动理解,主动探索、主动感悟,因此当学生遇到障碍时,教师不要急于讲授,应该适当放慢速度,通过“对话”为学生的思维搭桥,诱发学生深度思考,从而让深度学习真正发生.
(五)创设有效问题,促进深度思考
问题是思维的起点,是发展学生高阶思维的加速器.深度学习离不开深度思维,因此在课堂教学中,教师要创设一些能够触及学生心灵的、凸显问题本质的、具有一定深度的问题,以此撬动学生的思维,促进学生深度思考.
例如,已知圆的方程为x2+y2=r2,点M(x0,y0)为圆上一点,求经过点M的切线方程.
在教师的指导下,学生积极思考,得到该切线方程为:x0x+y0y=r2.在此基础上,为了增强学生的批判意识,教师设计了以下形同质异的变式题.
变式1 已知点M(x0,y0)是圆x2+y2=r2内的一点(点M异于圆心),试判断直线x0x+y0y=r2与圆的位置关系.
从解题反馈来看,很多学生受原题影响,看到直
这样有了前面问题的铺垫,学生摆脱“想当然”的束缚,冷静思考,通过迁移和转化顺利地解决了问题.
基于此,在实际教学中,教师要适当为学生创设一些“陷阱”,诱导学生犯错,以此通过经历析错、纠错等过程加深学生对知识的理解,增强学生批判意识,凸显问题本质,实现深度学习.
总之,深度学习离不开深度教学.在实际教学中,教师应从教学实际出发,创设符合学生认知水平,能够诱发学生思考,激发学生探究欲的教学活动,以此让学生主动参与到课堂教学活动中,使学生学习逐渐走向深入,促进学生发展核心素养.当然,深度学习是一个长期的过程,需要学生进行长期坚持不懈的努力,因此教师要正视这个客观规律,不断更新教学观念,优化教学结构,加强“学生”意识,努力构建学习共同体,不断提高教学质量,切实提升学生数学核心素养.
【参考文献】
[1]郭兴甫.浅谈数学教学中构建问题情境的策略[J].课程教材教学研究(中教研究),2004(Z5):55-56.
[2]王延全.挖掘课本习题资源提升数学课堂效率[J].数学大世界(教师适用),2012(10):67.
[3]杜金梅.试论高中数学课堂教学深度学习的有效实施[J].新课程(下),2018(11):7.
[4]张晓禄.高中数学:从“知识教学”走向核心素养培育[J].数学教学通讯,2021(36):44-45.
[5]洪明磊.促进深度学习的高中数学教学策略研究[J].数学学习与研究,2021(24):127-128.
