凸显角本质的学习路径研究：巩固、运用角本质

黄旭冉 林卓然 张芳铭 许佳敏 巩子坤

【作者简介】黄旭冉，小学数学教师，主要研究方向为数学教育；林卓然，中学数学教师，主要研究方向为数学课堂教学；张芳铭，在读硕士研究生，主要研究方向为数学教育；许佳敏，中学数学教师，主要研究方向为数学课堂教学；巩子坤（通讯作者），教授，博士生导师，主要研究方向为基础教育数学课程改革的理论与实践。

【基金项目】2023年度浙江省哲学社会科学规划课题“基于认知发展模型的义务教育教科书编写质量提升研究”（23NDJC265YB）；2021—2022年度浙江省高校重大人文社科攻关计划项目“建设高质量教育体系背景下义务教育教科书编写质量提升路径研究”（2023GH005）

【摘 要】凸显角本质的“角的初步认识”单元整体教学路径分为三个课时。本文研究第三课时，即巩固、运用角本质的学习路径。文章通过教学实践与研讨，得到完善的学习路径：由转动引入锐角、直角和钝角，动静结合比较角的大小，巩固角本质；通过分类活动认识直角、锐角和钝角，并呈现不同开口方向的直角，体会直角的特殊性；转动活动角，运用角本质进一步感受锐角、直角和钝角之间的大小关系。由此，提出教学建议：用“转动”一以贯之直角、銳角和钝角的学习；借助分类活动，展示不同开口方向的直角，感受直角的特殊性。

【关键词】角的本质；角的分类；学习路径；直角；锐角；钝角

一、研究缘起

为解决当前“角的初步认识”教学中未凸显角本质的问题，本研究提出了凸显角本质的“角的初步认识”单元整体教学，共分为“初识角的概念”“体验、认识角本质”“巩固、运用角本质”三个课时。第一课时“初识角的概念”借助分类和动手创造，帮助学生认识角的特征，掌握角的概念（第一课时的研究文章刊载于本刊2024年第3期）；第二课时“体验、认识角本质”设置了动静结合的角的大小比较任务，通过关注“转动的多少”，帮助学生体验、认识角本质（第二课时的研究文章刊载于本刊2024年第4期）。在认识了角的概念，体验了角的本质后，如何运用角本质来认识具体的角，是本文要回答的问题。笔者在先前研究的基础上，进一步提出本文的研究问题：如何运用角本质实现对角的分类（认识直角、锐角和钝角）？如何围绕角本质的巩固与运用构建学习路径？

二、研究设计

我们继续在YH小学二年级的甲、乙两个班中开展教学实践，由教师W按照本研究设计的学习路径进行备课、授课。研究方法与研究流程同“初识角的概念”“体验、认识角本质”，不再赘述。以下主要介绍后测问卷及数据处理。

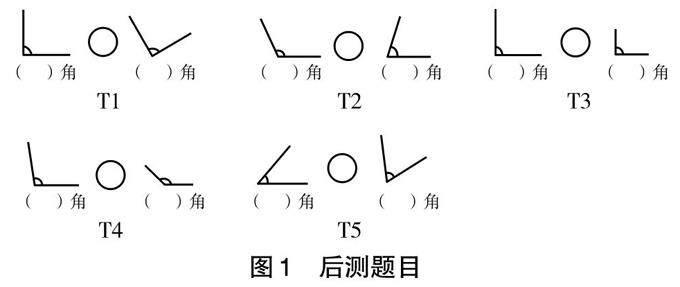
后测题目一共有5道小题（如图1）。对于给出的“转动的多少”、“边长的长短”或“开口的方向”不同的5组角，学生首先需要判断这些角属于哪类角（锐角、直角、钝角），然后对角的大小进行比较。

教师对学生的作答情况进行赋分，正确记1分，错误记0分，最后统计总分。

三、研究结果与分析

（一）学习路径的设计与实施

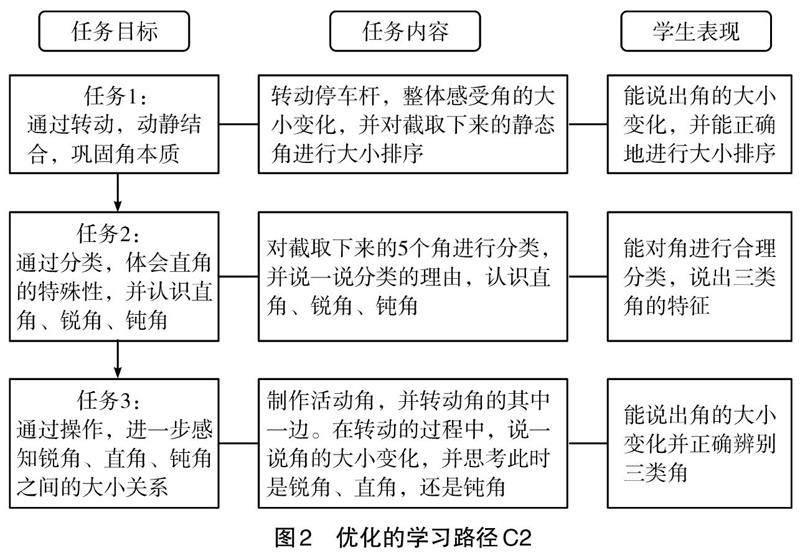
为探究得到完善的学习路径，本研究经历了多次教学设计、两次教学实践及多次教学研讨。限于篇幅，本文只呈现在乙班开展的优化的学习路径C2，如图2所示。

其中，任务1包含2个子任务。

子任务1.1：慢慢转动停车杆，整体感受角的大小变化。

在第二课时“体验、认识角本质”中，停车杆模型是体现角本质为“转动的多少”的良好载体，可以沿用。但需要注意的是，相较于真实的停车杆，此时的模型更类似于由停车杆模型抽象得到的“转动模型”，转动的幅度由直角扩大到平角，这样才会在旋转过程中出现锐角、直角和钝角。教师缓慢转动停车杆，引导学生在动态、连续的过程中整体感受角的大小变化，对角的本质进行再认识与复习。同时，也将锐角、直角和钝角置于一个整体结构中，以便后续引入。

子任务1.2：截取停车杆转动过程中形成的角，进行大小排序，并说明理由。

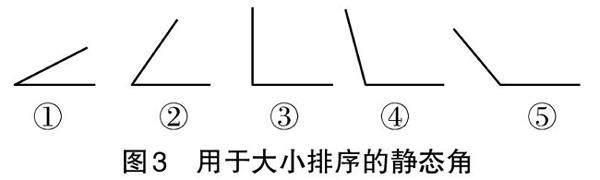
将停车杆转动过程中的动态角截取下来形成静态角，分别为2个锐角、1个直角、2个钝角（如图3），并进行大小排序。学生结合动态的转动过程，对截取下来的静态角进行大小排序，动静结合，以此巩固对角本质的认识。

任务2包含3个子任务。

子任务2.1：对图3中的5个角进行分类，并说一说分类的理由。

为引入直角，教师最早设计的环节是请学生直接思考哪个角最特殊。但学生心中对“特殊”的理解是千差万别的，回答因人而异。因此，这样的问题设计显然缺乏指向性。在第一课时“初识角的概念”中，学生通过分类活动，提炼出角的特征。优化后的学习路径C2也设计了图形的分类活动，通过辨别图形特征，帮助学生初步形成对不同角的认知。学生通过对停车杆转动过程中截取下来的角进行分类，能够体会到直角是锐角与钝角的分界线，以此凸显直角的特殊性。

在分类过程中，学生主要给出了三种分法：①②、③④⑤；①②③、④⑤；①②、③、④⑤。通过分析、比较这三种分类情况，教师引导学生关注产生分歧的源头，即③号角，并针对其特殊性展开讨论。子任务2.1的课堂实录如下。

师：比较这三种分类情况，它们有什么不同？

生：对③号角的分类不一样。

师：为什么会不一样？

生：它最特殊。

师：特殊在哪里？

生：①、②号角是向里倒的，④、⑤号角是向外倒的，只有③号角是直直地站着。

师：③号角就是我们今天要学习的直角。

在学生认识直角并感受其特殊性后，教师引出锐角和钝角的概念：像①②这样，比直角小的角叫锐角；像④⑤这样，比直角大的角叫钝角。

子任务2.2：寻找教室中的直角。

学生在教室的各处（如黑板、书柜、窗框、粉笔盒等）可以找到符合直角特征的角。由此，教师引导学生用数学的眼光观察现实世界，同时搭建抽象概念与现实具体的桥梁，加深学生对直角的认识。

子任务2.3：利用锐角和钝角的学具，感受它们为何如此命名。

教师利用硬纸板制作的锐角和钝角学具，引导学生通过触觉体验，感受锐角和钝角为何如此命名，由此加深對锐角和钝角的认识。锐角摸起来是尖锐的，赋以“锐”字；钝角摸起来不是尖锐的，赋以“锐”的反义词——“钝”字。

任务3：制作活动角，并转动角的其中一边。在转动的过程中，说一说角的大小变化，并思考此时是锐角、直角，还是钝角。

任务3需要同桌两人合作完成。首先，两人共同利用小棒制作活动角。其次，一人将活动角的一边固定并缓慢转动另一边，当转动停止时，另一人需要说出此时的角相较于上一刻的角的大小变化情况，以及此时的角是锐角、直角，还是钝角。重复若干次后，双方交换。这样“制作动态角、转动动态角、感知动态角”的活动过程，是学生体验与思考的过程，即运用角本质理解锐角、直角和钝角之间的大小关系，并体会大小不同的锐角和钝角。

综上，任务1主要由“转动”巩固对角本质的理解并引入不同类型的角；任务2通过对任务1的素材进行分类，先认识特殊角——直角，再通过比较认识锐角和钝角；任务3通过转动活动角，并运用角本质进一步感知锐角、直角和钝角之间的大小关系。由此，“转动”贯穿直角、锐角和钝角的学习过程，促进了学生对角本质、角特征的系统理解。同时，直角、锐角和钝角的学习过程也与角本质的巩固、运用过程此呼彼应，相得益彰。

（二）学习路径的教学效果与分析

如前文所述，本研究首先在甲班开展了假想的学习路径C1的教学，结合专家建议与甲班后测情况，继而在乙班开展了优化的学习路径C2的教学。以下对甲、乙两个班的后测情况进行定量分析，并结合典型回答，验证学习路径得到了改进。甲、乙两个班的得分情况如图4所示。

比较甲、乙两个班的成绩，发现乙班学生在T1、T4和T5上的正确率均高于甲班，在T2和T3上的正确率与甲班保持相等。对甲、乙两个班学生的后测得分进行独立样本t检验。通过分析整体得分可以发现，乙班学生比较角大小和辨析三类角的正确率显著提高，对角本质的认识更加深刻。通过分析T1、T2和T3得分可以发现，甲、乙两个班的学生均能意识到“转动的多少”是影响角大小的本质因素，以及排除“开口的方向”这一非本质因素。在特殊情况下（如T3，两个角均为直角），也能排除“边长的长短”这一非本质因素。两个班在这方面的认知水平不存在显著性差异。通过分析T4得分与T5得分可以发现，乙班学生相较于甲班更能在一般情况下排除“边长的长短”这一非本质因素（如图5），并且对于锐角、直角和钝角的概念区分更加清晰（如图6）。由此说明，优化的学习路径C2能有效帮助学生认识直角、锐角和钝角，并巩固、运用角本质。

需要注意的是，优化的学习路径C2仍存在可完善之处。直角是认识锐角和钝角的基础，因此，学生对直角特殊性的感受显得尤为重要。学生将直角特殊性理解为“直直的”，但实际上，直角的“直”体现在一条边与另一条边的位置关系是垂直的，即相对位置的“直”。然而学生对于相对位置关系的感受较弱，因此，对直角特殊性的理解容易存在偏差。教师可以通过以下任务引导学生体会直角的“直”是相对位置的“直”。首先，教师展示开口方向不同的若干个直角（如图7），询问学生这些是否是直角。其次，教师将直角的开口方向统一，询问学生调整方向后的角是否还是原来的角，以及这些角是否是直角。这样的概念性变式，即变换同类事物的非本质特征以突出事物的本质特征［1］，将有利于学生对直角特殊性的体会。

据此修改得到完善的学习路径C3。由于实施优化后的学习路径C2在很大程度上满足了预期的学习目标，且最终完善的学习路径C3与C2相差不大，故不再详述。

四、结论与建议

（一）结论

本研究通过多次教学设计、两次教学实践及多次教学研讨，最终得到了完善的“巩固、运用角本质”学习路径：首先从停车杆的转动出发，让学生巩固对角本质的理解，引出不同类型的角；其次通过分类和比较得到直角、锐角和钝角；最后通过制作活动角，让学生在转动过程中亲身经历角的变化。研究表明，本研究设计的学习路径能有效帮助学生巩固、运用角本质，同时实现对角的正确分类（认识直角、锐角和钝角）。

（二）建议

1.用“转动”一以贯之直角、锐角和钝角的学习

“转动”体现了角的本质，因此，可以用“转动”一以贯之直角、锐角和钝角的学习，使得直角、锐角和钝角的学习过程整体化、本质化。如在停车杆转动的过程中，截取出锐角、直角和钝角的素材；通过动静结合进行大小排序，为后续分类活动认识直角、锐角和钝角做铺垫；通过转动活动角，进一步感知锐角、直角和钝角的大小关系。

2.借助分类活动，展示不同开口方向的直角，感受直角的特殊性

分类思想在小学数学的各个领域有着广泛的应用，它具有培养学生有条理地思考、发展学生良好思维品质等作用。［2］因此，分类活动是认识图形特征的重要手段。首先，教师可以通过分类活动，对比锐角的“向里倒”和钝角的“向外倒”，引导学生体会直角的“直”。其次，教师通过展示不同开口方向、看似不“直”的直角，经由开口方向的调整重新变“直”，引导学生体会直角的“直”在于一条边相对于另一条边的“直”。由此，学生由浅入深地感受直角的特殊性。

参考文献：

［1］鲍建生，黄荣金，易凌峰，等. 变式教学研究（续）［J］. 数学教学，2003（2）：6-10，23.

［2］姚美芳. 分类在认识图形中的教育价值［J］. 小学数学教育，2021（6）：9-11.

（责任编辑：罗小荧）