一种应用于旅行商问题的莱维飞行转移规则蚁群优化算法

丁增良 陈珏 邱禧荷

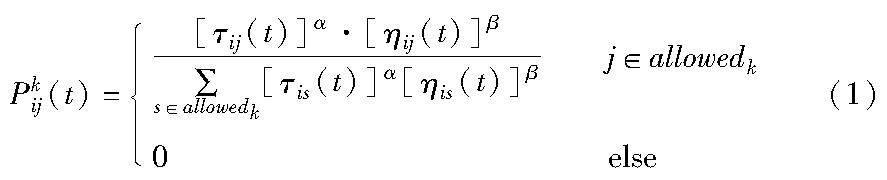
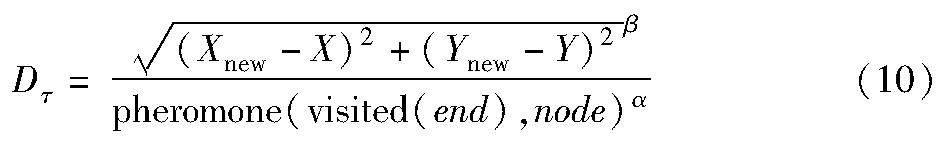
摘 要：针对旅行商问题（TSP）提出了一种基于莱维飞行转移规则的蚁群优化算法。该算法结合了基于莱维飞行和蚁群系统算法（ant colony system，ACS）的转移规则，形成了一种动态权重的混合转移规则，该策略能够有效地帮助算法跳出局部最优，增强全局搜索能力。此外，随机多路径优化3-opt策略通过随机抽取部分路径与当前最优路径组合，增加算法的多样性。当算法陷入停滞时，采用信息素平均随机重置策略重置路径上的信息素浓度，有助于算法跳出局部最优。实验结果显示，所提算法在处理多个不同规模的TSP实例时，与最优解的误差保持在3%以内，证明了该算法在TSP中具备出色的收敛性和避免陷入局部最优解的能力。

关键词：蚁群算法；旅行商问题；莱维飞行；3-opt

中图分类号：TP18   文献标志码：A    文章编号：1001-3695（2024）05-020-1420-08

doi： 10.19734/j.issn.1001-3695.2023.09.0450

Ant colony optimization algorithm based on Lévy flight transfer rule for solving traveling salesman problem

Abstract：This paper proposed an ant colony optimization algorithm based on Lévy flight transition rule for the TSP. The algorithm combined the transition rule based on Lévy flight and ACS， and formed a dynamic weight hybrid transition rule， which could effectively help the algorithm escape from local optima and enhance the global search ability. In addition， the random multi-path optimization 3-opt strategy increased the diversity of the algorithm by randomly extracting some paths and combining them with the current optimal path. When the algorithm stagnated， it used the pheromone average random reset strategy to reset the pheromone concentration on the path， which helped the algorithm escape from local optimal. The experimental results show that the proposed algorithm keeps the error within 3% compared with the optimal solution when dealing with multiple TSP instances of different scales， proving that it has excellent convergence and ability to avoid falling into local optima in the TSP problem.

Key words：ant colony optimization; traveling salesman problem（TSP）; Lévy flight; 3-opt

0 引言

旅行商問题是组合优化领域中的一个典型问题，在现实生活中有许多应用［1］。比如，在物流配送领域可用于优化物流配送路线，减少送货时间和成本；在网络通信中优化数据传输路线，减少传输时延和网络拥塞等。

旅行商问题目前主要由启发式算法进行求解，研究人员提出了众多启发式算法试图解决TSP。文献［2］介绍了六种常用的启发式算法，包括最邻近算法、遗传算法（genetic algorithm，GA）、模拟退火算法、禁忌搜索算法、粒子群算法（particle swarm optimization，PSO）和树木生理学优化算法，并比较了各算法的性能、准确性和收敛性。

许多研究人员在这些经典启发式算法的基础上进行改进，以解决旅行商问题。比如，陈加俊等人［3］提出一种基于探索-开发-跳跃策略的单亲遗传算法；禹博文等人［4］提出了一种引入动态分化和邻域诱导机制的双蚁群优化算法；Zhang等人［5］在2022年提出了一种具有跳跃基因和启发式算子的遗传算法；Roy等人［6］提出了一种基于多亲交叉技术的新型模因遗传算法；lhan等人［7］提出了一种基于列表的交叉算子模拟退火算法。

另一方面，研究人员对许多新型的启发式算法进行改进以应用到旅行商问题。Gharehchopogh等人［8］在哈里斯鹰优化算法（Harris hawk optimization algorithm）的基础上提出了一种使用随机密钥编码生成路线的方法来解决TSP，该方法能够针对各种TSP实例找到最优或近似最优解。

Zhang等人［9］提出了一种适用于TSP的离散鲸鱼优化算法，首先将鲸鱼优化算法进行离散改进以适应TSP，同时为了增强算法的能力，增加了自适应权值、高斯扰动和变邻域搜索策略，提高了算法的种群多样性和全局搜索能力，实验表明该算法能够有效解决TSP问题。

人工蜂群算法是一种模仿蜜蜂采蜜行为的群体智能优化算法，其基本思想是将蜂群分为采蜜蜂、观察蜂和侦察蜂三类，分别承担不同职责，分工合作对问题进行计算求解。Khan等人［10］改进了该算法使其适应离散问题，通过修改多个更新规则和K-opt操作来解决对称和非对称的旅行商问题（TSP），与文献中的其他对比方法相比，该算法的准确性、效率和一致性方面表现良好。

麻雀搜索算法是一种受麻雀觅食和反捕食行为启发的群体智能优化算法［11］。离散麻雀搜索算法（discrete sparrow search algorithm，DSSA）是Zhang等人［12］在其基础上改进的离散版本。DSSA使用轮盘选择生成初始解，使用基于顺序的解码方式来更新麻雀的位置，使用结合高斯突变和交换算子的全局扰动机制来平衡勘探和开发，以及使用2-opt局部搜索来提高解的质量。通过实验验证，该方法在解决TSP时有较好的竞争力和鲁棒性。

在众多经典的和新型的启发式算法中，蚁群算法（ant co-lony optimization，ACO）具有较好的优化效果。ACO是一种具有群体智能和随机性的元启发式算法，已被用于处理许多综合优化问题［13］。该算法最早是由Colorni等人［14］参考蚂蚁在其群体和食物来源之间寻找路径的行为而提出的，后来的研究以此为基础，出现了各种各样的变体。Lee［15］提出了一种将蚁群优化算法和遗传算法相结合的算法，并应用于解决旅行商问题。Cheng等人［16］提出了一个基于分解的多目标蚁群优化的框架，以解决双目标旅行商问题。Ban［17］提出了一种结合蚁群算法、遗传算法和邻域下降与随机邻域排序的混合算法，以解决旅行商问题。Dahan等人［18］采用飞行蚁群算法（dynamic flying ant colony optimization，DFACO）来解决旅行商问题的方法。Yang等人［19］提出了一种基于博弈的新型蚁群优化算法用于解决旅行商问题，其在多个实例上表现出优越的效果。Dorigo等人［20］指出，近年来研究ACO算法的主要方向之一是将其与其他元启发式方法相融合。

本文从另一个角度出发，对蚁群算法转移规则进行了研究和改进。本文算法是基于最大最小蚁群算法（max-min ant system，MMAS）的改进。MMAS作为ACO的变体，与原始ACO的不同之处在于：MMAS只允许使用最佳解决方案来更新信息素轨迹，并使用一种机制来限制信息素值的范围。这种设计使得MMAS能够更有效地利用搜索历史，从而避免陷入次优解。尽管通过这些策略可以避免过早收敛，但同时也可能导致搜索过程中多样性和探索性的丧失，从而使算法陷入局部最优解。因此，为了解决MMAS的这些局限性，本文基于MMAS提出了一种新的蚁群算法，该算法引入了莱维飞行的混合转移规则，以更好地平衡开发和探索，提高算法的性能。

本文采用了多种改进策略以增强蚁群算法的性能。首先，提出了一种混合转移规则的改进策略，包括基于贪心、基于莱维飞行和基于概率的转移规则，并为每种规则分配了不同的权重因子，用于控制每种转移规则被选择的概率。为了应对基于贪心规则容易导致蚂蚁陷入局部最优解的问题，本文采用动态权重线性递减的方式来调整基于贪心规则的权重，这种动态权重的混合转移规则不仅继承了MMAS算法的优点，还有效地弥补了MMAS算法的不足之处。其次，本文通过优化3-opt技术，提出了一种具有随机路径优化的3-opt策略来减少回路的总长度。最后，为了避免算法陷入局部最优解，本文提出了信息素平均随机重置策略，这一策略有助于保持算法的多样性，从而更有可能發现全局最优解。

实验结果表明，本文提出的改进算法在求解TSP实例时能取得较好的实验结果，对于不同规模的TSP实例其求解精度能保持在一个较优的范围，与最优解的误差始终保持在3%以内。同时相比于传统的蚁群算法和其他最新的蚁群算法，本文算法也能取得更好的实验结果，证明了这些改进策略的共同作用提高了蚁群算法在解决问题时的性能和稳定性。

1 相关工作

1.1 最大最小蚁群算法

MMAS作为ACO的一种，是由Stützle等人［13］在传统ACO基础上提出的改进算法。本文算法以最大最小原则的蚁群优化算法为基础，算法模拟生成m只蚂蚁，并随机地将它们分配到n个城市中。在t时刻，蚂蚁k从城市i转移到城市j的概率Pkij（t）为

其中：τij表示城市i到j路径上的信息素浓度；ηij表示从城市i到j的期望启发因子；allowedk表示蚂蚁k下一步可以去的城市集合；参数α和β则用于调整在计算概率时信息素和启发信息的相对权重。

蚂蚁在经过的路径上释放一定的信息素，用来与其他蚂蚁交流信息。当所有的蚂蚁都完成了一次完整的路径后，根据每只蚂蚁所走过的路径长度来更新信息素。更新信息素的公式为

其中：ρ表示信息素挥发率；Δτij表示信息素增量，信息素增量有多种计算方法，一般选择将式（3）作为增量的计算方式；Lk表示蚂蚁在本次周游中所走过的路径长度；Q为一个正常数，一般设为1。随后，检查更新后的信息素的值是否在［τmin，τmax］，如果信息素的值大于上界，就将其值改为上界值，如果信息素的值小于下界，就将其值改为下界值。其中，τmin表示信息素浓度的下界，τmax表示信息素浓度的上界。

1.2 转移规则

转移规则在蚁群算法中具有关键作用，它决定了蚂蚁选择下一个节点的方式。在解决旅行商问题中，选择适当的下一个节点对算法性能至关重要。根据不同蚁群算法的变体，转移规则也会有所不同。其中一种常见的是基于概率的转移规则，它根据边上的信息素浓度和启发式信息计算节点被选中的概率。然后，根据轮盘赌法来随机选择一个节点作为将要访问的对象。这种转移规则的具体计算公式如式（1）所示。轮盘赌法的基本思想就是依据城市的选择概率将轮盘划分为多个扇区，同时随机生成的随机数大小对应着图1中的某个位置，落入哪个扇区，就代表选中哪个城市。

不同的转移规则各有利弊。基于概率的转移规则能够保持一定的随机性和多样性，有助于避免陷入局部最优解，但可能导致收敛速度较慢。此外，由于轮盘赌法依赖于生成的随机数大小，这种随机性可能引入一定不确定性，影响算法的稳定性和可靠性。为弥补算法的不足，Dorigo等人［21］提出了一种伪随机比例转移规则。

该规则是根据式（1）基于概率的转移规则以及基于贪心的转移规则融合而成，其中p为（0，1）的随机数，用于平衡探索和开发。当p≤q0时，使用基于贪心的转移规则，根据式（4）中的第一个式子选取具有最大概率的节点，以提高算法的收敛速度。当p>q0时，采用式（1）代表的另一种转移规则，并通过轮盘赌法选择下一个节点，以增强算法的探索性能。尽管伪随机比例规则更好地平衡了探索和开发，但是改进后的蚁群算法仍然存在可能陷入局部最优的问题。为此，本文提出了一种动态权重的混合转移规则，除了前文提到的两种方法融合形成的伪随机比例规则，还提出了一种基于莱维飞行的转移规则。

1.3 莱维飞行

莱维飞行是由法国数学家Paul Lévy于20世纪初提出的一种随机过程。在莱维飞行过程中，每一步的步长服从莱维分布，该分布具有重尾分布的特性，即尾部概率较高。因此，莱维飞行通常以较小的步长进行移动，但偶尔也会发生较大幅度的跳跃。莱维飞行的小步跟踪特点能够帮助算法增强局部搜索能力，使算法能够在较优的区域内充分探索，提高解的质量。此外，莱维飞行的长距离跳跃特性扰动了稳定路径，有助于算法跳出局部最优解，进一步增加了解的多样性。自然界有些现象也呈现出莱维飞行的特征，例如，在某些动物的迁徙中会展现出类似于莱维飞行的现象，表现为在长距离的迁徙过程中，会突然地、不规则地改变方向和位置。

图2展示了莱维分布、高斯分布和柯西分布的随机数分布情况。为了更直观、简单地观察随机数的分布特性，本文采用了二维分布图的方式进行展示。图中的X坐标轴表示三种分布生成的数值，而Y坐标轴则表示随机生成的数值。从图2可以看出，正态分布呈现出典型的对称分布特征，其尾部相对较轻。而另外两种分布则表现出非对称的特点，属于重尾分布。相对于柯西分布，莱维分布在尾部区域更为分散，且包含更多数值。这表明在旅行商问题等应用中，莱维分布更适合作为改进算法的策略，有助于算法在更广泛的区域内进行局部搜索，跳出局部最优解，增强算法的探索能力。

式（5）是用Mantegna方法生成随机数的公式，Mantegna方法通过正态分布生成随机步长，这些步长遵循莱维分布，形成了莱维飞行的路径。

其中：β是一个参数，控制了莱维分布的形状，一般取值为1.5；μ和ν是服从正态分布的随机变量，具体如下：

因此，通过借鉴具有莱维飞行现象动物的运动方式，一些学者将其应用到各类优化算法中。例如，Zhong等人［22］设计了一种基于白鲸运动规律的元启发式算法，称为白鲸优化算法（beluga whale optimization，BWO），用于求解各类优化问题。

鉴于莱维飞行的良好特性，它也被用于蚁群算法的改进，Bansal等人［23］提出了一种改进的莱维分布杂交蚁群算法，并在一些基准函数上与标准蚁群算法进行了比较。Liu等人［24，25］对转移规则阶段进行了改进，引入了莱维飞行机制，该方法通过动态参数调整，增加了解的多样性和搜索范围。然而，现有的莱维飞行蚁群算法的研究着重于参数的动态调整，缺乏对旅行商问题中如何选择下一个节点的方法的改进。对此，本文提出了一種全新的基于莱维飞行TSP的转移规则。

2 算法描述

本文从三种从不同的角度对算法提出了改进策略。动态权重的混合转移规则用于更好地平衡探索和开发，加快算法收敛速度的同时增强算法跳出局部最优的能力，提高算法的全局搜索能力；随机多路径优化3-opt策略优化局部的路径，降低陷入局部最优的可能性；信息素平均重置策略帮助算法在陷入停滞情况时跳出局部最优；然后以MMAS算法为基础框架，将这三种改进策略融合其中，形成了一个先进的蚁群算法。

2.1 动态权重的混合转移规则

本文在莱维飞行的基础上对蚁群算法的转移规则进行改进，提出了一种全新的转移规则。通常，莱维飞行被广泛应用于处理连续问题，如式（7）所示，对算法输出数据的处理中采用了Lévy函数，以促使算法在连续问题领域避免陷入局部最优解。

然而，由于数据是离散化的，不能直接将该公式用于旅行商问题的蚁群算法转移规则阶段，所以需要对其进行改进。

为了模拟旅行商在二维空间中的移动过程，假设旅行商从当前城市出发，按照随机方向和一定的步长前进，以达到新的坐标位置。该过程可以表示为

其中：角度θ由随机数生成；step是通过Mantegna方法实现的莱维飞行的步长。由图3可知，经过式（8）计算，得到了一个新坐标点（Xnew，Ynew）。然而，新坐标点未必与城市节点重叠，因此需要进一步处理新节点坐标，以确定算法下一个节点的位置。

next_node=nearest_node（Xnew，Ynew）（9）

next_node是通过输入新节点坐标获取到下一个最优城市节点的方法。该方法以新坐标（Xnew，Ynew）为圆心，以式（10）的计算结果为半径，在城市集合中寻找数值最小的城市。如图3所示，当使用传统方法计算下一个城市时，可能会选择移动到city 2。但是当使用基于莱维飞行的转移规则时，可能会选择city 1。

其中：X、Y表示未访问节点集合中每一个节点的坐标值；pheromone表示当前路径上的信息素水平；visited（end）表示刚刚访问过的节点。算法1是next_node方法的伪代码，该方法可以有效地指导蚂蚁选择下一个节点。

算法1 使用新坐标获取下一个移动节点

为了平衡算法的探索性和开发性，本文将基于莱维飞行的转移规则与基于贪心的转移规则和基于概率的转移规则进行组合，创造一种新的混合转移规则。

前文已经介绍了莱维飞行的特性，它模拟了莱维飞行中的长距离跳跃，并在全局搜索中起到跳出局部最优解的作用，提高了算法的探索范围和多样性，增强了全局搜索能力。基于贪心的转移规则则利用局部最优信息，选择具有最大概率的节点作为下一个移动的节点，加快了算法的收敛速度，能够快速收敛到局部最优解，增强了局部搜索能力。传统的基于概率的转移规则则使用轮盘赌法，根据节点上的信息素浓度选择下一个节点，它在动态权重的混合转移规则中起到平衡开发和探索的作用，通过信息素浓度的引导和一定程度的随机性，有助于维持算法的多样性和全局搜索能力。

在实际执行过程中，算法需要根据当前情况智能地选择下一个节点的转移规则。然而，不同的转移规则在不同情况下可能具有不同的优势，因此需要动态调整这些规则的选择，以确保算法的高效性和全面性。为此，根据不同的权重系数确定了三种转移规则的选择概率，并在算法迭代过程中动态调整了基于贪心的转移规则的权重系数，以避免算法过早收敛到局部最优解。如式（11）所示本文采用的动态权重的混合转移规则。

其中：r是一个随机数；w1、w2、w3分别为基于贪心的转移规则、基于莱维飞行的转移规则和基于概率的转移规则的权重因子。为了在算法早期快速达到一个较优的解，并在后期减小基于贪心的转移规则的权重，避免陷入局部最优，本文对w1权重因子采用了随算法迭代而线性递减的方法。

在选择递减策略时，有线性递减和非线性递减两种方法。线性递减方法会随着算法迭代次数的增加，按照线性比例逐渐减小权重，这种方法可以在算法中保持一种相对稳定且简单的探索与开发之间的平衡。尽管线性递减不能像非线性递减方法那样根据算法的不同迭代阶段来调整权重减少的速度，比如加速或减缓收敛速度，但它能够更稳定地控制权重的变化，避免突然的权重变化对整体算法性能造成的不稳定性影响。与此同时，非线性递减方法也会增加算法在混合转移规则方面主导的开发与探索的复杂性，可能需要增加参数进行实验调整，并对算法的探索与开发的影响进行详细分析。综上，本文选择了线性递减的方式。

2.2 局部优化策略

2.2.1 随机多路径优化3-opt策略

3-opt是旅行商问题中常见的优化策略，它通过断开路径中不相邻的三个节点之间的连接，并尝试以不同的方式重新连接这些节点，以改善路径的质量。在3-opt策略中，涉及到三个节点的断开和重连操作，共有八种不同的连接方式，如图4所示，包括初始的路径连接方式，如图4所示。針对不同的连接方式，计算它们所对应的路径长度，并选取路径长度最短的一条连接路径作为新的路径方案。

为了提高算法整体性能，本文提出了一种随机路径优化的3-opt算法。该算法的步骤如下：

a）对当前迭代中的所有路径按长度进行排序，取最短路径作为该策略的优化路径之一。

b）从剩余路径中随机抽取若干条路径与上一步的最短路径形成待优化路径集合。

c）对集合中的每条路径执行3-opt操作，即通过重新连接路径段来生成更优的新路径。

d）将优化后的路径加入到当前迭代的所有路径集合中，并重新排序，选出当前的最优路径。

该算法通过随机抽取部分路径与当前最优路径组合，增加了搜索空间的多样性，降低了算法陷入局部最优解的可能性，增强了全局搜索的能力。

2.2.2 信息素平均随机重置策略

尽管采用了各种策略避免算法陷入局部最优策略，但仍然存在陷入局部最优解的风险。为了平衡蚁群算法的探索和利用能力，并避免算法陷入局部最优解，本文为算法增加了信息素重置策略。信息素重置策略是在算法运行一定次数的迭代后执行，旨在调节路径上的信息素的浓度，引导蚂蚁搜索更好的方向。

本文设计了一种新的信息素重置策略——信息素平均随机重置策略。算法伪代码如算法2所示。该策略的设计基于路径上信息素的平均值计算，并将其与（0，1）的随机数相乘，以实现信息素的重置，这种策略不是每次迭代都进行，而是当算法停滞一定的迭代次数才能触发，这样既保留了信息素重置策略的优势，又避免了过度重置信息素导致的负面影响。该策略的创新性在于平均重置的思想，并不是直接将信息素初始化为一个固定的值，而是通过路径信息素重置为（0，1）的随机数乘以先前计算的平均值。这在一定程度上保持了原本的环境信息，并引入了一定程度的随机性，有助于避免在随后的算法迭代中陷入局部最优解，如式（12）所示。

T=rand（citys，citys）×τave（12）

算法2 信息素平均随机重置策略

总的来说，信息素平均随机重置策略在蚁群算法中起到了关键作用，有助于算法在迭代停滞时跳出当前的局部最优状态，保持在搜索空间的多样性，防止早熟收敛，从而更有可能发现全局最优解。此外，算法中设定的迭代次数触发条件确保了重置不会频繁发生，避免了该策略对正常的算法优化产生过度影响。

2.3 LFACO算法流程

LFACO（Lévy flight-based ant colony optimization algorithm）在MMAS的基础上进行改进，主要对转移规则、3-opt策略和信息素重置策略等方面进行改进，算法流程如图5所示。当满足终止条件时，程序将结束，并输出最短路径。

3 实验与结果分析

本文的仿真环境为MATLAB 2021b，CPU为AMD Ryzen 7 5800H with Radeon Graphics，16 GB内存，操作系统为Windows 11。为了验证LFACO的优化性能，本文从TSPLIB中选择了多个城市规模在51～439的TSP实例进行测试。在TSPLIB的实例中，大部分使用欧几里德距离来计算城市之间的距离，这种计算方式根据城市的横坐标和纵坐标计算城市之间的直线距离，简单快速，降低了计算负担。因此，本文也采用了欧几里德距离来求解TSP。

3.1 实验参数设置

算法参数的取值是影响元启发式算法获得良好性能的重要因素。其中，LFACO有以下几个固定值，蚂蚁数量m决定了算法的搜索规模，一般取10～50；全局信息素挥发因子ρ决定了信息素的挥发速度，一般在0～1；局部信息素挥发因子ξ；最大迭代次数iter是算法运行结束的一个标志；信息素启发因子α代表信息素对选择下一城市的影响程度；期望启发因子β大小反映了蚁群在搜索最优路径时先验性和确定性因素的作用强度，其值越大，选择局部最优路径的可能性就越大。

信息素启发因子和期望启发因子是一对高度相关的参数，它们决定了算法在全局最优性能和快速收敛性能之间的平衡。因此，这两个参数的影响和作用是相互协调、紧密相关的，为了获得优质的最优解，算法必须在这两个参数之间找到平衡。为了达到这个目标，本文进行了对比实验，分别使用不同的信息素启发因子和期望启发因子值作为算法的输入参数，选取eil51和pr226两个TSP实例进行求解。根据图6显示，当α=1，β=5时，实验解的质量较高，因此选择这组参数值作为信息素启发因子和期望启发因子的最优值。

为了确定合适的动态权重混合转移规则的相关参数，本文针对三种不同的转移规则，通过一系列的实验测试，采用不同的权重因子，对性能进行评估。为了保证实验的可靠性，确保实验结果的差异是不同权重因子对算法性能造成的影响，本文保持算法的其他参数恒定，仅对权重因子大小进行调整。此外，为了提高研究的普适性，减少实验的误差与偏差，本文选用了st70、rat99和pr152三种TSP测试实例。

为了综合评价三种转移规则对算法的收敛性能和最优解质量的影响，本文采用了最优迭代次数Topt和最短路径长度Lbest作为评价指标。将这两个指标按照一定的权重相加，得到一个表征综合性能的分数，该分数越小，表示性能越好，具体如式（13）所示。图7展示了不同转移规则组合下的综合性能分数变化，其中纵坐标是综合性能分数，横坐标的每组数字分别代表基于贪心的转移规则（w1）、基于莱维飞行的转移规则（w2）和基于概率的转移规则（w3）的权重。由于蚁群算法本身具有随机性，每次求解的结果会有一定的波动，所以将三次求解的结果求平均值，得到最终确定的权重因子为w1=0.6，w2=0.2，w3=0.2。

score=0.8×Lbest+0.2×Topt（13）

综上所述，LFACO算法的参数设置如表1所示。

3.2 动态权重的混合转移规则分析

为验证动态权重的混合转移规则的适用性，对LFACO与不包括动态权重的混合转移规则的改进算法，以及去除其他两种改进策略只保留混合转移规则的改进算法进行了实验对比分析。其中，去除改进策略后的替代策略均采用与经典MMAS算法相同的策略。实验以不同规模大小的数据集为例，分别为ch150、pr152、pr264和rat575。相比于其他两种改进算法，LFACO通过式（11）更好地平衡了开发和探索。

图8为三种算法的收敛对比，从图中可以看到，曲线是呈不断下降的趋势，说明这三种算法都能有效地寻找TSP实例的最优解。在算法迭代的初期，三种算法可以快速收敛到一个较小值附近，这归因于三种算法所包含的基于贪心的转移规则。与式（4）代表的伪随机比例规则相比，混合转移规则在引入基于莱维飞行的转移规则后具备了更出色的全局搜索能力。在算法前期，例如图8 （a）在迭代200次以内时，LFACO的收敛曲线可能暂时处于劣势，但是最终这四张图中的LFACO都求得了三者之中最优的收敛值。

在图8 （c）中，迭代次数100～300，即使改进算法具有信息素平均随机重置策略，仍陷入局部最优并未跳出。与此同时，LFACO和去除其他两种改进策略只保留混合转移规则的改进算法通过混合转移规则持续收敛。

总体来看，图8（a）～（d）的收敛曲线最终结果基本都是LFACO大于去除其他两种改进策略只保留混合转移规则的改进算法，大于不包括混合转移规则的改进算法，体现了混合转移规则的优越性。尤其对于大规模城市数据集，LFACO的表现明显优于其他两种算法，其曲线始终保持在较低位置，充分证明了LFACO在全局和局部搜索能力方面的出色表现。

3.3 LFACO实验结果

LFACO的实验结果如表2所示。在表中，BKS代表了每个TSP实例的十个解决方案中的最优解长度。best和worst分别表示算法在每个TSP实例的十个解决方案中的最佳和最差实验结果，average则表示了这十个解决方案的平均值。Mr表示平均误差率，它反映了average与BKS之间的相对误差；Er表示误差率，它反映了best与BKS之间的相对误差。

从表2可以看出，eil51、eil76、kroA100、kroB100和kroB150的实验结果均达到了BKS。对于其他数据集，尽管并未达到BKS，但是误差均小于3%。图9显示了部分LFACO计算的TSP实例的最优解决方案。总的来说，LFACO对于TSP表现出了较好的性能。

3.4 与其他算法的对比

3.4.1 与经典蚁群算法對比

表3为经典算法ACS和MMAS与LFACO对比实验时的参数设置。图10为与ACS的多样性对比。表4对比了LFACO与传统的ACS和MMAS在不同规模的TSP实例上的优化性能，其中粗体数字代表每个类别中的最佳结果。从表中数据可以明显看出，LFACO在除了pr439的best结果之外，在其他所有的类别中都显著优于ACS和MMAS。而MMAS在pr439的best结果中，仅比LFACO多优化了68个距离单位。因此，本文可以得出结论，LFACO在大多数的TSP实例上都能够获得更优质的解决方案，相比于传统的ACS和MMAS，具有更强的优化性能。

如图11所示，可以清晰地观察到LFACO在所选的TSP实例中能够快速地收敛到最优解或接近最优解，并且表现出良好的稳定性。除了eil76实例外，LFACO的收敛曲线都位于其他两种算法的曲线之下。在eil76实例中，MMAS的曲线在前200次迭代内短暂地位于LFACO的下方，但随后被LFACO超越。在tsp225实例中，由于城市规模的扩大，在大约400次迭代之间，LFACO经历了一段停滞期。然而，由于信息素平均随机重置策略的应用，算法成功摆脱了局部最优解，最终获得了更小的最优解。综上所述，图11表明LFACO具有强大的搜索能力和较快的收敛速度。

接下來将LFACO与传统的MMAS的多样性进行比较。本文使用信息熵作为多样性指标，数值越大表示多样性越高。在图10中，选取数据集pr152和lin318进行实验。从图中可以观察到，在pr152的实验中，两种算法的波动都相对稳定。然而，总体而言，LFACO的多样性要优于ACS。在lin318中，LFACO的波动范围较大，但总体上仍相对稳定，并且随着迭代次数的增加而缓慢上升。相比之下，ACS在算法迭代的早期保持了较好的多样性，但是不够稳定，并且随着迭代次数的增加，多样性逐渐下降。综上所述，LFACO在多样性方面表现更好。

3.4.2 与最新改进的蚁群算法对比

表5列出了LFACO与其他最新改进的蚁群算法的比较实验结果，包括HAACO［26］和GSACO［27］。HAACO是一种自适应的异构蚁群优化算法，结合了信息素适应策略、异构蚁群结构和3-opt局部搜索策略，用于解决旅行商问题。GSACO是一种使用自适应贪婪策略的蚁群优化算法。表中显示了七种不同规模的TSP实例的实验结果，可以看出，LFACO的数据均优于GSACO和HAACO。

4 结束语

在旅行商问题背景下，本文提出了一种基于MMAS的改进算法，该算法采用了莱维飞行策略和动态权重的混合转移规则。通过动态调整权重因子，使得算法在不同阶段能够灵活地选择三种转移规则的组合，从而提高了算法的收敛性能和解的质量。此外，算法还采用了随机多路径优化的3-opt策略和随机信息素重置策略，进一步提升了性能。研究阶段包括理论分析和实验验证。实验在MATLAB环境中使用多个TSP实例进行，首先，确定了合适的算法参数，包括混合转移规则的权重因子，通过单独的实验验证进行确定。然后，在TSP数据集上进行实验，并与传统的蚁群算法以及其他最新改进的蚁群算法进行对比。实验结果表明，LFACO在解的质量、收敛速度和避免陷入局部最优方面都具有显著优势。然而，本文算法在处理大规模TSP实例时仍有改进的空间。未来的研究将继续优化算法性能，并将其扩展到更复杂的组合优化问题，如车辆路径规划。

参考文献：

［1］Liu Meijiao，Li Yanhui，Li Ang，et al. A slime mold-ant colony fusion algorithm for solving traveling salesman problem ［J］. IEEE Access，2020，8： 202508-202521.

［2］Halim A H，Ismail I. Combinatorial optimization： comparison of heuristic algorithms in travelling salesman problem ［J］. Archives of Computational Methods in Engineering，2019，26： 367-380.

［3］陈加俊，谭代伦. 求解旅行商问题的探索-开发-跳跃策略单亲遗传算法 ［J］. 计算机应用研究，2023，40（5）： 1375-1380. （Chen Jiajun，Tan Dailun. Partheno-genetic algorithm based on explore-develop-jump strategy for solving traveling salesman problem ［J］. Application Research of Computers，2023，40（5）： 1375-1380.）

［4］禹博文，游晓明，刘升. 引入动态分化和邻域诱导机制的双蚁群优化算法 ［J］. 计算机应用研究，2023，40（10）： 3000-3006. （Yu Bowen，You Xiaoming，Liu Sheng. Dual-ant colony optimization algorithm with dynamic differentiation and neighborhood induction mechanism ［J］. Application Research of Computers，2023，40（10）： 3000-3006.）

［5］Zhang Panli，Wang Jiquan，Tian Zhanwei，et al. A genetic algorithm with jumping gene and heuristic operators for traveling salesman problem ［J］. Applied Soft Computing，2022，127： 109339.

［6］Roy A，Manna A，Maity S. A novel memetic genetic algorithm for solving traveling salesman problem based on multi-parent crossover technique ［J］. Decision Making： Applications in Management and Engineering，2019，2（2）： 100-111.

［7］lhan ，Gkmen G. A list-based simulated annealing algorithm with crossover operator for the traveling salesman problem ［J］. Neural Computing and Applications，2022，34： 7627-7652.

［8］Gharehchopogh F S，Abdollahzadeh B. An efficient Harris hawk optimization algorithm for solving the travelling salesman problem ［J］. Cluster Computing，2022，25（3）： 1981-2005.

［9］Zhang Jin，Li Hong，Liu Qing. An improved whale optimization algorithm for the traveling salesman problem ［J］. Symmetry，2020，13（1）： 48.

［10］Khan I，Maiti M K. A swap sequence based artificial bee colony algorithm for traveling salesman problem ［J］. Swarm and Evolutionary Computation，2019，44： 428-438.

［11］Xue Jiankai，Shen Bo. A novel swarm intelligence optimization approach： sparrow search algorithm ［J］. Systems Science & Control Engineering，2020，8（1）： 22-34.

［12］Zhang Zhen，Han Yang. Discrete sparrow search algorithm for symmetric traveling salesman problem ［J］. Applied Soft Computing，2022，118： 108469.

［13］Stützle T，Hoos H H. MAX-MIN ant system ［J］. Future Generation Computer Systems，2000，16（8）： 889-914.

［14］Colorni A，Dorigo M，Maniezzo V. Distributed optimization by ant co-lonies ［C］// Proc of the 1st European Conference on Artificial Life. 1991： 134-142.

［15］Lee Z J. A hybrid algorithm applied to travelling salesman problem ［C］// Proc of IEEE International Conference on Networking，Sensing and Control.Piscataway，NJ： IEEE Press，2004： 237-242.

［16］Cheng J，Zhang Gexiang，Li Zhidan，et al. Multi-objective ant colony optimization based on decomposition for bi-objective traveling salesman problems ［J］. Soft Computing，2012，16： 597-614.

［17］Ban Habang. The hybridization of ACO+GA and RVNS algorithm for solving the time-dependent traveling salesman problem ［J］. Evolutionary Intelligence，2022，15（1）： 309-328.

［18］Dahan F，El Hindi K，Mathkour H，et al. Dynamic flying ant colony optimization （DFACO） for solving the traveling salesman problem ［J］. Sensors，2019，19（8）： 1837.

［19］Yang Kang，You Xiaoming，Liu Shen，et al. A novel ant colony optimization based on game for traveling salesman problem ［J］. Applied Intelligence，2020，50： 4529-4542.

［20］Dorigo M，Stützle T. Ant colony optimization： overview and recent advances ［M］. Berlin： Springer International Publishing，2019.

［21］Dorigo M，Gambardella L M. Ant colony system： a cooperative lear-ning approach to the traveling salesman problem ［J］. IEEE Trans on Evolutionary Computation，1997，1（1）： 53-66.

［22］Zhong Changting，Li Gang，Meng Zeng. Beluga whale optimization： a novel nature-inspired metaheuristic algorithm ［J］. Knowledge-Based Systems，2022，251： 109215.

［23］Bansal S R，Goel R K，Maini R. An improved ant colony algorithm based on Lévy flight distribution ［J］. Advances in Mathematics： Scientific Journal，2020，9（6）： 3907-3916.

［24］Liu Yahui，Cao Buyang. A novel ant colony optimization algorithm with Lévy flight ［J］. IEEE Access，2020，8： 67205-67213.

［25］Liu Yahui，Cao Buyang，Li Hehua. Improving ant colony optimization algorithm with epsilon greedy and Lévy flight ［J］. Complex & Intelligent Systems，2021，7： 1711-1722.

［26］Tuani A F，Keedwell E，Collett M. Heterogenous adaptive ant colony optimization with 3-opt local search for the travelling salesman problem ［J］. Applied Soft Computing，2020，97： 106720.

［27］Li Wei，Xia Le，Huang Ying，et al. An ant colony optimization algorithm with adaptive greedy strategy to optimize path problems ［J］. Journal of Ambient Intelligence and Humanized Computing，2022，13： 1557-1571.