基于高频车站及时间窗的立体轨道交通系统智能调度算法

张帅 古玉锋 凌浩 黎程山

摘 要：立體轨道交通系统的车辆调度方法还未见报道，已有车辆调度算法的实时性较差。针对立体轨道交通车辆的调度问题，研究了一种结合高、低频车站判定的订单分配算法和一种结合时间窗的Dijkstra路径规划算法，即智能调度算法，以提高车辆的运行效率。首先，使用订单分配算法为订单选择合适的执行车辆，减少乘客的等待时间。其次，在订单分配算法的基础上增加了高、低频车站的判定，提前给高频车站调度车辆，以保证供需平衡。然后，将普通Dijkstra算法和时间窗判断相结合，以实现多车辆的无冲突路径规划。最后，对OpenTCS软件进行二次开发，并进行了调度算法的仿真。结果表明，当有乘客叫车时，若只有订单分配算法，乘客平均等待时间为8.043 s；结合高、低频车站进行车辆提前调度后，平均等待时间降到了5.724 s，每位乘客减少了2.319 s的等待时间。路径规划时，无论是普通的Dijkstra算法还是结合时间窗的Dijkstra算法，规划耗时都在1 ms以内，而结合时间窗的Dijkstra算法在只增加约0.1 ms耗时的情况下，解决了车辆的路径冲突问题。研究的智能调度算法减少了乘客的等待时间，提高了车辆的运行效率，实时性好，能满足立体轨道交通车辆的调度要求。

关键词：立体轨道交通； 智能调度； 高频车站； 订单分配算法； 时间窗； Dijkstra算法

中图分类号：U292.4 文献标志码：A 文章编号：1001-3695（2024）05-009-1343-06

doi：10.19734/j.issn.1001-3695.2023.09.0427

Intelligent scheduling algorithm of three-dimensional rail transit system

based on high-frequency station and time window

Abstract：At present， there are almost no reports on vehicle scheduling methods for three-dimensional rail transit system， and the real-time performance of existing vehicle scheduling algorithms is poor. Aiming at the scheduling problem of three-dimensional rail transit vehicles， this paper studied an order allocation algorithm combining high and low frequency station judgment and a Dijkstra path planning algorithm combining time window， namely intelligent scheduling algorithms， to improve the operating efficiency of vehicles. Firstly， it used the order allocation algorithm to select the appropriate execution vehicle for the order to reduce the waiting time of passengers. Secondly， it added the judgment of high and low frequency stations on the basis of the order allocation algorithm， and scheduled vehicles to the high frequency stations in advance to ensure the balance of supply and demand. Then， it combined the ordinary Dijkstra algorithm and time window judgment to realize multi-vehicle conflict-free path planning. Finally， it redeveloped the OpenTCS software and simulated the scheduling algorithm with the software. The results show that the average waiting time of the passenger from calling the vehicles is 8.043 s only using the order allocation algorithm. After the advance scheduling of vehicles combined with high and low frequency stations， the average waiting time is reduced to 5.724 s， and the waiting time of each passenger is reduced by 2.319 s. During the path planning， both the ordinary Dijkstra algorithm and the Dijkstra algorithm combined with time window took less than 1 ms to plan. However， the Dijkstra algorithm combined with time window only increases the time about 0.1 ms， and solves the problems of the vehicle path conflicts. The studied intelligent scheduling algorithm can reduce the waiting time of the passengers and improve the running efficiency of vehicles. The algorithm has good real-time performance and can meet the scheduling requirements of three-dimensional rail transit vehicles.

Key words：three-dimensional rail transit; intelligent scheduling; high frequency station; order allocation algorithm; time window; Dijkstra algorithm

0 引言

目前，交通拥堵已是城市普遍存在的问题。为了缓解交通压力，轨道交通里程越来越大，如何更科学合理地调度车辆、提高运营效率、提升乘车体验，是当前亟待解决的问题［1，2］。智能调度系统可以实时地对每辆自动驾驶车辆进行调度，并根据运行任务规划最优路线，可以极大地降低运营成本，减少乘客的等待时间，提高服务质量。其中，调度算法是智能调度系统的核心。

调度算法需要考虑车辆避障、算法运行效率、公司运营成本和车辆能源补给等问题［3，4］，广泛地应用于军事、物流及公共交通领域。文献［5］基于克隆选择算法，考虑公交车运行的时间表，提出了一种公交车调度方法，该算法得到调度解的时间较长，实时性略差。文献［6］采用竞拍算法，通过运输任务与车辆间的双向选择，对自动引导车（automated guided vehicle，AGV）进行调度，该算法没有考虑车辆不同速度的情况。文献［7］为解决公交车的资源分配问题，将遗传算法与禁忌搜索算法相结合，提高了求解性能，但不适用于实时调度。文献［8］针对舰载机在机库中的调度问题，采用凸壳算法获取可行路径，Dijkstra算法进行路径规划，算法没有考虑多架飞机同时调度时可能引发的路径冲突。文献［9］为了提高乘客叫车请求的响应速度，将遗传算法和贪婪算法结合，优先处理较早的叫车请求，但车辆的运行路径较为单一，没有针对各订单分别进行规划路径。文献［10］针对兵场站物资配送车辆的调度问题，在遗传算法的基础上增加了模拟退火算法，减少了陷入局部最优解的情况发生，但算法的运行时间较长，实时性差。文献［11］使用混合粒子群算法对轨道门吊的调度任务进行求解，减少了空驶行程，但算法求解时间在13 s以上，时间较长。文献［12］在轨道交通的调度问题上采用蚁群算法进行负载均衡调度，系统具有较高的任务吞吐量，但当任务量较小时，完成时间较长。

由已有文献可知，当前对于平面交通系统的车辆调度问题，已经取得了一定的研究成果。其中，遗传算法、模拟退火算法等启发式算法由于收敛速度较慢，不能满足立体轨道交通智能调度系统的实时性要求；Dijkstra算法用于解决正权值的单源最短路径问题是十分有效的［13， 14］，且求解速度快、实时性好。对于立体轨道交通，还需要考虑多车辆之间的路径冲突问题，通过判断各路段的时间窗是否存在重叠并作出相应动作，可以提前规避该问题发生。为此，本文将提前调度与订单分配算法结合，以减少车辆调度的等待时间，同时在Dijkstra算法中增加时间窗，以避免路径冲突，最终实现车辆的智能调度。

1 建立数学模型

1.1 问题描述

车辆调度要求有较高的实时性，即在调度系统收到调度请求后，在尽可能短的时间内响应请求，并按照调度规则，合理地规划车辆和路径，将车辆调度到指定地点。

本文智能调度算法的运行场景为一栋楼宇里的立体轨道交通，楼内竖移电梯与平移轨道车辆无缝连接，并实现自动驾驶，共同组成立体轨道交通系统。居民可以通过叫车软件设定目的地，由智能调度系统规划路线，点对点接送。其特征如下：

a）楼宇共五层，每50 m有一个车站，每个车站初始状态下有两辆车。

b）楼内各层之间有垂直方向运行的电梯，通过垂直轨道将车辆送入平移轨道。

c）车辆平移轨道位于第四层，有正向和反向两组轨道，各自单向行驶，每组分为低速、中速和高速三条轨道。

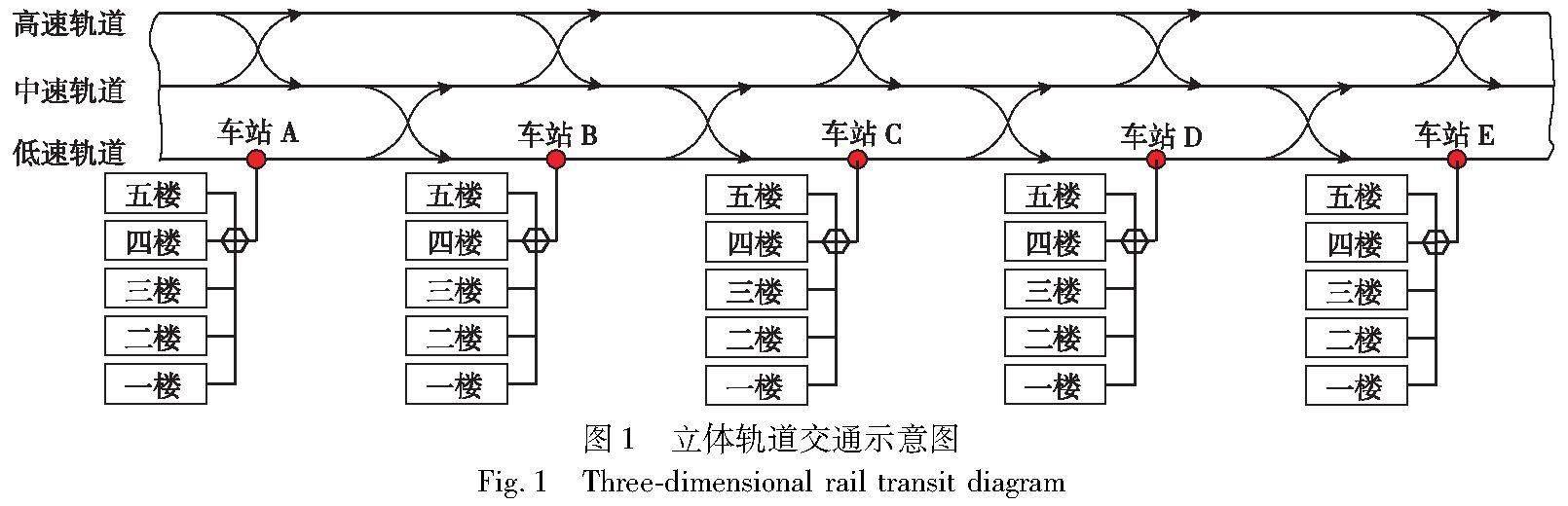
d）第四层中，每两个车站中间设有一个低-中速变道装置，每个车站处设有一个中-高速变道装置，车辆可通过变道装置双向变道。具体场景如图1所示。

1.2 模型假设条件

在智能调度系统中，公交车有三种状态：第一种是空闲状态，车辆停泊在车站里等待乘客下订单或等待调度系统的调度命令；第二种是空载状态，当调度系统发出指令将空闲车辆调度到订单起点时，便会空载运行；第三种是载客状态，就是执行订单任务将乘客从起点运送到目的地的过程。由于乘客所在车站和空闲车辆所在车站均具有随机性，使得乘客等车的时间长短具有不确定性，智能调度系统可以使每位乘客具有最优的等待时间。因此调度目标是为每位乘客选择最合适的车辆，尽可能减少车辆的空行程，缩短乘客的等车时间，使每位乘客尽可能早地开始行程，最终规划出耗时最短的车辆行驶路线。

在调度系统中，存在很多干扰调度结果的变量与影响因素，为了能更好地将其抽象为数学模型，本文从车辆的实际运营情况出发，作出以下假设：

a）所有车辆统一由智能调度系统进行指挥调度，车辆均为同一型号，不考虑发生故障的情况。

b）一辆车在同一时间只能处理一个订单，一个订单也只能由一辆车接收并处理，不考虑不同订单共享车辆的情况。

c）乘客数量不影响车辆的运行速度。

d）由于乘客上下车的时间为每次接驳的共有因素，对智能调度系统的决策不产生影响，故在本文模型中不考虑该因素。

e）不考虑乘客未能及时到达车站的情况，即不考虑车辆等待乘客的情况。

1.3 数学模型

理时间，rvi表示处理该订单的车辆。因为每位叫车的乘客仅对应一个叫车请求，所以完全可以用叫车请求代表乘客，下文将不再单独考虑乘客个体。

在智能调度系统中，为了最大程度地改善乘车体验，提高车辆的运行效率，需要将调度问题分为两部分考虑。首先是订单分配，即收到订单后将订单分配给合適的车辆，可以是空闲车辆，也可以是即将到站的运行车辆。分配给运行中的车辆时，需要先等待车辆完成当前订单，再将其调度到叫车地点。对此提出第一个优化目标：某一时刻提交的所有订单中，乘客的平均等待时间尽可能短；其次是车辆运行路径的规划，通过变道系统适时地在低速、中速及高速车道之间切换，规划出耗时最短的路线。对此提出第二个优化目标：某一时刻提交的所有订单总处理时间尽可能短。根据以上内容，列出目标函数如下：

目标函数1：

目标函数2：

其中：Thandle为t时刻所有订单总处理时间；tstarti为乘客上车时间，即车辆出发时间；tendi为车辆到达目的地的时间。

目标函数1表示在某一时刻提交的所有订单中乘客的平均等待时间；目标函数2表示某一时刻提交的所有订单的总处理时间。为达到上文中的两个优化目标，需使式（1）和（3）的值尽可能小。下文将结合订单分配算法和路径规划算法对目标进行优化。

2 智能调度算法研究

2.1 订单分配算法

订单分配算法的主要目标是优化乘客的等车时间，提高交通系统的运行效率。订单分配算法的着重点在于为每一个订单选择合适的车辆，当车辆接收到订单任务后，只需按订单指示的站点运行即可。本节将以目标函数1为优化目标设计订单分配算法。

运用上述订单分配算法，可以选出合适的车辆，使乘客等车时间尽可能短，从而提高系统的运行效率。然而，在实际运营场景中，各个车站的人流量以及订单数量存在较大差异，由此出现了一些高频车站和低频车站。为此，本文提出一种提前调度的方法，对调度系统进行进一步优化。

提前调度是指在系统收到订单之前就开始进行车辆的调度工作，向高频车站派遣更多车辆。当一个车站被判定为高频车站时，调度系统会提前将低频车站的部分空闲车辆调度到该车站，以保证供需平衡，尽可能避免接收到订单后由于起始站空闲车辆不足而需要从其他车站调度车辆的情况，从而缩短乘客不必要的等车时间。据此提出的高、低频车站的判定公式如式（5）（6）所示。

NR（T）表示0～T时间段内的订单数量。

设高频车站的频率阈值为Phigh，低频车站的频率阈值为Plow。如果Psi（T）>Phigh，则认为车站si在该时间段内为高频车站；如果Psi（T）

2.2 结合时间窗的路径规划算法

上文解决了订单分配的相关问题，下一个问题是已知车辆起始站和终点站的情况下的路径规划问题。本节将以目标函数2为优化目标，设计车辆的路径规划算法。

Dijkstra算法是一种具有代表性的单源最短路径算法，结合了贪心思想和松弛操作，从起始点开始逐层向外扩展，直到找出其他所有节点的最短路径。由于车辆是在轨道上行驶的，并不能通过变换位置来给其他车辆让行，所以在多车辆的环境中，如果分别对各个车辆进行路径规划，必然会出现路径冲突的情况。本文的路径冲突主要表现为两种变道冲突，一种是变道车辆与已在目标车道上运行的车辆产生的冲突，如图3所示；另一种是交叉变道时产生的冲突，如图4所示。对此需要引入时间窗的概念，将其与Dijkstra算法相结合，达到所有车辆均能正常运行的目的。

时间窗主要是指某一路段被某一车辆所占用的时间段，设Windowspvi=［tstartvi，p，tendvi，p］表示车辆vi通过路段p所占用的时间窗，tstartvi，p表示时间窗的开始时间，tendvi，p表示时间窗的结束时间。使用Dijkstra算法规划路径时，系统会给车辆途径的每个路段分配时间窗，通过避免时间冲突来保证各车辆的正常运行。基于该思想，列出以下不等式：

式（7）表示在车辆vi离开路段p时，车辆vj还未到达该路段。式（8）表示在车辆vi到达路段p时，车辆vj已经离开该路段。当路径中的所有路段均满足以上两个公式时，即可避免车辆发生碰撞，若某个路段不满足条件，则增大该路段的权值并重新使用Dijkstra算法规划路径。

在高频车站附近的路段和变道装置时间窗非常密集，这将导致系统频繁重新规划路径，造成资源浪费。为提高系统效率，在使用式（5）（6）确认出高频车站以后，将进出这些站点必经的路段以及变道装置的权值适当提高，在首次规划路径时就尽可能地避开这些车流量大的路段，减少重新规划路径的次数。图5为当车站C三楼被列为高频站点时，提高权值的路段示意图。改进后的路径规划算法具体流程如下：

a）访问订单列表，查询并统计所有订单的起始站和终点站。

b）通过式（5）（6）计算各站点出现的频率，然后判断并记录下高频车站。

c）提高进出高频站点必经路段和变道装置的权值。

d）获取当前订单中（或调度任务中）的起始站和终点站。

e）使用Dijkstra算法找出最短路径。

f）为途径的每个路段分配时间窗。

g）遍历每个时间窗，分别使用式（7）（8）进行判断。

h）若每个时间窗都满足式（7）或（8），則跳转至步骤j），否则进入步骤i）。

i）提高不符合条件的路段权值，然后跳转至步骤e）。

j）完成路径规划。

路径规划算法的流程如图6所示。

3 算法的仿真与结果分析

3.1 建立地图模型

OpenTCS软件是一款开源的有轨自动小车可视化仿真软件，本文使用该软件建立地图模型，并在此软件框架的基础上进行二次开发，以测试本文所研究的订单分配算法和路径规划算法。在OpenTCS软件上建立的地图模型如图7所示，模型由三条轨道和55个站点组成，轨道上总共有11个车站，每个车站都有5个站点可以选择，分别对应五个楼层。三条轨道从上到下分别对应低速、中速、高速轨道。

3.2 仿真结果与分析

首先是订单分配，本文先在某一路段内随机生成一组车辆位置，有的正在轨道上运行，有的在车站里处于空闲状态。然后又随机生成十个叫车地点，分别用本文研究的订单分配算法给车辆分配订单，记录车辆收到订单后调度到叫车地点的用时。实验数据如表1和2所示，其中V（vehicle）代表车辆，P（point）代表点，L（location）代表车站位置，实验结果如图8所示。当某车站有乘客提交订单时，无论是将订单分配给运行中的车辆，还是分配给空闲车辆，都会存在比另一方等待时间更长的情况，而通过订单分配算法，可以使乘客的等待时间达到最短。

在表2中，十个叫车地点中L-038和L-050两个车站均出现了两次，将其设为高频车站，提前给这两个车站增派其他路段的空闲车辆后，乘客的等待时间如图9所示。经计算，结合提前调度后，乘客平均等待时间由8.043 s降到了5.724 s，相当于每位乘客减少了2.319 s的等待时间。

在路径规划算法的仿真中，本文随机生成了十个订单，分别用结合时间窗的Dijkstra算法和普通Dijkstra算法进行了路径规划。由于普通Dijkstra算法规划的路径不考虑各车辆的路径冲突，规划出来的路线参考价值不大，所以本文只对其规划耗时进行对比分析。本次仿真所用到的订单如表3所示。结合时间窗的Dijkstra算法所规划出的部分路徑如图10所示。

图11为分别用结合时间窗的Dijkstra算法和普通Dijkstra算法对这十个订单进行路径规划的耗时，两者的规划耗时都在1 ms以内。通过表4对比可见，本文算法的平均执行时间远小于已有的启发式算法。结合时间窗的Dijkstra算法由于增加了时间窗判定流程，比普通Dijkstra算法用时略长，增加了约0.1 ms，但对于路径冲突来说，是非常有意义的。

图11中的4号订单规划用时为0.558 ms，显著长于其他订单规划用时，原因是首次路径规划时检测到了路径冲突，并且在提高冲突路段权值后重新进行了路径规划。如图12所示，红色路径为n号订单规划好的路径，在m号订单规划路径时，初次规划的路径与n号订单相同，但由于检测到了两者之间存在时间窗冲突，系统便提高了冲突路段的权值，重新规划的路径如图12中蓝色路径所示。与原路径相比，相当于车辆通过提前变道避免了这次路径冲突。

4 结束语

本文针对立体轨道交通系统的调度问题，将算法分为订单分配算法和路径规划算法两部分进行考虑。研究了一种立体轨道交通车辆的订单分配算法，根据乘客的叫车地点，选择调度时间最短的车辆进行订单分配，减少了乘客的等待时间。在该算法的基础上增加了高、低频车站的判定，提前给高频车站调度空闲车辆，进一步减少了乘客的等待时间。针对多车辆情况下普通Dijkstra算法规划路径时不考虑路径冲突的问题，研究了一种结合时间窗的Dijkstra算法，通过时间窗判断是否存在路径冲突，若存在冲突则提高相应路段的权值，并重新使用Dijkstra算法规划路径，保证所有车辆都能正常运行。

结合本文算法对OpenTCS软件进行了二次开发，并进行仿真测试。测试结果表明，当乘客发起叫车请求时，在订单分配算法的基础上增加提前调度后，有效地将乘客的平均等待时间由8.043 s降到了5.724 s，减少了2.319 s。其次，路径规划时，结合时间窗的Dijkstra算法和普通Dijkstra算法的规划耗时都在1 ms以内，而结合时间窗的Dijkstra算法在只增加约0.1 ms耗时的情况下，实现了无冲突的路径规划，使所有车辆均可正常运行。本文研究的调度算法和已有算法相比，有实时性高、规划耗时短等优点，可以满足立体轨道交通系统的调度要求。算法的下一步研究将引入车站间距、变道装置的数量等因素，对算法作进一步优化。

参考文献：

［1］张思维， 魏昕怡， 邱桃荣. 优化公交车调度的多目标遗传算法模型［J］. 南昌大学学报： 理科版， 2022，46（1）： 60-65. （Zhang Siwei， Wei Xinyi， Qiu Taorong. Multi-objective genetic algorithm model for optimizing bus dispatch［J］. Journal of Nanchang University： Natural Science， 2022，46（1）： 60-65.）

［2］赵娜， 袁家斌， 徐晗. 智能交通系统综述［J］. 计算机科学， 2014，41（11）： 7-11，45. （Zhao Na， Yuan Jiabin， Xu Han. Survey on intelligent transportation system［J］. Computer Science， 2014，41（11）： 7-11，45.）

［3］Li Jingquan. Transit bus scheduling with limited energy［J］. Transportation Science， 2014，48（4）： 521-539.

［4］Tang Jiafu， Guan Jing， Yu Yang， et al. Beam search combined with MAX-MIN ant systems and benchmarking data tests for weighted vehicle routing problem［J］. IEEE Trans on Automation Science and Engineering， 2014，11（4）： 1097-1109.

［5］Shui Xinguo， Zuo Xingquan， Chen Cheng， et al. A clonal selection algorithm for urban bus vehicle scheduling［J］. Applied Soft Computing， 2015，36： 36-44.

［6］Lim J K， Kim K H， Yoshimoto K， et al. A dispatching method for automated guided vehicles by using a bidding concept［J］. OR Spectrum， 2003，25（1）： 25-44.

［7］Zhang Feizhou， Cao Xuejun， Yang Donggai. Intelligent scheduling of public traffic vehicles based on a hybrid genetic algorithm［J］. Tsinghua Science and Technology， 2008，13（5）： 625-631.

［8］司维超， 齐玉东， 韩维. 基于融合Dijkstra的凸壳算法的舰载机机库调运规划［J］. 系统工程与电子技术， 2015， 37（3）： 583-588. （Si Weichao， Qi Yudong， Han Wei. Carrier plane transportation in hangar based on convex hull algorithm combined with Dijkstra［J］. Systems Engineering and Electronics， 2015，37（3）： 583-588.）

［9］李爽， 杨明， 王春香， 等. 面向全自动控制交通系统的车辆调度算法［J］. 上海交通大学学报， 2017， 51（2）： 174-179. （Li Shuang， Yang Ming， Wang Chunxiang， et al. Scheduling algorithm for vehicles in cybernetic transportation system［J］. Journal of Shanghai Jiaotong University， 2017，51（2）： 174-179.）

［10］阎哲， 汪民乐， 汪江鹏， 等. 基于混合遗传算法的海军航空兵场站物资配送车辆调度智能优化［J］. 系统工程与电子技术， 2023，45（12）：3908-3914. （Yan Zhe， Wang Minle， Wang Jiangpeng， et al. Intelligent optimization of vehicle scheduling for material distribution in naval aviation station based on hybrid genetic algorithm［J］. Systems Engineering and Electronics， 2023，45（12）：3908-3914.

［11］王力， 朱晓宁， 闫伟， 等. 铁路集装箱中心站轨道门吊调度优化模型与算法［J］. 铁道学报， 2014，36（5）： 8-13. （Wang Li， Zhu Xiaoning， Yan Wei， et al. Optimization model and algorithm of rail mounted gantry crane scheduling at railway container terminals［J］. Journal of the China Railway Society， 2014，36（5）： 8-13.）

［12］堯海昌， 柴博周， 刘尚东， 等. 基于蚁群算法的轨道交通集群调度算法研究［J］. 南京邮电大学学报： 自然科学版， 2018， 38（4）： 81-88. （Yao Haichang， Chai Bozhou， Liu Shangdong， et al. Load balancing scheduling algorithm for rail transit cluster based on ant colony algorithm［J］. Journal of Nanjing University of Posts and Telecommunications： Natural Science Edition， 2018，38（4）： 81-88.）

［13］宋翠颖， 王鹤玲， 田泽尚， 等. 需求响应式公交车辆调度模型和算法研究综述［J］. 北京交通大学学报，2023，47（4）：31-44. （Song Cuiying， Wang Heling， Tian Zeshang， et al. Review of demand-responsive transit vehicle scheduling models and algorithms［J］. Journal of Beijing Jiaotong University， 2023，47（4）：31-44.）

［14］Akram M， Habib A， Alcantud J C R. An optimization study based on Dijkstra algorithm for a network with trapezoidal picture fuzzy numbers［J］. Neural Computing and Applications， 2021，33（4）： 1329-1342.