基于Rasch模型的理科生科学推理能力测评研究

程朝娟 朱巧萍

摘要：科学推理是科学思维的重要组成部分。基于Rasch模型运用LCTSR 2000对419名理科生的科学推理能力进行测评研究，分析量表的质量和被试科学推理能力发展情况。研究表明：理科生的科学推理能力各维度发展不均衡；科学推理能力与学业成绩呈较低的正相关；男生的科学推理能力略高于女生，科学推理能力不存在显著的性别差异。依据实证研究结果，对影响科学推理能力发展的主要原因进行讨论，并提出相应的教学建议。

关键词：Rasch模型；科学推理能力；质量分析；测评研究；教学建议

中图分类号：G633.7文献标志码：A文章编号：16735072（2024）03033508

皮亚杰认为科学推理是一种由认知发展进入形式操作阶段后，儿童或成人所具备的一种推理方式［1］。Zimmerman［2］认为科学推理是运用科学探究方法或者原则进行推理并解决问题的过程。Lawson［3］把科学推理能力分成6个维度，即质量与体积守恒推理、比例推理、概率推理、控制变量推理、假设演绎推理和相关推理。《普通高中物理课程标准（2017年版）》［4］和《义务教育物理课程标准（2022年版）》［5］认为科学思维是物理学科核心素养要素之一，而科学思维包含科学推理。所以，进行科学推理能力的测评分析，对物理教学中提升学生物理学科核心素养具有重大意义。

LCTSR 2000量表在教育研究中被广泛用来测量学生的科学推理能力发展情况。从研究对象来看，运用该量表可以研究从小学到本科的各个阶段学生的科学推理能力。从研究内容来看，就科学推理能力发展水平而言，魏昕等［6］研究了中小学生的科学推理能力随年级变化的发展规律，刘成英等［7］发现，从小学到大学的学生科学推理能力出现阶段性上升；在影响科学推理能力的因素方面，主要有宏观外部环境、学科知识、教学模式、性别、个体能力等因素。从研究方法来看，大多数科学推理测评研究是根据经典测量理论，极少是根据项目反应理论进行科学推理能力测评研究。

传统的经典测量理论具有测量依赖性和样本依赖性，无法避免题目难度估计和被试能力估计的相互干扰问题。项目反应理论能够克服经典测量理论的局限性，并具有测量客观性和等距性等优点。基于项目反应理论的Rasch模型能够平衡被试能力和题目难度之间的关系，保证测评的客观性和准确性。本研究选取刚从高中毕业进入大学阶段的大一新生进行测试，基于项目反应理论下的Rasch模型先对LCTSR 2000量表进行质量分析，再科学、客观地对高中阶段科学推理能力的培养情况进行探讨，并对影响科学推理能力发展的因素进行讨论，为中学物理教学提供教学建议，完善教学模式。

1测量分析

1.1研究对象对已经完成中学物理课程的理科生的科学推理能力进行测试，可以较好地反映高中生科学推理能力的培养情况。本研究以宁夏大学的物理学院和电子与电气工程学院的大一学生作为研究对象，专业为物理学、应用物理、电子信息工程、电气工程及自动化和新能源材料与器件。该测试采用纸笔测试，测试时间为30分钟，共发放测试卷456份，剔除无效答卷，得到有效答卷419份，其中男生307名，女生112名。

1.2測评工具LCTSR 2000量表共有24道题目，测试科学推理能力6个子维度的题目分布如表1。24道题目共描述了12个问题情境，每2道题目为一组。测试结果采用二级计分方式，测试卷的总分为24分，回答正确计1分，回答错误计0分。

1.3研究工具

项目反应理论认为，被试学生是否答对题目不仅取决于被试能力水平的高低，而且受题目难度等其他因素的影响。不同能力水平的学生在不同题目上的反应会有区别，从被试的反应能够估计被试的能力水平。使用概率函数预测被试正确回答的概率，被试的回答结果由被试能力与题目特性相互作用而产生［8］。

丹麦物理学家Georg Rasch于1960年提出基于项目反应理论的Rasch模型。Rasch模型为教育学、心理学提供了更为客观性的测量方法。Rasch模型是一种理想的模型，被试能力、题目难度以及被试正确作答的概率之间的关系可以用方程式（1）来表示。

式中：θm表示被试能力，δi表示题目难度，Pm表示答对概率［9］。个体能否正确回答题目，完全取决于个体能力和题目难度之间的比较。

Rasch模型具有以下优点［10］：（1）将原始分数转化为Logit得分，使得测量分数具有等距性；（2）被试能力分布与题目难度分布之间相互独立，互不影响；（3）被试能力和题目难度是根据被试在题目上的反应通过数学模型估算得到，使测量结果具有精确性；（4）将被试能力和题目难度放在同一量尺上，数据可进行比较。

1.4数据分析方法及过程

科学推理能力测评是通过被试作答24道题目的情况，来测量不可直接观察到的、潜在的物理量（即学生科学推理能力）。采用Winsteps软件进行Rasch分析，对量表的质量进行检验，包括题目信度、被试信度、分离度、怀特图、具体题目拟合度和气泡图等。根据怀特图判断被试能力与题目难度的分布情况，并对各维度进行归一化处理，判断科学推理各维度难度分布情况。运用Rasch模型对所有测试数据进行处理得到个体能力值（即Logit得分），对学生的科学推理能力进行描述性统计分析，并研究科学推理能力与高考课程成绩以及性别之间的相关性。

2科学推理量表质量分析检验

2.1整体质量检验

对419名被试的24个题目数据进行整体质量检验，结果如表2所示。

Rasch模型一般将题目难度均值设为0，被试能力平均值为0.33，与题目难度均值相差不大，说明题目整体能够与学生能力水平相匹配。Infit MNSQ是加权均方拟合统计量，Outfit MNSQ是未加权均方拟合统计量。MNSQ的理想值为1，在0.5～1.5表示数据与Rasch模型拟合较好。ZSTD统计量是拟合统计量，其理想值为0，当ZSTD值在-2～2时，说明拟合程度较好。由表2可知，被试能力和题目难度的拟合度指标均在可接受范围内，这意味着数据与Rasch模型拟合程度较好。

分离度反映被试能力与题目难度在研究变量上的分离程度，取值大于2时，区分度较好。被试能力的分离度为1.68，说明被试的能力分布比较窄；题目难度的分离度为9.05，表明题目能很好区分被试能力。

信度的理想值是1，如果测试的信度超过0.7，则表示测试的信度较高，如果测试的信度在0.6～0.7，则表示测试的信度良好。根据表2可知，被试信度为0.74，题目信度为0.99，信度较高，说明被试能力和题目难度的测验结果的可信度很高。

2.2被试能力与题目难度匹配度分析

如图1所示，Rasch模型将被试能力与题目难度以对数形式转换为等距的Logit区间，并通过怀特图表现出来。中间的竖线为Logit刻度尺，旁边的M为平均值，S代表一个标准偏差，T代表2个标准偏差。最左边的数字代表的是考生的能力水平与科学推理题目难度的Logit得分，从上到下，Logit值会减少，意味着考生的能力水平会下降，题目的难度也会降低。标尺的左边显示学生能力水平的数量分布，1个“#”代表3，一个“.”代表1或2。标尺右边是题目的难度分布情况，数字编号代表不同题目。

由图1可知，被试学生能力水平分布范围约为8个Logit区间，题目难度分布范围约为4个Logit区间。怀特图的理想分布情况是，不同难度的题目均有对应水平的被试，被试分布比较密集处所对应的题目数量应相对较多，高水平的学生应有高难度题目与之对应。本研究中，被试集中分布在中部，上下分布较少，说明被试能力大致呈正态分布。从分布对应的情况来看，缺乏高水平的题目与高水平的学生相对应，题目的难度分布没有很好地覆盖所有水平的学生。被试能力均值M与题目难度均值较接近，表明题目难度整体适当。

2.3具体题目拟合度与误差分析

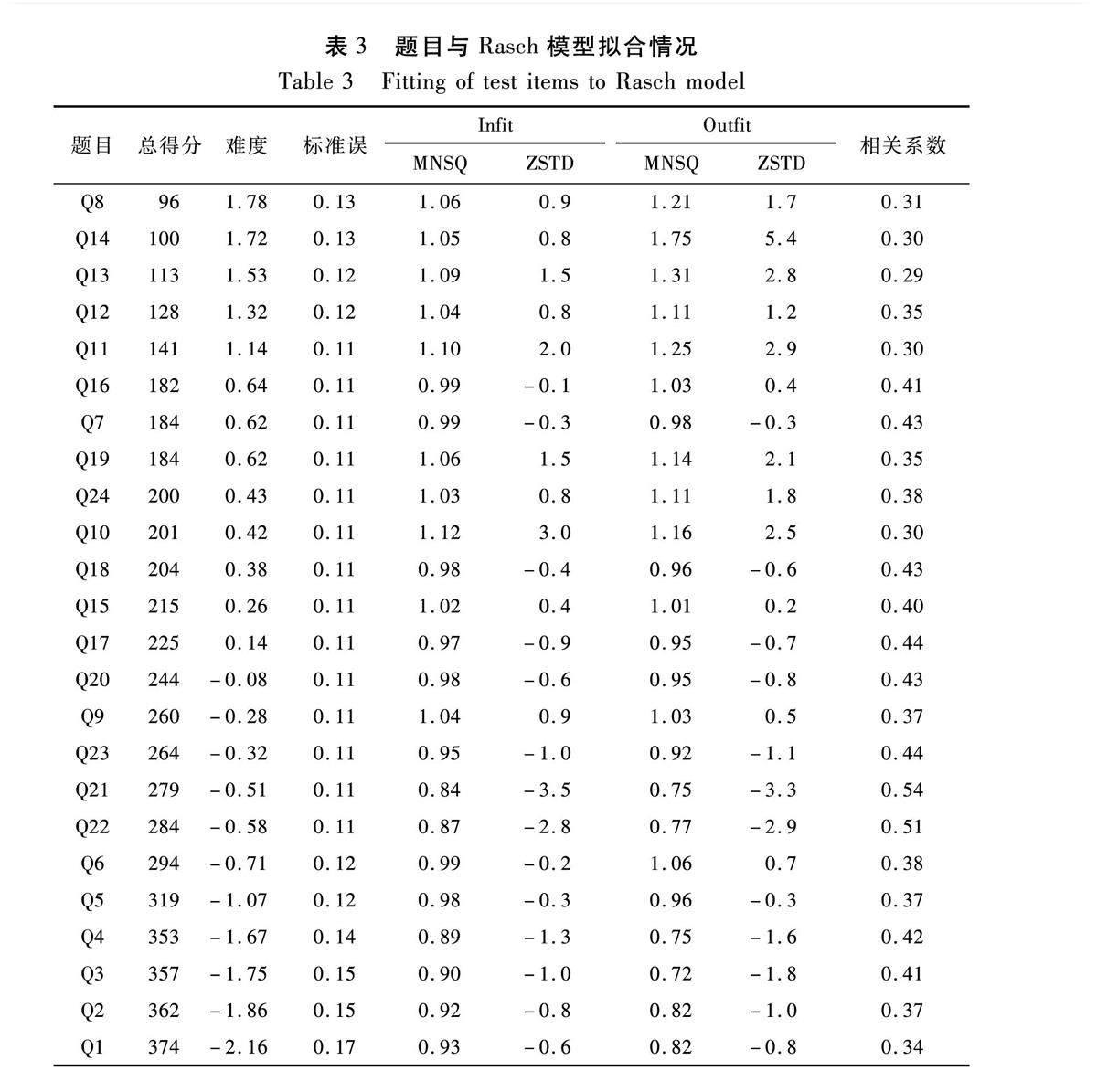
题目难度与Rasch模型的拟合情况如表3所示，从上往下题目难度依次降低。测量的误差用标准误表示，标准误越小，表明题目对学生的估计结果越稳定，题目的可信度越高。题目和测验目标之间的关联性可以用相关系数来表达，相关系数越大，说明题目与测验目标的关联性越高。

每道題目的标准误为0.11～0.17，都小于0.40，说明测试得到的题目难度值与真实值比较接近，数据可靠性较高。相关系数在0.29～0.54，与测量目标均正相关。第13题为0.29，其他题目都大于或等于0.30。说明第13题与测量目标正相关性不明显，该题在测评被试学生的科学推理能力水平时，获得的有效信息较少。

Infit MNSQ为0.84～1.12，均在理想范围内；Outfit MNSQ为0.72～1.75，除了第14题大于1.5外，其余所有题目均在0.50～150。表明该测验题目具有很好的拟合度和质量，可以对学生的科学推理能力进行正确的评价。

2.4气泡图

气泡图能够更加直观地反映题目的测量误差和拟合情况，如图2所示。每个气泡表示1个题目，气泡的大小代表的是标准误，气泡越小，则标准误越小，测量结果更加精确。部分题目气泡重叠在一起，说明这些题目的难度和拟合指标相接近。横坐标代表未加权均方拟合统计量，纵坐标代表题目难度值，从下往上题目难度依次增大。所以，第1题难度最小，第14和8题难度很大。除了第14题Oufit MNSQ不在理想范围内，其余题目的拟合度在可接受范围，这与具体题目分析拟合的结果是一样的。

3科学推理能力测评分析

3.1被试科学推理能力总体表现水平

被试总体科学推理能力描述性统计如表4所示。被试学生的科学推理能力的Logit得分全距为7.70，样本学生的科学推理能力水平差异较大、分布较广。能力均值为0.33，均值标准误为0.05，数据的可信度高。

3.2被试科学推理能力各维度表现情况

被试在各维度的人均能力得分见表5，将其进行归一化处理，即每个维度的人均得分除以该维度题目的总分值，从而比较被试的科学推理能力在各维度的表现情况。根据归一化结果绘制的雷达图如图3所示，被试科学推理能力的各个维度发展不均衡。对比图1和图3 可知，守恒推理维度题目对于被试而言较简单，被试得分较高；控制变量、概率、相关、比例推理维度题目对于被试较难，得分较低。可见，理科生的守恒推理能力发展较好，控制变量推理能力、概率推理能力、相关推理能力和比例推理能力发展较差。

3.3被试科学推理能力与高考成绩相关性

被试的能力值（Logit得分）与高考成绩的皮尔逊相关分析结果如表6所示，被试的科学推理能力与高考课程成绩存在正相关，说明课程成绩较好的学生，科学推理能力水平也较高。但相关系数均小于0.5，说明相关程度较低。

3.4不同性别学生科学推理能力对比分析

不同性别学生科学推理能力的描述性统计如表7所示。男生的科学推理能力均值为0.368，女生为0

227，男生的科学推理能力略高于女生。将男生和女生的科学推理能力Logit得分进行独立样本t检验。结果表明，双尾显著性是0.223，大于0.05，说明被试科学推理能力无显著的性别差异。

4讨论

4.1学科知识与科学推理能力的关联性Bao等［11］通过对比研究得出，中美大学生的学科知识能力存在显著差异，而科学推理能力差异并不显著，表明科学推理能力受物理知识的影响很小。李力舟等［12］研究显示，高一学生的科学推理能力水平与其所掌握的物理知识有密切的关系。皮亚杰等［13］认为，儿童的7—10岁是具体运算阶段，11—15岁是形式运算阶段。个人的认知阶段会对科学推理能力产生很大的影响，每一个认知阶段都有一个特殊的窗口期［14］。高一学生是在形式运算阶段，物理知识对高一学生的科学推理能力有一定的促进作用。从高中毕业进入本科阶段的学生的科学推理能力已经达到稳定状态，可能不会随着学科知识而发生变化，此阶段学科知识与科学推理能力不具有显著性相关。所以，不同阶段的学生，物理学科知识对科学推理能力的影响可能会有所区别。

4.2教学模式对科学推理能力的影响

中学物理教学模式对学生科学推理能力会产生比较大的影响。探究式教学能够有效提升学生的学科知识水平以及科学推理能力［15］。接受过探究式教学的学生相比于接受传统教学的学生，在控制变量推理和相关推理能力等方面发展较好［16］。目前中学物理教学以传统传授式教学为主，直接传授物理概念、规律给学生，通过大量的习题来巩固物理知识，忽略了对学生思维能力的培养。守恒推理题目主要考察质量和体积等基础概念，通过中学阶段的物理教育传统教学模式，学生能够具备基本的守恒推理的思维能力。相关推理是科学探究式教学所涉及的推理能力，是在确定变量之间的相互关系的一种思维形式。控制变量推理需要让学生经历科学探究过程，通过科学地控制变量，对假设进行检验。理科生在控制变量推理和相关推理方面较弱，可能与采用传统教学模式有关。所以，采取探究式教学模式有利于提升学生的科学推理能力。

当学生经过模型建构，需要使用适当的数学分析方法进行推理，并得到正确的结论，学生的科学推理能力才能得以提高［17］。概率推理是由已知的变量信息来推导未知变量信息的过程，概率推理往往会需要结合数学运算。比例推理要求通过已知信息和比例的相关性质，并能够根据具体的情境把握数量关系的变化，从而进行数学运算及推理的过程。学生运用比值定义法来构建科学概念时，需要有较大的数学运算。概率推理和比例推理能力维度题目对于理科生而言较难，可能与中学物理教学中教师对于复杂的物理情境蕴含的数学问题没有深入剖析有关。

4.3科学推理能力的性别差异Linn［18］和Burbules［19］研究得出，在高中阶段，男生的科学推理能力通常优于女生。男生的思维往往更加倾向于抽象思维，擅长分析与推理，思维的灵活性较好；女生更加偏向于形象思维，善于模仿，关注细节［20］，能把握问题的整体与部分之间的联系，擅长类比以及联想，推理分析能力较薄弱。冯秀梅等［21］研究表明中美大学生的科学推理能力整体存在性别差异，其中，美国学生的性别差异较显著，而中国学生的性别差异相对较小。李梦宇等［22］研究得出高二学生的科學推理能力存在显著的性别差异。李力舟等［12］研究得出可能女生更适应传统的物理教学模式。

本研究得出科学推理能力不存在显著的性别差异，女生可能更适应当下的物理教学模式，所以会缩短与男生之间的科学推理能力差异，从而使得科学推理能力不存在显著的性别差异。对于不同的被试，科学推理能力的性别差异研究可能会有不一样的结果，科学推理能力与性别之间的关系还有待继续考究。

5建议

5.1均衡发展各维度科学推理能力

优化物理课程设置，重视物理实验探究课程。教师需要引导学生进行探究性实验，在实验探究环节，创设物理情境，设置有梯度的物理问题；引导学生使用归纳、推理和论证等科学思维方法解决相关物理实验现象及数据；在探究过程中重视培养学生的控制变量推理能力以及相关推理能力，使学生的思维呈阶梯式发展，提升学生物理学科核心素养。

注重运用数学方法解决复杂物理情境问题。学生在复杂的物理情境中运用数学方法解决问题，仍然需要合适的引导和训练。物理教学中教师要引导学生发散数理思维，引导学生将复杂物理问题转化成数学问题或者运用数学方法解决物理问题，培养学生能够根据物理情境运用数学分析方法进行科学推理的能力，同时注重提升学生的概率推理能力以及比例推理能力。

5.2物理教学中注重培养学生科学推理能力

理科生的科学推理能力与课程成绩呈较低的正相关，因此，对于中学物理教学如何提升学生的科学推理能力还需要多加思考。“新高考”教育改革背景下，应该减弱“应试教育”和“题海战术”的影响，发挥学生的主体性以及能动性，重视过程性学习，提升学生综合素质能力。创设真实情境，引导学生提出问题，在解决问题过程中提炼出相关物理概念、物理规律，并进行判断、推理，最后得出结论，在此过程中不断发散思维，促进科学推理能力的提升。

5.3正确看待科学推理能力性别差异

在教学过程中，需要消除“女生适合学文科，男生适合学理科”的刻板观念。尊重个体发展的特点及能力水平，针对性采取不同的教学策略和方法，因材施教，给予每一位学生自信心，鼓励学生从多角度思考问题，培养推理论证的习惯，提升学生的科学推理能力。

5.4高校应注重学生的科学推理能力培养

在大学教育中，应注重提升大学生的科学推理能力。首先，合理安排基础性与实践性教学的比例，注重实验教学和小组讨论等教学方法，引导学生进行科学推理，促进理科生的科学推理能力的发展。其次，要充实实践性教学资源，营造科研活动氛围，增强学生的实际操作能力，并将其与大学生的创新创业活动有机地结合起来，以培养学生的创造能力和实践能力。同时，大学生也应主动摄取知识，善于思考，积极参与创新实践活动，对研究问题进行深度挖掘，进行科学推理，质疑创新，不断提升自身的科学推理能力。

参考文献：

［1］严文法，胡卫平.国外青少年科学推理能力研究综述［J］.外国中小学教育，2009（5）：2328.

［2］ZIMMERMAN C.The development of scientific thinking skills in elementary and middle school［J］.Developmental Review，2006，27（2）：172223.

［3］LAWSON A E.The development and validation of a classroom test of formal reasoning［J］.Journal of Research in Science Teaching，1978，15（1）：1124.

［4］中华人民共和国教育部.普通高中物理课程标准（2017年版）［S］.北京：人民教育出版社，2020.

［5］中華人民共和国教育部.义务教育物理课程标准（2022年版）［S］.北京：人民教育出版社，2022.

［6］魏昕，郭玉英，徐燕.中小学生科学推理能力发展现状研究：以北京市中小学生为样本［J］.北京师范大学学报（自然科学版），2011，47（5）：461464.

［7］刘成英，李太华，刘忠旭，等.学生科学推理能力发展规律与阶段特征：基于1887名学生的测量分析［J］.上海教育科研，2019（7）：2529.

［8］王玥，常淑娟，韩晓玲，等.基于项目反应理论的题库构建及其有效性检验：以“现代教育技术”公共课为例［J］.现代教育技术，2019，29（10）：4147.

［9］晏子.心理科学领域内的客观测量：Rasch模型之特点及发展趋势［J］.心理科学进展，2010，18（8）：12981305.

［10］韦斯林，柳秀峰，王祖浩.基于Rasch理论的计算机模型教学测验的设计与应用［J］.中国电化教育，2014（7）：139144.

［11］BAO L，CAI T F，KOENIG K，et al.Physics.Learning and scientific reasoning.［J］.Science，2009，323（1）：586587.

［12］李力舟，魏昕，郭玉英.民族地区中学生科学推理能力的研究［J］.内蒙古师范大学学报（教育科学版），2013，26（12）：129132.

［13］皮亚杰.发生认识论原理［M］.王宪钿，译.北京：商务印书馆，1981.

［14］古德.罗纳德.G.儿童如何学科学：概念的形成和对教学的建议［M］.张东海，译.北京：人民教育出版社，2005.

［15］LAWSON A E，ALKHOURY S，BENFORD R，et al.What kinds of scientific concepts exist？ Concept construction and intellectual development in college biology［J］.Journal of Research in Science Teaching，2000，37（9）：9961018.

［16］王萌萌，赵敏，方恺.探究式教学模式对本科生科学推理能力培养的效果分析［J］.物理与工程，2018，28（5）：110113.

［17］吴春晓，黄致新.如何培养学生在复杂物理情境中的数学分析能力［J］.物理教学探讨，2022，40（12）：7276.

［18］LINN M C.Gender，Mathematics，and Science［J］.Educational Researcher，1989，18（8）：1727.

［19］BURBULES N C，LINN M C.Response to contradiction：scientific reasoning during adolescence.［J］.Journal of Educational Psychology，1988，80（1）：6775.

［20］王南方，冯秀梅.物理学习态度中的性别差异及其应对策略研究［J］.物理教师，2011，32（12）：68.

［21］冯秀梅，包雷，余子侠.中美大学生科学推理能力的性别差异探讨［J］.高等教育研究，2013，34（7）：7074.

［22］李梦宇，李建彬，胡象岭.高二学生科学推理能力现状调查［J］.物理教师，2018，39（9）：1821.

Research on the Evaluation of Scientific Reasoning Abilityof Science Students based on Rasch Model

CHENG Chaojuan，ZHU Qiaoping

（College of Physics，Ningxia University ，Yinchuan Ningxia 750021，China）

Abstract：Scientific reasoning is an important part of scientific thinking.Based on Rasch model，LCTSR 2000 is employed to evaluate the scientific reasoning ability of 419 science students.The quality of scale and the development of scientific reasoning ability of subjects are also analyzed.The study shows that the dimensional development of scientific reasoning ability of science students is not balanced；scientific reasoning ability has a low positive correlcotion with academic achievement;the scientific reasoning ability of male students is slightly higher than that of female students，and there is no significant gender difference in scientific reasoning ability.Based on the empirical findings，the main reasons that affect the development of scientific reasoning ability are discussed and corresponding teaching suggestions are put forward.

Keywords：Rasch model；scientific reasoning ability；quality analysis；evaluation research；teaching suggestions