基于粒子群算法和注意力机制的LSTM的PM2.5预测研究

冀东 刘祖涵 王莉莉 涂翔

摘要：PM2.5是空气质量的重要影响因素之一，更加准确地预测PM2.5的含量，对于预报空气质量变化、空气治理和促进科学绿色发展都有着重要的作用。本文提出一种基于粒子群算法和注意力机制的长短期记忆网络（LSTM）模型，该模型既具备了LSTM可以轻松提取数据的时间维度信息的能力，又具备了注意力机制可以完美解决特征权重分配的能力，可以较为准确地对空气中PM2.5含量进行预测。通过与K近邻回归、支持向量回归、循环神经网络和未进行寻优处理的基于注意力机制的LSTM等模型进行对比试验，证明了基于粒子群算法和注意力机制的LSTM在预测空气中PM2.5含量时具有更佳的性能，且模型的均方误差（MSE）、平均绝对误差（MAE）在保证相同相关系数（R2）的情况下，降低了50%以上。

关键词：PM2.5；长短期记忆网络；注意力机制；粒子群算法；预测

中图分类号：X513；TP183文献标志码：A文章编号：1673-5072（2024）03-0327-08

随着社会的不断发展，中国的城市化进程不断加速，但在此过程中，却带来了很严重的空气环境污染［1］。空气环境的污染主要以空气质量来反映，而影响空气质量主要分为环境气象因素和空气成分因素［23］。常见的空气污染物包括可吸入颗粒、SO2、NO2、CO、O3等，其中可吸入颗粒根据颗粒直径又可以划分为PM100、PM10和PM2.5，由于颗粒物直径的大小不同，这些颗粒物在空气中的存在时间也不相同，直径越小的颗粒物在空气中存在时间越长，因此PM2.5在空气中悬浮的时间最长。又因为PM2.5不仅体积小，同时又含有大量有毒物质，所以对心肺疾病的致病率也就越高［4］。因此，准确地预测PM2.5对预测空气质量和人类健康生活都极其重要。

预测PM2.5的方法主要有两类：第一类是基于数学物理方法的模型，其优点是可以进行小范围空气预测，适用于工厂的空气污染监测，缺点是不适用于城市的预测［5］。第二类是数据驱动的模型，分为机器学习和深度学习。机器学习的模型如K近邻模型、支持向量机模型、极限学习机模型，这类模型可以根据不同城市中的PM2.5数据先进行学习，再对空气中的PM2.5进行预测，优点是简化了特征工程的处理，但是对高非线性问题处理效果不佳［68］。深度学习模型，例如卷积神经网络、循环神经网络［9］（Recurrent Neural Network，RNN），在预测非线性的时序问题时都有很好的效果，但循环神经网络以其处理时间序列的优秀能力，在时序预测问题上得到了很广泛的应用［10］。但是，在实际的神经网络训练过程中发现RNN对数据无法做到长期保存，在之后的不断训练过程中还发现原始的RNN存在梯度消失和梯度爆炸的问题，这两种问题的出现限制了循环神经网络的实际应用［11］。而长短期记忆网络（Long ShortTerm Memory Network，LSTM）作为RNN的一种改进模型，它通过增加记忆单元方法，使网络可以保留长期记忆和调节反向传播中权重参数的更迭，这样不仅继承循环神经网络优秀的时间序列处理能力，还解决了RNN的梯度不稳定的问题。在此基础上，Pranolo等［12］和Cen等［13］为了避免根据主观经验选择超参数的缺点，都使用不同的粒子群算法（Particle Swarm Optimization，PSO）与LSTM进行结合对空气质量进行预测，使LSTM模型可以自主调整模型的超参数，减少了人工调试的成本。Dong等［14］使用注意力机制的方法构建了以LSTM为基础的模型，实现了更加集中地提取PM2.5数据中的有效信息。然而，上述方法都只单一解决了LSTM网络对信息中某种特征的提取，但实际上，数据信息所包含的特征是复杂的，因此对预测也有着显著的影响。

为了进一步提高对空气中PM2.5含量的预测能力，首先，采用LSTM为基础模型，加入注意力机制，合理分配了神经网络中的参数权重，在训练参数时，根据关注度的大小有偏重地对特征进行训练，使神经网络在时序预测问题上拥有更高的预测精度；其次，使用PSO对网络中的超参数进行寻优，进一步优化网络结构，使网络模型拥有最佳的网络超参数；最后，实现对PM2.5的精准预测。

1数据来源和预处理

1.1数据来源

数据集来自加利福尼亚大学尔湾分校的机器学习数据库时间序列分库中的空气污染数据。数据集中以每小时记录一次的频率展示了北京昌平地区自2013年3月至2017年2月的空气质量信息。数据集中包括了PM2.5、PM10、SO2、NO2、CO、O3等污染物信息和温度、湿度、压强、降雨和风速等环境信息。

1.2数据的影响关系与预处理数据间的关系：PM2.5的含量在空气质量监测中受很多因素影响，例如：季节、温度、湿度等环境因素和氮、碳、硫与氧气化合形成的各种化学颗粒物。其中，PM10、SO2、NO2、CO、O3浓度与PM2.5浓度存在显著正相关特性［15］。由此在数据集中选择PM10、SO2、NO2、CO、O3、PM2.5浓度这6项作为主要参数数据。

试验数据的预处理：整个数据集有35 063条数据，首先按照测试集为9∶1对数据进行划分。因为数据进

行格式变换传入网络时，需要将网络中的所有数据改成数值浮点型，所以在数据集中出现了缺失值时，就需要对缺失值进行处理。处理方法有删除和插补两种方法，由于缺失值相对于整个数据集来说并不多，所以采取将缺失值所在行进行删除处理。这个处理方法不仅相对简单，而且在试验中，由于删除缺失值相当于神经网络中的Dropout操作，使神经网络可以应对更复杂的变化，减少过拟合现象。其次，在输入序列时若输入数据的时间间隔太大则对细节不能很好预测，序列太短又容易出现较多的异常值，因此，以每5 h的时间数据为一个输入序列的小样本，作为一个小的时序信号，将6項主要参数数据作为时序数据预测的6项输入特征，形成一个5×6的时序矩阵（图1）。最后，对输出数据而言，为了检测序列预测的优劣，以下一时间步的PM2.5特征作为预测结果优劣的评定。

2研究方法

2.1长短期记忆网络LSTM是RNN的改进模型［1618］，是深度学习中能够处理时序问题的重要模型，RNN由输入层、隐藏层和输出层3层和1个延迟器组成，RNN的基本组成和沿时间展开如图2所示。根据图2可知循环神经网络的输出和隐藏层的迭代公式为：

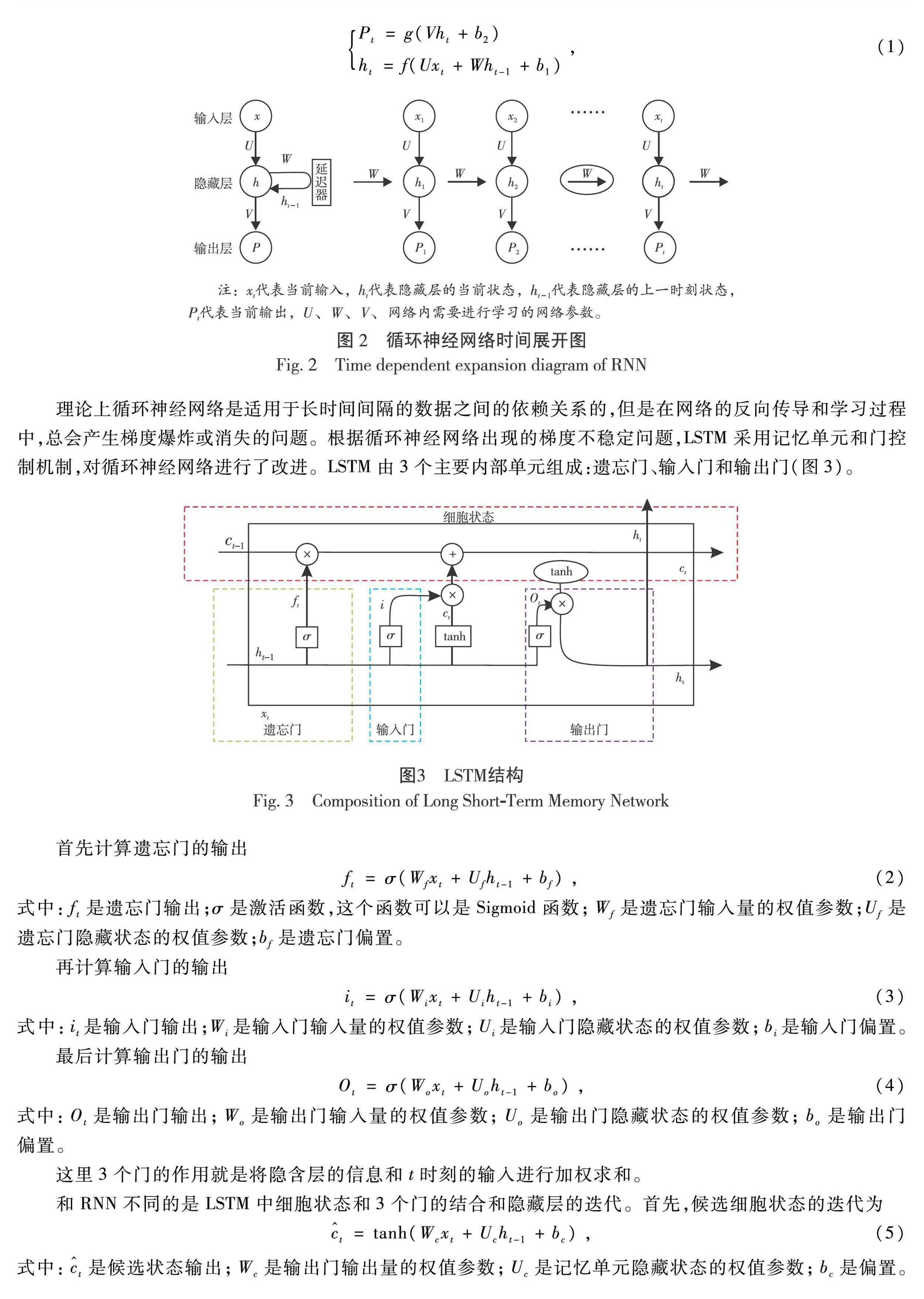
理论上循环神经网络是适用于长时间间隔的数据之间的依赖关系的，但是在网络的反向传导和学习过程中，总会产生梯度爆炸或消失的问题。根据循环神经网络出现的梯度不稳定问题，LSTM采用记忆单元和门控制机制，对循环神经网络进行了改进。LSTM由3个主要内部单元组成：遗忘门、输入门和输出门（图3）。

首先计算遗忘门的输出

式中：ft是遗忘门输出；σ是激活函数，这个函数可以是Sigmoid函数；Wf是遗忘门输入量的权值参数；Uf是遗忘门隐藏状态的权值参数；bf是遗忘门偏置。

再计算输入门的输出

式中：it是输入门输出；Wi是输入门输入量的权值参数；Ui是输入门隐藏状态的权值参数；bi是输入门偏置。

最后计算输出门的输出

式中：Ot是输出门输出；Wo是输出门输入量的权值参数；Uo是输出门隐藏状态的权值参数；bo是输出门偏置。

这里3个门的作用就是将隐含层的信息和t时刻的输入进行加权求和。

和RNN不同的是LSTM中细胞状态和3个门的结合和隐藏层的迭代。首先，候选细胞状态的迭代为

式中：c^t是候选状态输出；Wc是输出门输出量的权值参数；Uc是记忆单元隐藏状态的权值参数；bc是偏置。

得到了细胞单元的候选状态后再进行对细胞状态的迭代

式中：ftct－1表示上一时刻的细胞状态ct－1保留到当前时刻ct的数量；itc^t表示了当前时刻网络的输入xt保存到细胞状态ct的数量。

2.2注意力机制在神经网络处理信息时，根据输入数据的特征进行处理，而输入的大量特征中，根据影响程度不同，各个特征的重要程度也不同。注意力机制就是选择关键性数据赋予高比例特征值权重，来提高神经网络处理信息的效率［19］。在LSTM中，注意力机制根据时序信息中不同特征进行加权，可提高神经网络预测的相关度。

注意力机制的本质如图4所示。在神经网络内部加入一个线性转换节点，对输入神经网络的数据特征进行注意，然后按照注意力的分布不同，给予不同的分配权重，公式解释为

式中：L为输入序列，q代表特征，αi是注意力分布，li是序列中的第i个信息。

2.3粒子群算法粒子群算法是一种群智能算法［20］，以每个粒子的学习经验来不断地搜索最佳的探索方向，进而找出给定范围的最优解。粒子群算法的运行流程首先是对粒子群进行初始化，从各个粒子的适应值中选择局部最优（Personal Best，PB）和全局最优（Global Best，GB），再设置最大迭代次数和计算粒子当前位置的误差函数，进行速度S和位置向量Z的更新，计算出新的局部最优和全局最优，当迭代次数达到最大迭代时输出全局最优解。粒子群算法的速度和位置的迭代公式为

式中：g1、g2和ω分别是算法中的学习因子和惯性因子，它们影响了算法搜索的收敛速度和鲁棒性，并且不同大小的惯性因子也能影响局部与全局优化能力。r1、r2为0到1之间随机数，它们影响了算法搜索的随机性。

3试验

3.1试验环境试验使用计算机硬件配置：CPU为i512500；显卡为RTX3070，显存8G。计算机软件配置：Windows11操作系统，TensorFlow为2.3GPU版本；NumPy为1.18.5版本，Pandas为1.3.5版本。软件平台为PyCharm64位公开版，神经网络基于Keras（2.4.3版本）深度学习框架进行搭建。

3.2试验流程首先创建基于粒子群算法和注意力机制的LSTM神经网络模型（PSO LSTMATT），在这个神经网络模型里，将神经网络中神经元个数、批大小和训练代数这3个重要的参数以未知的参量进行代替；其次使用PSO对这3个参数在合理的区间内进行寻优，寻优过程以真实值和预测值的均方误差（MSE）为目标函数，求解当MSE最小的时候，神经网络中超参数的值；然后以这3个寻优后的参数带入原网络中进行训练，以测试集的获取得到预测值；最后将测试集中真实值和预测值进行评估，过程如图5。

3.3试验结果本次试验中，以K近邻算法（KNN）、支持向量机算法（SVR）、RNN、LSTM、基于注意力机制长短期记忆网络（LSTMATT）和基于粒子群算法的长短期记忆网络（PSOLSTM）等6种不同的模型和本文模型PSOLSTMATT进行对比试验。由于样本量太大，在图像分辨时真实数据的曲线和预测数据的曲线之间的差距就不太明显，所以下面试验用图（图6）只记录100条数据的曲线变化来更加清晰地展示预测和实际之间的差距。由图6中可知KNN模型和SVR模型可以较好的进行预测，但是离准确预测PM2.5浓度还有差距，而其他5种添加了注意力机制的神经网络模型能更加准确的预测拟合曲线。另外从LSTM模型和PSO-LSTM模型的预测曲线图可知，当进行了PSO寻优后模型都具有一定的优化作用的。使用回归决定系数（R2）、MSE、MAE 3种评估指标对7种模型进行评估，评估结果见表2。

如表2所示，KNN和SVR这2种机器学习方法在所有模型中的表现处于中等，MAE、MSE和R2分别为8.10和12.37、366.04和596.08、0.93和0.89。因为对PM2.5含量预测的时间序列预测问题是一个高度非线性的问题，所以擅长解决非线性问题的深度学习方法就在时间序列预测问题上有了大展身手的机会。但是在试验中，RNN和LSTM的预测性能并不好，它们的MAE、MSE和R2分别为25.38和24.13、1 605.63和1 39321、0.46和0.63。這是因为在神经网络模型中，模型的参数量越大，对试验的影响也就越大。因此在神经网络中，对于时间序列中的各个特征的权重就更加难以进行训练。

加入注意力机制可以加速神经网络中特征权重的训练。LSTMATT模型的MAE、MSE和R2的分别为110、3.79、0.99。在加入了注意力机制后，对特征权重的注意力分布如图7所示，根据注意力机制对于不同污染物质的注意程度，提升了神经网络对空气环境中各个污染物质的检测的灵敏度，增强了神经网络对分析各个污染物质在不同时间段上影响空气质量的联系，进一步强化了网络在大数据统计下的数据关联，提高了网络的预测能力。

图7（a）中神经网络的神经元个数、批大小、训练代数都是固定的，在未寻优之前，采用和LSTM相同的网络超参数进行训练以达到控制变量。寻优之后，搜索出最佳配比的超参数，进行预测后，得到最佳的注意力分布图7（b）。根据最新的特征权重进行预测后，它们的MAE、MSE和R2分别0.46、060和0.99。对比发现，在保证了相关系数的情况下降低了MAE和MSE。经过PSO进行寻优后网络的神经元数、批大小和训练代数由原来的32、50和72变化为25、49和12。神经元数降低了约25%，大大减少了网络的训练参数，加快了网络训练进程；而批大小的变小，预测数据的变化会更加平滑，训练代数降低了60代，模型误差可以更早的收敛，从而减小了MSE、MAE的值，相比于未进行优化的模型，优化模型的MSE、MAE降低了超过50%。

4结论

精确的PM2.5含量预测结果可以为空气质量的预测提供数据基础，以便提前采取不同的措施对空气质量进行治理，改善城市空气，促进社会的健康绿色发展，也能给健康出行提供参考。目前在相关的研究中，鲜少对神经网络进行参数寻优，但是神经网络的超参数对预测结果准确性和预测平稳性都有着较大的影响。针对这个问题，本文建立了一个基于粒子群算法和注意力机制的LSTM模型来预测空气中的PM2.5含量，并且对比了SVR、KNN、RNN等不同预测模型。从不同模型来看，基于注意力机制的LSTM拥有更好的预测结果。本文的主要贡献在于在使用了粒子群算法后，解决了模型中神经元等参数固定的问题，使网络结构更加稳定，网络预测更加平缓。进行优化后的模型对原联合模型拥有更佳的预测能力，在预测空气中PM2.5含量时有更好的准确率。

在后续的研究中，可以选取双向网络来搭建基础网络，根据双向网络对过去未来双向时间的特征处理能力，挖掘出数据特征在过去未来时间中的关系，来构建预测模型。例如，前后两天的天气之间是相互影响的，PM2.5的含量变化也会根据积累和扩散相应变化。对于数据噪音的不同，本文使用对数据进行删除方法处理，未来可以考虑使用均值填充等其他方法去噪，使模型拥有更好的预测精度。

参考文献：

［1］王永红，邢艳春，郝小娇.空气污染与经济增长的空间效应及其关系检验［J］.统计与决策，2022，38（15）：7781.

［2］HAN X D，LI H J，LIU Q，et al.Analysis of influential factors on air quality from global and local perspectives in China［J］.Environmental Pollution，2019，248：965979.

［3］LIU Z H，WANG L L，ZHU H S.A timescaling property of air pollution indices：a case study of Shanghai，China［J］.Atmospheric Pollution Research，2015，6（5）：457486.

［4］杨慧，黄瑾，罗明良，等．PM2.5和PM10浓度分布的空间插值方法比较：以河南省信阳市为例［J］．西华师范大学学报（自然科学版），2023，44（6）：16.

［5］ZHENG Y，LIU F，HSIEH H P.Uair：when urban air quality inference meets big data［C］//American Computer Sociely.Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.Chicago，2013：14361444.

［6］KARPATNE A，EBERTUPHOFF I，RAVELA S，et al.Machine learning for the geosciences：challenges and opportunities［J］.IEEE Transactions on Knowledge and Data Engineering，2019，31（8）：15441554.

［7］CHU J，DONG Y，HAN X，et al.Shortterm prediction of urban PM2.5 based on a hybrid modified variational mode decomposition and support vector regression model［J］.Environmental Science and Pollution Research，2021，28（1）：5672.

［8］李濟瀚，李晓理，王康，等.基于PCAOSELM的大气PM2.5浓度预测［J］.北京理工大学学报，2021，41（12）：12621268.

［9］ZHU M，XIE J.Investigation of nearby monitoring station for hourly PM2.5 forecasting using parallel multiinput 1DCNNbiLSTM［J］.Expert Systems with Applications，2023，211：118707.

［10］LIU B，YAN S，LI J Q，et al.A spatiotemporal recurrent neural network for prediction of atmospheric PM2.5：a case study of Beijing［J］.IEEE Transactions on Computational Social Systems，2021，8（3）：578588.

［11］杨丽，吴雨茜，王俊丽，等.循环神经网络研究综述［J］.计算机应用，2018，38（S2）：16.

［12］PRANOLO  A，MAO Y，WIBAWA A P，et al.Optimized three deep learning models BasedPSO hyperparameters for Beijing PM2.5 prediction［J］.Knowledge Engineering and Data Science，2022，5（1）：5366.

［13］CEN H，YU L，PU Y，et al.A method to predict CO2 mass concentration in sheep barns based on the RFPSOLSTM model［J］.Animals，2023，13（8）：1322.

［14］DONG L，LIU J，ZHAO Y.Forecasting of PM2.5 concentration in Beijing using hybrid deep learning framework based on attention mechanism［J］.Applied Sciences，2022，12（21）：11155.

［15］劉严萍，王勇，赖迪辉.基于PM10与气态污染物的北京市PM2.5浓度模型研究［J］.灾害学，2016，31（2）：116118.

［16］ELMAN J L.Finding structure in time［J］.Cognitive Science，1990，14（2）：179211.

［17］HOCHREITER S，SCHMIDHUBER J.Long shortterm memory［J］.Neural Computation，1997，9（8）：17351780.

［18］HOCHREITER S.Untersuchungen zu dynamischen neuronalen Netzen［D］.Munich：Technische Universitt München，1991.

［19］MNIH V，HEESS N，GRAVES A.Recurrent models of visual attention［J］.Computer Science，2014，2：22042212.

［20］KENNEDY J，EBERHART R.Particle swarm optimization［C］//Proceedings of ICNN95International Conference on Neural Networks.IEEE，1995，4：19421948.

PM2.5 Prediction of Long ShortTerm Memory Network（LSTM）Based on Particle Swarm Optimization Algorithmand Attention Mechanism

JI Dong1a，LIU Zuhan1a，WANG Lili1b，TU Xiang2

（1.a.School of Information Engineering，b.College of Science，Nanchang Institute of Technology，Nanchang Jiangxi 330099，China;

2.Jiangxi Academy of EcoEnvironmental Sciences and Planning，Nanchang Jiangxi 330039，China）

Abstract：PM2.5 is one of the important factors affecting air quality.More accurate prediction of the content of PM2.5 plays an important role in forecasting air quality changes，doing air governance and promoting the scientific and green development.This paper proposes a Long ShortTerm Memory Network（LSTM） model based on particle swarm optimization algorithm and attention mechanism.This model has both the ability of LSTM to easily extract the time dimension information of data，and the ability of attention mechanism to perfectly solve the feature weight distribution，which can more accurately predict the content of PM2.5 in the air.Through comparative experiments with K nearest neighbor regression，support vector regression，recurrent neural network and LSTM based on attention mechanism without optimization processing，it is proved that the LSTM based on particle swarm optimization algorithm and attention mechanism has better performance in predicting PM2.5 content in the air，and the Mean Square Error （MSE） and Mean Absolute Error （MAE） of the model are reduced by more than 50% under the same correlation coefficient （R2）.

Keywords：PM2.5；Long ShortTerm Memory Network；attention mechanism；particle swarm optimization algorithm；prediction