层流信道中基于模型驱动的信道建模方法

王悦 鲍煦 林锋

DOI： 10.3969/j.issn.1671-7775.2024.03.009

开放科学（资源服务）标识码（OSID）：

摘要： 针对已有的层流信道模型不能直接应用于存在目标的复杂层流信道的问题，提出一种基于模型驱动的信道建模方法.研究了存在目标的层流扩散信道的系统模型，在无目标平流模型的基础上加入参数，考虑层流和目标对接收分子的影响.结合仿真结果，将有目标的复杂层流信道近似为两个稳定的层流信道，建立有目标的点源-接收机层流扩散信道模型.结合神经网络使用Levenberg-Marquardt 算法对信道模型参数进行学习和预测，同时提出基于数据和模型驱动结合（combination of data and model driven，CDMD）的检测方法对目标进行检测.结果表明：通过公式数据与仿真数据对比验证了其信道模型的准确性，所有数据的相关系数为0.999 15，该神经网络模型具有可行性；使用神经网络二分类算法验证提出的目标检测方法，检测准确率达到98.8％时，提出的CDMD检测方法所需数据量约为基于数据检测方法的1/6.

关键词：  分子通信； 层流扩散； 信道建模； 模型驱动； 神经网络； 目标检测

中图分类号： TP391.9  文献标志码：  A  文章编号：   1671-7775（2024）03-0309-07

引文格式：  王  悦，鲍  煦，林  锋. 层流信道中基于模型驱动的信道建模方法［J］.江苏大学学报（自然科学版），2024，45（3）：309-315，322.

收稿日期：   2022-10-27

基金項目：  农业农村部淡水渔业健康养殖重点实验室开放课题重点项目（ZJK202204）; 江苏省六大人才高峰高层次人才计划项目（XYDXX-115）

作者简介：   王  悦（1998—），女，江苏沛县人，硕士研究生（1220016090@qq.com），主要从事层流信道建模研究.

鲍  煦（1982—），男，江苏靖江人，教授，博士生导师（xbao@ujs.edu.cn），主要从事信号处理、物联网技术研究.

Model-driven channel modeling approach in laminar channel

WANG Yue1， BAO Xu1， LIN Feng2

（1. School of Computer Science and Communication Engineering， Jiangsu University， Zhenjiang， Jiangsu 212013， China; 2. Key Laboratory of Healthy Freshwater Aquaculture of Ministry of Agriculture， Zhejiang Institute of Freshwater Fisheries， Huzhou， Zhejiang 313001， China）

Abstract： To solve the problem that the existing laminar channel models could not be directly applied to the complex laminar channels with targets， a model-driven channel modeling approach was proposed. The system model for laminar diffusion channels with targets was extended by incorporating additional parameters in the absence of target advection models， and the effects of laminar flow and targets on received molecules were considered. Based on the simulation results， the complex laminar channel with target was approximated as two steady laminar channels， and the point-source-receiver laminar diffusion channel model with considering the presence of target was established. The Levenberg-Marquardt algorithm was employed to learn and predict channel model parameters by the neural network， and the combination of data and model driven （CDMD） detection method was proposed for target identification. The results show that the accuracy of the channel model can be validated through the comparison of formula data and simulated data with correlation coefficient of 0.999 15， which confirms the feasibility of the neural network model. The proposed target detection method can be verified by the binary classification algorithm within the neural network with detection accuracy rate of 98.8%. The CDMD-based detection method requires approximately one-sixth of the data volume needed for data-driven detection methods for maintaining high detection performance.

Key words：  molecular communication; laminar diffusion; channel modeling; model-driven; neural network; target detection

分子通信（molecular communication， MC）是使用生物化学分子作为信息载体，将纳米机器互相连接组成分布式纳米网络的短距离通信技术［1］.MC的优点有生物兼容性好、体积小、能耗低等［2］.基于MC的纳米网络广泛应用于生物医学、工业和环境保护等领域［3］.其中，分子通信结合纳米技术在生物医学领域的研究热点有靶向给药.基于纳米技术的靶向给药技术能够定向传输并定时将药物靶向输送到特定细胞中.在水下信道中，传统基于波的信号受到时间和距离影响后能量会快速衰减，搜索耗时长且成本高；而MC中基于化学编码传递消息的方法传播距离更长、信号持续时间更久，MC因这一特性可适用于远程水下污染源检测［4］.

目前有许多关于分子通信扩散信道模型的理论研究，文献［5］推导了一维有界扩散信道的信道模型，其边界（吸收或反射壁）分为对称边界和不对称边界两种情况.文献［6］针对兴奋性突触分子通信信道，推导了三维突触几何结构中神经递质扩散和结合的信道模型.文献［7］对于存在两个接收机的无界场景，在仿真数据上使用统计算法推导信道模型.上述研究主要集中在自由扩散通道中的信道模型推导，而层流扩散在实际应用中更为常见.

层流传输是MC系统宏观方向上的长距离传输机制，其沿速度场方向的流线是平行的，如在平稳流动的河流中.由于速度的存在影响分子扩散，层流信道模型较为复杂.在层流传输机制的研究中，文献［8］推导了层流介质中移动传感器协同合作的信道模型，并提出了异常检测和定位算法.文献［9］给出了有界方形层流管道信道的信道脉冲响应（channel impulse response，CIR）模型，但此模型较为复杂，在存在目标障碍物的信道中，分子信号会受到目标的显著影响，上述模型并不能直接使用.

文中拟考虑一个二维有界有目标的层流扩散场景，研究层流扩散下目标对接收机接收分子数的影响.提出模型驱动的建模方法，在原有无目标平流CIR模型的基础上推导出层流扩散下有目标的信道模型，并使用COMSOL仿真软件构建二维仿真模型，二者进行了对比；同时，将仿真得到的数据放入神经网络中使用Levenberg-Marquardt（LM）算法进行训练，并对信道模型参数进行学习及预测，以验证该信道模型的准确性.上述方法是在二维环境中提出的，但在三维环境也同样适用.得出的信道模型可应用于检测有无目标，文中提出基于数据和模型驱动结合（combination of data and model driven，CDMD）的目标检测方法，具体应用场景包括城市地下水管道、污水管道污染源检测［10］等.

1  有目标的层流信道系统模型

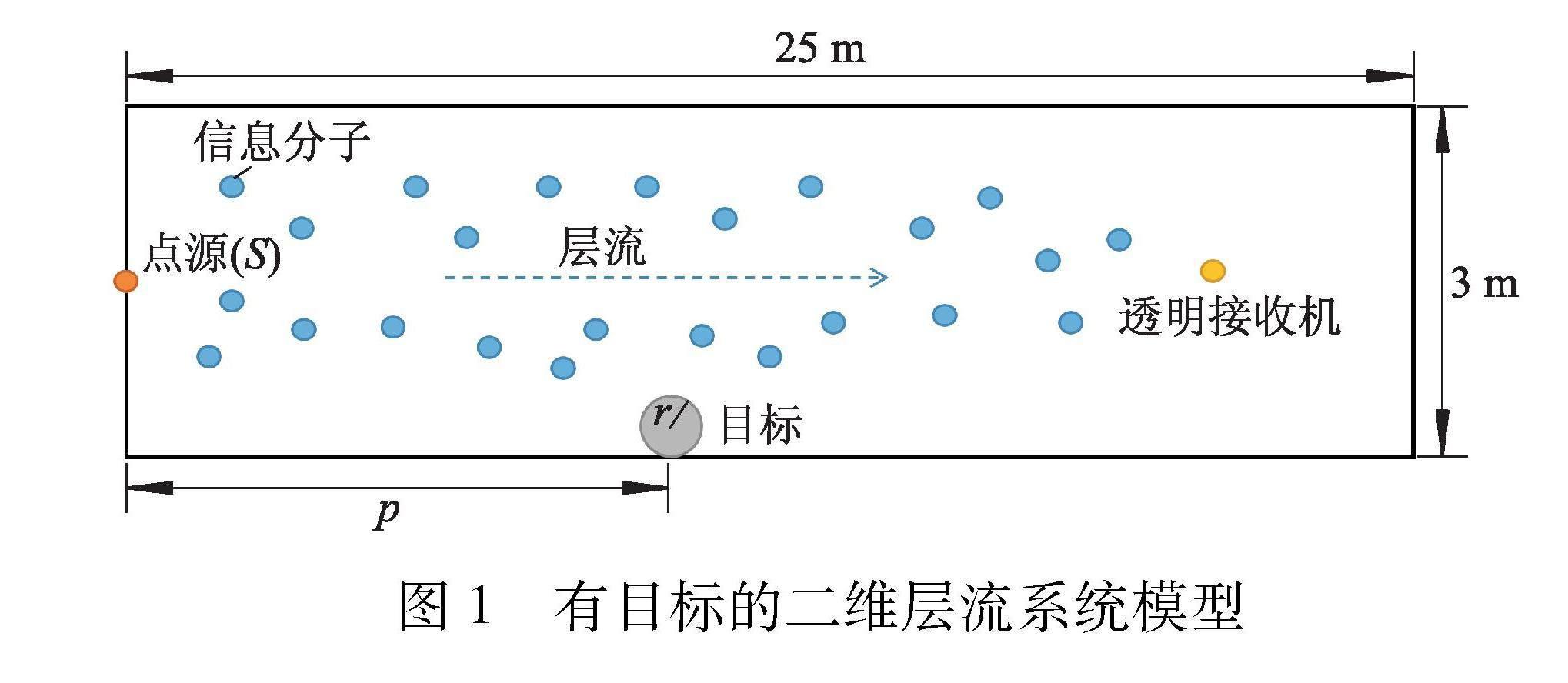
图1给出了有目标的二维层流系统模型.

由图1可见，二维层流信道中包含一个点源S、一个圆形目标和一个接收机.二维层流信道长25 m，宽3 m，层流流体速度为5.1 m/s，信息分子在层流的流动下传播，边界是完全反射的.点源S放置在模型左侧的中心位置，在初始时刻瞬间释放2 mol/m3的信息分子，其形状不会对模型产生影响，因此，无需考虑信息分子产生和释放对CIR的影响.目标为圆形障碍物，位于二维层流信道的下边界，半径r为0.4 m，目标圆心距点源的水平距离p为10 m，既不释放分子也不吸收分子，信息分子遇到目标之后发生反射，存在目标会改变层流信道中的流体方向以及速度，不同位置的目标对流体产生不同的影響.接收机的形状为一个点，作为观察接收机，放置在水平方向据点源15 m的中心位置，只观测分子浓度，不影响分子扩散.

文中使用COMSOL Multiphysics来获取仿真数据，该软件提供了多物理场建模和仿真解决方案，其中计算流体动力学仿真模块可提供层流模型，利用该模型可以对稳态或瞬态的层流进行仿真获取各点信息分子的浓度［11］.实际上，通过COMSOL模拟获得的仿真浓度数值近似于大量试验的平均值，而并非某一次试验的结果［12］.

COMSOL获取的数据集Dd=Dd1+Dd2为接收机得到的浓度信息，共2 000组数据，其中有无目标各1 000组.无目标数据集Dd1、有目标数据集Dd2组成如下：

Dd1=（t，ct，v，L，q，m）

t=0，0.1，0.2，…，13.5 s，

v=5.1，5.3，…，6.1 m/s，

L=1.2，1.3，…，1.5 m，

q=11，12，…，18 m，

m=-1，-0.5，…，1 m，（1）

Dd2=（t，c′t，v，L，p）

t=0，0.1，0.2，…，13.5 s，

v=5.1，5.3，…，6.1 m/s，

L=1.2，1.3，…，1.5 m，

p=6.0，6.25，…，11 m，（2）

式中： 为模拟信道中的噪声，层流流速v为5.1～6.1 m/s，步长为0.2 m/s；ct为无目标时接收机在t时刻的浓度值；c′t为有目标时接收机在t时刻的浓度值；定义点源为原点位置，q为接收机的水平坐标；m为接收机的垂直坐标.通过MATLAB命令设置COMSOL中边界大小、目标的位置及接收机的位置获得数据集Dd.仿真参数设置如下：点源发射机初始浓度c0为2 mol/m3；仿真区域长度X、宽度2L分别为25、3 m；仿真步长Δt为0.1 s；仿真总时长t为13.5 s；层流速度v为5.1 m/s；目标半径r为0.4 m；目标圆心距点源水平坐标p为10 m；扩散系数D为10-10 m2/s；水的动力黏度μ为10-3 pa·s；水的密度ρw为1 000 kg/m3；接收机水平方向坐标q、垂直方向坐标m分别为15、0 m.

COMSOL仿真得到浓度分布见图2，其中圆形目标的半径r=0.4 m，圆心坐标为（10，-1.1） m.由图2a可见，信息分子未经过圆形目标时，浓度分布整体呈基本对称的趋势，中心位置浓度值最大，浓度值由内部向两侧递减，浓度峰值为1.79 mol/m3.由图2b可见，当信息分子经过圆形目标后，浓度分布整体向上移动，浓度峰值为1.68 mol/m3，信息分子浓度值整体呈不对称趋势，仍由内向外递减.

COMSOL仿真得到速度分布见图3.

由图3a可见，信道中无目标时流速整体呈对称分布，层流速度恒定在8.0 m/s，由于边界的影响，边界位置的流速呈递减分布.在图3b所示的信道中，放置一个半径r=0.4 m，圆心坐标为（10，-1.1） m的圆形目标.层流经过圆形目标前，流速整体基本呈对称分布，流速恒定在5.1 m/s.流体经过目标后，流速关于目标呈上下分层分布，目标上方位置的流体速度明显增大，并持续保持这个速度，速度最快为8.1 m/s，距离目标越远时，流速逐渐减小，从目标位置到靠近下边界的层流流速基本为0.

2  公式拟合及结果分析

CIR定义为端到端信道特性，用h（t）表示.对于带有接收机的分子通信系统，CIR可以看作是接收机内一个分子的观测概率［13］.如果系统中只有一个脉冲点发射器和一个接收机，则h（t）可表示为

h（t）=14πDtexp-x2-y24Dt.（3）

佩克莱数（Peclet number，简称Pe数）是在连续传输现象研究中经常用到的一个量纲为一的数，其物理意义为对流速率与扩散速率之比：

Pe=d2c/Ddc/v=vdcD，（4）

式中： dc为扩散长度.如果Pe<<1成立，信息分子运动由扩散主导，尽管沿流动方向有微弱的偏向传输，信息分子的扩散几乎是各向同性的，此时，CIR为h（t）；如果Pe>>成立，信息分子运动由平流流动主导，此时，CIR为hA（t），在二维无界平流场景中，hA（t）可表示为

hA（t）=14πDtexp-（x-vt）2-y24Dt.（5）

定义在二维有界自由扩散场景中，点源位于左边界中点，接收机在坐标（x，y）、时刻t观察到的一个输出分子的概率为h∧（t）.当信道模型有边界时，信息分子不是自由地跨边界扩散，而是碰撞边界反射回信道.由于边界反射留在信道中的信息分子可以通过图4反射跨边界的镜像过程来解释.

由镜像法得出的h∧（t）可表示为

h∧（t）=14πDtexp-x24Dt∑+∞a=-∞exp-（y+2aL）24Dt，（6）

式中： a为反射次数.a为正数，表示分子碰撞上边界发生反射；a为负数，表示分子碰撞下边界发生反射；a为0，CIR即为无界自由扩散场景中的h（t）.

由式（5）、（6）可以得出点源位于左边界中点的二维有界平流信道的CIR为

h∧A（t）=14πDtexp-（x-vt）24Dt×

∑+∞a=-∞exp-（y+2aL）24Dt.（7）

速度是判别平流和层流的关键因素.平流流体信道中各处的速度均匀，大小相等，层流信道中间位置速度较大，边界速度较小［14］.在h∧A（t）中引入调节参数k1、k2，得出点源位于左边界中点的二维有界层流信道CIR为

h∧LF（t）=k14πDtexp-（x-vt）24Dt×

∑+∞a=-∞exp-（y+2aL）24Dt-k2，（8）

式中： k1调节峰值大小，速度是影響k1的主要因素；k2调节波形拖尾，与速度、边界宽度、时间有关，具体数值取决于有界层流信道场景.文中使用LM算法估计k1和k2的数值，并使用机器学习算法学习及预测数据来获取参数.CIR为接收机接收到一个分子的概率，点源瞬间释放2 mol/m3信息分子时，无目标时接收机接收到的分子浓度ct=c0h∧LF（t）.

选取无目标时两组场景，对比了仿真数据与公式拟合数值，结果见图5.

由图5可见，公式计算的数值与仿真结果曲线高度吻合，表明公式拟合结果与仿真结果的一致性.将图5中两种场景的变量代入式（8），得到峰值时间tpeak，其值与仿真数值匹配.通过对h∧LF（t）求导可以得出tpeak与速度v呈反比，从图5中可以看出v越大tpeak越小.2L为边界宽度，L影响浓度大小，L越大接收到的浓度越小.综上，证明了CIR模型的有效性和正确性.

he（t）为文献［10］中有界方形层流管道CIR的二维形式，计算式为

he（t）=14πDtexp-x24Dt×

∑+∞a=-∞exp-Da2π2t4L2cosaπy2L.（9）

图6给出了无目标时仿真与式（9）拟合对比.

从图6可见已有的层流式（9）与仿真数据误差较大，与图5对比可以看出文中通过镜像法拟合得出的层流式（8）更准确.

h∧LF（t）为无目标时二维有界层流信道的CIR，在信道中加入圆形目标，目标的存在会改变层流信道中速度的大小及分布趋势，信道整体不再是一个均匀的层流信道.由图3的仿真速度分布可以将整体的层流信道近似划分为两个速度分布不同的层流信道进行分析，把目标前的层流信道作为信道1，把从目标位置开始的层流信道近似为信道2，如图7所示.

在层流信道1中，流速v1=v，信道长度、宽度分别为x1、2L，信息分子在层流信道1中流动的时间为t1，即为层流信道1末端浓度的峰值时刻.在层流信道2中，将信道内的流速近似看作匀速，速度分布近似为对称分布.流速v2通过接收机获得，信道长度x2为接收机的位置x与层流信道1长度x1的差值，即x2=x-x1，信道宽度2L1=2L-2r，信息分子从经过层流信道2到接收机处的时间为t2，信息分子在信道中流动的总时间为t.x的计算式为

x=v1t1+v2（t-t1），（10）

式中： x=15；v1=5.1 m/s；v2和t的值由接收机获取.

通过式（10）可以得出t1的值，并计算出x1的大小，x1=t1v1.由于层流信道2中的流速是近似均匀分布的，因此x1也为近似值，需要在式（10）添加修正参数k3和k4分别调节x1和v2的数值大小.在式（8）中，将x替换为x-k3x1，v替换为k4v2，L替换为L1即L-r.由此得出层流信道2的CIR模型为

h′∧LF（t）=k14πDtexp-（x-k3x1-k4v2t）24Dt×

∑+∞a=-∞exp-（y+2aL1）24Dt-k2，（11）

式中： k3和k4通过公式拟合的方法获得，具体数值取决于信道场景.有目标存在时接收机接收到的分子浓度c′t=c0h′∧LF（t），选取有目标时的两组场景，对比了仿真数据与公式数值，结果见图8，其拟合结果记录在表2中.

由图8可见，由于目标的存在，阻碍了部分信息分子的运动，仿真结果存在一些波动，但公式计算的数值曲线较为平滑，公式与仿真的总体趋势基本一致.其中，tpeak与速度v呈反比，满足v越大tpeak越小的趋势.p为目标圆心的横坐标，目标距点源越近，接收机接收到的浓度值越大.公式计算的数值与仿真结果曲线比较吻合，表明提出信道模型的正确性.

表1中R表示相关系数，取值范围为［0，1］，相关系数越趋近1，两个变量的关系接近正比，拟合的模型计算结果越接近实际数据，其表达式为

R=r（yi，y^i）=Cov（yi，y^i）Var（yi）·Var（y^i），（12）

式中： yi为实际值；y^i为预测值；Cov（yi，y^i）为yi和y^i的协方差函数；Var（yi）和Var（y^i）分别为yi和y^i的方差函数.

SSE（sum of squares due to error）为实际值与预测值误差的平方和，即仿真数据与拟合数据的误差平方和，表达式为

SSE=∑ni=1（yi-y^i）2，（13）

式中： n为样本数量.

RMSE（root mean squared error）为均方根误差，表达式为

RMSE=SSEn=1n∑ni=1（yi-y^i）2.（14）

表2中R和RMSE均在合理的范围内，验证了拟合的有效性.

3  神经网络训练及预测

使用拟合的方法可以估计调节参数ki，得到的信道模型也已经验证了其有效性和準确性.但使用该方法之前需要获取较多的仿真数据，分子通信信道中的数据不易获取.因此，采用神经网络方法使用仿真数据对信道模型进行学习和预测.选取BP神经网络，使用反向传播和贝叶斯正则化来处理过度学习，使用LM算法更新权值和差值.神经网络的训练数据共400组，有无目标各200组，训练子集占70%，验证子集和测试子集各占15%.输入数据为浓度值，输出为调节参数ki.

图9给出了神经网络训练过程的流程图和数据集结构.

由图9可见，每组数据的输入参数为浓度，输出参数值为ki，i=1，2，3，4，构成了不同场景的训练数据集和预测数据集.将需要训练的数据放入BP神经网络训练，在训练后的神经网络中输入浓度值就可以得到预测参数ki，i=1，2，3，4.

MSE（mean square error）是验证数据和预测数据对应点的均方误差，表达式为

MSE=RMSE2=SSEn=1n∑ni=1（yi-y^i）2.（15）

MSE越趋于0表明训练得到的关系式越正确，即训练得到的数据更接近实际数据.将验证数据集的输出参数与网络训练后进行预测得到的预测参数进行对比，结果见图10.

由图10可见，从验证子集曲线可以得出训练次数为7次时曲线收敛，达到最佳性能点，此时MSE最小；训练次数少于7次时会发生“欠拟合”，即模型拟合程度不高，没有较大程度地捕捉到数据特征；训练次数大于7次时会发生“过拟合”，此时模型会使用一些看似正确却无用的关系，导致误判.训练子集、测试子集、验证子集以及400个样本的所有数据集的相关系数曲线见图11.由图 11a-c可见，训练子集的拟合曲线与训练数据的相关性高于验证子集和测试子集.图11d中的数据包括训练子集、验证子集、测试子集，R=0.999 15，结果相关性非常强.由此可知该神经网络模型是具有可行性的.

4  目标检测

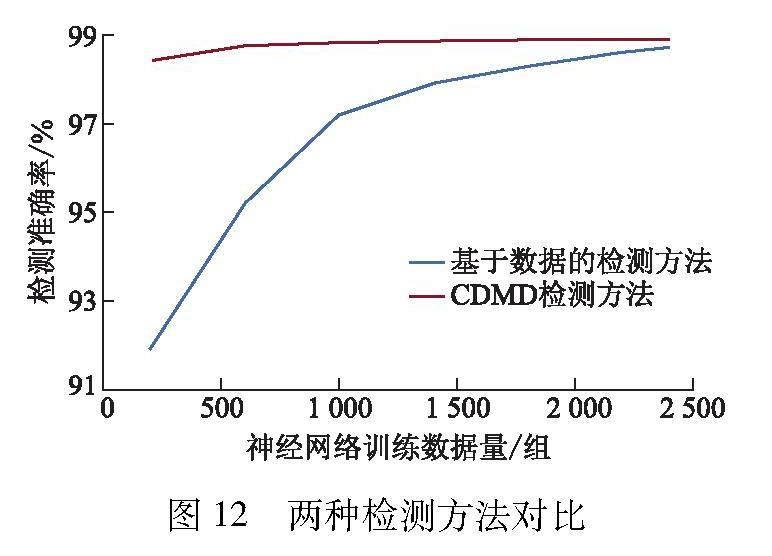
通过公式拟合和仿真试验对比验证了二维有界层流有目标信道模型的正确性，并使用神经网络的方法训练及预测新场景中的信道模型.上述模型可应用于检测目标的有无.因此，提出基于CDMD目标检测方法，使用神经网络二分类算法进行目标检测，采用400组数据，有无目标各200组，输入为浓度值，输出为无目标或有目标，分别对应数字0和1.基于数据的目标检测方法同样采用神经网络二分类算法，输入为2 400组浓度值，其中有无目标各1 200组数据，两种检测方法对比结果见图12.

由图12可见，CDMD检测方法只需较少的数据就可以得到较小的误差，数据量为400组时，检测精确率约为98.8％.基于数据的检测方法检测准确率与数据量呈正相关，数据量大于1 600组时，检测准确度大于98.0％.两种检测方法对比，检测准确率达到98.8％时，CDMD检测方法所需数据量约为基于数据检测方法数据量的1/6，该方法既可以降低对精确建模的要求，又解决了分子通信过程中不容易获取数据的问题.

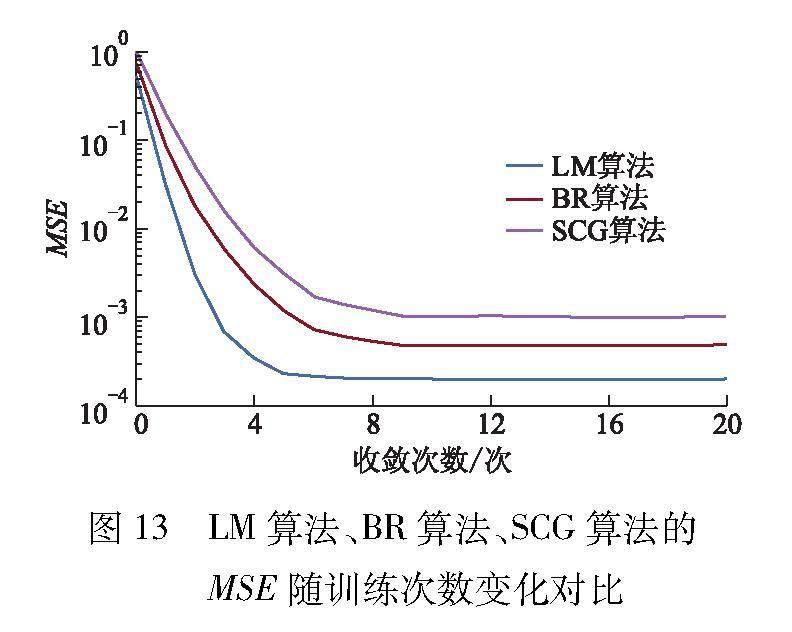
CDMD检测方法选用LM算法计算权值和差值，将LM算法与SCG算法、BR算法对比，结果见图13.

由图13可见，LM算法的收敛速度更快，对应的MSE最小，最适用于该神经网络模型的训练.

5  结  论

1） 文中提出了模型驱动的方法对二维有界层流信道进行信道建模，仿真结果验证了信道模型的准确性.提出CDMD检测方法，实现了层流信道中目标的快速准确检测.

2） 所有数据的相关系数为0.999 15，该神经网络模型是具有可行性的.

3） 同时使用神经网络二分类算法验证提出的目标检测方法，检测准确率达到98.8％时，提出CDMD的检测方法所需数据量约为基于数据检测方法数据量的1/6.

[WT5HZ]参考文献（References）[WT5”BZ]

［1］  AGHABABAIYAN K， KEBRIAEI H， SHAH-MANSOURI V， et al. Enhanced modulation for multi-users molecular communication in internet of nano things［J］. IEEE Internet of Things Journal， 2022，9（20）：19787-19802.

［2］  LI Y， LIN L， GUO W S， et al. Error performance and mutual information for IoNT interface system［J］. IEEE Internet of Things Journal，2022，9（12）：9831-9842.

［3］  CHENG Z， TU Y C， XIA M， et al. Energy efficiency analysis of multi-hop mobile diffusive molecular communi-cation［J］. Nano Communication Networks， DOI：10.1016/j.nancom.2020.100313.

［4］  LIU Y， WANG H Y， CAI L， et al. Fundamentals and advancements of topology discovery in underwater acoustic sensor networks： a review［J］. IEEE Sensors Journal， 2021，21（19）：21159-21174.

［5］  GUO W S， DENG Y S， LI B， et al. Eavesdropper loca-lization in random walk channels［J］. IEEE Communications Letters， 2016， 20（9）：1776-1779.

［6］  KHAN T， BILGIN B A， AKAN O B. Diffusion-based model for synaptic molecular communication channel［J］. IEEE Transactions on Nanobioscience，2017，16（4）：299-308.

［7］  GENC G， KARA Y E， TUGCU T， et al. Reception modeling of sphere-to-sphere molecular communication via diffusion［J］. Nano Communication Networks， 2018， 16：69-80.

［8］  KHALOOPOUR L， MIRMOHSENI M， NASIRI-KENARI M. Theoretical concept study of cooperative abnormality detection and localization in fluidic-medium molecular communication［J］. IEEE Sensors Journal， 2021，21（15）：17118-17130.

［9］  JAMALI V， AHMADZADEH A， WICKE W， et al. Channel modeling for diffusive molecular communication-a tutorial review［J］. Proceedings of the IEEE， 2019，107（7）：1256-1301.

［10］  JIN Z G， DING M G， LUO Y M， et al. Integrated time synchronization and multiple access protocol for underwater acoustic sensor networks［J］. IEEE Access， 2019，7：101844-101854.

［11］  ZHU D C， BAO X， ZHANG W C. Target recognition in turbulent diffusion channels［J］. IEEE Communications Letters， 2021，25（11）：3694-3698.

［12］  ABBASZADEH M， YILMAZ H B， THOMAS P J， et al. Linearity of sequential molecular signals in turbulent diffusion channels［C］∥Proceedings of the 2019 IEEE International Conference on Communications. Piscataway：IEEE， DOI：10.1109/ICC.2019.8761812.

［13］  BAO X， SHEN Q F， ZHU Y F， et al. Relative localization for silent absorbing target in diffusive molecular communication system［J］. IEEE Internet of Things Journal， 2022，9（7）：5009-5018.

［14］  李開勇，赵波，王翼鹏，等.有吹吸速度的外掠多孔平板湍流边界层的积分方法［J］.四川大学学报（自然科学版），2021，58（2）：155-160.

LI K Y， ZHAO B， WANG Y P， et al. The integral method for turbulent momentum boundary layers on a porous plate with uniform blowing and suction［J］. Journal of Sichuan University（Natural Science Edition）， 2021，58（2）：155-160.（in Chinese）

（责任编辑  梁家峰）