基于FPCB绕组的导管泵用电动机设计及损耗分析

王芳群 钱锋 高宇 李子健 王少俊

DOI： 10.3969/j.issn.1671-7775.2024.03.013

开放科学（资源服务）标识码（OSID）：

摘要： 基于无槽无刷直流电动机具有体积小、功率密度高、无齿槽转矩的特点，采用柔性印刷电路板（FPCB）技术设计了一种导管泵用无槽无刷微型直流电动机，提出了基于3D多物理场耦合模型分析方法，对导管泵用无槽无刷微型直流电动机进行了损耗分析和优化设计.结果表明：导管泵用无槽无刷微型直流电动机的铜损占整个电动机损耗的88%左右，是导致电动机发热的主要原因；在温度场仿真中，温度变化会改变电动机损耗，影响电动机输出转矩；在流场仿真模型中，电动机温度会使人体血液温度升高，影响血液相容性；流动的血液会带走部分热量，降低电动机温度；绕组优化后的导管泵用电动机输出转矩得到提高，损耗得以降低.

关键词：  无槽无刷直流电动机； 导管泵； 柔性印刷电路板； 多物理场； 血液相容性

中图分类号： TM385  文献标志码：  A  文章编号：   1671-7775（2024）03-0337-09

引文格式：  王芳群，钱  锋，高  宇，等. 基于FPCB绕组的导管泵用电动机设计及损耗分析［J］.江苏大学学报（自然科学版），2024，45（3）：337-345.

收稿日期：   2021-10-15

基金项目：  国家自然科学基金资助项目（51677082）

作者简介：   王芳群（1977—），女，浙江丽水人，博士，副教授（lingo@ujs.edu.cn），主要从事人工心脏泵、永磁无刷直流电动机的设计与控制的研究.

钱  锋（1990—），男，江苏丹阳人，硕士研究生（13606103415@163.com），主要从事微型导管泵用电动机的研究.

Design and loss analysis of catheter pump motor

based on FPCB winding

WANG Fangqun， QIAN Feng， GAO Yu， LI Zijian， WANG Shaojun

（School of Electrical and Information Engineering， Jiangsu University， Zhenjiang， Jiangsu 212013， China）

Abstract： Based on the characteristics of slotless brushless DC motor with small size， high power density and cogging torque， the slotless brushless micro DC motor for catheter pump was designed using flexible printed circuit board （FPCB） technology， and the loss analysis and optimal design of slotless brushless micro DC motor for catheter pump were conducted based on 3D multi-physical field coupling model analysis method. The results show that the copper loss of the slotless brushless micro DC motor for catheter pump accounts for about 88% of the whole motor loss， which is the main source of motor heating. In the temperature field simulation， the temperature change can change the motor loss and affect the motor output torque. In the flow field simulation model， the motor temperature can increase the human blood temperature and affect the blood compatibility. The flowing blood takes away part of the heat and reduces the motor temperature. The output torque of the pump motor with optimized winding is improved， and the loss is reduced.

Key words：  slotless brushless DC motor； catheter pump； flexible printed circuit board； multi-physical field； blood compatibility

導管泵是一种植入主动脉或左心室用于短期辅助治疗严重心衰的微型人工心脏泵.同时，导管泵出口位于动脉窦位置，因此还可以提高冠状动脉输出量和辅助支架的植入.为了便于植入患者体内，导管泵用驱动电动机首先要满足微型化的要求.且由于高速旋转的电动机表面与血液直接接触，过高的电动机温度会导致血液损伤.因此，导管泵用电动机同时需要满足血液相容性的要求.而血液相容性问题主要与电动机的损耗密切相关.

无槽无刷直流（BLDC）电动机相较于传统电动机具有高转速、调速性能好、高效率、体积小、结构简单、起动转矩大、功率密度高及控制性能稳定等优点，因而将其作为导管泵用驱动电动机.由于柔性电路板具有良好的柔韧性，便于采用翻折、卷曲等方式封装入电动机内部，可以大幅减小电动机尺寸和体积.本研究中，拟采用柔性印刷电路板（FPCB）代替电磁元件中传统的有线绕组，从而实现更紧凑的电动机结构设计，满足导管泵微型化要求［1］.相较于传统空心杯绕组导线工艺，FPCB绕组导线结构和绕组形状灵活性更高，且FPCB工艺较为成熟，便于加工.

电动机的温升问题涉及多个物理场，相互之间的影响十分复杂.微型电动机在有限空间内比普通电动机具有更高的电磁负载和热负载.准确计算电动机各部件的损耗，是计算电动机温升分布的关键.目前比较经典计算定子铁耗的方法是建立Bertotti铁耗分立计算模型.定子绕组基本铜损可以通过已知的绕组电流和电阻计算得到，绕组的高频涡流损耗也可以通过解析法求得.电动机温度的升高会影响到电动机材料的性能，使各部件的损耗发生变化，进而使温度发生变化.同时，电动机温度的变化会影响到血液的性质，而血液性质的变化又会影响到温度的变化.因此，在设计和制造电动机时，不仅要考虑电动机本体的工作潜力和功率密度的提高，还要考虑电动机的损耗情况.这些都是考虑电动机设计的重要方面，也是实现电动机高可靠性的关键.

目前，国内外已经开展了关于高速永磁电动机电磁场的温度场和流场的研究.文献［2］比较了三维计算模型与二维计算模型之间的差距，三维模型更能真实地模拟实际电动机，得到与实际电动机相接近的磁通密度分布及损耗值.文献［3］以损耗定值形式施加到温度场中，即损耗与温度间单向耦合，温度场分析方法以单向耦合为主，并没有考虑到温度变化对材料特性的影响.文献［4］通过流固耦合法对电动机三维模型进行了热分析，但没有考虑损耗在电动机运行过程中的变化对温度的影响.文献［5］虽然进行了流场仿真计算，但是没有明确说明流-固交界面哪些参数相互影响，且耦合后的模型过于复杂，计算结果受构建节点数的影响.

为了能准确计算电动机的损耗和温升分布，针对基于FPCB绕组的导管泵用新型无槽BLDC微型电动机，采用3D多物理场耦合模型进行双向耦合仿真计算，通过电磁场、温度场和流场等多物理场分析电动机的损耗、性能和电动机的温度场分布.

1  FPCB电动机结构设计方案

为简化电动机的3D模型，电动机在进行多物理场耦合分析时有以下假设： ① 永磁体的相对磁导率为1，和真空中保持一致； ② 只考虑径向磁场，不考虑轴向磁场的变化； ③ 电动机的漏磁忽略不计； ④ 建立流体域模型时，忽略血液入口与出口之间的温差； ⑤ 只考虑电动机绕组材料特性会受到温度的影响，其他部件的材料特性不受温度影响.

1.1  设计结构

采用FPCB技术，设计了一种用于导管泵的新型无槽BLDC微型电动机，其初始模型如图1所示.由图1可知：采用3相2极的结构，转子轴的表面安装了一对永磁体；菱形绕组绘制在FPCB板的正反面，在FPCB板上方添加绝缘层，以确保FPCB板卷制过程中绕组层之间的电气绝缘.

基于所设计的经皮导管泵用电动机拟植入于主动脉处，主动脉处动脉直径不超过20.0 mm.为了满足易于植入的要求，选用定子外直径不大于10.0 mm和轴向长度不大于20.0 mm的永磁同步电动机.已知电动机的外直径为10.0 mm，因此电动机的定子外半径Re为5.0 mm.为了便于计算，假设永磁体的相对磁导率μr=1.已知定子铁芯和转子铁芯的最大磁通密度Bs，max和Br，max约为其各自饱和磁通密度的90%［6］，即

Bs，max=0.9Bs，sat，

Br，max=0.9Br，sat.（1）

其中，电动机定子饱和磁通密度Bs，sat和轉子饱和磁通密度Br，sat分别为1.520 0、0.850 0 T.根据式（1）可以求出该电动机定子和转子的最大磁通密度分别为1.368 0、0.765 0 T.

电动机定子铁心最大磁通密度表达式为

Bs，max=2（Re2+Rs2）Re2-Rs2Be，（2）

式中： Be为永磁体的磁通密度；Rs为电动机的定子内半径.

转子铁心最大磁通密度表达式为

Br，max=（μr+1）Rm2-（μr-1）Rs2Rm2Be，（3）

式中： Rm为永磁体的外半径.

已知永磁体相对磁导率μr=1，代入式（3）得

Br，max=2Be，（4）

其中

Be=Rm2-Rr22（Rs2-Rr2）Br，（5）

式中： Rr为永磁体内半径.已知设计的FPCB电动机转子轴直径为1.0 mm，则永磁体内半径Rr=0.5 mm；Br为永磁体的剩磁.

由式（4）可以求出Be=0.382 4 T，将该值代入式（2）可以求得Rs=3.3 mm.由式（5）可知，永磁体的外半径Rm与永磁体的剩磁Br有关，且已知永磁体剩磁Br=1.280 0 T，代入式（5）可以求得Rm=2.2 mm.

1.2  电磁分析

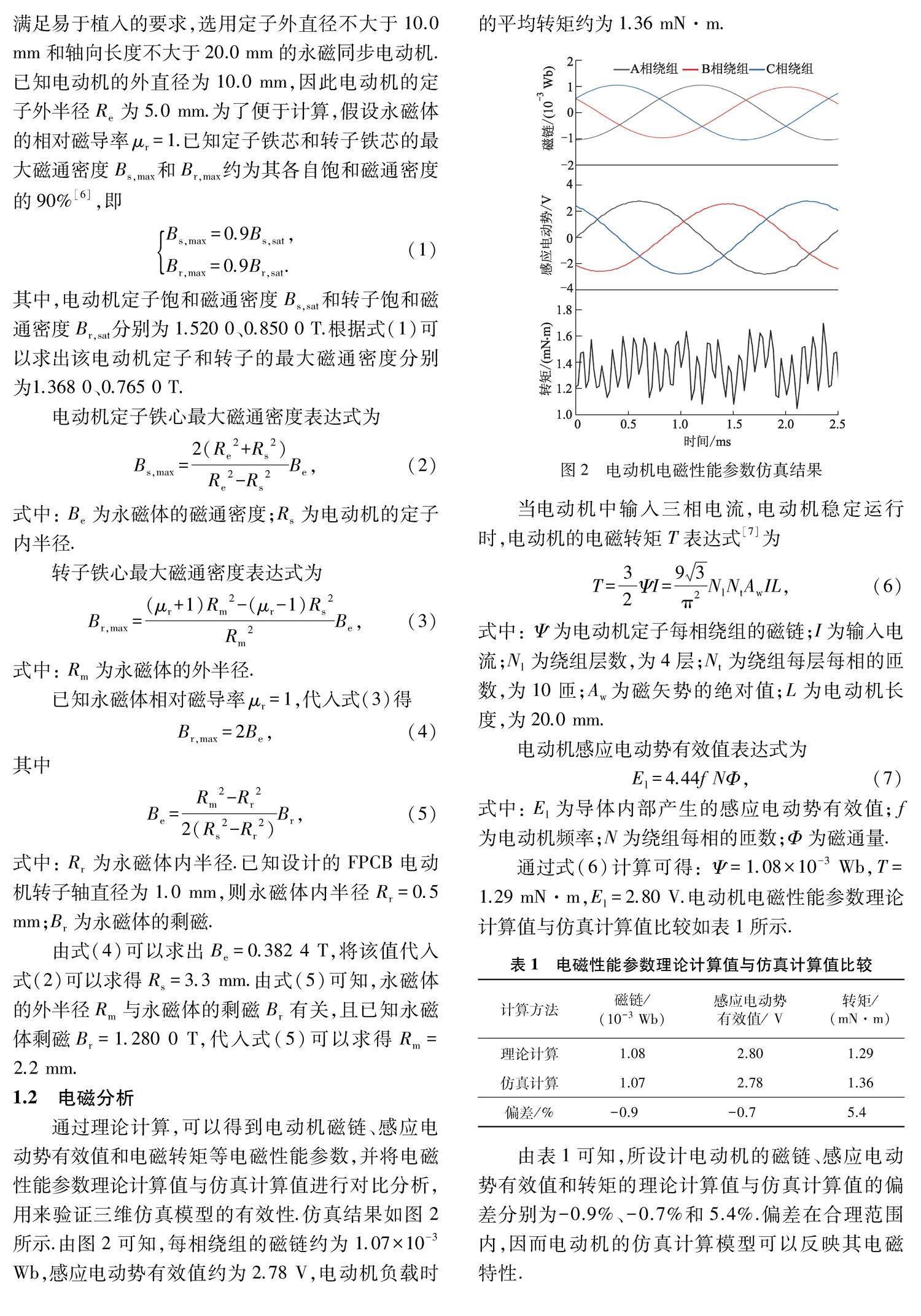
通过理论计算，可以得到电动机磁链、感应电动势有效值和电磁转矩等电磁性能参数，并将电磁性能参数理论计算值与仿真计算值进行对比分析，用来验证三维仿真模型的有效性.仿真结果如图2所示.由图2可知，每相绕组的磁链约为1.07×10-3 Wb，感应电动势有效值约为2.78 V，电动机负载时的平均转矩约为1.36 mN·m.

当电动机中输入三相电流，电动机稳定运行时，电动机的电磁转矩T表达式［7］为

T=32ΨI=93π2NlNtAwIL，（6）

式中： Ψ为电动机定子每相绕组的磁链；I为输入电流；Nl为绕组层数，为4层；Nt为绕组每层每相的匝数，为10匝；Aw為磁矢势的绝对值；L为电动机长度，为20.0 mm.

电动机感应电动势有效值表达式为

El=4.44f NΦ，（7）

式中： El为导体内部产生的感应电动势有效值；f为电动机频率；N为绕组每相的匝数；Φ为磁通量.

通过式（6）计算可得： Ψ=1.08×10-3 Wb，T=1.29 mN·m，El=2.80 V.电动机电磁性能参数理论计算值与仿真计算值比较如表1所示.

表1  电磁性能参数理论计算值与仿真计算值比较

计算方法磁链/（10-3 Wb）感应电动势有效值/ V转矩/（mN·m）

理论计算1.082.801.29

仿真计算1.072.781.36

偏差/%-0.9-0.75.4

由表1可知，所设计电动机的磁链、感应电动势有效值和转矩的理论计算值与仿真计算值的偏差分别为-0.9%、-0.7%和5.4%.偏差在合理范围内，因而电动机的仿真计算模型可以反映其电磁特性.

2  FPCB电动机损耗分析

导管泵用电动机的损耗会降低电动机效率，直接影响电动机内部温度场分布和设备运行安全，因此高速永磁电动机损耗的准确计算是电动机稳定运行的保障.对于高速电动机，定子铁芯内磁场变化频率增高，导致铁耗增加，准确计算铁耗尤为重要.并且绕组处于频率较高的交变磁场中，绕组的损耗与绕组产生的涡流损耗也是准确计算电动机温升分布的关键.

2.1  电动机铁芯损耗解析计算

铁芯损耗主要由磁滞损耗、涡流损耗和附加损耗三部分组成.铁芯损耗的计算公式［8］如下：

PFe=Ph+Pc+Pe，（8）

Ph=KhfBαm，（9）

Pc=Kcf2B2m，（10）

Pe=Kef1.5B1.5m，（11）

式中： PFe为铁芯损耗；Ph为铁芯的磁滞损耗；Pc为铁芯的涡流损耗；Pe为铁芯的附加损耗；Kh为磁滞损耗系数；Kc为涡流损耗系数；Ke为附加损耗系数；Bm为铁芯的磁通密度.

2.2  绕组涡流损耗解析计算

电动机在高速运转时，绕组暴露在交变的磁场中，使得导管泵用电动机产生绕组涡流，产生损耗.绕组的涡流损耗Peddy计算公式［4］如下：

Peddy=E2l2Rh，（12）

式中： Rh为相电阻.计算公式如下：

Rh=ρLaS，（13）

式中： ρ为电阻的电导率；La为单相绕组导线长度；S为导线的截面积.

2.3  电动机绕组铜损解析计算

绕组的铜损是导致电动机发热的主要原因.根据Joule-Lenz公式，可以得到铜损Pcu的计算公式：

Pcu=mI2Rh，（14）

式中： m是电动机的相数.

根据式（8）、（12）和（14），可以分别计算得到电动机的铁芯损耗为273.3 mW，绕组涡流损耗为151.0 mW，电动机的铜损为3 141.0 mW.

通过仿真可以得到电动机铁芯损耗、铜损及绕组涡流损耗的分布曲线（见图3），还可以得到三者的平均值，分别为238.0、2 950.0、141.7 mW.

电动机铁芯损耗、铜损及绕组涡流损耗的理论计算值与仿真计算值的对比见表2.

由表2可知，无论是理论计算值还是仿真计算值，铜损均约占总损耗的88%，是电动机发热的主要来源.因此，电动机铜损的准确计算是计算电动机温升分布的关键.

3  多物理场耦合分析

损耗作为导致电动机内部发热引起温升的主要原因，对其进行分析也成为热分析一个不可或缺的重要步骤［3］.笔者使用电磁学方法分别计算了电动机的铁芯损耗、铜损及绕组的涡流损耗，并以损耗作为热源来计算电动机各部件的温度，最后采用流场仿真方法分析了电动机在高速运转时的血液相容性.电动机温度的升高会影响电动机材料的特性，进而影响到电动机每个部件的损耗.同时，电动机温度的变化也会影响血液性质的变化，进而影响到血液的温度［9］.因此，有必要对电动机进行双向耦合仿真，以进一步提高计算精度.

在电动机多物理场的仿真计算中，双向耦合法相较于单向耦合法更符合经皮导管泵用电动机的实际运行状况［10］.本研究中所设计的微型电动机在有限空间内比普通电动机具有更高的电磁负载和热负载.准确计算电动机各部件的损耗是计算电动机温升分布的关键.

在电磁场、温度场及流场的耦合关系中，电磁场与流场之间是弱耦合关系，二者相互影响较小.而电磁场与温度场、温度场与流场之间是强耦合关系，它们之间相互影响较大.因此，对所设计的经皮导管泵用电动机进行多物理场双向耦合仿真时，仅考虑经皮导管泵用电动机电磁场与温度场、温度场与流场之间的耦合关系.耦合关系示意图如图4所示.通过多物理场间的双向耦合仿真，分析了该经皮导管泵用电动机电磁性能、各部件损耗及电动机的温度场分布情况［11］.

3.1  电磁场-温度场耦合关系分析

电动机在运行过程中伴随着能量的交换，电动机的温度直接影响到电动机的可靠性，因此必须准确计算电动机的温度.传热有3种方式，即热传导、热对流和热辐射.本研究中，热辐射换热的传热量远小于热传导和热对流换热的传热量，因此仅考虑热传导和热对流效应.根据传热理论，电动机稳定运行后的传热方程［12］可表示为

Kx2Tx2+Ky2Ty2+Kz2Tz2+q=0，

-KTnS1=0，

-KTnS2=α（T-Te），（15）

式中：T为温度；Kx、Ky和Kz分別为x、y和z轴的导热系数；q为热源密度；K为导热系数；S1为绝缘边界；S2为能量释放边界；α为S2的散热系数；Te为S2周围的温度.

3.1.1  耦合因素分析

通过瞬态场的计算，可以分别得到电动机的铁芯损耗、绕组涡流损耗和绕组铜损3种损耗.随着电动机的运行，由于3种损耗导致电动机温度不断升高.当电动机由于传导或对流散发的能量和电动机产生的损耗达到平衡时，电动机将保持恒定温度运行.然而其中的绕组铜损并非恒定值，原因是绕组的电阻率随温度升高而改变.电阻率与电动机温度关系式［11］为

ρ=ρ22［1+（t-22）］，（16）

式中： ρ为各部件的电阻率；t为电动机温度；ρ22为当电动机温度为22 ℃时的电阻率.

3.1.2  基于电磁场-温度场耦合模型的损耗和温度计算

通过对FPCB电动机电磁场-温度场耦合因素的分析，考虑到温度变化对电动机绕组材料属性的影响，在对电动机进行电磁场与温度场耦合仿真时，采用了双向耦合仿真的方法.通过对双向耦合模型的计算，得到了电动机双向耦合结果，并将该结果与未考虑温度对绕组材料影响的单向耦合结果进行对比.具体对比结果如图5与图6所示.由图5可知，随着电动机温度的升高，经皮导管泵用电动机进行电磁场-温度场双向耦合仿真后，定子铁芯的损耗均值、绕组的铜损均值和绕组的涡流损耗均值分别约为264.3、3 113.0和159.7 mW，与单向电磁场耦合结果相比，分别高了26.3、163.0和18.0 mW.

由图6可知，随着电动机运行时间的增加，电动机温度不断升高，温度的变化对电动机各部件损耗产生了较大影响.这是因为当电动机运行时，各个部件材料的特性也会发生变化，尤其是绕组材料电阻率会增大，整个导线的电阻会变大，进而绕组的铜损也会增加，使得整个电动机的温度进一步升高.电动机温度的上升会降低电动机的输出性能.因此，电动机的平均转矩从1.36 mN·m降为1.28 mN·m，影响了电动机的输出性能，降低了电动机效率.

将电动机损耗作为载荷进行温度场仿真，得到两种耦合状态下电动机温度分布云图，如图7所示.

由图7可知，在电磁场与温度场的两种耦合模型中，电动机温度最高部件均为绕组，温度分别约为89.01和95.39 ℃.稳定运行时，两种耦合模型的电动机各部件及其整体温度比较如表3所示.

由表3可知，相较单向耦合模型，双向耦合的模型中，电动机各个部件温度都有所上升，电动机的整体温度从55.80 ℃增加到58.56 ℃.这是因为温度升高会提高电动机绕组的电阻，因而整个电动机的温度也会升高，电动机温度与电动机绕组电阻之间是相互影响的.由于双向耦合仿真中考虑了温度对材料特性的影响，因此能够更加准确地计算电动机的损耗和温度.

对损耗进行双向耦合仿真计算时，只考虑了温度对绕组材料特性的影响，忽略了对其他部件材料特性的影响，后续研究中需要考虑这一点，以进一步提高温升分布计算的准确性.

3.2  温度场-流场耦合关系分析

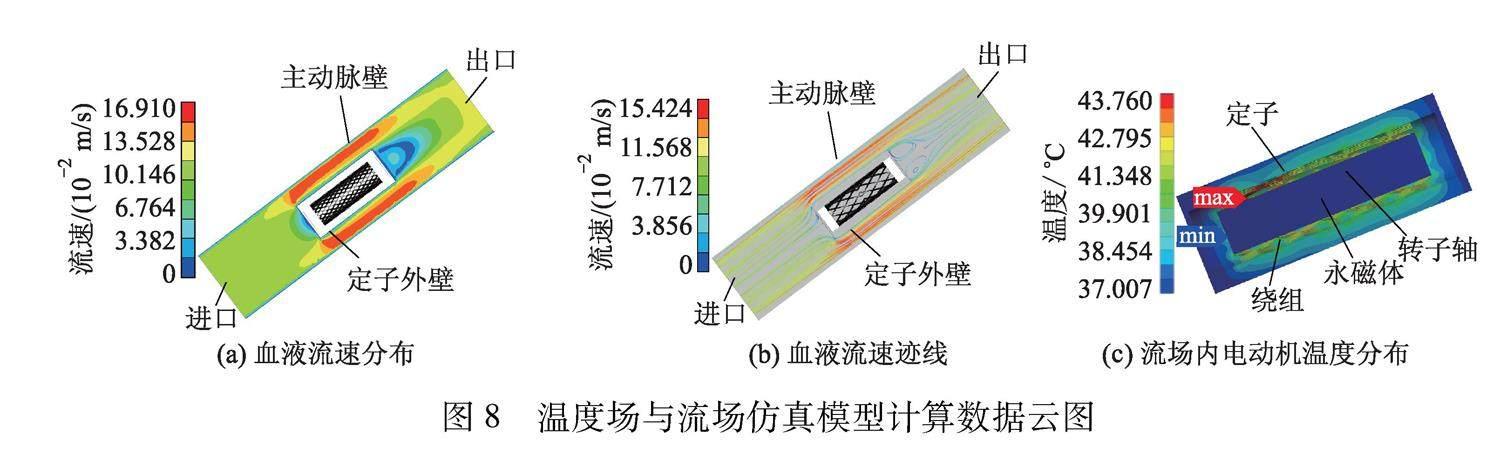
进行温度场-流场耦合仿真模型计算时，仿真模型设定条件［13］如下： ① 仿真模型选用标准k-ε模型； ② 流体材料选用水代替血液，水的进口流速设定为0.5 m/s，进口温度设定为37.00 ℃，出口压力设定为0 Pa； ③ 流固耦合交界面选择热流模式； ④ 流固耦合界面的网格选用动态网格.温度场-流场耦合仿真模型计算数据云图如图8所示.由图8可知：电动机定子外壁与主动脉壁之间的部分血液流动速度比较快，但与电动机轴向和径向部分接触的血液流速较为缓慢，这就造成了电动机与血液边界层的血液不能及时流走，电动机产生的热量就不能被血液及时带走，引起血液温度的升高（见图8a）；与电动机径向部分接触的血液在出口处会形成血液涡流现象，从而产生血栓，造成血损（见图8b）.

由图8c可知，电动机在血液中稳定运行时，其最高温度在绕组部分，约为43.76 ℃，电动机外表面温度约为37.01 ℃.这是因为绕组与电动机定子接触，两者之间热量相互传递，绕组的热量会有效地传递到电动机定子上，流动的血液又会对定子起到降温作用.当运行稳定时，定子外表面温度与血液温度趋于一致.

随着电动机的运行，由于与电动机定子接触部分的血液流速比较缓慢，接触部分血液热量不能被快速带走，温度不能有效降低，造成边界层血液温度上升.研究［9］表明，如果血液温度长期处于40.00 ℃左右，血红细胞膜的稳定性和形变能力会受到影响，抗氧能力会有所降低，影响血液相容性.为避免过高的温度影响电动机性能和血液相容性，同时为了提高导管泵用电动机的泵血能力，需要对绕组结构进行优化.

4  绕组结构的优化及损耗分析

当绕组通过电流时，且电流的每个相位与相应的感应电动势相位相同，则电动机的转矩是恒定的.根据电动机的电磁转矩公式（6），电动机的转矩常数kT可表示为

kT=32Ψ=93π2NlNtAwL.（17）

由式（13）和（17）可知：当电动机定子绕阻的长度增加时，电动机的转矩常数和相电阻会同时增加，电动机转矩常数的增加会提高电动机的性能.但是电动机相电阻的增加会增加电动机的损耗，因而无法准确评估电动机的性能.为此，定义了一个性能参数kp，即

kp=kTRh.（18）

4.1  绕组结构

研究了菱形绕组的广义形式，绕组结构如图9所示，其中变量c和d是两个还原因子，变化范围为0～1.

当改变变量c和d的大小时，电动机定子绕组形状会发生变化.因此，此时转矩常数kT一般表达式［7］为

kT=93π2NlNtAwLcπ2cos dπ2+

1-d1-c1-sin cπ2.（19）

當c=d=0时，绕组的形状为本研究中所设计的菱形绕组；当c=0.450，d=0.241时，绕组的形状为本研究中优化设计的六边形绕组.根据式（18）和（19），可以计算得到采用两种形状绕组时的电动机性能参数kp.表4为两种形状绕组电动机主要参数对比.

由表4 可知，当绕组形状由菱形变为六边形时，电动机性能参数从0.501 4增大到0.565 6，增大了约12.8%，使电动机性能得到提高.这是因为六边形绕组的整个长度相比菱形绕组变短，导致电动机电阻减小，由式（9）可知电动机的性能参数因此而增大.又由于电动机绕组暴露在交变磁场中的有效长度变长，使得电动机的转矩常数增大，提高了电动机的性能参数.可见，六边形绕组更加有利于电动机性能的提升.

4.2  优化后的电动机仿真计算验证

对菱形绕组电动机和六边形绕组电动机分别进行了仿真计算，电动机的损耗及其输出转矩的仿真结果见图10和图11.由图10可知：当绕组从菱形变为六边形结构后，电动机总损耗从3 538.2 mW降低到3 506.7 mW，降低了约31.5 mW；铜损约占总损耗的88%，它是电动机发热的主要来源.由图11可知，优化后，电动机平均输出转矩从1.36 mN·m增加到1.58 mN·m，增加了约16.2%.综上，当改变绕组形状后，电动机的总损耗降低，转矩增大，提高了电动机的输出性能.同时，电动机损耗降低后，电动机整体的温度也随之降低，满足了血液相容性要求.

5  结  论

1） 损耗计算分析中，电动机的铜损占总损耗的88%左右，是导管泵用电动机发热的主要来源，且双向耦合仿真模型更能准确地计算电动机损耗.

2） 在电磁场-温度场耦合仿真模型计算中，电动机的损耗会转变为电动机温度的升高.温度升高使得绕组的电阻变大，使得绕组温度升高，而经过热传递，又会影响到电动机整体温度的变化.因此，采用电动机电磁场-温度场双向耦合仿真计算，能够提高导管泵用电动机温度计算的准确性.

3） 在温度场-流场耦合仿真模型计算中，电动机温度升高使得血液温度升高.如果血液长期处于40.00 ℃左右的环境中，会影响到血液相容性.同时，流动的血液会带走电动机部分热量，对电动机起到降温的作用.因此，采用了温度场-流场双向耦合仿真模型，能够准确反映电动机在流场中的温度变化及其对血液温度的影响.

4） 与菱形绕组结构相比，采用六边形优化绕组结构的电动机转矩增大了约16.2%，提高了电动机输出性能，且总损耗有所降低.

[WT5HZ]参考文献（References）[WT5”BZ]

［1］  ZHUANG Y P， HOU W S， ZHENG X L， et al.A MEMS-based electronic capsule for time controlled drug delivery in the alimentary canal［J］.Sensors and Actuators A： Physical， 2011，169：211-216.

［2］  张宇娇，孙梦云，阮江军. 基于有限元法的多相异步电动机电磁场分析［J］.大电动机技术，2011（5）：24-28，34.

ZHANG Y J， SUN M Y， RUAN J J.Multi-phase asynchronous motor′s electromagnetic field analysis based on finite element method［J］.Large Electric Machine and Hydraulic Turbine， 2011（5）：24-28，34.（in Chinese）

［3］  谢颖，王泽，单雪婷，等. 基于多场量的笼型感应电动机三维瞬态磁热固耦合计算分析［J］. 中国电动机工程学报，2016，36（11）：3076-3084.

XIE Y， WANG Z，SHAN X T， et al. The calculations and analysis of 3D transient magnetic-thermal-solid coupling for squirrel-cage induction motors based on multi fields［J］. Proceedings of the CSEE， 2016，36（11）：3076-3084.（in Chinese）

［4］  孔晓光，王凤翔，邢军强. 高速永磁电动机的损耗计算与温度场分析［J］. 电工技术学报，2012，27（9）：166-173.

KONG X G， WANG F X， XING J Q. Losses calculation and temperature field analysis of high speed permanent magnet machines［J］. Journal of Electrical Engineering Technology， 2012，27（9）：166-173.（in Chinese）

［5］  TRAXLER-SAMEK G， ZICKERMANN R， SCHWERY A. Cooling airflow， losses， and temperatures in large air-cooled synchronous machines［J］. IEEE Tran-sactions on Industrial Electronics， 2010，57（1）：172-180.

［6］  MARKOVIC M，PERRIARD Y. Simplified design me-thodology for a slotless brushless DC motor［J］.IEEE Transactions on Magnetics， 2006，42（12）：3842-3846.

［7］  DEHEZ B， BAUDART F， MARKOVIC M， et al. Theoretical and experimental investigation of flex-PCB air-gap windings in slotless BLDC machines［J］. IEEE Transactions on Industry Applications， 2014，50（5）：3153-3160.

［8］  BOGLIETTI A， LAZZARI M， PASTORELLI M. A simplified method for the iron losses prediction in soft magnetic materials with arbitrary voltage supply［C］∥Proceeding of the 35th IAS Annual Meeting and World Conference on Industrial Applications of Electrical Energy. New York， USA： IEEE， 2000：269-276.

［9］  吳正洁. 温度对人红细胞及血红蛋白结构功能的影响［D］. 广州：暨南大学，2007.

［10］  TAN D， WU Y S， KUN Y， et al. A study on the electromagnetic-temperature coupled analysis method for in-wheel motors［J］.Applied Sciences， DOI：10.3390/app9204206.

［11］  CHEN Y Q， ZHOU J， FANG Y T， et al. Multi-field coupling finite-element analysis of the temperature rise in permanent magnet synchronous motor applied for high speed train［J］. International Conference on Electrical Machines and Systems，2016，135（11）：7-8.

［12］  KEFALAST D，KLADAS A G. Thermal investigation of permanent-magnet synchronous motor for aerospace applications［J］.IEEE Transactions on Industrial Electro-nics， 2014，61（8）：4404-4411.

［13］  韩雪岩，宋聪. 基于磁热耦合法车用永磁同步电机温升计算及影响因素的研究［J］. 电机与控制学报，2020，24（2）：28-35.

HAN X Y， SONG C. Research on temperature rise influen-cing factors and calculation of permanent magnet synchronous motor for vehicle based on magneto-thermal coupling method［J］. Electric Machiners and Control， 2020，24（2）：28-35.（in Chinese）

（责任编辑  赵  鸥）