桥门式起重机箱形梁截面形状和尺寸组合优化*
2024-05-29程文明
杨 益 程文明,2 饶 雄
1 西南交通大学机械工程学院 成都 610031 2 轨道交通运维技术与装备四川省重点实验室 成都 610031
0 引言
起重机主梁是桥门式起重机的主要受力部件,其承载性直接关系到起重机的安全性和可靠性,统计数据表明[1]:桥门式起重机的主梁占起重机自重的30%~60%。随着人们对保护环境的意识不断增强,国家出台了相关政策以鼓励企业降低能耗,所以工程中对箱形梁结构进行轻量化设计有着重要的研究意义。
到目前为止,国内外学者对桥门式起重机轻量化进行了大量研究。朱强等[2]基于SIMP变密度法与数学折中规划优化法,建立了桥式起重机多工况优化模型,通过Optistruct求解器以体积分数和静态位移为约束,在3种典型静态工况下以最小柔度为目标进行多工况拓扑优化,优化后的主梁质量减轻6.055%;Abid M等[3]在综合考虑加劲肋的形状、尺寸、位置及箱形梁截面等参数的基础上,采用2部优化策略对起重机箱形梁结构的轻量化进行研究,通过优化箱形梁结构的宽度、高度和厚度尺寸可得到合理的减重方案;宋佳雄等[4]为得到合理的起重机主梁结构建立以主梁截面尺寸和构件厚度为设计变量,综合考虑主梁结构强度、刚度约束条件,并以主梁质量最小为目标函数的数学模型,采用Ansys软件中的零阶优化算法求解该模型,优化后主梁结构质量可缩减23.1%;付为刚等[5]以竹子为仿生对象对正轨箱形梁横向肋进行结构优化,并建立了正轨箱形梁加劲肋变间距等稳定性优化策略,结合有限元弹性屈曲分析进行迭代优化,实现了加劲肋变间距等稳定性设计,最终仿生箱形梁较传统箱梁减重136.12 kg,各截面屈曲抗失稳能力差异减小;王玉璞等[6]以粒突箱鲀鱼嘴特征曲线为仿生原型,设计出可附着在箱形梁迎风面上的部件,并运用计算流体力学对仿生设计进行评估,研究显示以某40 t集装箱起重机箱形梁为例,仿生箱梁较传统箱形梁结构风阻减小了65.77%,增重2.28%,提高了起重机在风场重运行的平稳性。
综上所述,箱形梁结构的轻量化研究多集于利用变密度法对主梁结构进行拓扑优化、利用生物仿生设计对箱形梁的横向肋结构进行优化、对箱形梁结构中的部分零件进行尺寸优化。总之,对起重机箱形梁结构轻量化的研究主要集中在拓扑优化、尺寸优化和仿生学设计3个方向,这3种方法多局限于现有的四边形主梁截面形状,缺少对主梁截面形状的研究。
本文提出的主梁截面优化流程为:1)建立待优化主梁简化模型;2)根据轻量化目标确定形状优化和尺寸优化的组合设计变量;3)对设计变量进行灵敏度分析,并确定设计变量的变化范围;4)以自重最小为目标,以挠度为约束条件,求出箱形梁截面形状的最优解,利用该流程获得新的轻量化箱形梁截面形状。
1 40 t集装箱门式起重机参数
以某MG40 t-40 m起重机的主梁为研究对象开展主梁截面形状的优化研究,主梁结构参数如图1所示,具体参数有:上下盖板材料为Q235,板的厚度均为14 mm,腹板选用Q235,厚度为8 mm,主梁高度为2 428 mm,主梁宽度为1 518 mm,翼缘板厚度为22 mm。根据设计说明书选取MG40 t-40 m起重机最具代表性的4个工况进行静力分析,具体工况如表1和表2所示。
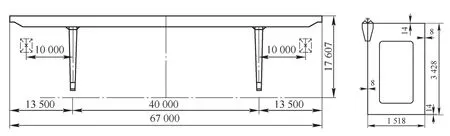
图1 32 t门式起重机示意图

表1 4个工况中主梁、起重小车的状态和位置
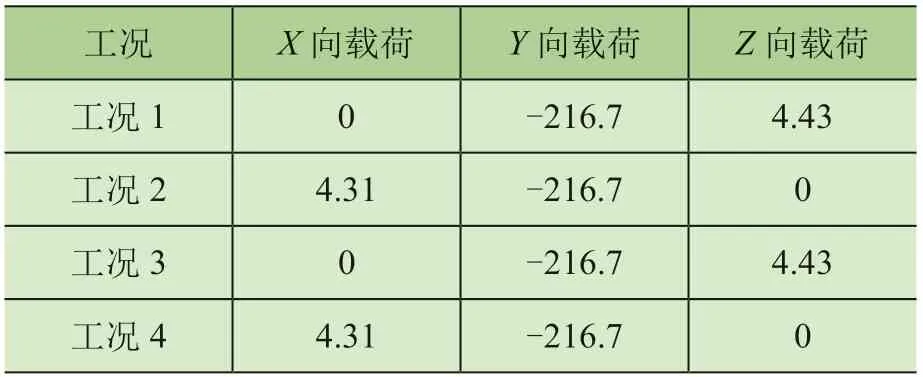
表2 4个工况载荷参数 kN
2 尺寸和形状优化及结果分析
2.1 主梁有限元模型
主梁模型截面高度为2 414 mm,宽度为1 628 mm,长度为62 787 mm,单元类型为Shell 63壳单元,用四边形结构化网格划分,单元数量为52 860,节点数量为82 720。材料的弹性模量为E=2.1×105MPa,泊松比为μ=0.3,密度为ρ=7.85×10-9t/mm3。
本文仅研究截面形状对主梁的影响,所以模型排除主梁内部隔板、翼缘板等改善局部应力的结构[7],同时为降低载荷区域的应力集中现象,将载荷区域多个节点通过柔性节点REB3共结在一起进行加载,分别施加在箱形梁有效悬臂位置和箱形梁跨中位置。载荷位置和节点分布如图2和图3所示。

图2 主梁载荷施加位置

图3 REB3节点示意图
2.2 形状优化设计变量а的定义
形状优化[8,9]是采用节点法思路将截面形状用若干个节点划分成若干线段,并通过控制节点间网格的位移来对网格进行形状的变化。通常将节点变形前的空间位置称作初始位置,记作X0;将1个节点的最大位移距离看作1个一维常向量统称为节点位移向量,记作ΔXj,如图4中变形起点和终点之间的箭头所示。

图4 形状优化的设计变量
为了便于计算,在优化过程中ΔXj保持不变,算法只对ΔXj按一定缩放系数进行变化,且缩放系数是一个标量,取值范围为[-1,1],其中1表示节点可移动ΔXj数值上的最远处,-1表示节点可移动ΔXj数值上的反向最远处,故形状优化中的设计变量确定为缩放系数а。
通过优化后的节点位置称为终点位置,记作X,故形状优化的通用数学模型可表示为
其中
将主梁截面按图5所示的22个节点分成22段,再按图6所示将节点划分为10对节点变形组,这10对节点的初始位置记作初始位置X0,即
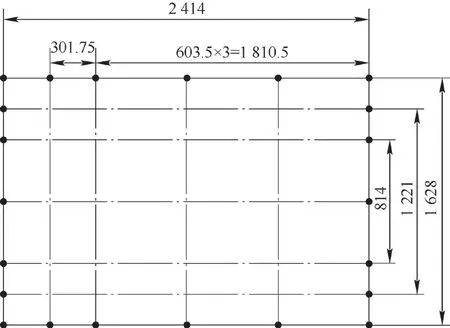
图5 节点的分布位置
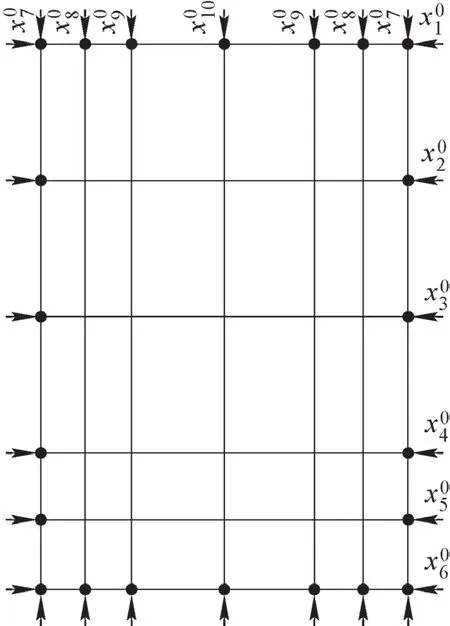
图6 节点初始位置X 0
形状优化的设计变量а对应的X0为
其中,а1、а2、а3、а4、а5、а6通过控制对应的节点水平移动从而引导截面宽度方向变形;а7、а8、а9、а10控制对应的对节点竖直位移引导截面高度方向变形。
2.3 尺寸优化设计变量Ti的定义
箱形梁的主要受力零件是上盖板、下盖板和腹板,将这些板材的板厚作为设计变量Ti,即上盖板板厚Ta、腹板板厚Tp、下盖板板厚Tb,如图7所示。设计变量与尺寸之间的线性关系可表示为
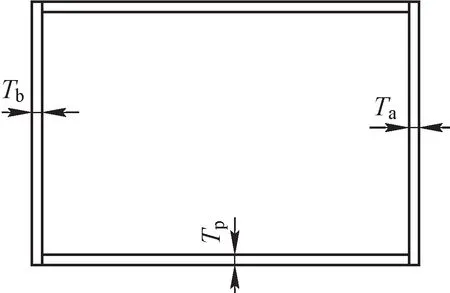
图7 尺寸优化设计变量
式中:p为属性中要优化的对象,C0为常数,Ti为设计变量,Ci为每个设计变量变化的线性系数。
由于优化对象为壳单元的厚度,即C0=1,Ca=Cp=Cb=1,故式(2)可简化为
2.4 设计变量灵敏度分析
灵敏度分析[10]是结构优化中常用的手段,常用于寻找结构性能影响最大的设计变量。设计变量变化的灵敏度数值直观地反映了该变量对性能的影响程度和趋势,故可用于快速筛选出重要的设计变量进行优化。
灵敏度分析一般是用于分析系统输出响应对系统输入参数的敏感度,对复杂的数学模型求取其倒数的阶数较高时较复杂,鉴于此,常规的灵敏度分析均为设计响应对设计变量的一阶偏导数,其数学表达式为
式中:g(X)为系统性能指标,X为系统设计参数向量,xi为系统设计参数向量中的第i个参数。
箱形梁截面形状和尺寸优化的设计变量关于质量、挠度的灵敏度分析结果如图8、图9所示。由图8可知,为减轻主梁自重应减小а1、а6、а7等3个变量数值;由图9可知,提高变量а2、а3、а6、а8的数值可降低主梁的挠度。
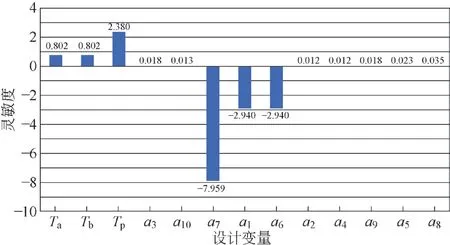
图8 设计变量关于主梁质量的灵敏度
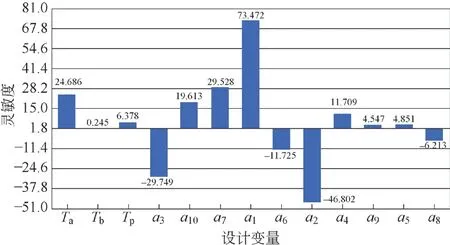
图9 设计变量关于主梁挠度的灵敏度
经分析,减小设计变量а1、а6、а7数值对减重有利,增加这3个设计变量数值对降低挠度有利,故在优化时需给予这些设计变量足够的变化空间求解出最优解。
2.5 优化的数学模型
本文优化的目标是箱形梁质量最轻。根据灵敏度分析结果和箱形梁结构模型参数,以及板厚初始值,设计变量板厚Ti变化范围,如表3所示。节点初始位置X0的初始值、节点位移向量ΔXj的距离、缩放系数а的变化范围如表4所示。
表3 板厚初始值和变化范围Ti
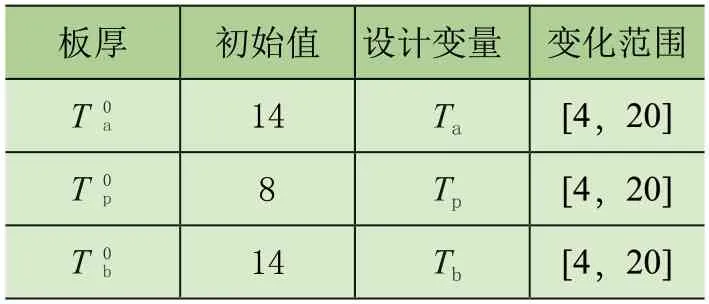
表3 板厚初始值和变化范围Ti
板厚初始值设计变量变化范围T0 a 14 Ta[4,20]T0 p 8 Tp[4,20]T0 b 14 Tb[4,20]

表4 初始位置X0、变形向量ΔXj、缩放系数a
优化约束条件为根据设计书工况1、工况2中跨中位置的Y向位移约束边界为Cmid≤-40 mm;工况3、工况4中悬臂位置的Y向位移约束边界为Cleft≤-28.6 mm。形状优化和尺寸优化的数学模型可表示为
3 优化结果分析
3.1 主梁截面形状与质量的耦合关系
经过18次迭代运算后,得到主梁自重最轻的截面形状,以及主梁截面形状与质量耦合关系曲线,如图10、图11所示。
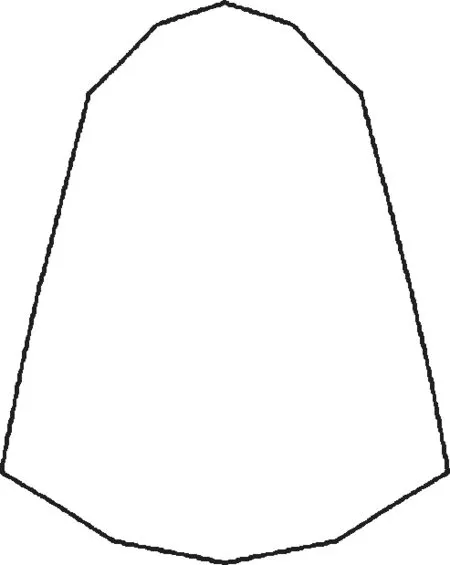
图10 主梁截面形状优化的最优解
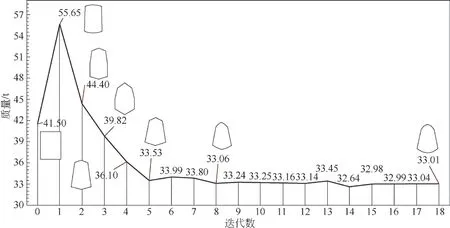
图11 主梁截面形状与质量耦合关系曲线
由图11可知,计算过程中的主梁自重随迭代次数的增加逐渐趋于收敛,故该优化结果有效。优化前四边形主梁自重为41.5 t,优化后的箱形梁截面形状由四边形变成多边形,且自重降至33.01 t,减重20.46%。
通过分析图11形状变化规律,可知迭代数0、1、2、3、4、5、8、18的形状发生标志性变化,将这8个标志性形状后对应的设计变量Xi、Ti的优化结果单独列表,如表5所示。
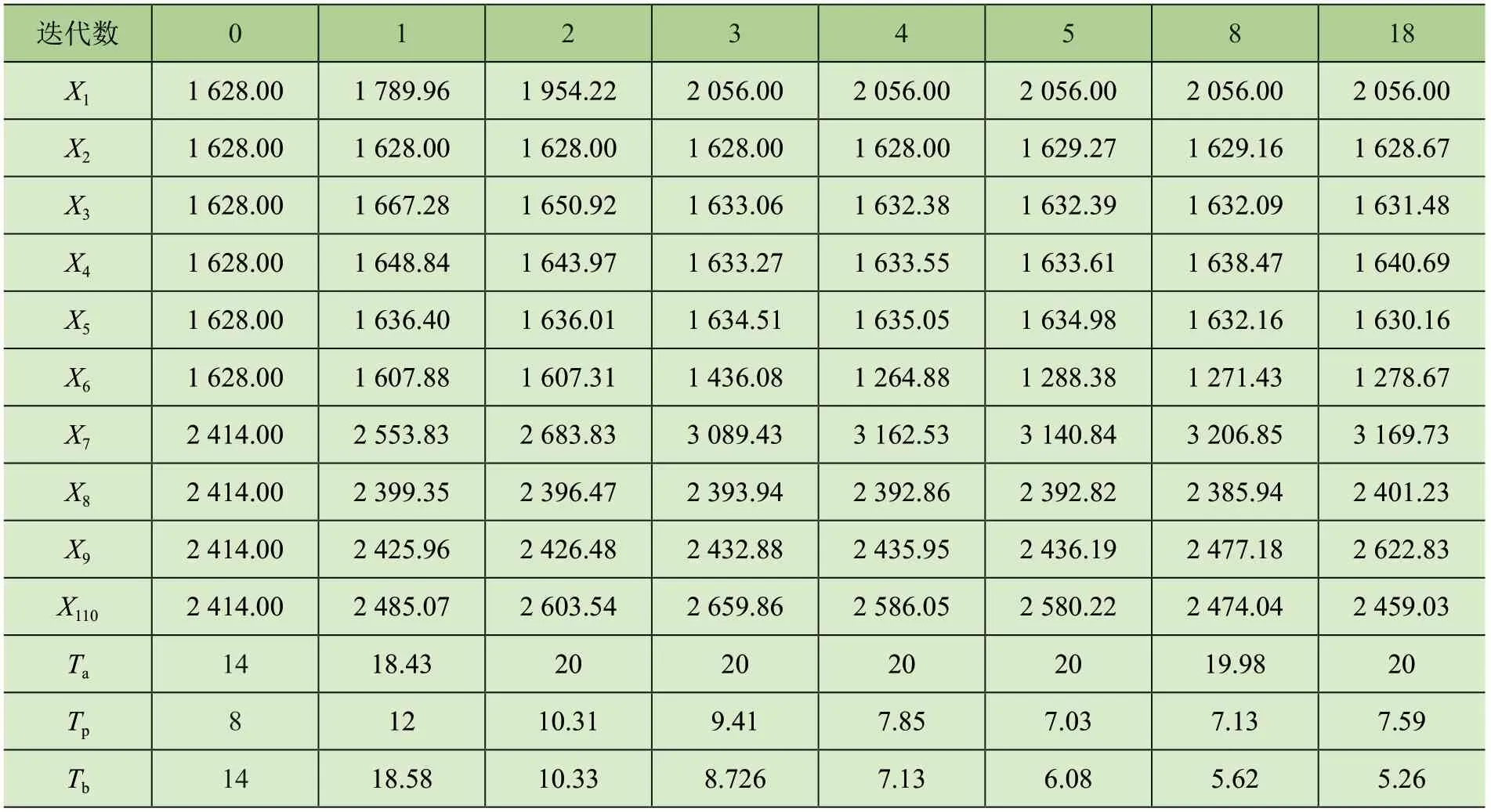
表5 8个标志性主梁截面形状和尺寸优化设计变量的值
3.2 优化后主梁结构的静力和线性屈曲分析
结构屈曲分析能够用去确定结构开始变得不稳定是的临界载荷,也能从侧面反映出主梁结构受力时的临界载荷。故对新的主梁结构进行静力和屈曲分析。通过静力分析后,获得优化前后各工况的最大位移、最大应力如表6所示。通过线性屈曲分析可以得出箱形梁结构在工况2和工况4的载荷条件下的屈曲特征值λi数值如表6所示。屈曲临界载荷Fi的计算公式为
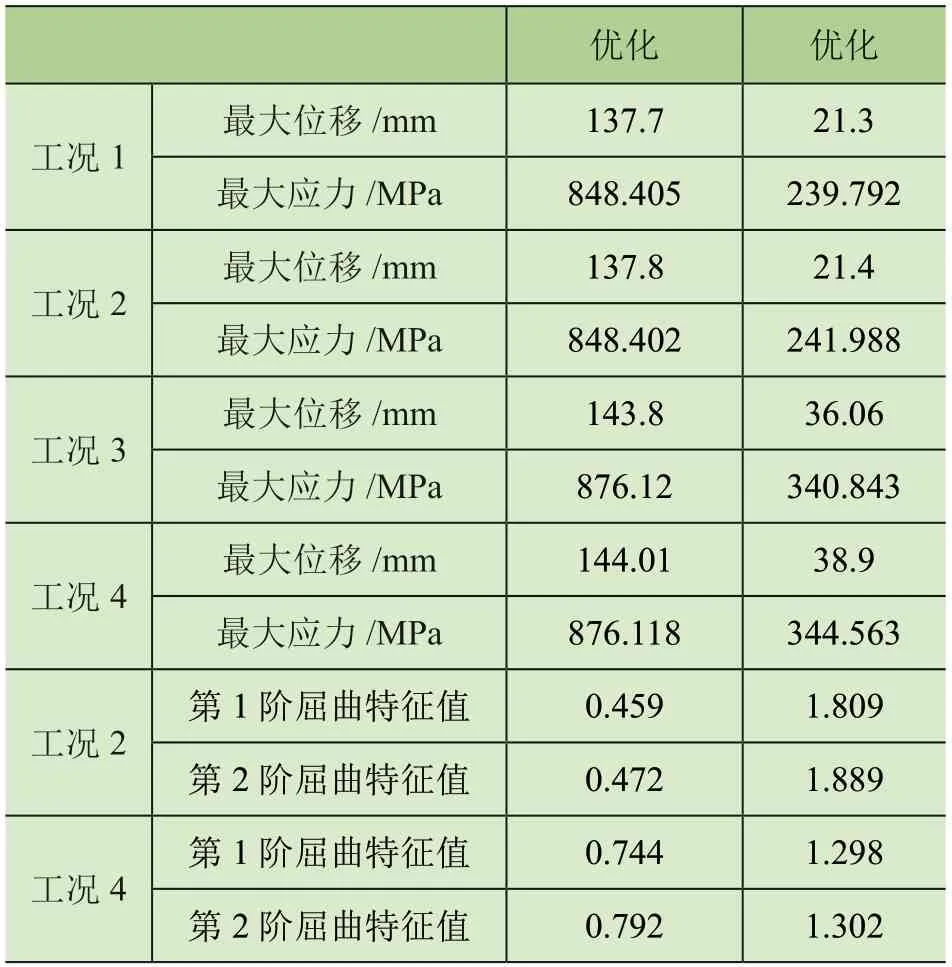
表6 优化前后各工况的位移、应力、屈曲特征值
式中:Fi为第i阶屈曲临界载荷,λi为第i阶屈曲特征值,Wn为第n个工况的载荷。
由表6可知,优化后的箱形梁结构在4种工况中的最大位移和最大应力均大幅低于优化前结构,其中最大位移降低84.53%,最大应力降低71.74%。
分别将工况2、工况4优化前后的Wn、λi代入式(6)得到优化前后第1阶、第2阶的屈曲临界载荷如表7所示。由表7可知,主梁结构经优化后在工况2、工况4的前2阶屈曲临界载荷均高于优化前,且比原结构最大高出300%。
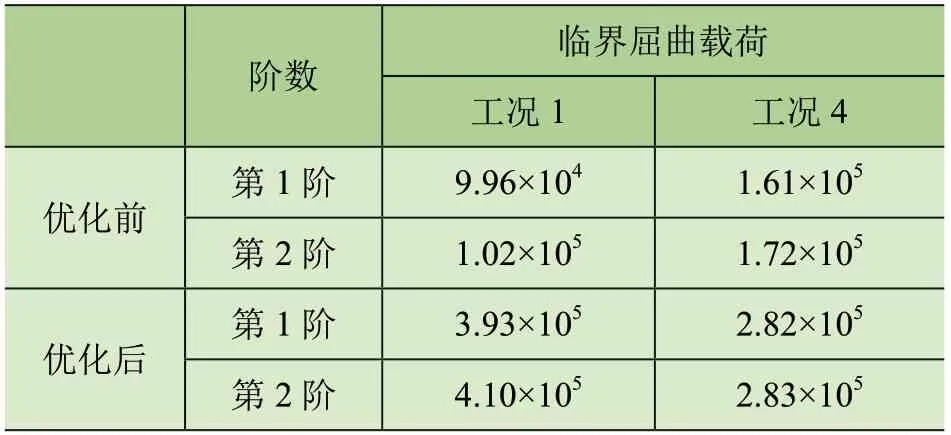
表7 优化前后第1阶、第2阶临界屈曲载荷 N
4 结论
本文通过对门式起重机主梁截面的优化,实现了箱形梁结构的轻量化设计。利用形状和尺寸优化组合的优化模型,对箱形梁结构进行轻量化求解,经18次迭代后得到新多边形的主梁结构。对新结构进行静力和线性屈曲分析得到以下结论:
1)箱形梁截面经过形状和尺寸优化后,得到新的截面形状和上下盖板,2腹板的板厚,新的多边形主梁结构减重20.46%;
2)新箱形梁结构的最大位移和最大应力均大幅低于优化前原箱形梁结构,最多下降70%;
3)新箱形梁结构第1阶、第2阶的临界屈曲载荷均高于优化前结构,且高出3倍。
