智慧追问助力思维发展,培养数学核心素养
2024-05-29王瑞
王瑞
[摘 要] 在小学数学课堂教学中,追问是提升学生思维品质的“金钥匙”。教师可以基于知识的衔接处智慧追问,磨砺思维的深刻性;基于知识的关键处智慧追问,磨砺思维的批判性;基于思维的浅表处智慧追问,磨砺思维的广阔性;基于学习的疑问处智慧追问,磨砺思维的严密性;基于课堂的总结处智慧追问,磨砺思维的概括性。
[关键词] 追问;数学思维;数学核心素养
追问作为一种提问的技巧,是在提问基础上的延伸与拓展,可以深化学生对知识的理解与认识,可以促进探究性学习的开展,可以促进理性思维的深入。追问是一种有效的教学引导方法,在数学教学中有着广泛的应用。小学数学课堂教学经历了从“两基”到“三维”再到“核心素养”的嬗变,对教师课堂教学提出了更高的要求。在教学过程中,教师要从数学学科特质出发,在提问处智慧追问,引导学生触及知识本源,开展高效的数学学习活动,更好地助力学生思维的发展和培养核心素养。
一、基于知识的衔接处智慧追问,磨砺思维的深刻性
从数学知识的整体架构上看,教学内容在編排上有较强的关联性,知识点的呈现也是层层递进的。因此,在课堂教学中,教师要站在一个较高的视角从知识间的关联性出发,从教学内容的逻辑结构着手合理设计教学,并找准知识同化与顺应的关键点,于新旧知识的衔接处智慧追问,打破学生的认知平衡,促使学生由此及彼地深入思考,磨砺其思维的深刻性,从而化未知为已知,促进知识、方法的迁移。
案例1 射线、直线和角
师:同学们,你们认识这个图形吗?(教师指着提前板书的一条曲线)
生1:这是一条波浪线。
生2:这是一条曲线。
师:那你们会画直线吗?请试着在纸上画出一条直线,请一名同学到黑板上来画一画。(有学生自告奋勇上台板演,其余学生则在纸上动手尝试)
师:通过刚才画直线的操作,你们有什么想法?
师:黑板上那条弯弯曲曲的线是曲线,而刚才我们画出的这些直直的线是直线。
师:让老师来量一量刚才这位同学画的“直线”,从这一端到那一端的长度是53厘米,那画出的是直线吗?(学生顿时面面相觑,片刻后学生有了想法)
生3:这是一条线段。
师:为什么?刚才你们不是认为这是一条直线吗?
生4:我们刚才在纸上画出的线都有固定长度,且有两个端点,所以是线段。
师:那你现在觉得直线是什么样的?大胆猜一猜,说一说。
生5:我觉得直线应该是永远无法画完的。
生6:我觉得直线是无法量出长度的。
生7:直线是没有端点的。
……
师:你们真厉害,一下说出直线的这么多特点,那就让我们再试着画一画吧!
小学生以形象思维为主,他们对数学知识的认知不是依靠死记硬背得来的,而是要通过“做数学”的过程不断感悟和体验生成的。当然,“做数学”的过程并非只是简单的动手操作,而是多感官协同活动的生命实践活动。基于这个视角,上述案例中教师在课始抛出一个简单的数学问题,让学生自由地画直线,并以智慧追问让学生很快否定了自己,从而引入探究直线的画法。在整个教学过程中,正是由于教师在新旧知识的衔接处适切追问,使得学生大显身手深入思考,将对知识的理解、思考、操作、探究、验证、反思、建构等过程统一起来,最终突破知识难点,提升整体思维能力。
二、基于知识的关键处智慧追问,磨砺思维的批判性
对于数学课堂教学而言,教师要在开展教学之前深入研究教材,清楚理解教材的编写意图,为后续教学目标的定位和知识重难点的把握奠定基础。学生掌握和理解知识是一个循序渐进和不断吸收的过程,这就需要教师从知识的关键处提出问题和智慧追问,以达到重点突出和分散难点的教学目的。唯有如此,才能让学生经历思维逐渐开掘的过程,实现对数学本质的理解和掌握,培养思维的批判性,让学生的数学学习逐渐走向深入,从感性走向理性。
案例2 平均数
师:首先,让我们一起来观看小小篮球队员的投篮挑战赛。(课件呈现小东的3次投篮情况:每次都投中5个;小林的3次投篮情况:分别投中3个、5个、4个。)
师:倘若我们用数字“5”来表示小东的1分钟投篮水平,那该用数字多少来表示小林的1分钟投篮水平呢?为什么?(学生陷入沉思)
生1:我觉得可以用数字“5”表示,因为他第2次投中了5个。
生2:小东3次都是投中5个才用数字“5”表示,小林只有1次投中了5个,用数字“5”表示无形中提高了他的实际水平,表示两人的水平一样了,显然对小东是不公平的。
师:那你认为用哪个数学表示更好呢?
生2:我觉得可以用数字“4”表示。
师:可小林毕竟也有1次投中了5个,用“4”表示小林会不会有意见呢?下面请同桌两人一组讨论,说一说你的想法,然后全班展示。(学生进行了热烈讨论,最后全班交流)
生3:肯定不能只看一次投中的个数,虽然3次中有1次投中了5个,比4多1;但也有1次投中了3个,比4少1。
生4:大家看,3,4,5这三个数,4刚好是中间的位置,既然用“5”表示提高了他的水平,而用“3”表示又降低了他的水平,4不是刚刚好吗?
师:非常好,这就是移多补少法,我们可以在条形统计图上试着移一移。(学生动手尝试)
师:我们再一起来看小红的3次投篮情况:分别投中3个、7个、2个。你们能找出一个数字来表示小红的1分钟投篮水平吗?(学生自主自发地采用移多补少法探寻结果,很快寻得了数字“4”)
师:有没有同学采用其他方法?(学生面面相觑)
师(启发):我们是不是可以试一试计算的方法,比如先求和后均分?(学生尝试)
师:你们觉得哪一种方法更好?(学生阐述自己喜欢的方法)
师:事实上无论是哪一种方法,都是为了让原本不相同的几个数变得同样多,这就是平均数。(板书课题)
“平均数”是虚拟的,因此是教学的一大难点。在以上案例中,教师用一个学生喜闻乐见的情境激发了学生的兴趣,在一次又一次的追问中引导学生探明知识源头,厘清知识误区,突破思维障碍,让学生通过操作、思考、探讨,将感性与理性、主观与客观等融合起来,触摸到知识的内核,让数学课堂诞生无法预约的精彩。
三、基于思维的浅表处智慧追问,磨砺思维的广阔性
数学学科是思维的学科。在实际课堂教学中,小学生对知识的理解往往比较片面,思维呈现表层化。这时需要教师透过现象看本质,用智慧的追问去引导和点拨,有意识地给学生提供科学的思维方法,搭建思维的跳板,使学生开拓思维和实现更高层次的深入思考,有效培养其思维的广阔性,发展其数学核心素养。
案例3 长方形和正方形的周长
问题:从一张长为15厘米、宽为10厘米的长方形纸中剪去一个最大的正方形,试求出剩余长方形的周长。
师:谁能说一说解决这个问题的关键点是什么?
生1:剪下的最大的正方形的边长就是这个长方形的宽,即10厘米,经过计算就可以得出剩下长方形的长与宽。
师:非常好,下面请大家试着解答本题。(学生自主解题,教师巡视)
师:看来大家都能解决本题,有没有同学发现更简便的方法?(学生陷入沉思)
生2:剩余的长方形的周长,比原长方形短了“宽×2”。
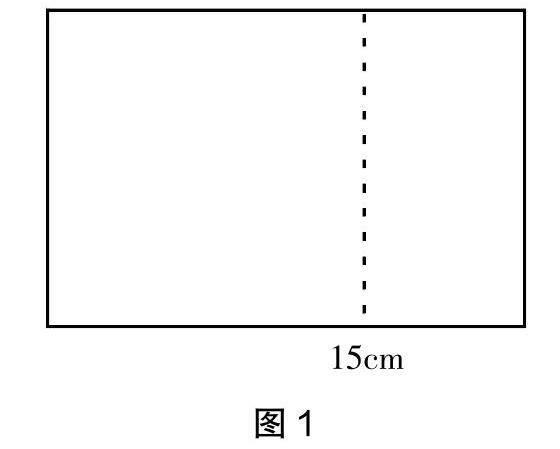
师:非常棒的思路!我们再来看这样一个问题:如图1,若从一个长为15厘米的长方形中剪去一个最大的正方形,试求出剩余长方形的周长。(学生再一次开展深入思考)
生3:剪下的最大的正方形的边长是原长方形的宽,也是剩余长方形的长。剩余长方形的长加上剩余长方形的宽即为原长方形的长,从而得出剩余长方形的周长即为原长方形长的2倍,即15×2=30(厘米)。
对于数学教学而言,解题并非终极目标,培养学生思维才是终极目标。以上案例中,教师追问于学生思维的浅表处,用问题“有没有同学发现更简便的方法”将学生的思维引向深处,让学生在深入思考与探究中发现更加丰富和广阔的认知,最终深化了理解,升华了认知,拓展了思维。
四、基于学习的疑问处智慧追问,磨砺思维的严密性
每个学生都是独特的个体,他们有着不同的思考角度,会生成各种各样的困惑和疑问。这就需要教师鼓励学生多方位、多角度去思考问题,引领学生积极发表自己独特的见解,以追问引导学生产生矛盾冲突,最终在辨析中化解认知困惑。学生在探讨中厘清知识本质,在探究中找到“发现”的快感和体验顿悟的乐趣,能极好地磨砺思维的严密性。
案例4 分数的初步认识
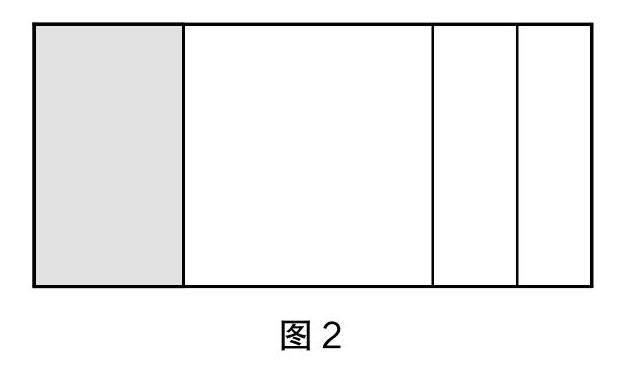
师:如图2,阴影部分是不是大长方形的??
师:经过刚才的独立思考,你们一定有了自己的想法,下面请说一說你们的结论。
生1:我觉得不是,图2中的长方形尽管被分成了4份,但并没有平均分。
师:其余同学认为呢?(大部分学生点头表示赞同)
生2:我有不同看法,尽管没有平均分,但经过仔细观察,我觉得阴影部分应该是大长方形的?。
师:现在有了两种不同观点,哪一种正确呢?
生3:我们就这样光看肯定是无法判断谁对谁错的。
生4:我们需要验证一下。
师:下面就借助桌子上的学具进行验证。
生5:我将这个大长方形分成4份,而其中的1份刚好是阴影部分的大小。
师:那其余3份呢?是不是每1份都是长方形的??
……
对于解决“用几分之一表示阴影部分”这类问题,不少学生还会因概念本身而将“平均分”作为判断依据。事实上,概念中所呈现的“平均分”本质上指的是部分与整体间的等分关系,而并非呈现在图形表面的“平均分”。在以上案例中,教师针对这一教学难点抛出问题,并针对学生学习的疑问之处开展智慧追问,让学生在判断中思辨,在思辨中明晰,最终完成对概念本质的意义建构,培养了学生思维的严密性,发展了学生高阶思维能力。
五、于课堂的总结处智慧追问,磨砺思维的概括性
教师在课堂总结时智慧追问,不仅可以为学生提供一个充分展现和自我发展的空间,让其头脑中已有认知结构更完善,还可以培养其探究精神,让其享受创造的成功感,更重要的是可以拓展其思维空间和磨砺其思维的概括性。
案例5 认识乘法
问题1:通过本节课的学习,你收获了什么?
问题2:你知道乘法是怎么产生的吗?
问题3:既然加法我们已经非常熟悉了,为什么还需要学习乘法呢?
问题4:从你身边的事物出发,列举一个乘法计算的实例。
在课堂总结处不断追问是助力学生思维不断进阶的有效策略。以上案例中,教师通过这样拾级而上的追问,为学生搭建一个充分发展思维的平台,深层次地引导学生通过联系、分析、归纳、提炼、概括,厘清知识来龙去脉,最终使知识与方法升华为数学思想,达到了事半功倍的教学效果。
总之,适时提问是优化课堂教学的催化剂,而智慧追问则是其中的点睛之笔。作为一名智慧型的数学教师,不仅要关注精心预设,还要注重利用追问抓住时机启迪学生,为学生思维的发展铺路搭桥,引发学生更创新、更深入、更全面的思考,致力“授之以渔”,发展学生的数学核心素养。
