核心素养背景下培养学生运算能力的措施研究
2024-05-29杨世成
杨世成


[摘 要] 小学生运算能力弱的主要原因有:教师忽视运算教学的重要性、学生自身能力不足、电子产品替代人工运算等。基于培养学生核心素养的背景,研究者提出培养学生运算能力的教学策略:依托生活实际,感悟算理;借助实践操作,理解算理;利用数学思想,突出算理;巧用错误资源,夯实算理。
[关键词] 运算;核心素养;教学策略
运算能力反映了学生的思维发展情况,随着信息技术的飞速发展,电子设备成为人们生活中的常规物品,各种运算也逐渐被电子设备替代,这会对学生的运算能力发展产生一些负面影响。教师应深刻认识这一点,在数学教学中加强对学生运算能力的培养,通过各种教学手段引导学生更好地掌握算理算法,提高运算的准确率,发展数学核心素养。
一、小学生运算能力弱的原因分析
1. 教师忽视运算教学的重要性
部分教师对运算教学的重视程度不够,教学过程中忽视对学生运算能力的培养。事实上,运算是促进学生逻辑思维发展的重要途径,教师应对此有一个清醒的认识,重视培养学生运算能力,进而循序渐进地提升其核心素养。教师作为教学的主导者,应革新自己的理念,对运算教学产生足够的重视,引导学生不仅关注运算结果,还要关心运算过程,感知运算带来的乐趣。
2. 学生自身能力不足
受身心发展规律的制约,小学各个年龄阶段的学生认知都有自己的特点。整体来说学生心智尚不成熟,对运算的认识比较片面,有些学生认为只要掌握基本的计算方法和获得正确结论即可。殊不知,学生缺乏对算理过程的理解,会导致各种计算错误的发生。实践证明,运算能力考验的是学生对算理的理解程度,考查的是学生的耐心。
3. 电子产品替代人工运算
随着时代的发展与科技的进步,电子产品成为人们生活中不可或缺的一部分,不论是在学习、工作还是生活中,电子产品确实给人们带来了很多便利。因为随时随地都有电子产品的辅助,这让部分学生觉得运算能力不那么重要,这种认识会导致他们运算意识淡薄,运算能力逐渐下降。
二、培养运算能力的措施
1. 依托生活实际,感悟算理
每一个学生都不是“空着脑袋”进入课堂的,学生在生活中都会积累一些与数学相关的经验。教师可将学生认知中与数学相关的生活经验挖掘出来,并将这些经验“数学化”,让学生探寻到思维的着陆点。教师可设计一些生活化的情境,带领学生从自身已有的经验出发主动发现并提出问题,同时结合自身已有的知识基础与认知水平来解决问题,成功架起学生生活与算理算法之间的桥梁,促使学生对运算做到“知其然且知其所以然”。
案例1 “小數加、减法”的教学
情境:小明将每个月的零花钱存到储蓄罐中,已知一月份存了13.5元,二月份存了6.3元,请结合表1提出与数学相关的问题。
生1:小明一、二月份一共存了多少钱?
生2:小明二月份比一月份少存多少钱?
生3:一、二月份所存的钱,可列式为13.5+6.3;二月份比一月份少存的钱,可列式为13.5-6.3。
师:非常好!这两个式子怎么计算呢?
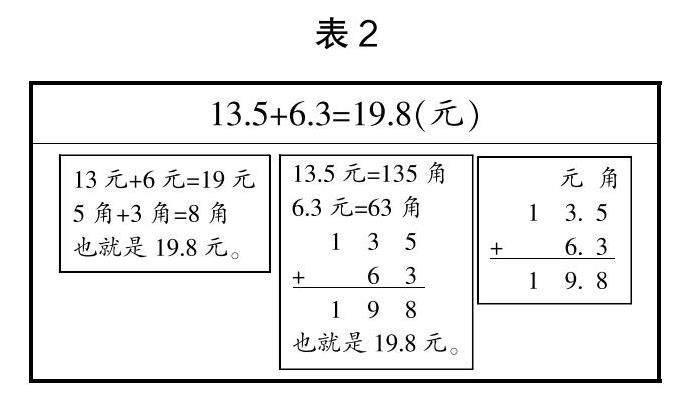
学生在讨论过程中呈现出以下几种计算方法,见表2与表3。
从学生的计算方法来看,都结合了他们的生活经验,从元、角、分的角度去分析并计算,整个计算过程反映了学生的思维过程,自然地揭示了为什么要将小数点对齐的原理。从本例来看,分别以元、角、分为单位的情况下,只有将相同单位的数字对齐才能让计算具有实际意义。通过计算方法的对比,同时结合整数加减法与小数加减法间的联系,能让学生明确小数点对齐的本质就是相同数位的对齐。此过程将生活与数学联系起来,实现了知识的迁移。
实践证明,为学生创设丰富的生活情境可将生活实际问题转化成运算问题,这是赋予运算实际意义的过程,让枯燥的计算过程变得丰富有趣;同时,学生结合自身已有的生活经验来发现问题、提出问题、分析问题、解决问题(简称“四能”),能进一步理解计算的原理,发展数学运算素养。
2. 借助实践操作,理解算理
学习应是一个生动活泼、主动且富有个性的过程,学生在课堂中听讲、思考、操作、交流等都是重要的数学学习方式。教师应为学生提供充足的时间与空间,让学生在实践操作中亲历操作、观察、猜想、计算、验证与推理等。实践发现,实践操作可将一些抽象难以理解的数学知识变得形象、具体,这是学生丰富表象的过程,能让学生在实践与观察中获得直接经验与直观体验。
关于计算教学,教师可结合教学内容特点进行设计,引导学生在实际操作中用耳朵听、眼睛看等,多感官参与活动过程,让学生从更高的视角去理解问题,对知识形成丰富完整的理解,从而掌握知识本质规律,对算理与算法形成清晰、准确的认识。
案例2 “有余数的除法”的教学
为了让学生直观地认识余数,感知余数与除数之间存在的联系,笔者在本节课带领学生用小棒来搭建小正方形:搭建一个正方形需要用4根小棒,那么13,14,15…20根小棒分别能搭出几个正方形?搭完后剩几根?
以小组合作学习的方式开展活动,学生边搭图形边填写表格(结论见表4),然后让学生通过对表格的观察谈一些思考与感悟。
学生自主操作、填表,发现小棒正好用完的情况下,不存在余数;小棒有剩余的情况下,存在余数;随着小棒数量的变化,余下小棒的数量也随之发生改变;当余数的数量达到一定程度时,又不存在余数了。两个周期之后所有学生对“余数”产生了直观形象的认识,并提炼出“余数必然小于除数”的结论。
学生经历了“实践—思考—交流—归纳”的过程,不仅自主提炼出余数与除数间的关系,还进一步训练了数学思维,积累了活动经验,为后续研究其他数学问题奠定了方法基础。实践证明,借助实物操作进行计算教学是促使学生获得直接体验的最佳方式,能让学生在自主操作过程中形成的体验与感悟,这对他们理解算理、算法具有重要意义。
此环节,在教师有效引导下,学生通过自主操作、填表、思考、总结,将实践操作与计算有机地结合在一起,亲历知识的形成过程,能够强化对算理、算法的掌握,提升运算能力。
3. 利用数学思想,突出算理
数形结合思想是最基本数学思想方法,正如华罗庚所言:“数形结合百般好,隔离分家万事休。”小学数学计算中的很多算理让学生难以理解,若借助数形结合思想和相应的描述,则能够将学生难以理解的算理变得直观易理解。在教学中,教师可以用点子图、方格图、线段图、面积模型等促使学生形成丰富的直观想象,从而理解算理,形成算法。
数形结合思想的应用让抽象的算理可见、可感,让学生在清晰的状态下拓展思维,在观察与思考中提炼、总结算法,促使深度学习的发生。
案例3 “两位数乘两位数的竖式笔算”的教学
如图1,通过点子图协助学生理解每一步竖式的意义,以14×12为例,其教学难点在于带领学生理解竖式中第二步所获得的积“14”所摆放的位置。从点子图上来看,该式的第二步本质为14×10,因此其实际意义为140,那么它的位置应对应于十位,点子图上将竖式每一步的算理都展现得淋漓尽致。
案例4 “分数乘分数”的教学
教师可以借助面积模型来分析计算过程,让学生明确算理与算法。如图2所示,分成的总份数实则为分母相乘的积,而重复阴影部分则为分子与分母相乘的积。从直观模型中,不仅能让学生明晰探索方法,还能促使学生从深层次理解算理,提高运算能力。
通过以上分析,不难看出图形语言的应用可让原本抽象的算理变得直观易理解,使学生能更好地掌握计算的本质。通过直观的图展示算理,可让学生在直观感知中明确计算方法,将学生的思维引入深度思考。
4. 巧用错误资源,夯实算理
课堂是一个动态发展的过程,学生在课堂的动态发展中产生一些错误在所难免,教师不能将目光只锁定在提醒或逐层设防上,应将学生制造错误的可能“扼杀在摇篮”中。鉴于此,在教学中教师应为学生提供广阔的思考空间,允许错误的发生,将一些典型错误作为教学资源,带领学生自主思错、纠错、辨错,探寻错误形成的真实原因,避免类似错误再次发生。
在教师的引导下,学生追根溯源探寻错误的成因与根治方法,能在错误中实现对知识的“再认识”,从而积累学习经验,夯实对算理的理解。
案例5 “三位数除以一位数”的教学
要求学生计算:612÷6。
如图3,“商中间存在0”的除法计算时学生容易出现错误,因此教师有意识地收集了几名学生的错误解法,带领学生一起辨析这几种算法的正确性。当学生发现问题后,教师追问:“这几种算法错在哪?应该怎么计算?”
学生以小组合作交流的方式与组内成员分享自己的想法,整个过程学生情绪高涨,表现出很高的积极性。
生1:第一种算法,该生漏写了商中间的0,因为十位上的1除以6不够,要将十位与个位上的数合起来一起除,但在写的时候,需要将中间的0添上。
生2:后面两种算法都将商的2写在十位上,它所代表的意思就是2个10,显然是错误的。
生3:口算就能發现这三种解法都是错误的,因为12×6=72,120×6=720,它们的乘积均非原式中的612,由此可确定这三个商都不正确。
生4:还可以借助分书的活动来分析这道算式,比如将612本书平均分成6份,首先考虑将600本书分成6份,每份就是100本;再将12本书分成6份,每份就是2本,因此每1份就是102本。
学生通过自主观察、思考、分析,实现了纠错,进一步深化了对“不够商1时商0”算理的理解。事实证明,合理用好学生的错误资源,能有效发散学生思维和提升学生的“四能”。
总之,算理、算法的教学是发展学生运算能力的关键,也是数学教学的核心。教师应与时俱进,应用科学的方法引导学生理解算理和感悟深度学习的本质,以促进其数学思维的发展和提升其数学核心素养。
