浆纱车速与压浆力对上浆率的影响关系

黄明 王矿 王静安 高卫东

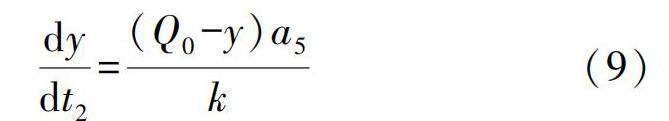
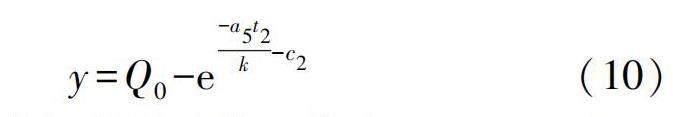
摘 要：现代浆纱机配备了浆纱车速-压浆力匹配调控技术，以稳定控制上浆率；目前普遍采用车速-压浆力线性调节方案，但缺乏一定的理论指导，往往会造成上浆率稳定性控制的效果不理想。为提高上浆率控制稳定性，对车速与压浆力对上浆率的影响关系进行研究。通过对浆纱过程中浆液的浸透与压出进行合理化假设，构建了车速、压浆力和上浆率的关系模型。基于该模型，提出不同车速下压浆力的求解方法，用于实现上浆率的稳定控制。该模型在浆纱实验数据中的拟合优度R²达0.8754，较线性模型高0.1388，验证了模型构建的合理性。依据该模型构建上浆率稳定控制方法，在不同车速下对压浆力进行调控实验，实测上浆率与设定值的平均相对误差为2.59%，有效实现了不同车速下的上浆率稳定控制。构建的车速、压浆力、上浆率关系模型，对解释车速与压浆力影响上浆率的机理具有一定的理论意义；基于该模型构建的上浆率稳定控制方法，为提高浆纱上浆率稳定控制水平提供了新的途径。

关键词：浆纱车速；压浆力；上浆率；模型构建；浆纱工艺

中图分类号：TS111.9 文献标志码：A 文章编号：1009-265X（2024）05-0065-08

收稿日期：20230829 网络出版日期：20231103

基金项目：中央高校基本科研业务费专项资金项目（JUSRP121030）；江苏省基础研究计划自然科学基金青年基金项目（BK20221061）

作者简介：黄明（1998—），男，安徽铜陵人，硕士研究生，主要从事浆纱技术方面的研究。

通信作者：高卫东，E-mail： gaowd3@163.com

浆纱是织造生产的关键工序，上浆后纱线的性能及其稳定性直接影响织造生产的效率^[1]。在浆纱的各项性能指标中，上浆率直接决定了浆纱的成本，同时与耐磨、毛羽、伸长等性能之间高度相关^[2-3]。保持合适且相对稳定的上浆率，是保障织造生产稳定的重要手段^[4]。在浆纱生产过程中，由于开机、了机、故障处理以及回潮率控制的需要，浆纱车速必然处在不断变化的状态中^[5]。而车速的变化直接影响纱线在通过浆槽时浆液的吸收与压出作用效果^[6]，导致上浆率波动。因此，现代浆纱机配备了车速-压浆力匹配调控技术，用于在车速变化时改变压浆力，在不同车速下形成相近的上漿效果，以实现上浆率的稳定控制^[7]。目前，车速-压浆力匹配调控技术中所采用的模型均为线性模型，即认为车速、压浆力对上浆率的影响满足线性关系^[8]。但由于缺乏一定的理论指导，实际控制过程中存在一定误差，从而引起车速变化时上浆率的稳定性不足。

如何稳定上浆率，一直是浆纱领域研究者关注的重点问题。王正虎^[1]研究了上浆工艺设置对浆纱的影响，认为明晰上浆工艺参数浆纱质量影响的特性和规律，是优化配置上浆工艺的关键。梁秀娟等^[4]研究了影响上浆率的主要因素，得到了浆纱上浆率﹑压出加重率和浆液含固率三者之间的关系，根据浆纱机的浸浆与压浆形式、所采用的浆液含固率和织物规格（线密度、组织结构、经纬密度等）来确定浆纱速度，通过计算“相当压浆力”来确定在该浆纱车速下的压浆力。窦玉坤等^[9]引入了多孔介质、孔隙率、渗透率等概念，从纱线结构的特点出发，结合渗流理论分析了细号纱上浆的工艺原理，指出了压浆力与上浆率之间关系模型的重要性。倪成彪等^[10]通过对收集的大量生产数据进行组合、分析、对比，探讨了上浆率与其主要影响因素间相关性，分析了各因素对上浆率的影响，建立了相应的回归方程。但目前研究对车速与压浆力在理论上如何影响上浆率尚未开展深入研究。

浆纱工艺过程是一个复杂系统，涉及多种因素的共同作用。本文对浆纱机上浆当中的复杂条件进行合理化假设，研究浆液在上浆过程中的吸附渗透和挤压流出过程，构建了浆纱车速与压浆力对上浆率的影响模型，通过浆纱全面实验所采集的数据验证了模型的有效性，最后将其应用于浆纱车速-压浆力对上浆率的匹配调控，有效实现了不同车速下上浆率的稳定控制。

1 车速与压浆力对上浆率的影响关系模型构建

为分析浆纱车速，压浆力对上浆率的影响机理，本文对浆纱过程进行合理化假设，主要假设如下：

a）假设纱线形状为直径不变的圆柱体，其内部力学性质一致。

b）浆纱过程中，浆液浓度、黏度等各项指标的波动可忽略不计。

c）在压浆辊与上浆辊的接触区域内压力分布均匀。

d）上浆过程可以视为浸浆和压浆两个独立的过程，互相不干扰。

1.1 纱线在浆槽中吸收浆液过程建模

当浆槽中的浆液量保持不变，纱线在上浆过程中浸入浆液的行程总长为常量。令该行程总长为浸浆长度，表示为L；令纱线浸入浆液的时间为浸浆时间，表示为t₁，则二者与浆纱车速v之间的关系可表示如下：

在某微元截面内，纱线对浆液的吸收量存在上限，即最大吸浆量，表示为Q₀；令任意时刻t时，该微元截面当前吸浆量为x；则此刻该微元截面的吸浆速度可表示为dx/dt₁。根据经验推断，在纱线吸收浆液的过程中，随着吸浆量逐渐接近最大吸浆量，吸浆速度逐渐降低。据此，假设吸浆速度与最大吸浆量和吸浆量之差呈线性关系，三者之间的关系可表示为：

式中：a₁为线性关系的系数。对式（2）积分求解，可得：

式中：c₁为积分求解所得系数。分析式（3），将e^－c₁记为参数d₁，可得：

分析极限情况，若吸浆时间为0，则纱线必然未吸收浆液，因此吸浆量也一定为0。将t₁=0，x=0代入式（4），可得d₁=Q₀；重新代入式（4）可得：

1.2 压浆辊对纱线的压浆过程建模

在压浆力的作用下，上浆辊与压浆辊的接触区域会因二者形变形成具有一定宽度的压榨区域，令该区域宽度为压榨宽度。纱线在通过压榨区域时受挤压作用，其体积被压缩，因而内部浆液被挤压流出。压浆辊挤压纱线示意如图1所示。

压榨宽度的大小通常会受到上浆辊与压浆辊的邵氏硬度、压浆辊包胶厚度、外圈橡胶材料泊松比等因素的影响。为简化问题，假设压榨宽度与压浆力大小成线性关系，则压浆力与压榨宽度的关系可表示为：

式中：w为压榨宽度，f为压浆力，a₂为线性关系的系数。

假设浆液只会在经过压榨区域时流出，则允许浆液流出的时间与压榨区域宽度成正比，与浆纱车速成反比。三者关系表示为：

式中：t₂为允许浆液流出的时间。

压浆过程中，浆液被挤压流出的过程较为复杂。首先，将纱线中所携带浆液视为流体对象，分析某浆液微元从纱线中受挤压流出的过程，可知该过程中浆液必须克服流体流速（浆纱车速v）所带来的阻力做功，从而运动离开纱线。参考流体力学中阻力与速度的关系理论^[12]，該阻力与流体速度的指数成正比。此外，纱线中浆液在受到压榨作用时，会在压榨区域与压浆辊或上浆辊形成碰撞，被迫减速至相反运动方向离开纱线，这一过程随着车速的提高而变得更为剧烈。对此现象，假设存在一个碰撞阻力，该阻力与车速成反比，描述了浆液因碰撞作用而产生的动力。综合上述阻力作用，可构建一项综合阻尼系数k，并假设浆液的压出速度与综合阻尼系数大小成反比，其表示如下：

式中：a₃为指数关系系数，a₄为反比关系系数。

根据经验推断，在浆液被压出的过程中，随着当前纱线吸浆量逐渐减小，浆液的压出速度逐渐降低。由此，假设浆液流出速度与纱线最大吸浆量与流出量之差成正比。令某微元截面在任意时刻压出的浆液量为y，则浆液的流出速度可表示为dy/dt₂，其计算模型可表示如下：

式中：a₅为比例关系系数。对式（9）积分求解可得：

式中：c₂为积分求解所得系数。将式（6）—（8）代入式（10）可得：

将e^－c₂记为d₂，将-a₂a₅记为d₃，将a₃+1记为d₄，可得：

式中：d₂、d₃、d₄均为待定系数。

1.3 车速与压浆力对上浆率的影响关系建模

令原纱重量为G，令上浆率为z，则由上浆率定义可知：

浸浆过程中，由于存在喷淋系统，以及预压的作用，使得纱线吸收浆液较为充分，因此本文提出忽略车速浆液吸收的影响。由此，假设任意速度下纱线剩余吸浆空间均可达到定值Q₁，则由式（12）—（13）可得：

记Q₀-Q₁为d₀，可得：

式中：d₀、d₂、d₃、d₄、a₄均为待定系数。

2 实验

2.1 实验材料和仪器

实验材料：醋酸酯淀粉（Starch acetate，工业级，宜兴市军达新材料科技有限公司）；聚乙烯醇（Polyvinyl alcohol，PVA0588，工业级，宜兴市军达新材料科技有限公司）；纯棉纱线（40 s，环锭纺，江苏悦达纺织集团有限公司）；氢氧化钠（Sodium hydroxide，NaOH，分析纯，国药集团化学试剂有限公司）。

实验仪器： XY2000-1B电子天平（常州市幸运电子设备有限公司）；GZX-9070MBE型电热鼓风干燥箱（上海博讯实业有限公司医疗设备厂）；C21-SDHC15X型电磁炉（浙江绍兴苏泊尔生活电器有限公司）；XSY617-700型实验用片纱浆纱机（江阴祥盛纺印机械制造有限公司）；NDJ-79型旋转黏度计（上海昌吉地质仪器有限公司）。

实验用片纱浆纱机采用单预压辊单上浆辊的浆槽型式^[13]，浆槽主要部件由导纱辊、预压辊、上浆辊、压浆辊以及喷淋装置组成。在浸浆阶段，经纱由经轴退绕后进入浆槽，首先受到预压辊与喷淋装置共同作用，接着随上浆辊运动浸入到浆液中，实现充分的浆液吸收；在压浆阶段，纱线通过由压浆辊与上浆辊挤压形成的压榨区域，完成压浆过程。该机型的浆槽型式，与本文建立的浸浆与压浆过程模型相一致，其示意如图2所示。

2.2 实验方法

2.2.1 浆液的制备

根据浆纱机浆槽容量大小，配制含固率为8%的浆液40 kg。称取1.28 kg聚乙烯醇（PVA-0588）和1.92 kg醋酸酯淀粉分别加入到水中，搅拌器转速为800 r/min，搅拌时间为30 min使浆料完全溶解。溶解的浆液转移至调浆桶当中混合搅拌，在95 ℃温度下搅拌糊化2 h。上浆实验和上浆率测定均在温度（25±2） ℃，湿度（65±5）%的环境下进行。浆纱过程中实测浆液黏度稳定在（15±2） MPa·s。

2.2.2 纱线上浆

使用XSY617-700型片纱浆纱机对纱线进行上浆实验，其简要步骤为：

a）打开总电源及浆纱机电源开关。

b）依次打开卷绕电机，牵引电机，合并烘电机，预烘电机，上浆电机，喂入电机。根据使用的经轴选用对应的退绕电机。

c）打开经轴退绕画面，输入相应的初始卷径和当前卷径；打开压浆力画面，输入实验所需的压浆力；打开温度控制画面，设置烘筒温度、浆槽温度；打开伸长率设置画面，设置实验所需伸长率。

d）将制备好的浆液输入浆纱机浆槽中；开启浆槽循环开关。

e）点击启动和加速按钮，使浆纱车速达到实验所需速度对纱线进行上浆。

2.2.3 纱线取样

在浆纱机的浆纱车速和压浆力达到设定值并稳定运行后，进行取纱操作，取样长度约为1500 m，相同工艺条件下取3个样以待测试。

2.2.4 上浆率测试

测试步骤为：

a）取样称重：分别卷绕 1500 m左右的浆纱，然后将每个纱线样品分别放入标记好的无纺过滤袋中，再放进105 ℃烘箱中烘干至恒重，使用电子分析天平称取纱线试样的质量。

b）退浆操作：配制适量质量分数为2%的氢氧化钠溶液，将溶液倒入电磁锅中加热，待溶液煮沸后，将每个装有浆纱样品的无纺过滤袋依次放入溶液，边煮边搅拌10 min，然后捞出用清水漂洗干净。

c）烘干称重：将冲洗干净的纱线样品放进 105 ℃烘箱中烘至恒重，取出称重。

d）毛羽损失率测定：取1500 m左右的原紗样品3个，对原纱进行相同的退浆操作，毛羽损失率用原纱煮练前后的干重按式（16）计算，浆纱上浆率按式（17）计算：

式中：β表示毛羽损失率，%；G_q表示原纱煮练前干重，g；G_h表示原纱煮练后干重，g。

e）上浆率计算：采用如下公式计算上浆率：

式中：z表示上浆率，%；J₁表示浆纱退浆前干重，g；J₂表示浆纱退浆后干重，g。

2.2.5 浆纱实验方案

为获取不同车速和压浆力组合下的上浆率数据，浆纱车速参数设置6个水平，分别为10、20、30、40、50、60 m/min，即每隔10 m/min设置一个水平。对压浆力参数设置6个水平，分别为6、10、14、18、22、26 kN，即每隔4 kN设置一个水平。对两个参数各个水平的所有组合进行全面实验。

2.3 实验数据处理

对不同车速与压浆力下的浆纱上浆率结果进行本文模型的拟合，拟合曲面图如图3（a）所示；对数据进行线性函数拟合，拟合数据曲面图如图3（b）所示。

本文所构建模型拟合所得函数表达式为：

其中：为避免因f和v所在区间对模型拟合造成的误差放大，分别以30 kN和120 m/min作为f和v的最大值进行数值归一化。最终模型的拟合优度R²值达到0.8754，表明模型对实验数据具有良好的表达能力。由图可知，在较低的压浆力下，车速的变化对上浆率的影响相对明显。随着压浆力的不断提高，车速变化所带来的上浆率变化减小。其原因主要是较小的压浆力对浆纱的挤压作用不强，此时尽管车速仍会影响压浆时间，但由此产生的压浆效果差异不大，因而对上浆率的影响较小。在较高的压浆力下，压辊对浆纱的挤压作用较强，因此压浆作用效果更易受到压浆时间的影响，因而车速对上浆率的影响变强。

线性模型拟合所得函数表达式为：

z=12.48－0.2662f+0.06367v（19）

线性模型的拟合优度R²值为0.7366。相比于本文所构建的模型，线性模型对数据的拟合度明显更低，这表明在实验数据中，本文所构建模型对车速、压浆力和上浆率的关系表达更为合理。

2.4 上浆率控制效果验证

基于本文构建的车速、压浆力对上浆率的影响关系模型，可推导计算出车速变化时的压浆力调节方案。即给定目标上浆率z₀，将式（18）进行变量代换、变形，可得如下计算公式：

同理对线性模型进行相同代换变形，可得线性指导方案的计算公式如下：

f=46.88－3.7566z₀+0.2392v    （21）

将不同车速v的取值分别代入式（20）—（21），可得两种以稳定上浆率为目标的压浆力取值方案。

为验证方法的有效性，参照纯棉纱线使用淀粉为主浆料，PVA为黏合剂上浆时常用上浆率^[11]，取目标上浆率z₀∈{8%，9%，10%，11%，12%}，分别采用本文所构建模型（方案1）与线性模型（方案2），基于上述方法计算不同车速v∈{10 m/min，20 m/min，30 m/min，40 m/min，50 m/min}下恒定上浆率所需的压浆力取值，并检验据此进行上浆所得纱线的上浆率是否稳定在目标值附近。作为示例，表1所列为以10%为目标上浆率时，不同车速下压浆力由模型1与模型2计算所得的取值。

在目标上浆率z₀取值分别为8%、9%、10%、11%、12%时，根据前述实验方法，在车速v分别取值为10、20、30、40、50 m/min的条件下进行实验，不同车速下所采用压浆力分别由模型1和模型2推导计算所得。实验所得纱线的上浆率测试结果如图5所示。

如图4所示，在不同目标上浆率下，线性模型方案（方案2）所调控的上浆率与目标上浆率相比，其误差和波动都明显较大。相较而言，本文的模型方案（方案1）所调控上浆率更贴近目标值。在不同目标上浆率下，线性模型方案与本文模型方案所得控制上浆率误差如表2。

由表2可知，方案2调控上浆率的平均相对误差的平均值为16.31%，显著低于方案1调控上浆率的平均相对误差的平均值2.59%，表明方案1调控的上浆率与目标上浆率差异小，验证了在不同目标上浆率要求下，本文所构建方法对上浆率稳定控制均具有良好的效果。方案1所调控上浆率的CV值为2.55，显著低于方案2的CV值13.86，表明对于不同目标上浆率的稳定控制，本文所构建方法具有良好的普适性。综上所述，基于本文所构建模型的上浆率稳定控制方法，有利于实现不同车速下的上浆率稳定调控，能够满足浆纱生产的稳定性要求，具有良好的产业应用价值。

3 结论

本文通过从浸浆和压浆两个过程来分析浆纱工艺，对浆纱条件进行了合理化的假设，建立了浆纱车速、压浆力对上浆率影响关系的数理模型。基于不同车速与压浆力下获取的浆纱实验数据，对本文所构建模型与传统线性模型进行数值拟合，验证本文模型的有效性。基于该模型构建了不同车速下的上浆率稳定控制方法，在不同目标上浆率下开展实验，验证方法的有效性与普适性。本文得到的主要结论如下：

a）本文模型在浆纱实验数据上的拟合优度R²值为0.8754，高于线性模型的0.7366，表明本文模型较线性模型能更好地解释浆纱车速、压浆力、上浆率的内在作用关系，一定程度上阐明了浆纱车速与压浆力对上浆率的影响机理。

b）基于本文模型构建上浆率稳定控制方法，所得上浆率的误差平均值为2.59%，低于线性方案的16.31%；所得上浆率的误差CV值为2.55，低于线性方案的13.86。表明该方法具有良好的有效性与普适性，对改进当前上浆率稳定控制方法提供了新的途径。

本文构建了压浆力、浆纱车速与上浆率之间的关系模型，但模型仍需较多的实验数据点以取得良好的拟合结果，限制了该模型对于不同纱线与浆纱条件的泛用性。对此，未来工作还需着重研究模型拟合过程的简化，以提升相应控制方法在生产实践中的实用价值。

参考文献：

[1]王正虎.上浆工艺设置对浆纱的影响[J].纺织导报，2015（11）：76-81.

WANG Zhenghu. The effect of process settings on sizing quality[J]. China Textile Leader， 2015（11）： 76-81.

[2]洪仲秋.上浆率的设定及其影响因素分析[J].棉纺织技术，2007，35（10）：17-21.

HONG Zhongqiu. Set ofsizing percentage and its influence factor[J]. Cotton Textile Technology， 2007， 35（10）： 17-21.

[3]郭圈勇，崔秀艳.稳定浆纱上浆率的控制措施[J].棉纺织技术，2017，45（7）：60-63.

GUO Quanyong， CUI Xiuyan. Control measures of stabilizing sizingpercentage[J]. Cotton Textile Technology， 2017， 45（7）： 60-63.

[4]梁秀娟，牛建设.浆纱上浆率的主要影响因素及保证措施分析[J].中原工学院学报，2010，21（4）：73-75.

LIANG Xiujuan， NIU Jianshe. Main affect factors and ensuring measurement analysis for sizing rate[J]. Journal of Zhongyuan University of Technology， 2010， 21（4）：73-75.

[5]黃彦萍.影响上浆质量的几个因素[J].棉纺织技术，2018，46（7）：10-13.

HUANG Yanping. factors of affecting sizing quality[J]. Cotton Textile Technology， 2018， 46（7）： 10-13.

[6]佟昀.上浆要素内在关系及其对高压上浆工艺的影响[J].纺织学报，2008，29（12）：30-33.

TONG Yun. Correlation of sizing factors and their influence

on high pressure sizing[J]. Journal of Textile Research， 29（12）： 30-33.

[7]萧汉滨.新型浆纱机与高压上浆工艺路线研究[J].棉纺织技术，2002，30（6）：8-11.

XIAO Hanbin. New sizing machine and its processing route of high-pressure[J]. Cotton Textile Technology， 2002， 30（6）： 8-11.

[8]闫文君，郭雨，朱博，等.车速与压浆力线性变化对浆纱性能的影响[J].棉纺织技术，2020，48（1）：4-8.

YAN Wenjun， GUO Yu， ZHU Bo， et al. Influence of sizing velocity and squeezing pressure linear change on sizing property[J]. Cotton Textile Technology， 2020， 48（1）： 4-8.

[9]窦玉坤，毛雷，刘士广.影响浆液浸透效果的因素分析[J].棉纺织技术，2005，33（11）：55-57.

DOU Yukun， MAO Lei， LIU Shiguang. Influence factors on size imbue effect[J]. Cotton Textile Technology， 2005， 33（11）： 59-61.

[10]倪成彪，宋瑞忠，熊森，等.上漿率与其主要影响因素间相关性的探讨[J].棉纺织技术，2014，42（8）：63-66.

NI Chengbiao， SONG Ruizhong， XIONG Sen， et al. Discussion of sizing percentage and its main effect factors correlation[J]. Cotton Textile Technology， 2014， 42（8）： 63-66.

[11]SINGH M K. Preface[M]//Industrial Practices in Weaving Preparatory. Amsterdam： Elsevier， 2014.

[12]龙天渝，童思陈.流体力学[M].重庆：重庆大学出版社.2018.

LONG Tianyu， TONG Sichen. LIUTI LIXUE[M]. Chongqing： Chongqing University Press， 2018.

[13]高卫东，姜为民，王静安，等.国产浆纱机的技术发展历程与展望[J].棉纺织技术，2023，51（10）：41-46.

GAO Weidong， JIANG Weimin， WANG Jing'an， et al. The technological development history and prospects of domestic sizing machines[J]. Cotton Textile Technology， 2023， 51（10）： 41-46.

Influence of sizing machine speed and squeezing force on sizing rates

HUANG Ming， WANG Kuang， WANG Jing'an， GAO Weidong

（College of Textile Science and Engineering， Jiangnan University， Wuxi 214122， China）

Abstract： Sizing is a crucial process in weaving production， and its quality directly impacts the production efficiency of weaving machines and the quality of the fabric. The technology of sizing machines has a significant influence on the sizing effect. Among them， regulating the sizing machine speed and squeezing force is the top priority of the sizing process. During operation， the speed of the sizing machine is in a constantly changing state due to the requirements of start-up， stopping， fault treatment， and moisture regain control. Changes in the speed of the sizing machine directly affect the adsorption and squeezing of size liquor when the yarn passes through the size box， causing fluctuations in the sizing rate. Therefore， modern sizing machines are equipped with speed-force matching control technology， which can adjust squeezing force when the speed changes， thereby achieving stable sizing rates and the same sizing effect. At present， the schemes used in the matching control technology of sizing machine speed and squeezing force are all linear. Due to the lack of theoretical basis for this linear relationship and the reliance on manual experience in calibrating the linear model， there are certain errors in the actual control of sizing rates.

To better control the sizing rate by controlling the squeezing force when the speed of the sizing machine changes， we simplified the warp sizing process into the yarn immersion and squeezing process by making rational assumptions about the sizing problem. Firstly， in the analytical discussion of the immersion process， a functional relationship between immersion time and the space in which the yarn has absorbed the size liquor was established. Then， through the in-depth investigation of the mechanism of the squeezing process， the functional relationship between the amount of sizing liquid squeezed and the speed of the sizing machine and the squeezing force was constructed. A model of the relationship between sizing machine speed and squeezing force on sizing rates was constructed according to the aforementioned process. Six levels were set for sizing machine speed and squeezing force respectively， comprehensive experiments were carried out on all combinations of each level of these two parameters， and a total of 36 data were obtained for fitting the constructed model. The R²value of the goodness of fit reaches 0.8754， which verifies that the model proposed in this paper elucidates the mechanism of the influence of sizing machine speed and squeezing force on sizing rates to a certain extent.

To check the application effect of the model from the practical perspective， the sizing rates of 8%， 9%， 10%， 11%， and 12% were taken as the target sizing rates， and based on the model constructed in this paper， the values of squeezing force were deduced and calculated under the sizing machine speeds of 10， 20， 30， 40， and 50 m/min， and the values were calculated based on the model constructed in this paper. And the sizing experiments were carried out under the corresponding processes. The results show that when the scheme modeled in this paper is used， the average relative error of the measured sizing rate is 2.59%. The average relative error of the measured sizing rate is 16.31% when the linear scheme is used for sizing under the same conditions. It shows that the model scheme constructed in this paper is significantly better than the linear model scheme in controlling the sizing rate. It is beneficial to realize the stable regulation of sizing rates under different vehicle speeds， and can meet the stability requirements of sizing production. It has good industrial application value.

Keywords： sizing machine speed; squeezing force; sizing rate; model building; sizing process