逻辑推理素养培养视角下的高中数学课堂教学

王世琼

摘要：培养学生的逻辑推理素养，既能够助力学生对数学知识的有效掌握，也能够帮助学生掌握推理技巧与推理方法.据此，笔者将从高中数学逻辑推理素养培养的基本原则与基本策略入手，阐述如何有效开展高中数学课堂教学.

关键词：逻辑推理；高中数学；课堂教学

中图分类号：G632文献标识码：A文章编号：1008-0333（2024）12-0047-03

逻辑推理素养是指，在教学中教师应从事实和命题处入手，根据相应的规则推理获得其他命题的一种数学素养.在逻辑推理素养中，一般将其分为两类：其一为“特殊到一般”推理，包括有归纳推理、类比推理；其二为“一般到特殊”推理，包括有演绎推理.

1 高中数学逻辑推理素养培养应遵循的基本原则

1.1 重视逻辑推理习惯的有效引导

在培养学生逻辑推理素养的过程中，教师也应重视对学生的引导，即给到学生一定的思路与启发，由学生进行自主思考.只有这样，学生才能真正具备逻辑推理能力.在教师的引导中，学生积极思考，努力整合所学知识，做到严谨推理过程，养成良好的推理习惯.

1.2 重视逻辑推理规律的清晰讲解

在培养学生数学逻辑推理能力的过程中，教师需要重视对逻辑推理规律的清晰讲解.对高中学生而言，高中数学知识具有一定的难度，要想实现对知识的深入理解，学生应扎实掌握基础知识，在此基础上，教师讲解的逻辑推理规律才能够被学生有效理解.因此，在高中阶段的数学课堂中，要想实现对学生逻辑推理素养的培养，教师应

重视逻辑推理规律的讲解，并在教学中有意识地引导学生厘清推理问题的内部逻辑.

1.3 尊重学生逻辑推理的发展需要

对学生而言，从小学到初中阶段的学习，是其自身思维发展的重要过程，这是学生必须经历的学习过程.而到了高中阶段，学生的需求会增多，这是学生思维发展的需要，更是学生实现深入学习的必经之路.为此，教师应在教学中尊重学生的发展需要，努力讲好关于逻辑推理的课程，让学生掌握逻辑推理，并引导学生借此提高数学学习能力，努力丰富自己的知识和内涵.

2 高中数学逻辑推理素养培养应实施的基本策略

2.1 设置情境，认知逻辑推理

在认知逻辑推理内容的过程中，教师需要运用情境教学手段，为学生设置关于逻辑推理的教学情境，以此来引导学生正确认知逻辑推理.在此基础上，教师实施的教学活动才是有效、有意义的.在设置教学情境时，教师可以结合学生的实际情况设置故事情境、生活情境、问题情境等不同形式的教学情境，从而实现对学生逻辑推理能力的有效认知[1].

以人教版数学必修第一册第一章中《1.3 集合的基本运算》为例.在本章节的学习中，学生应借助对以下知识内容的学习，做到对逻辑推理的基本认知.具体如下：准确理解、掌握、运用交集、并集、全集、补集的知识，知晓不同集合之间的关系运算，从而实现对逻辑推理知识的初步认知.基于此，在教学实践中，教师可以通过创设生活情境的方式，引出本次学习的知识内容.首先，了解并集与交集.教师可以展示生活中常见的标志：公共交通上的老弱病残孕专座，并让学生推理四种情况之间的关系.在推理分析中，学生可以从每个字所代表群体的具体含义入手，如“老”是指老人，“弱”是指弱小的儿童，“病”是指病人，“孕”是指孕妇.在知晓具体含义后，学生便能够发现其中的集合关系，即这四类人是并集关系，只要满足其中一个条件，便可以坐在该座位上.再如“多快好省”曾是国家建设的宣传标语，现为许多商家使用的广告语.在推理分析中，学生依旧需要从每个字的具体含义入手：“多”是指数量多，“快”是指速度快，“好”是指质量好，“省”是指成本省.但是，这四条标准之间的关系还是并集吗？答案是否定的，这四条标准是交集关系，即需要同时满足四条标准的要求，才能够让商家做到吸引消费者的目的.

在上述情境中，教师借助生活实例设置了教学情境，并引导学生对情境内容进行分析与推理，以此促进学生对并集与交集知识的掌握，并从集合知识中获得对逻辑推理的初步认知，有效建立逻辑推理意识.

2.2 讲解例题，感受逻辑推理

在数学课堂中，教师需要借助例题讲解新知识、总结旧知识，让例题成为新知识与旧知识之间的桥梁.因此，在逻辑推理的数学课堂上，教师需要借助对例题的讲解，引导学生感受逻辑推理、理解逻辑推理.

以人教版数学必修第二册第六章中《6.2.1 向量的加法运算》为例.在本次课程的学习中，学生需要借助对实例与平面向量的几何意义，掌握向量的加法运算法则，并能够实现对加法运算法则的熟练运用.教师可以先引导学生进行类比思考：正常的数字可以进行加减乘除的运算，那么，向量是否也可以像数字一样进行加减乘除的运算呢？以此为思考基础，教师可以借助具体事例引导学生举行推理与探究[2].如题（图1）：已知四边形ABCD为梯形，且AD∥BC，对角线AC与BD相交于点O，则OA+BC+AB+DO=？

在推理解决该问题时，教师要引导学生体会推理的过程，即向量與向量间的加法运算法则，具体计算推理过程如下：OA+BC+AB+DO =DO+OA+AB+BC=DA+AB+BC=DB+BC=DC.在本题的计算中，学生需要根据题目中提供的信息，找到不同向量之间的关系，如DO与OA是在△DOA中，而根据向量加法的三角形可知DO+OA=DA，如此便可以继续根据向量加法的三角形法计算△DAB中涉及的向量关系，经过层层推导，获得最终的结果.其实，解题的关键在于学生能够充分理解向量加法的三角形法则，并根据法则完成向量之间的推导.

因此，在引导学生感受逻辑推理时，教师需要借助具体例题，为学生清晰地解释每一个推理步骤的依据.这样，学生在掌握习题的同时，对向量加法的三角形法则也能够熟练掌握.2.3 设计问题，尝试逻辑推理

在实际教学中，教师通过设计问题，引导学生对逻辑推理的问题进行思考，并尝试自主解决逻辑推理问题.对学生而言，尝试自己解决逻辑推理问题，不仅是对自身知识掌握情况的考验，也是促进自身能力进步的重要途径.学生需要依靠自己完成知识的获取，这也是学生掌握逻辑推理能力的重要一步.因此，在教学中，教师应积极设计问题，引导学生进行逻辑推理.

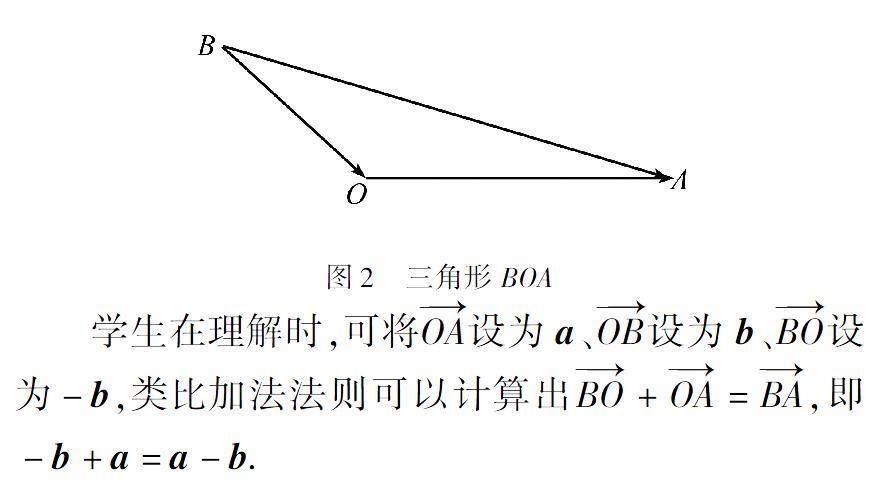
以人教版数学必修第二册第六章中《6.2.2 向量的减法运算》为例.在本课程的学习中，学生应掌握相反向量的概念，理解并能够运用向量减法的运算法则.对此，在上文学习向量加法的基础上，教师可以借助问题的设计，引导学生自主思考，让学生尝试自主完成问题的推理与解决.首先，教师可以借助减法运算的知识，设置类比问题，如根据数的运算的减法法则，能否获得向量的减法法则？如果能，应该怎样定义呢？如何理解与运用向量减法的三角形法则？是否可以类比向量加法的三角形法则呢？其次，学生应对问题进行类比思考，并讲出最后的答案.理解前两个问题，需要清楚减法是加法的逆运算，即减去一个数等于加上这个数的相反数，类比推理可得“减去一个向量等于加上这个向量的相反向量”，如a-b= a+（-b），同理可以获得向量减法的三角形法则.如图2中所示：

学生在理解时，可将OA设为a、OB设为b、BO设为-b，类比加法法则可以计算出BO+OA=BA，即-b+a=a-b.

通过上述推理，学生便可以获得关于向量减法的三角形法则，并能够理解其蕴含的意义，进而在题目中熟练运用.

2.4 反思过程，把握逻辑推理

在逻辑推理的过程中，学生应对自己的推理过程有切实的把握，既要有逻辑推理的思路，也要有对逻辑推理过程的反思.只有这样，学生才能在数学学习中真正掌握逻辑推理知识，实现对逻辑推理知识的有效运用.因此，在数学课堂上，教师应引导学生养成反思逻辑推理过程的习惯，在推理过程中做到严谨细致，以此来锻炼自己的推理思维，实现对推理知识的有效运用，进而提升推理能力.

以人教版数学必修第二册第六章中《6.2.1 向量的加法运算》和《6.2.2 向量的减法运算》为例.在上文的阐述中，笔者借助具体的实际案例，从为学生详细讲解向量的加法运算，到学生在教师的指点下自主完成加法运算的学习，不仅锻炼了学生的学习能力，更重要的是让学生学会进行知识的类比学习，能够在一定逻辑思维的促进下，实现独立自主的学习.但是，在学习向量加法与减法的过程中，学生需要对自己计算的内容、学习的知识进行及时的反思与总结，主动将思想向逻辑推理靠拢，这样才能提升逻辑推理能力.在学习中，笔者认为，学生应将重点放在理解向量加法的三角形法则和向量减法的三角形法则.通过题目的练习，我们会发现，向量计算最终都会归入三角形中，不论题目初始时的图形是平行四边形，还是梯形等其他图形，都需要将最终的计算落实在三角形上.故而，学生在运用的过程中，应思考如何将题目给的信息与最后需要获得的结果进行关联，即充分运用向量加法与减法的三角形法则.

对此，教师应在教学中及时将上述知识内容与学生分享，并提醒学生注意计算的过程.这样，学生在解题时，便可以围绕三角形法则寻找解题思路，从而确保整个计算过程的严谨、细致，促进学生逻辑推理能力的提高.

3 结束语

综上，逻辑推理素养是高中学生必须具备的一种数学核心素养，是其深入学习数学知识、提高数学思维能力的重要素养.因此，在文章中，笔者从设置情境、讲解例题、设计问题、反思过程四个方面入手，阐述了高中数学逻辑推理素养应实施的基本策略.該策略的实施不仅可以让学生具备逻辑推理素养，更重要的是可以培养学生养成运用逻辑推理的习惯，这对学生数学核心素养和数学综合能力的提升有重要意义.

参考文献：

[1] 张刘珊.逻辑推理素养培养视角下的高中数学课堂教学策略[J].高考，2022（27）：89-92.

[2] 杨海山.基于逻辑推理素养的高中数学课堂教学对策探析[J].数学学习与研究，2022（24）：26-28.

［责任编辑：李璟］