基于多策略改进鲸鱼算法的船舶推力分配方法

刘明

摘 要：船舶动力定位推力分配求解是一种复杂的多约束多目标优化问题，鲸鱼优化算法（WOA）处理该类问题较传统推力分配算法计算更简便、精度更高，但以牺牲时间为代价，需解决实时可靠收敛问题。针对上述问题，提出一种改进鲸鱼推力分配算法，通过采用等式约束项的特解系数为个体变量，降低搜索空间维度和范围，为算法获取可靠解和快速收敛奠定基础；通过空间区块化和“精英”筛选法初始化种群，增加初始种群分散性和“精英”个体数量，提高寻优效率和收敛稳定性；引入动态种群边界获取合理的搜索空间，提高算法收敛速度；最后运用类梯度法进行种群更新，模拟区域遍历搜寻，以较少迭代次数获取可靠解。以Cybership Ⅲ船模为对象进行仿真验证，结果表明该算法可行，具有较好的实时性和稳定收敛性，提高了推力分配性能。

关键词：推力分配； 动力定位； 鲸鱼算法； 多约束多目标优化

中图分类号：TP301.6; U664   文献标志码：A

文章编号：1001-3695（2024）03-027-0831-05

doi：10.19734/j.issn.1001-3695.2023.07.0307

Ship thrust allocation method based on multi-strategy improved whale algorithm

Liu Ming1，2

（1.Nantong University Xinglin College， Nantong Jiangsu 226236， China; 2. School of Electrical Engineering， Nantong University， Nantong Jiangsu 226019， China）

Abstract：The solution of ship dynamic positioning thrust allocation is a complex multi-constraint and multi-objective optimization problem. The whale optimization algorithm（WOA） is more convenient and accurate in handling this type of problem compared to traditional thrust allocation algorithms， but at the cost of time， and needs to solve the problem of real-time reliable convergence. Aiming at the above problems， this paper proposed an improved whale thrust allocation algorithm. This algorithm used the particular solutions coefficients of the equality constraints as individual variables， reducing the search space dimension and range， laying the foundation for obtaining reliable solutions and fast convergence of the algorithm. In addition， the population initialization adopted space block and “elite” screening methods to increase the initial population dispersion and the number of “elite” individuals， improving optimization efficiency and convergence stability. It introduced dynamic population boundaries to obtain a reasonable search space and improve the algorithms convergence speed. Finally， it proposed a gradient method population updating method to simulate region traversal search and achieve less iterations to obtain reliable solutions. This paper took the Cybership Ⅲ ship model as an example for simulation verification.The simulation results show that the thrust allocation method is feasible， has good real-time performance and stable convergence， and improves thrust allocation performance.

Key words：thrust allocation; dynamic positioning; WOA; multi-constraint and multi-objective optimization

0 引言

隨着陆地资源的枯竭，人类逐渐开始探索与开发海洋资源，动力定位船舶应运而生并得到了长足发展［1］。动力定位系统装备作为高技术含量的海工装备在海洋应用等领域发挥着越来越重要的作用，推进系统作为船舶动力定位系统的执行机构，发挥着关键作用，合理的推力分配不仅能够提高船舶的定位能力，还可以提高船舶运行的经济性，因此推力分配问题的研究具有现实应用意义和价值。

推力分配的求解方法有多种，比如分配逻辑法［2］、组合偏置法［3］、推力器分组法［4］、伪逆法［5］、滤波和奇异值分解法［6］、序列二次规划（SQP）［7，8］推力分配策略等，传统推力分配方法灵活性较差、多目标综合优化能力有待提高，比如伪逆法主要实现能耗最小化而忽视其他性能指标，序列二次规划法需要将推力分配数学模型配成二次型，计算比较复杂，且存在近似计算而引入偏差问题。随着群智能优化算法的兴起，为推力分配求解提供了另一种路径，由于该类算法不依赖于对象问题的代价函数和约束形式，使得传统推力分配中存在的问题都可迎刃而解。目前，研究人员主要采用遗传算法［9～11］和粒子群算法［12，13］进行推力分配研究，极少文献涉及混合蛙跳算法［14］、蜂群算法［15］、差分进化算法［16］和鱼群算法［17］等。文献［9］通过种群初始化，继承了上一时刻的精英个体和自适应改变交叉，变异概率对遗传算法进行改进，提高了算法优化精度和速度；文献［10］提出一种非支配排序遗传算法，通过引入微分变异算子提高算法局部寻优能力；文献［11］采用遗传算法，通过动态设置可行域，提高推力分配经济性；文献［12］在直接搜索法和伪逆搜索法的基础上提出一种自选变量粒子搜索法，提高算法实时性和收敛性；文献［13］以粒子群算法为基础，混合遗传算法中的交叉和变异策略进行推力分配求解；文献［14］在常规蛙跳算法基础上引入混沌初始化和收缩因子更新规则，提高算法多样性和收敛速度；文献［15］提出一种具有混沌搜索的自适应混合蜂群算法，该算法能够自适应切换搜索机制，降低推进器能耗；文献［16］在原始差分进化算法的基础上提出利用历史参数自适应调整控制参数的差分进化改进算法，降低机械磨损，提高推力分配精度；文献［17］提出模拟退火全局人工鱼群算法，改善算法突跳能力和后期收敛精度。这些研究成果提高了推力分配性能，然而这些算法在实时性收敛和稳定性方面尚需提高，以进一步增强算法的工程实用性。一方面上述文献研究的重点是群智能算法本身的改进，种群个体变量选择研究甚少，大部分直接采用推力分配输出量为个体变量，该方式一般需要更多的迭代次数保证收敛性，且存在不收敛的风险；另一方面，现有改进算法难以解决以较少迭代次数获得可靠解的实时性需求问题；此外，這些文献未对算法的稳定性和可靠性进行研究分析，而这是算法在工程应用中的关键因素之一。

为了实现较少迭代次数获取稳定可靠的最优解，本文提出一种多策略改进的鲸鱼算法用于推力分配求解。该改进算法研究了一种满足严格等式约束的个体变量为算法快速收敛和可靠收敛奠定基础；提出一种空间区块化和“精英”筛选种群初始化方法，在提高算法全局寻优能力的同时降低对初始值的敏感性，有利于获取稳定输出；动态个体边界的设计能够获取合理搜索空间，提高算法收敛快速性；个体类梯度法更新策略提高算法单步寻优遍历性，是解决算法可以在较少迭代次数获取全局最优解的关键。最后通过Cybership Ⅲ船模进行仿真，验证了本文算法的可行性及优越性。

1 推力分配模型

1.1 推力分配问题约束条件和数学模型

推力分配优化是在一定约束条件下求解代价函数极小值的问题，数学模型通常包括代价函数、等式约束项和不等式约束项。

代价函数通常包括推进器的磨损、能耗、系统的奇异结构等，具体可以表示为［14］

3.4 改进算法的逻辑流程

a）初始化船舶参数包括结构参数、状态参数、物理条件约束参数和权值系数等。

b）根据动态个体边界机制计算个体极值，在此基础上利用空间区块化和“精英”筛选策略初始化种群。首先根据个体边界划分若干对称的空间区块；然后每个空间区块利用式（12）（13）独立生成该空间区块个体及对称空间区块个体；最后将每个空间区块种群按个体适应度值从小到大进行排序，选择前若干个个体作为最终初始种群。

c）更新参数P（随机数）、C、a和A的值。P大于设定值（本文取0.5）时，根据式（10）执行螺旋气泡捕获猎物策略；P小于设定值且A≥1时，根据式（11）执行搜索猎物策略；P小于设定值且A＜1时，根据式（8）执行包围猎物策略。

d）计算个体适应度值，更新最优个体位置。

e）选取若干最优个体，按照类梯度法个体更新策略逐一进行局部深度搜索，并更新最优个体位置。

f）判别是否达到最大迭代次数，是则跳至步骤g），否则跳至步骤c）。

g）输出推力分配结果，跳至步骤b）进行下一周期推力分配优化求解。

4 仿真实例分析

本文以船模Cyber shipⅢ为对象，该船舶结构如图1所示，部分推进器参数如表1所示。

1）仿真实例1

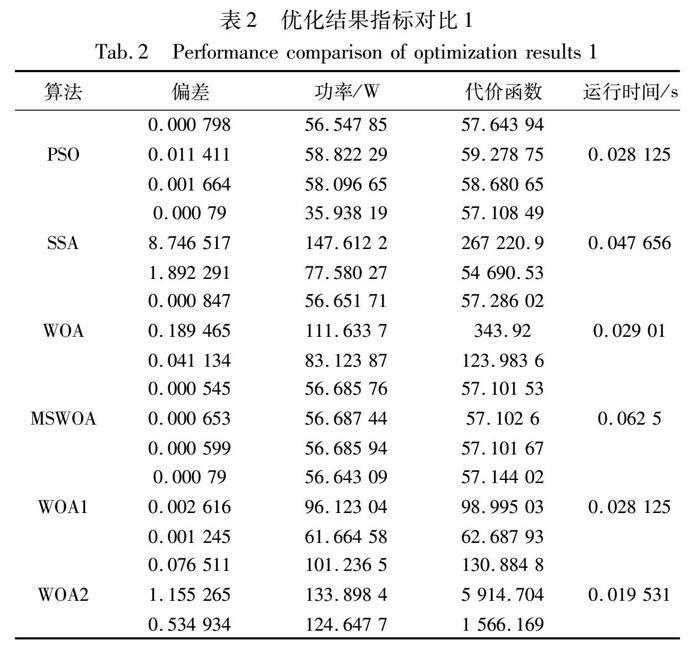
本实例采用单点静态测试，选取的期望力和力矩分别为5 N、1 N、1 N·m，对比算法有PSO、SSA、常规的WOA、MSWOA，这些算法个体变量都采用本文提出的方法；此外为验证个体变量选择对测试结果的影响，对比算法还选取了WOA1（拓展推力为个体变量，并采用文献［6］中严格等式约束模式）和WOA2（推力和角度为个体变量）。除了本文算法，其他算法初始化采用混沌算子，代价函数设置相同（包括能耗项、偏差项、机械磨损项和奇异项），每种算法连续运行20次，最大迭代次数分别取10和100。仿真处理结果分别如表2、3所示。

表2和3中的运行时间为平均时间，其他指标每个算法中三个数据自上而下分别为20次运行结果中最小值、最大值和平均值。由表2可知，当迭代次数较少时，SSA和WOA2寻优结果较差，它们在寻优过程中存在不收敛情况，PSO比WOA和WOA1效果更好。本文算法除了运行时间，其他指标都是最优的，更关键的是其收敛的可靠性高（最大值、最小值和平均值相差很小，即运行结果稳定可靠）。由表3可知，当迭代次数较大时，SSA和WOA2寻优结果得到较大改善，但WOA2仍然存在不收敛风险，可见以推力和角度为个体变量存在较大的不收敛风险，而且需要较大迭代次数来确保寻优效果，工程实用性较差，其他算法都获得了较好的寻优效果。本文算法寻优的偏差最小，而且各指标的最大值、最小值和平均值一致，说明算法具有很强的稳定性，虽然迭代次数同等时本文算法运行时间最长，但本文算法能以更少迭代次数获得比其他算法较大迭代次数更优的效果，因此实际应用中可以设置较低迭代次数进行推力分配寻优。

2）仿真实例2

本实例进行平稳动态测试，对比算法除了实例1中部分算法外，还引入了传统的SQP推力分配算法。代价函数设置相同，每种优化算法连续运行20次，本文算法迭代次数取10，其他优化算法迭代次数取100，仿真处理结果如表4、图2所示。

由表4可知，平稳状态下PSO、WOA和MSWOA都取得了理想优化结果，但MSWOA在耗时更少的情况下，偏差和功率指标更优越，稳定性更好；SSA和WOA1两种算法在较少迭代次数情况下寻优效果不理想，稳定性差，其中SSA偏差是个别周期寻优结果差引起的，WOA1则在整个周期呈现出波动偏差，消耗功率也最高，表明个体变量采用MSWOA更有利于获取最优解。图2中SQP绝对误差和为30.59，消耗总功率为24.92 kW，耗时0.69 s。可以看出，MSWOA分配结果总体上要优于传统的SQP推力分配方法，特别是期望值发生较大跃变时，SQP需要更长时间恢复稳定输出。

3）仿真实例3

本实例进行随机波动动态测试，测试参数设置与实例2相同，仿真处理结果如表5、图3所示。

由表5可知，实例3情况下，本文算法优化结果不但耗时更低，而且偏差和功率都最低，具备较强的稳定收敛性；PSO和WOA也取得了较好的分配效果，但稳定性稍差；SSA和WOA1两种算法在较少迭代次数的情况下寻优效果依然不理想，稳定性差，但SSA稍强于WOA1。本实例进一步表明个体变量采用MSWOA更有利于获取最优解。图3中SQP算法绝对误差和为91.14，消耗总功率为18.94 kW，耗时1.31 s。可以看出，该算法寻优结果比表中大部分群智能算法都差，除了耗时具有较大优势，然而群智能算法运行时间能满足一定的工程应用需求。

5 结束语

为了提高鲸鱼优化算法在船舶推力分配应用中的精度以及快速稳定收敛性，本文设计了一种多策略鲸鱼推力分配算法。通过实例分析表明，本文提出的个体变量选择方式由于满足严格等式约束条件，且涵盖此条件下所有的可行解，其更加科学合理；提出的空间区块化和“精英”筛选种群初始化方法，提高了初始种群的分散性并“精英”化，提高了算法全局收敛能力、降低了初始化对寻优结果的影响；所构建的动态个体边界机制实现了精准的空间寻优，提高了算法寻优效率；类梯度法的个体更新策略加强了个体区域寻优能力，是提高算法收敛稳定性的关键。仿真结果也表明，本文算法解决了实时收敛性问题，有利于实现节能减排，提高了推力分配的效果，具有良好的应用前景和推广价值。今后将进一步对类梯度法进行变步长和动态个体变量选择研究，以提高算法寻优效果。

参考文献：

［1］陈荣旗. 海洋油气生产装备智能制造发展现状及前景展望［J］.中国海上油气， 2020，32（4）： 152-157. （Chen Rongqi. Current development status and prospects of the intelligent manufacturing of offshore oil and gas production equipment［J］. China Offshore Oil and Gas， 2020，32（4）： 152-157.）

［2］Morgan M J. 近海船舶的动力定位［M］. 耿慧彬，译. 北京：国防工业出版社， 1984： 188-200. （Morgan M J. Dynamic positioning system of offshore ships［M］. Geng Huibin， Trans. Beijing：National Defense Industry Press， 1984： 188-200.）

［3］陈亚豪，徐海祥，李文娟，等. 能量最优组合偏置推力分配算法［J］.大连海事大学学报， 2019，45（1）： 26-32. （Chen Yahao， Xu Haixiang， Li Wenjuan， et al. Energy optimal combined bias thrust allocation algorithm［J］. Journal of Dalian Maritime University， 2019，45（1）：26-32.）

［4］Wichers J， Bultema S， Matten R. Hydrodynamic research on and optimizing dynamic positioning system of a deep water drilling vessel［C］//Proc of the 30th Offshore Technology Conference.［S.l.］： OnePetro， 1998：553-564.

［5］李新飛，马强，袁利毫，等. 作业型ROV矢量推进建模及推力分配方法［J］. 船舶力学， 2020，24（3）： 332-341. （Li Xinfei， Ma Qiang， Yuan Lihao， et al. Vector propelling system model and thrust allocation for work-class ROV［J］. Journal of Ship Mechanics， 2020，24（3）： 332-341.）

［6］Sordalen O J. Optimal thrust allocation for marine vessels［J］. Control Engineering Practice， 1997，5（9）： 1223-1231.

［7］Arditti F， Cozijn H， Daalen E V， et al. Robust thrust allocation algorithm considering hydrodynamic interactions and actuator physical limitations［J］. Journal of Marine Science and Technology， 2019，24（1）： 1057-1070.

［8］Tang Ziying， He Huacheng， Wang Lei， et al. An optimal thrust allocation algorithm with bivariate thrust efficiency function considering hydrodynamic interactions［J］. Journal of Marine Science and Technology， 2021， 27（1）： 52-66.

［9］赵伟， 刘焕卫. 基于严格等式约束的推力分配算法研究［J］. 船舶力学， 2021，25（4）： 443-452. （Zhao Wei， Liu Huanwei. Research on thrust allocation algorithm based on strict equality constrain［J］. Journal of Ship Mechanics， 2021， 25（4）： 443-452.）

［10］Gao Diju， Wang Xuyang， Wang Tianzhen， et al. Optimal thrust allocation strategy of electric propulsion ship based on improved non-dominated sorting genetic algorithm Ⅱ［J］. IEEE Access， 2019， 7： 135247-135255.

［11］梁海志，乔东生，李芦钰，等. 基于遗传算法的半潜式平台动力定位系统动态约束可行域推力分配法［J］.船舶力学， 2018， 22（10）： 1224-1232. （Liang Haizhi， Qiao Dongsheng， Li Luyu， et al. Dynamic positioning system thrust allocation of semi-submersible platform based on dynamical constraint allocation method［J］. Journal of Ship Mechanics， 2018， 22（10）： 1224-1232.）

［12］尚留宾，王威，刘志华. 基于粒子群算法的动力定位推力分配决策变量优选［J］. 船舶工程， 2019，41（10）： 81-84，91. （Shang Liubin， Wang wei， Liu Zhihua. Optimization of decision variables for dynamic positioning thrust distribution based on particle swarm optimization［J］. Ship Engineering， 2019， 41（10）： 81-84，91.）

［13］李新想，王锡淮，肖健梅. 基于遗传混沌粒子群混合算法的船舶动力定位推力分配研究［J］. 舰船科学技术， 2018，40（12）： 99-103. （Li Xinxiang， Wang Xihuai， Xiao Jianmei. Research on thrust allocation of ship dynamic positioning based on genetic chaos particle swarm optimization algorithm［J］. Ship Science and Technology， 2018， 40（12）： 99-103.）

［14］卞顯洋，肖健梅. 基于改进混合蛙跳算法的船舶推力分配［J］. 船电技术， 2021，41（11）： 31-35. （Bian Xianyang， Xiao Jianmei. Ship thrust allocation based on improved shuffled frog leaping algorithm［J］. Marine Electric & Electronic Engineering， 2021，41（11）： 31-35.）

［15］Wu Defeng， Ren Fengkun， Zhang Weidong. An energy optimal thrust allocation method for the marine dynamic positioning system based on adaptive hybrid artificial bee colony algorithm［J］. Ocean Enginee-ring， 2016， 118（5）： 216-226.

［16］朱昱雯，肖健梅，王锡淮. 基于改进SHADE算法的船舶电力系统推力分配［J］. 中国舰船研究， 2020，15（4）： 173-182. （Zhu Yuwen， Xiao Jianmei， Wang Xihuai. Thrust distribution of marine power system based on improved SHADE algorithm［J］. Chinese Journal of Ship Research， 2020， 15（4）： 173-182.）

［17］黄炜. 基于改进人工鱼群算法的动力定位系统推力分配研究［D］.哈尔滨：哈尔滨工程大学， 2016. （Huang Wei. Research on thrust allocation of dynamic positioning system based on improved artificial fish swarm algorithm［D］. Harbin： Harbin Engineering University， 2018.）

［18］徐海祥， 文武， 冯辉. 自适应组合偏置推力分配算法［J］. 武汉理工大学学报， 2016，40（4）： 569-573. （Xu Haixiang， Wen Wu， Feng Hui. Adaptive group biasing thrust allocation algorithm［J］. Journal of Wuhan University of Technology， 2016， 40（4）： 569-573.）

［19］董海， 吴瑶. 电网中断下基于DWOA的生鲜产品闭环供应链网络多目标模糊优化设计［J］. 计算机应用研究， 2021，38（6）： 1694-1698，1703. （Dong Hai， Wu Yao. Closed loop supply chain of fresh products based on DWOA under power grid interruption network multi-objective fuzzy optimization design［J］. Application Research of Computers， 2021，38（6）： 1694-1698，1703.）

［20］孙琪， 于永进， 王玉彬， 等. 采用改进鲸鱼算法的配电网综合优化［J］.电力系统及其自动化学报， 2021，33（5）： 22-29. （Sun Qi， Yu Yongjin， Wang Yubin， et al. Comprehensive optimization of distribution network using improved whale optimization algorithm［J］. Proceedings of the CSU-EPSA， 2021，33（5）： 22-29.）

［21］郝曉弘， 宋吉祥， 周强， 等. 混合策略改进的鲸鱼优化算法［J］. 计算机应用研究， 2020，37（12）： 3622-3626，3655. （Hao Xiaohong， Song Jixiang， Zhou Qiang， et al. Improved whale optimization algorithm based on hybrid strategy［J］. Application Research of Computers， 2020，37（12）： 3622-3626，3655.）

［22］武泽权， 牟永敏. 一种改进的鲸鱼优化算法［J］. 计算机应用研究， 2020，37（12）： 3618-3621. （Wu Zequan， Mu Yongmin. Improved whale optimization algorithm［J］. Application Research of Computers， 2020，37（12）： 3618-3621.）