基于混沌反向学习和水波算法改进的白鲸优化算法
2024-05-24王亚辉张虎晨王学兵胡继明李娅
王亚辉 张虎晨 王学兵 胡继明 李娅

摘 要:针对原始的白鲸算法(beluga whale optimization,BWO)在某些情况下,中后期的探索和开发能力不足、多样性和求解精度降低、容易陷入局部最优等问题,提出一种基于混沌反向学习和水波算法改进的白鲸优化算法(TWBWO),进一步提高白鲸算法的计算精度和收敛速度,增强全局搜索和跳出局部最优能力。结合混沌映射和反向学习策略提高种群的质量和多样性,加快收敛速度。引入水波算法(water wave optimization,WWO)的折射操作,避免寻优时轻易陷入局部最优,提高计算精度。实验结果表明,TWBWO算法较之原始算法和其他经典算法在收敛速度和求解精度以及稳定性方面更为优秀,性能和寻优能力更强。
关键词:白鲸优化算法; 水波算法; 混沌映射; 反向学习; 算法改进
中图分类号:TP301 文献标志码:A
文章编号:1001-3695(2024)03-013-0729-07
doi:10.19734/j.issn.1001-3695.2023.07.0332
Improved beluga whale optimization algorithm based onchaotic inverse learning and water wave algorithm
Wang Yahui, Zhang Huchen, Wang Xuebing, Hu Jiming, Li Ya
(College of Mechanical, North China University of Water Resources & Electric Power, Zhengzhou 450045, China)
Abstract:To address the problems of the original BWO algorithm,such as insufficient exploration and exploitation ability in the middle and late stages in some cases, reduce the diversity and solution accuracy, easy to fall into local optimality,this paper proposed a white whale optimization algorithm (TWBWO) based on chaotic backward learning and water wave algorithm improvement. Further it improved the computational accuracy and convergence speed of Moby Dick algorithm, enhanced the ability of global search and jumping out of local optimum. Combining chaotic mapping and backward learning strategies,it improved the quality and diversity of populations and speeded up the convergence rate. It introduced the refraction operation of the WWO to avoid the algorithm from repeatedly falling into local optima and improve the computational accuracy. The experimental results show that the TWBWO algorithm is superior to the original algorithm and other classical algorithms in terms of convergence speed and solution accuracy as well as stability, with better performance and better finding ability.
Key words:BWO; WWO; chaotic mapping; reverse learning; algorithm improvement
0 引言
尋得问题的最佳处理方案一直是各学科的焦点,受自然界生物的启发,学者们提出了很多群智能优化算法来解决最优问题[1]。白鲸算法(BWO)是由Zhong等人[2]观察白鲸群体的生活行为后于2022年提出的一种元启发式优化算法,该算法具有结构设计简单、收敛速度快、求解精度高等优点。黄欣等人[3]使用白鲸算法优化密度聚类算法(density-based spatial clustering of applications with noise,DBSCAN)实现全局参数的自适应选取,提升了效率和聚类结果的可信度,并应用于变电站数据流异常检测。Houssein等人[4]将动态候选解(dynamic candidate solutions,DCS)和K-最近邻(K-nearest neighbor,KNN)分类器结合,通过给潜在候选者一个机会,提高了选择解的多样性和一致性。蔡海良等人[5]利用白鲸算法优化极限学习机(extreme learning machine,ELM)初始参数,用于电力光缆故障诊断及定位。
针对传统白鲸算法在一些情况下多样性和求解精度降低、容易陷入局部最优等问题,本文提出一种基于混沌反向学习和水波算法(WWO)改进的白鲸算法(TWBWO)。混沌映射和反向学习用于前期的种群初始化来提升种群的质量和多样性,加快收敛速度。引入水波算法的折射理念,折射当前迭代寻到的最优解,提高计算精度,避免陷入局部最优。通过多组测试函数、多维度、多算法进行对比实验。结果表明,改进后的算法较原始算法性能有明显提升。
1 原始白鲸优化算法(BWO)
BWO算法是通过观察白鲸生活行为提出的元启发式算法,如图1所示。
1.1 初始化
基于白鲸种群的机制,白鲸被视为搜索代理,每条白鲸都代表一个候选方案,在优化过程中不断更新,其模型被建立为
2.2 水波算法(WWO)
Zheng受浅水波理论的启发,模拟水波运动中的传播、折射、碎浪运动,于2015年提出了水波优化算法(WWO)[14]。该算法中水波的适应度值与海底深度和波长成反比,距离静止水位越近,适应度值越高,波长越短[15]。通过波长控制水波的搜索范围,适应度低的水波进行大范围的搜索,最大可能尋找更优解,适应度高的水波进行小范围局部搜索,保证解的质量,如图4[16]所示。
每一次迭代,种群中首先会进行传播操作,水波个体x通过在每一维d上增加随机的位移来产生新的个体解[17]。每次的传播操作更新波长之后会衰减水波个体的波高,当波高逐渐降低为0时,算法进入折射操作,使其向当前最优个体学习,避免算法停滞[18]。在搜索到新的最优水波后进行碎浪操作,并将其分解,进行更细致的局部搜索,保证解的优越性。
为了提升BWO算法跳出局部最优的能力,提高收敛速度与计算精度,将WWO与BWO算法结合。在BWO算法寻到当前全局最优解后,引入折射操作,对最优解进行折射学习,对比新个体与当前最优个体适应度值,选择优值替代进入下一次迭代。改进后公式如下:
Xd=N(Xbest+Xm2,|Xbest-Xm|2)(14)
Xm=mean(Xbest+Xworst)(15)
其中:Xbest、Xworst分别为当前种群中最优和最差个体;Xm是两者的平均位置;N(μ,σ)是均值为μ、标准差为σ的高斯随机数。
图5为水波算法优化后的BWO算法与原始BWO算法在同一测试函数上的迭代曲线对比。可以看出,结合水波算法后,白鲸算法跳出局部最优的能力明显提升,加快了收敛速度,提升了计算精度。
2.3 TWBWO算法
混沌反向学习和水波算法都能对白鲸算法进行有效的优化,在一定程度上提升算法性能,但两者各自所优化BWO算法的方式并不冲突且互不影响。混沌反向学习策略优化BWO算法的初始化阶段,提升种群质量。水波算法影响的是勘探、开发、鲸落阶段的当前最优值。因此,将两者互补结合,进一步提升BWO算法的性能。在同一测试函数上的实验对比结果如图6所示。可以看出,TWBWO算法充分继承了前两者的优点,进一步提升了BWO算法的性能。
TWBWO算法流程如图7所示。TWBWO算法实现步骤如下:
a)对参数P、dim、lb、ub、T进行初始化,P为种群中个体数量,dim为个体维度,lb、ub为解的下限和上限,T为最大迭代次数。
b)使用混沌反向学习策略进行初始化,获得新的初始种群,检验是否超出搜索边界,计算适应度值并排序,得到当前最优个体解和最差个体解。
c)根据式(3)(10)计算平衡因子Bf和鲸落概率Wf。
d)如果Bf<0.5,进入开发阶段,按照式(5)更新个体位置;如果Bf>0.5,进入勘探阶段,按照式(4)更新个体位置。
e)在步骤c)d)结束后,对比平衡因子Bf和鲸落概率Wf。若Bf
f)在所有个体经历过一次迭代后,计算适应度值,找出新的当前最优解和最差解,根据式(14)(15)对最优解进行折射操作,计算适应度值并对比保存最优解。
g)判断是否满足最大迭代次数或停止条件,不满足则返回步骤c),直至满足后输出最终结果。
3 实验与分析
3.1 实验设计
选择十个基准测试函数进行实验,测试改进算法的性能。同时,为对比TWBWO算法的优越性,将其与原始白鲸算法(BWO)、鲸鱼算法(whale optimization algorithm,WOA)[19]、灰狼算法(grey wolf optimizer,GWO)[20]、混合蛙跳算法(grey wolf optimizer,SFLA)[21]、果蝇算法(fruit fly optimization algorithm,FOA)[22]进行对比实验。实验中种群规模为50,最多迭代100次,分别进行30次独立实验。测试函数如表1所示。
表1给出了测试函数的表达式、维度、范围以及理论最优值,其中F1~F4为单模态测试函数,用于测试算法是否能快速搜寻到最优解;F5~F10为多模态测试函数,用于测试算法能否有效跳出局部最优[23]。为了更好地体现算法在不同维度上的性能,将测试函数的维度分别设置为30、100、500维。
3.2 实验结果
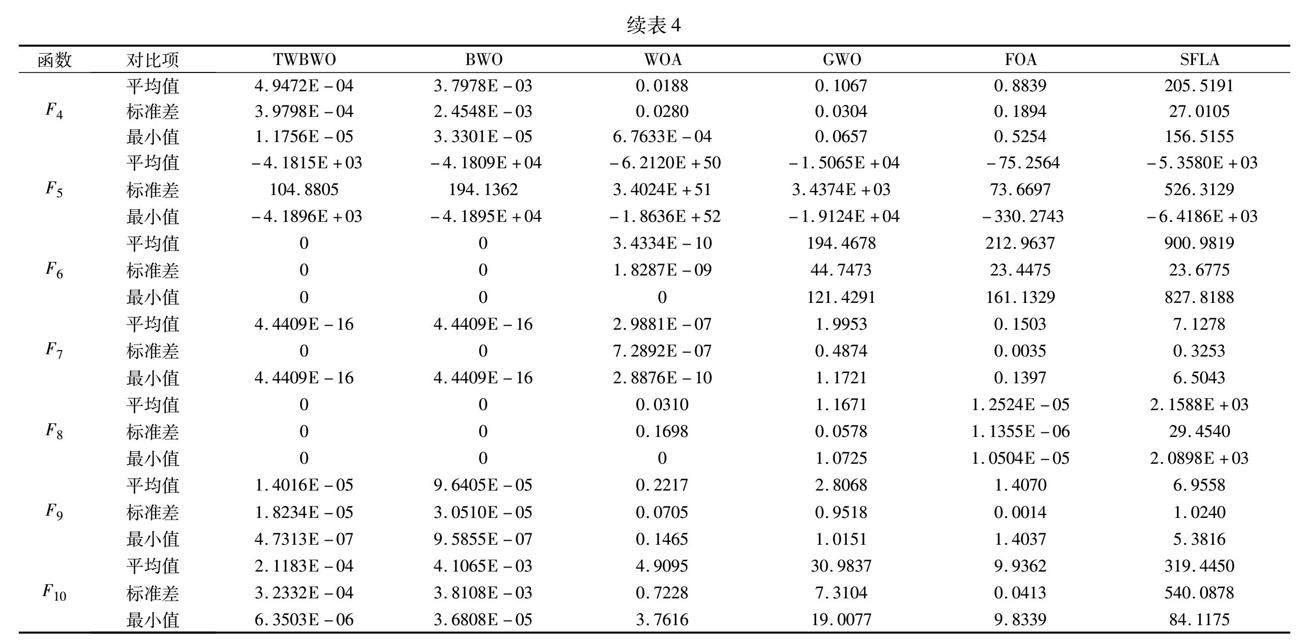
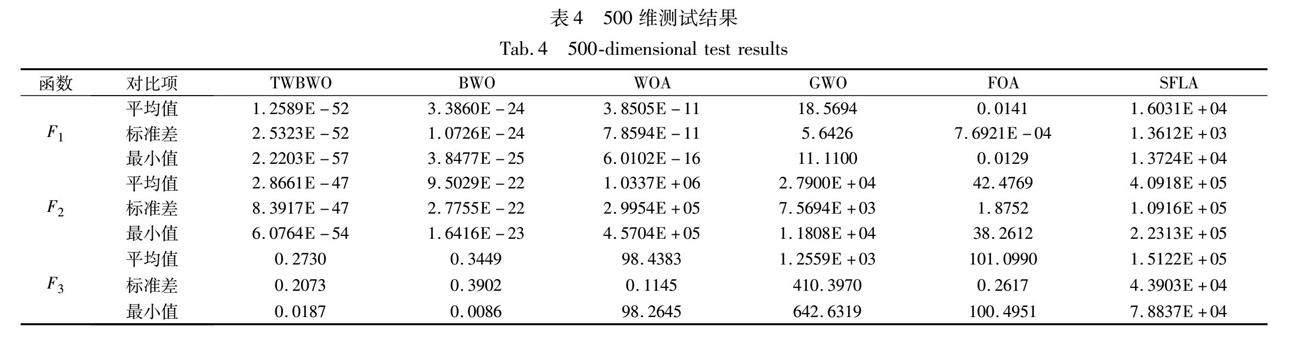
表2~4分别列出了TWBWO、BWO、WOA、GWO、FOA和SFLA算法在十个测试函数的30、100、500维度上独立运行30次,每次迭代100步的实验结果。实验结果统计了每个算法运行30次的最优值(best)、平均值(mean)、标准差(std),在寻找最优解的问题中,平均值越小表明算法寻优精度越高,而标准差越小则证明算法越稳定[24]。
由表中结果可知,通过平均值的比较,无论是在4个单模态测试函数,还是6个多模态测试函数中,TWBWO算法在寻优精度上都表现出了更好的性能,证明结合水波算法的折射操作可以有效提升白鲸算法的局部搜索能力。通过标准差的比较,验证了TWBWO算法的稳定性更好。而在面对高维问题时,求解过程更加复杂,算法寻找最优解的难度不断提升,TWBWO算法仍保持较高的寻优精度和鲁棒性,较之其他算法更加稳定。
为了验证TWBWO算法在收敛速度方面的性能,针对本文使用的十个测试函数,选择寻优维度为30,以迭代次数为x轴,适应度值为y轴,绘制TWBWO、BWO、WOA、GWO、FOA、SFLA六个算法的迭代曲线进行对比[25],如图8所示。
在十个测试函数中,TWBWO算法的收敛速度明显优于其他算法。在单模态测试函数中,TWBWO算法在函数F1、F2明显收敛更快,虽无法收敛,但得到的最终结果在10-40上下,已无限接近最优解。函数F3未在100次迭代后收敛,但相较其他算法,在都无法收敛的情况下,前期搜索效率更高、速度更快且更接近最优解。在多模态测试函数中,TWBWO算法只需20次迭代便可在函数F5收敛得到最優解,且精度最好,更是只需38次迭代和42次迭代便得到了函数F6和F8的理论最优解,在函数F7、F9、F10的收敛速度也都有明显提高。
通过混沌反向学习策略加强了初始种群的质量和多样性,使得算法一开始便能找到优秀的初始值,在迭代初期就有较高的精度。折射操作的存在也能保证算法不会重复陷入局部最优,加快收敛速度。这使得TWBWO算法在收敛速度和寻优精度上都具有明显的优越性。
稳定性是评价算法优劣的一个重要因素,为了验证TWBWO算法的稳定性,对TWBWO算法和五个对比算法在F3测试函数上进行30次独立实验,收集实验结果并绘制箱型图,结果如图9所示。从箱型图可以看出,TWBWO算法30次独立实验所得到的最优值分布基本在一条直线上,相比于BWO算法分布波动更小、更均匀,对比另外四个算法更是有着巨大的优势,证明TWBWO算法具有更为优越的稳定性。
4 结束语
针对原始白鲸算法在某些情况下,中后期的探索和开发能力不足、多样性和求解精度降低、容易陷入局部最优等问题,提出一种基于混沌反向学习和水波算法改进的白鲸优化算法(TWBWO)来提高计算精度和收敛速度,增强全局搜索和跳出局部最优的能力。算法初期通过混沌映射和反向学习策略初始化种群,提高种群的质量和多样性,提高初始解的质量。引入水波算法(WWO)的折射操作对每次迭代得到的最优解进行折射,增强算法跳出局部最优的能力,提高算法的计算精度,进一步提升算法的寻优性能。
实验结果表明,即使在高维情况下,TWBWO算法在收敛速度和求解精度以及稳定性方面都更为优秀,寻优性能更强。相较于提高初始种群质量和折射当前最优解来提高算法性能,如何改进算法的勘探阶段和开发阶段进一步提升算法性能,是下一步工作研究的重点。
图9 F3最优解分布箱型图
Fig.9 Box plot of F3 optimal solution distribution
参考文献:
[1]Ouyang Weimin, Ramachandran V. Classroom education effect evaluation model based on MFO intelligent optimization algorithm[J]. Journal of Intelligent & Fuzzy Systems, 2021,40(4) : 6791-6802.
[2]Zhong Changting, Li Gang, Meng Zeng. Beluga whale optimization: a novel nature-inspired metaheuristic algorithm[J]. Knowledge-Based Systems, 2022,251: article No.109215.
[3]黄欣, 赵敏彤, 郇嘉嘉, 等. 基于BWO-DBSCAN和CSA-OCRKELM的变电站数据流异常检测方法[J]. 广东电力, 2023,36(5): 39-48. (Huang Xin, Zhao Mintong, Jun Jiajia, et al. A substation data flow anomaly detection method based on BWO-DBSCAN and CSA-OCRKELM[J]. Guangdong Electric Power, 2023,36(5): 39-48.)
[4]Houssein E H. Sayed A. Dynamic candidate solution boosted beluga whale optimization algorithm for biomedical classification[J]. Mathematics, 2023,11(3): article No.707.
[5]蔡海良, 胡凯, 李军, 等. 基于BWO-ELM算法与VR-GIS技术的电力光缆故障诊断及定位研究[J]. 计算机测量与制, 2022, 30(12): 98-104,111. (Cai Hailiang, Hu Kai, Li Jun, et al. Research on power fiber optic cable fault diagnosis and localization based on BWO-ELM algorithm and VR-GIS technology[J]. Computer Measurement and System, 2022,30(12): 98-104,111.
[6]Ma Denglong, Tan Wei, Wang Qingsheng, et al. Application and improvement of swarm intelligence optimization algorithm in gas emission source identification in atmosphere[J]. Journal of Loss Prevention in the Process Industries, 2018,56: 262-271.
[7]Zhang Jinghua, Dong Ze. A general intelligent optimization algorithm combination framework with application in economic load dispatch problems[J]. Energies, 2019,12(11): article No.2175.
[8]Gurses D, Pholdee N, Bureerat S, et al. A novel hybrid water wave optimization algorithm for solving complex constrained engineering problems[J]. Materials Testing, 2021,63(6):560-564.
[9]Yin Qiang, Cao Ben, Li Xue,et al. An intelligent optimization algorithm for constructing a DNA storage code: NOL-HHO[J]. International Journal of Molecular Sciences, 2020,21(6) : article No.2191.
[10]Cui Fan, Ni Jianyu, Du Yunfei, et al. Soil water content estimation using ground penetrating radar data via group intelligence optimization algorithms: an application in the northern shaanxi coal mining area[J]. Energy Exploration & Exploitation, 2021,39(1): 318-335.
[11]Nie Xin, Luo Jian. The hybrid intelligent optimization algorithm and multi-objective optimization based on big data[J]. Journal of Phy-sics: Conference Series, 2021,1757(1) : article No.012132.
[12]Hu Shanshan, Liu Hui, Feng Yufei, et al. Tool wear prediction in glass fiber reinforced polymer small-hole drilling based on an improved circle chaotic mapping grey wolf algorithm for BP neural network[J]. Applied Sciences, 2023,13(5): article No.2811.
[13]Huang Yujie, Li Yibing, Zhang Zitang, et al. A novel path planning approach for AUV based on improved whale optimization algorithm using segment learning and adaptive operator selection[J]. Ocean Engineering, 2023,280: article No.114591.
[14]付接遞. 鲸鱼优化算法改进与应用研究[D]. 银川:宁夏大学, 2022. (Fu Jiedi. Research on the improvement and application of whale optimization algorithm[D]. Yinchuan:Ningxia University, 2022.)
[15]Sun Yulong, Li Hongjuan, Shabaz M,et al. Research on building truss design based on particle swarm intelligence optimization algorithm[J]. International Journal of System Assurance Enginee-ring and Management, 2021,13: 38-48.
[16]Azam A, Bardhan A, Kaloop M R, et al. Modeling resilient modulus of subgrade soils using LSSVM optimized with swarm intelligence algorithms[J]. Scientific Reports, 2022,12: article No.14454.
[17]Ozbay F A. A modified seahorse optimization algorithm based on chao-tic maps for solving global optimization and engineering problems[J]. Engineering Science and Technology, an International Journal, 2023,41: 1-26.
[18]Zhang Danfeng, Han Congai, Zhang Haiyan, et al. The simulation design of microwave absorption performance for the multi-layered carbon-based nanocomposites using intelligent optimization algorithm[J]. Nanomaterials, 2021,11(8): article No.1951.
[19]Li Yuzhou, Sun Chuanxia, Hu Yinglei. Whale optimization algorithm-based deep learning model for driver identification in intelligent transport systems[J]. Computers, Materials & Continua, 2023,75(2):3497-3515.
[20]Lambrinidis G, Tsantili-Kakoulidou A. Multi-objective optimization methods in novel drug design[J]. Expert Opinion on Drug Disco-very, 2021,16(6): 647-658.
[21]Zhang Meilun, Zhang Jin, Xu Maoda, et al. Improved SFLA algorithm with hybrid SA strategy for multi-objective reactive power planning optimization of distribution network[J]. Journal of Physics: Conference Series, 2021,1865(4) : article No.042056.
[22]Yonghua Bai, Minzhou Luo, Pang Fenglin. An algorithm for solving robot inverse kinematics based on FOA optimized BP neural network[J]. Applied Sciences, 2021,11(15): article No.7129.
[23]Jiang Wenjun, Zhang Ning. Research on characteristics of paper-plastic composite film based on intelligent optimization algorithm[J]. Personal and Ubiquitous Computing, 2021,25(S1): article No.27.
[24]Zhang Junrong, Tang Huiming, Tannant D D, et al. A novel model for landslide displacement prediction based on EDR selection and multi-swarm intelligence optimization algorithm[J]. Sensors, 2021,21(24): article No.8352.
[25]Shokouhandeh H, Kamarposhti M, Holderbaum W, et al. Optimal operation of distributed generations considering demand response in a microgrid using GWO algorithm[J]. Computer Systems Science and Engineering, 2023,47(1):809-822.
