复杂数据流在线集成分类算法综述

李春鹏 韩萌 孟凡兴 何菲菲 张瑞华

摘 要：复杂数据流中所存在的概念漂移及不平衡问题降低了分类器的性能。传统的批量学习算法需要考虑内存以及运行时间等因素，在快速到达的海量数据流中性能并不突出，并且其中还包含着大量的漂移及类失衡现象，利用在线集成算法处理复杂数据流问题已经成为数据挖掘领域重要的研究课题。从集成策略的角度对bagging、boosting、stacking集成方法的在线版本进行了介绍与总结，并对比了不同模型之间的性能。首次对复杂数据流的在线集成分类算法进行了详细的总结与分析，从主动检测和被动自适应两个方面对概念漂移数据流检测与分类算法进行了介绍，从数据预处理和代价敏感两个方面介绍不平衡数据流，并分析了代表性算法的时空效率，之后对使用相同数据集的算法性能进行了对比。最后，针对复杂数据流在线集成分类研究领域的挑战提出了下一步研究方向。

关键词：在线学习；集成学习；概念漂移；不平衡

中图分类号：TP391   文献标志码：A

文章编号：1001-3695（2024）03-001-0641-11

doi：10.19734/j.issn.1001-3695.2023.06.0291

Survey of online ensemble classification algorithms for complex data streams

Li Chunpeng，Han Meng，Meng Fanxing，He Feifei，Zhang Ruihua

（School of Computer Science & Engineering，North Minzu University，Yinchuan 750021，China）

Abstract：The concept drift and imbalance problems in complex data streams reduce the performance of classifiers.Traditional batch learning algorithms need to consider factors such as memory and runtime，but their performance is not outstanding in ra-pidly arriving massive data streams，and they also contain a large number of drift and class imbalance phenomena.Utilizing online ensemble algorithms to handle complex data stream problems has become an important research topic in the field of data mining.Firstly，this paper introduced and summarized the online versions of bagging，boosting，and stacking ensemble methods from the perspective of ensemble strategies，and compared the performance of different models.Secondly，this paper conducted a detailed summary and analysis of online ensemble classification algorithms for complex data streams for the first time.This paper introduced conceptual drift data stream detection and classification algorithms from two aspects：active detection and passive adaptation.This paper introduced unbalanced data streams from two aspects：data preprocessing and cost sensitivity.This paper analyzed the spatiotemporal efficiency of representative algorithms，and then compared the performance of algorithms using the same dataset.Finally，this paper proposed the next research direction in response to the challenges in the field of online ensemble classification of complex data streams.

Key words：online learning；ensemble learning；concept drift；imbalance

0 引言

現代数据有两个关键特征：无限到达的数据、不断增长的速度以及不断变化的数据性质，这两个因素的结合产生了数据流的概念。数据流会随着时间的推移而演变，其特征和定义也会发生变化，此外，数据流的初始分布可能会呈现出极不平衡的状态。复杂数据流中所存在的这两种现象分别被称为概念漂移和类不平衡，目前已成为数据流学习中的关键问题。风险管理［1］、异常检测［2］和社交媒体挖掘［3］等各个领域的应用都受到概念漂移和类不平衡的影响。传统的批量学习方法（如ID3、C4.5等经典决策树算法）在学习海量数据流时存在内存存储问题，并且无法根据新实例在旧模型的基础上进行增量更新。而在线学习［4］用于对按顺序到达的数据进行学习，无须将整个数据保存在内存中，这种方法适用于挖掘高速生成的大量数据。

集成方法［5］通过将多个弱分类器组合成一个较强的分类器，往往能够取得比单个分类器更好的性能。在数据流集成分类领域中，集成方法通常可分为基于块的集成和在线集成。基于块的模型在处理时变数据流时适应性较差，而在线模型则在准确度和内存等方面具有显著优势。在线集成方法因其良好的时空效率和预测性能而得到研究人员的广泛关注，图1给出了在线集成分类模型的概述图。Oza等人［6］将批量模式下的bagging和boosting算法推广到在线版本，在测试大量连续到达的数据流时表现良好，非常适合实际应用。Santos等人［7］基于在线boosting算法并进行改进，增加对困难分类实例的关注并根据当前分类器的预测结果动态选择后续分类器，加快了集成模型从概念漂移中恢复的速度。Wang等人［8］将重采样技术与在线bagging算法结合起来，并通过动态捕捉失衡率对数据进行再平衡，以解决数据流中的类不平衡问题。

在现有的数据流集成分类研究成果中，大多数综述都集中在集成学习或在线学习方面进行研究。Gomes等人［9］基于多样性、基分类器和集成方式的不同来总结集成相关技术。杜诗语等人［10］重点分析了突变型、渐变型、重复型和增量型概念漂移集成分类算法。张喜龙等人［11］ 从复杂数据流和领域数据流的角度重点介绍了当前算法的核心思想和性能。Mienye等人［12］总结了bagging、boosting和stacking三种主要的集成方法，并总结了它们的数学和算法表示。Hoi等人［4］基于模型对学习器的反馈类型对在线学习算法进行了分类总结。文献［13］介绍了在线学习的基本框架和性能评估方法。在目前的研究中，还未有对复杂数据流的在线集成分类方法进行介绍的综述。

本文对近年来所提出的在线集成分类方法进行了汇总，然后从集成策略的不同以及针对不同数据流对象所应用的集成技术对在线集成分类算法进行了详细的描述和分析，本文的框架结构如图2所示，主要贡献如下：

a）首次对在线集成分类算法进行了详细的介绍，包括online bagging、online boosting及online stacking等经典模型及其最新变体，同时对提出模型进行总结与比较。

b）对概念漂移数据流及不平衡数据流的在线集成分类方法进行了详细的阐述与分析，并对代表性算法进行了时空复杂度的分析。

c）在使用同一数据集的条件下，对在线集成分类算法性能的实验结果进行了分析与对比。

1 在线集成策略

在线集成学习方法对新到达的实例逐个进行处理，是一种增量学习方法。装袋（bagging）、提升（boosting）和堆叠（stacking）等是改进单分类器性能的经典集成方法［12］，同时研究人员们也提出了它们的在线版本及变体，以适应不断变化的数据流。本章主要从集成策略的在线版本进行总结与比较。

1.1 bagging

标准的批量bagging方法是从原始样本集中进行抽样，通过N轮抽取得到相应的训练集，并通过训练得到N个模型。对于测试集的分类结果，由这些模型采用投票的方式来决定。最经典的在线bagging算法是Oza等人［6］提出的OzaBag算法，该算法通过泊松分布来模拟批量环境，首先将集成分类器中的基分类器数量设置为N。对于每个新到达的实例d，根据泊松分布k-poisson（1），然后重复以下过程k次：将样本d添加到训练集中，并用新的训练集更新所有的基分类器。最后，采用多数投票原则对新实例进行预测。OzaBag算法过程如图3所示。

2009年，Bifet等人［14］对OzaBag方法作出改進，提出了ADWIN bagging（ADWINBag）和自适应大小Hoeffding树bagging（ASHTBag）两种bagging变体。ADWINBag通过使用ADWIN作为漂移检测器来决定何时丢弃表现不佳的集合成员，当检测到漂移时，进行分类器的删除与替换。ASHTBag使用不同大小的Hoeffding树作为其组件分类器，同时利用 OzaBag 的重采样方法使得每棵树运行在不同的实例集合上，通过增加树的多样性来提高bagging集成的性能。2010年，Bifet等人［15］又基于OzaBag算法，提出了LevBag（leverage bagging），将bagging采样的泊松分布参数从固定值1改为较大的λ，从而增加了基分类器输入的随机性，以提高集成分类器的准确性。

近年来，随着机器学习技术的不断发展，研究人员将各种方法与在线bagging相结合以提高分类器集成的整体性能，来处理不同环境下的学习任务。SMOTE-OB［16］将在线bagging算法和SMOTE［17］合成少数过采样技术结合起来，通过使用随机特征子集及利用在线bagging泊松分布中的概率更新实例，使其基分类器多样化。进化模糊系统（EFS）［18］可以在在线过程中以增量的方式从动态数据中学习，Lughofer等人［19］结合EFS提出了一种新的自适应在线集成变体，称为在线袋装EFS（OB-EFS），并采用两种修剪策略对集成成员进行动态修剪，可以很好地处理渐进和循环漂移。

在使用bagging方法进行模型集成时，基模型可以是任意模型，当基模型为决策树时，集成模型即被称之为随机森林（random forest，RF），它是bagging的扩展变体。在线随机森林（online random forest，ORF）［20］通过连续在线bagging采样将新的子节点从父节点中分离出来，最终可以获得与传统RF相当的性能。王爱平等人［21］提出了一种增量式极端随机森林分类器（incremental extremely random forest，IERF），用于处理小样本数据流的在线学习问题。IERF算法通过 Gini系数来确定是否对当前叶节点进行分裂扩展，能够快速高效地完成分类器的增量构造。文献［22］提出了自适应随机森林（adaptive random forest，ARF），ARF是对经典随机森林算法的改编。ARF 基于在线bagging的重采样方法和自适应策略来应对不断变化的数据流。该策略对每棵树使用漂移监视器来跟踪警告和漂移，并用于集成替换。

在线bagging由于其弱分类器投票组合的简易性以及对新实例的泊松重采样理论，经常与其他数据重采样技术相结合，用于处理不平衡数据，详细的内容将在第2章进行描述。

1.2 boosting

传统的批量boosting算法与bagging算法类似，但不同于bagging的并行学习，boosting是一种序列化的集成方法。它通过迭代地训练一组弱分类器（例如决策树）来构建一个强分类器。在每次迭代中，boosting算法根据先前分类器的表现来调整样本的权重，将更多的关注放在分类错误的样本，逐步提高对难以分类的样本的预测准确性。OzaBoost［6］通过泊松分布参数确定实例的权重，该算法通过式（1）对实例权重进行调整。

λscm=λscm+λdλd←λd（N2λscm），correct

λswm=λswm+λdλd←λd（N2λswm），wrong（1）

其中：λd表示新实例d的权重；N表示目前为止训练的实例总数；λscm表示第m阶段正确分类的实例之和；λswm表示错误分类实例的和。最后通过分类器的错误率进行加权投票得到预测结果。随着新实例的到来不断调节弱分类器的参数，使分类正确率高的分类器有较高的权重。

OzaBoost基于累积权重分配实例，一些研究者基于此进一步提出了其他算法。基于自适应多样性的在线增强算法（adaptable diversity-based online boosting，ADOB）［7］，是OzaBoost的改进版本，ADOB相对于OzaBoost来说最值得关注的地方在于，它在处理每个实例之前根据准确度对分类器进行升序排序，并通过分类器的预测结果动态选择后续分类器。基于启发式修改的类boosting在线学习集成（boosting-like online learning ensemble，BOLE）［23］，是对ADOB算法的改进，该方法削弱了分类器的错误率阈值以使更多的分类器参与投票，并改变所使用的概念漂移检测方法，经实证研究在大多数测试情况下，准确性得到了提高。文献［24］提出了两个在线版本的boosting，第一个是基于AdaBoost的在线M1算法（OABM1），负责更新权重的函数被修改为类似于传统boosting中的相应函数。第二种方法名为基于AdaBoost在线M2算法（OABM2），旨在处理多类问题，因为基于AdaBoost M1的版本在此类场景中会受到限制。结果表明这两种方法在不同环境下均具有良好的性能。

由于基于累积权重的实例分配方案容易受到噪声等数据困难因素的影响而降低集成性能，所以基于分类器性能反馈的方案被研究者所提出。Baidari等人［25］在ADOB的基础上，提出了基于准确率加权多样性的在线提升（accuracy weighted diversity-based online boosting，AWDOB）方法，引入了一种加权方案，使用分类器的准确率为数据流中的当前实例分配当前分类器权重，这些改进和新定义的加权方案提高了集成的整体精度。最近，Honnikoll 等人［26］提出了平均错误率加权在线提升方法（mean error rate weighted online boosting，MWOB），该算法利用个体基分类器的平均错误率来实现实例的有效权重分布，而不是OzaBoost中基于弱分类器之前的累积权重，MWOB在实验数据集上均取得了最佳的预测性能。

在线boosting算法中最值得注意的地方就是如何对训练实例进行有效的权重分布，以达到良好的分类器性能。传统算法通过前件分类器的预测结果对实例进行相应的权重分配，但是这种方式很容易受到噪声影响。对于实例权重分配的研究一直是boosting集成中的一大热点。

1.3 stacking

stacking是集成学习的第三类，大部分集成模型如bagging、boosting都通过一个基础学习算法来生成同质的基学习器，即同构集成，而stacking为异构集成，基础模型通常包含不同的学习算法。stacking集成由两个级别组成：基分类器和元分类器（meta-classifier，通常为线性模型LR）。stacking的概念最初是由文献［27］提出的，基分类器采用k折交叉验证法将原始数据集分为训练集和测试集进行训练和预测。元分类器将基分类器集合在训练集上的预测值作为特征输入进行训练并生成模型，使用训练好的模型对由基分类器集合在测试集上的预测值所构建的特征数据集进行预测，得出最终的预测结果。图4展示了stacking集成的体系结构。

受限于stacking模型的训练过程，大多stacking算法及其变体都应用于批量环境，对于在线环境下的研究屈指可数，以下是本文对现有的在线 stacking算法的总结。Frías-Blanco 等人［28］提出了一种快速自适应堆叠集成（fast adaptive stacking of ensembles，FASE）方法，集成中包括一个用于稳定概念的主分类器。出现漂移警告时则训练一个备选分类器，若出现漂移确认，该分類器将取代主分类器，FASE能够在恒定的时间和空间计算复杂度下处理输入数据。FASE-AL［29］提出了对FASE算法的改进，该算法保持了其主要特性，使其能够处理只有小部分数据被标记的数据流。自适应堆叠集成模型（self-adaptive stacking ensemble model，SSEM）［30］选择性地集成不同的低复杂度、高多样性的基分类器，该文中选择了朴素贝叶斯（NB）、随机森林（RF）等五种最先进的分类器作为SSEM的基分类器，通过遗传算法自动选择最优基分类器组合以及组合的超参数。GOOWE-ML［31］是一种用于多标签分类的在线动态加权堆叠集成算法，该集成为分类器的相关性得分构建了一个空间模型，并使用该模型为其组件分类器分配最优权重，该模型可用于任何现有的增量多标签分类算法作为其基分类器。

1.4 小结

本章从bagging、boosting、stacking三种常用集成策略的在线版本及变体介绍了在线集成分类算法。通过现有研究的实验对比发现，一般的boosting模型在准确度方面并不优于bagging模型。潜在原因可能是：与bagging多数投票的简单方式不同，boosting算法根据基分类器的预测性能进行权重分配，这种方式在某些情况下的准确度较不稳定，且容易受到噪声的影响，从而对噪声数据进行不必要的训练，并在之后影响到基分类器的权重分配。而stacking模型用于提升预测结果，在整体上优于bagging模型以及boosting模型，但通常复杂度较高。

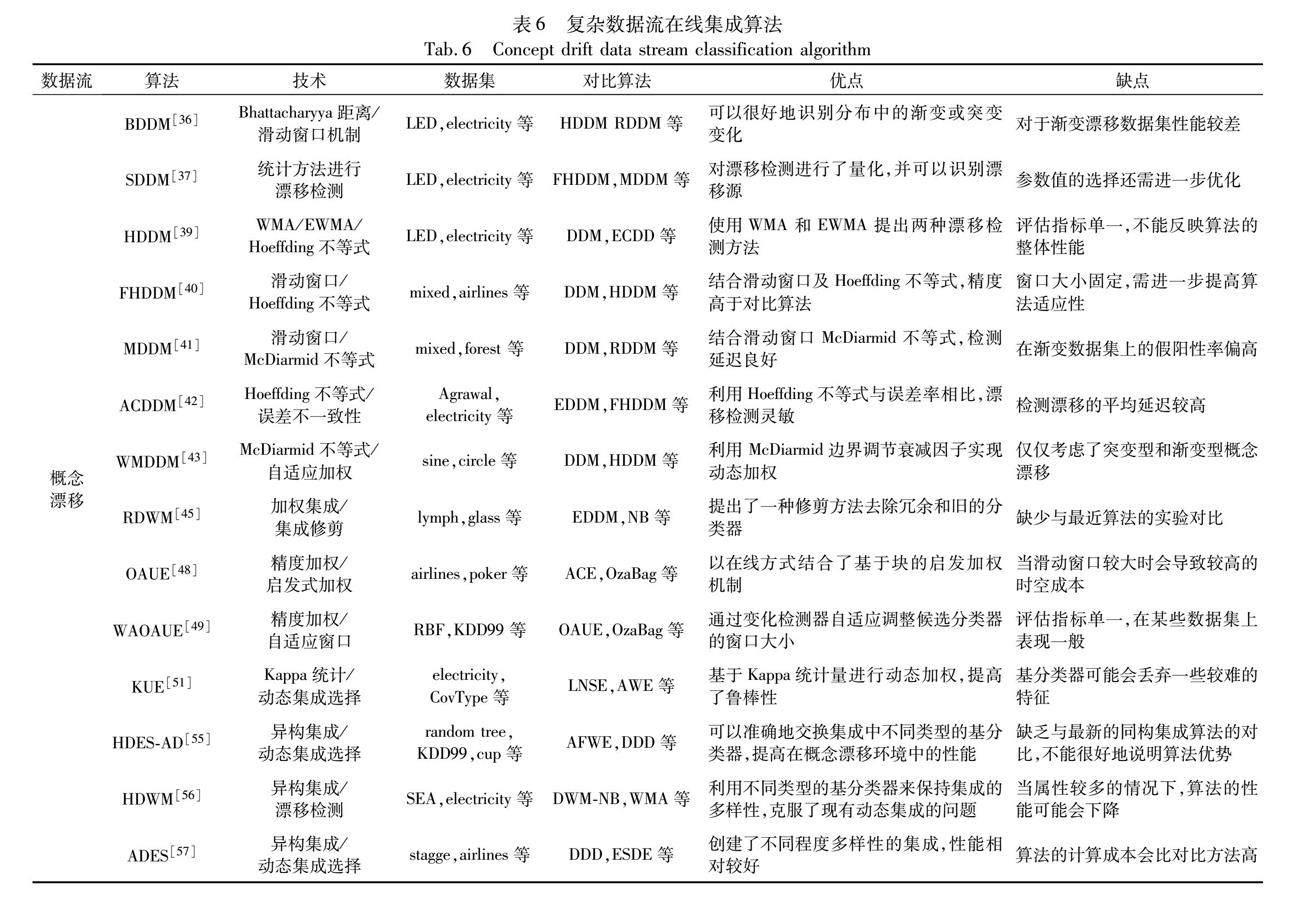
其中在LED合成数据集上，AdwinBag在准确率上居第一位，约为62%。ADOB、AdwinBoost、LevBag分别为59%、56%、61%，bagging模型整体上在准确率方面要优于一般的boosting模型约7%。而在真实数据集electricity中，最新的算法MWOB、AWDOB取得了最佳表现，分别为90%、93%，其次为LevBag、ADOB、AdwinBoost、AdwinBag，分别为90%、88%、87%、86%，这种情况可以解释为MWOB、AWDOB分别基于精度和平均错误率修改了错误分类实例的权重计算公式，而不是之前的累积权重，提升了boosting模型的整体稳定性。在credit card数据集上，stacking模型如SSEM算法在accuracy、recall、AUC、F-measure、MCC均表现最佳，分别为0.975、0.977、0.976、0.970以及0.968。图5从所用技术、对比算法和优缺点等方面对在线集成分类算法进行了总结。

2 复杂数据流在线集成分类技术

通常，数据流挖掘是指在快速到达的数据记录序列上执行的挖掘任务。由于收集数据的环境可能会动态变化，数据分布也可能相应变化，这种变化称为概念漂移。而初始的数据可能会呈现出巨大的差异，即类不平衡。这些对分类器的性能均造成了一定的影响，同时也得到了研究人员的广泛关注。

2.1 概念漂移数据流

在大数据时代背景下，概念漂移是一个非常重要的议题，因为数据类型和分布的不确定性是大数据的固有性质。在概念漂移数据流中，本文根据是否存在漂移检测机制，将在线集成学习方法分为基于主动检测的在线集成算法和基于被动自适应的在线集成算法［32］，并在下面的小节中进行展开。

2.1.1 基于主动检测的方法

主动方法通过监测数据流分类性能指标或者统计数据属性分布，并设置一个阈值用来判别是否发生了概念漂移，一旦检测到数据流中概念漂移的发生，算法将会采取重置学习模型等方法来适应数据流中新的概念。概念漂移的检测方式有多种，主要可分为基于统计的方法和基于窗口的方法。

1）基于统计的方法

基于统计的思想是比较数据分布之间的差异或者验证模型的误差是否在可控范围内，数据分布之间若存在着明显的差异则预示着概念漂移的发生，但在在线环境中通常无法提前得知数据的初始分布，所以在本小节中先讨论后者。因为在概念漂移环境中集成的性能会随着时间的推移而变化，当概念漂移发生时，性能会显著下降。如果模型达到了一定错误率，就会发送警报。最经典的算法漂移检测法（drift detecting method，DDM）［33］背后的思想是控制算法的在线错误率，当概率分布发生变化即发生概念漂移时，模型的错误率会上升。DDM估计t时间的错误率Pt及其标准差σt，标准差可定义为

σ=pt（1-pt）n（2）

DDM会为错误率设置两个阈值warning和drift：

pt+σt≥pmin+2σminwarning

pt+σt≥pmin+3σmindrift（3）

如果错误率到达了warning值，则发出漂移警报，若后续数据的到来没有让错误率降低并到达了drift，则确认发生概念漂移。DDM在突变漂移时性能良好，但是对于渐变型概念漂移的检测比较困难。早期漂移检测法（early drift detection method，EDDM）［34］以及反应性漂移检测方法（reactive drift detection method，RDDM）［35］等常用漂移检测方法都受到DDM的启发，并改良了DDM在渐变漂移时的性能损失问题。

在数据流学习算法中，数据分布的变化对于分类器的预测性能影响是巨大的，重点是学习模型需具备跟踪此变化的能力。Baidari等人［36］提出了一种基于Bhattacharyya距离的概念漂移检测方法（Bhattacharyya distance-based concept drift detection method，BDDM），该方法通过Bhattacharyya距离度量数据之间的差异，并使用单窗口用于从真实值序列中估计平均值和方差，以检测漂移。在实验中通过调节模型参数（窗口大小、差值和增量）达到了最佳性能，并在检测漂移时的延迟和误报率较对比算法更低。統计漂移检测方法（statistical drift detection method，SDDM）［37］同样也是通过检测数据分布的变化来检测概念漂移，不同的是其使用Kullback-Leibler散度作为距离度量，并通过参数化方法扩展了基线算法，SDDM不仅能够检测到漂移，更提供了漂移的可解释性。类似的距离度量还有Hellinger距离、总变异距离等，距离度量的选择取决于流的特性。

2）基于窗口的方法

基于窗口的模型主要关注时间戳和事件的发生，自适应滑动窗口（adaptive windowing，ADWIN）［38］是最具有代表性的基于窗口的检测方法，它保存了一个大小为W的滑动窗口用于存储最近实例，当检测到漂移时，W减小。同时还包含两个子窗口用来存储旧实例和新实例，当这两个子窗口的平均值之差高于给定阈值时，即报告漂移。近十年来，研究者将窗口模型和统计过程方法结合起来，提出了多种漂移检测方法。文献［39］提出了两种漂移检测方法，使用Hoeffding不等式作为平均值之间差值的上限。HDDMA-test比较滑动窗口的平均值以检测漂移，可用于检测突然漂移。HDDMW-test使用遗忘方案首先对移动平均线进行加权，然后进行比较以检测漂移，更适合检测增量漂移。Pesaranghader等人［40］提出的快速Hoeffding漂移检测方法（FHDDM）使用滑动窗口和Hoeffding不等式检测漂移点。与其他基于窗口的方法不同，该方法包含一个历史信息的窗口和另一个维护最新信息的窗口，使用单个滑动窗口将分类器精度与迄今为止观察到的最佳精度进行比较，当差值大于使用Hoeffding不等式确定的阈值时，发出漂移状态的信号。Pesaranghader等人［41］将McDiarmid不等式引入概念漂移检测，提出了McDiarmid漂移检测方法（McDiarmid drift detection method，MDDM），该算法通过对预测结果应用加权滑动窗口，最近的条目被赋予更高的权重。在实例处理过程中，将滑动窗口内元素的加权平均值与迄今为止观察到的最大加权平均值进行比较，若两者之间的差异大于McDiarmid不等式的上界，则意味着变化是显著的，即发生了概念漂移。

最近，胡阳等人［42］提出了一种基于 McDiarmid 边界的自适应加权概念漂移检测方法WMDDM。引入衰减函数对实例加权，赋予旧数据更低权值，提升新数据的影响力。该算法利用 McDiarmid 不等式得到加权分类正确率的置信边界，在检测到分类正确率下降超过置信边界时调节衰减因子，实现权值的动态改变。Yan［43］利用Hoeffding不等式提出了精准概念漂移检测方法（accurate concept drift detection method，ACDDM），该算法利用Hoeffding不等式来观察误差率的不一致性。假设Pt是当前的先验误差，Pmin是每个时间步长的最小误差，则时间t处最小误差和当前误差之间的差为ΔPt：

ΔPt=Pt-Pmin（4）

通过使用Hoeffding不等式确定漂移确认阈值drift，若ΔPt的平均值大于drift，则表明由于概念漂移，误差率出现不一致。实验表明ACDDM的漂移检测性能总体上优于其他算法。

2.1.2 基于被动自适应的方法

被动方法不主动检测概念漂移的出现，但是会通过不断地更新模型，如根据基分类器的性能动态地调整其权重，使得模型适应数据流中新的概念。被动方法中一般有根据分类器的准确率或其他性能指标进行动态加权以及保持集成的多样性水平等方法适应概念漂移。

1）基于性能反馈

Kolter等人［44］提出了动态加权多数算法（dynamic weighted majority，DWM），该算法根据分类器的错误率来更新权重。当集成性能严重下降时会训练新分类器用于更新集成。循环动态加权多数（recurring dynamic weighted majority，RDWM）［45］由主集合和次集合组成。主集合代表当前概念，并按照DWM算法进行训练和更新；而次集合由发生漂移时从主集合中复制的最准确的分类器组成。对于突变或渐变漂移，RDWM都具有良好的准确率。

准确度更新集成（accuracy updated ensemble，AUE）［46］算法通过使用在线组件分类器并根据当前分布进行更新来扩展AWE［47］，这种扩展使AUE在稳定性上优于AWE，同时对渐变漂移和突变漂移都能够很好地适应。在线准确度更新集成（online accuracy updated ensemble，OAUE）［48］是基于AUE的增量算法，它根据最近d个实例的误差来计算组件分类器的权重并创建一个新的分类器，以替换性能最弱的集成成员。Gu等人［49］提出了一种基于窗口自适应在线精度更新集成（window-adaptive online accuracy updated ensemble，WAOAUE）算法，并在集成中加入变化检测器来确定每个候选分类器的窗口大小，弥补了OAUE由于采用固定的窗口在适应突变漂移时存在的缺陷。

结合在线和基于块的集成的关键特征，可以有效地响应渐变漂移并快速响应突变漂移，上文所提AUE算法既是如此。知识最大化集成（knowledge-maximized ensemble，KME）［50］可以很好地解决具有有限标记实例的各种漂移场景，并且可以复用过去块中保存的标记实例，增强候选分类器的识别能力。Kappa更新集成（Kappa update ensemble，KUE）［51］使用Kappa统计来动态加权并选择基分类器。通过在特征的随机子集上训练基分类器，提供了更好的预测能力和对概念漂移的适应性。为了减少不合格分类器的影响，增加了弃权机制，该机制将选定的分类器从投票过程中删除。

2）多样性集成

为了保持对新旧概念的高度概括，保持高度多样化的集成是一个很好的策略。对于多样性没有单一的定义或衡量标准，在经典算法DDD［52］中使用Q统计量来定义多样性：

Qi，k=N11N00-N01N10N11N00+N01N10（5）

其中：Qi，k表示分类器Di和Dk之间的Q统计量；Nab表示Di分类结果为a，Dk分类结果为b的训练实例数量，1、0分别表示正确与错误分类。对于分类器集合，所有分类器对的平均Q统计量可以用作多样性的度量，较高/较低的平均值表示较低/较高的多样性。多样化动态加权多数（diversified dynamic weighted majority，DDWM）［53］維持了两组加权整体，它们在多样性水平上有所不同，并根据准确率对集成进行动态更新。实验表明，DDWM在Kappa统计、模型成本、评估时间和内存需求等方面均是高度资源有效的。

多样性也可以通过异构集成来实现。针对基分类器的类型异同，集成可分为同构与异构，bagging及boosting集成均为同构集成，而stacking算法属于异构集成。与同构集成不同，异构集成由不同的分类器模型组成，使得集成拥有较高的多样性。异构集成在批处理环境中已被证明是成功的，但不容易转移到数据流设置中，故Van Rijn等人［54］引入了一个在线性能评估框架，在整个流中该框架以不同的方式对集合成员的投票进行加权，并应用这种技术构建一个简单的新颖集成技术BLAST（best last的缩写）以快速进行异构集成。Museba等人［55］提出一种基于精度和多样性的异构动态集成选择方法（HDES-AD），该方法可以自动为特定概念选择最多样化和最准确的基本模型，以便在动态环境中长时间使用。异构动态加权多数（heterogeneous dynamic weighted majority，HDWM）［56］将DWM算法转变为异构集成，HDWM 会自动选择当前最佳的基本模型类型，通过智能切换基分类器来提高预测性能。ADES［57］提出了一种在线异构集成，它使用多样性和准确性作为评估指标来选择最佳集成，并创建不同多样性水平的集成，以最小的开销表现出了良好的性能。DDCW［58］利用动态加权方案和一种保持集成多样性的机制用于漂移数据流分类，该方法使用朴素贝叶斯（NB）以及霍夫丁树（Hoeffding tree）来构建其分类器集成，结果表明该模型在一定程度上优于其他同构集成。表1列出了本文所提及的异构在线集成算法所使用的基分类器，可以看出NB、Hoeffding tree等经典算法常被用作异构模型的基分类器。

2.2 不平衡数据流

不平衡数据流中最重要的特征就是倾斜的类分布。通常，少数类（正类）样本是更感兴趣的类别，但可能被忽略并被视为噪声。在在线学习场景中，这种困难会变得更加严重，因为无法看到数据的全貌，而且数据可能会动态变化。在线类不平衡问题的现有方法可大致分为算法級方法和数据级方法，前者通过在设计算法时考虑不同的误分类成本，从而使正实例的误分类代价高于负实例。在数据级方法的情况下，添加预处理步骤，通过对负类进行欠采样或对正类进行过采样，重新平衡类分布。

2.2.1 基于数据重采样的方法

基于数据重采样的方法主要有欠采样、过采样以及混合采样，欠采样通过减少多数类样本的实例，而过采样通过增加少数类样本的数量以实现类分布的平衡。

Wang等人［8］将重采样技术与在线bagging相结合，开发了两种基于重采样的在线学习算法，基于过采样的在线装袋（oversampling based online bagging，OOB）和基于欠采样的在线装袋（under-sampling based online bagging，UOB），通过使用时间衰减函数来动态捕捉失衡率，以解决数据流中的类不平衡问题。如果新实例属于少数类样本则OOB就会将泊松分布的参数λ调优为1/wk，wk代表当前类所占的比例，通过此方法间接地增加了少数类的训练次数。与OOB对应，当新实例属于多数类样本UOB则将参数设为（1-wk），从而实现多数类样本通过较小的k值进行相应的欠采样。之后，文献［59］又进一步改进了OOB和UOB内部的重采样策略，提出了使用自适应权重来维护OOB和UOB的方法，即WEOB1和WEOB2。WEOB1 使用OOB和UOB的归一化G-mean值作为它们的权重：

αo=gogo+gu，αu=gugo+gu（6）

其中：αo和αu分别表示OOB和UOB的权重；go和gu分别表示OOB和UOB的G-mean值。在WEOB2中，权重只能是二进制值（0或1），研究表明这两种加权集成方法的准确性均优于OOB，稳健性均优于UOB，而且WEOB2的G-mean值优于WEOB1。

诸如以上所述，许多研究都集中在不平衡二元分类问题上，对于多类不平衡问题，需要考虑更多的因素和设计更复杂的算法来处理增加的类别数量，因为多类问题增加了数据复杂性并加剧了不平衡分布。Wang等人［60］将研究扩展到多类场景，提出了基于多类过采样的在线装袋（MOOB）和基于多类欠采样的在线装袋（MUOB），该方法无须对多类问题进行类分解，并且允许集成学习器使用任何类型的基分类器。Olaitan等人［61］提出了一种基于窗口的方法（SCUT-DS），该算法应用在线K-均值聚类分析算法对多数类进行欠采样，并利用SMOTE算法通过窗口对少数类进行过采样。该算法的优点是不对类比率进行假设，但是该方法仅在有监督的学习环境中使用，因此有一定的局限性，在许多不平衡的在线学习应用程序中，标记所有实例是不可能的。Vafaie等人［62］提出了从具有缺失标签的多类不平衡流中学习的在线集成算法——基于SMOTE的改良在线集成（improved SMOTE online ensemble，ISOE）和改良的在线集成（improved online Snsemble，IOE）。在ISOE中使用SMOTE对最近窗口中的少数类实例进行过采样，同时根据召回率动态采样所有类，在IOE中根据性能和迄今为止看到的每个类的实例数量更改速率参数来重新平衡类的样本量。

利用分治策略将多类问题分解为单类子问题同样是一种可选的方法。Czarnowski［63］提出了使用过采样和实例选择技术（即欠采样）（WECOI），基于将单个多类分类问题分解为一组单类分类问题，使用分类器加权集成进行单类分类。该算法使用基于聚类的K均值算法合成实例，实现对少数类样本进行过采样，簇的中心用于表示参考实例，通过识别参考示例邻居之中的少数类，然后随机生成位于所识别的邻居之间的合成实例，如图6所示。经过验证所提消除数据流中类不平衡的方法有助于提高在线学习算法的性能。

2.2.2 基于代价敏感的方法

代价敏感算法考虑了不同的误分类成本。代价矩阵编码将样本从一类分类为另一类的惩罚（表2）。设C（i，j）表示将类i的实例预测为类j的成本，C（0，1）表示将正实例错误分类为负实例的成本。

代价敏感的集成学习方法通常通过在每次迭代bagging/boosting之前对数据进行有偏差的重新采样/重新加权来操纵误分类成本。Wang等人［64］提出了一个在线代价敏感集成学习框架，该框架将一批广泛使用的基于bagging和boosting的代价敏感学习算法推广到其在线版本：RUSBoost、SMOTEBoost、SMOTEBagging、AdaC2等。online bagging中的代价敏感是通过操纵泊松分布的参数实现的。在online UnderOverBagging中，新实例的重采样服从k-poisson（mC/M）（C>1），其中M为基分类器数量，m为基分类器编号。对于boosting算法则是通过制定权重更新规则来实现代价敏感。分析证实，由在线代价敏感集成学习算法生成的模型收敛于批量代价敏感集成的模型。Du等人［65］提出了EOBag算法，采用了多种均衡方法以减少不平衡数据流的影响。该算法通过式（7）计算误分类成本。

CDj=12×|N+|xj∈N+

12×|N-|xj∈N-（7）

其中：N+、N-分别表示正类与负类的实例数。从式（7）可以看出，正类的误分类成本CDj要明显大于负类。最后通过计算泛化误差进行加权投票得出最终结果。不使用准确率作为加权指标的原因是因为不同类样本的误分类成本不同，无法简单地通过使用基分类器的准确率来描述基分类器的权重。Loezer等人［66］提出的代价敏感自适应随机森林（cost-sensitive adaptive random forest，CSARF），是自适应随机森林（ARF）的变体并做了以下修改：使用马修斯相关系数（MCC）［67］为内部树分配权重，在与ARF和带重采样的随机森林（ARFRE）的对比中，表明基于误分类成本评估策略的使用是有效的。

本节从数据级和算法级两个方面介绍了在不平衡数据流中的在线集成分类算法。在数据级方法中，主要通过对数据进行重采样。在算法级方法，主要考虑的是不同类别的误分类成本。表3从算法所使用技术对本节所介绍的部分不平衡数据流分类算法进行了总结。

2.2.3 其他工作

在不平衡数据流方面同样也存在着概念漂移的问题，当与概念漂移相结合时，不平衡比率不再是静态的，它将随着流的进展而变化，例如少数类转变为多数类。因此，不仅要监视每个类的属性变化，还要监视其频率的变化。新类可能出现，旧类可能消失，这些现象对大多数现有算法构成了重大挑战。含概念漂移的不平衡数据分类也是目前研究的一个重点内容，用户兴趣推荐、社交媒体分析等现实案例都是很好的应用。

基于选择的重采样集成（selection-based resampling ensemble，SRE）［68］提出选择性重采样机制，该机制同时考虑概念漂移和数据困难因素，通过重用过去块的少数类数据来平衡当前类分布，然后通过评估每个保留的少数类样本与当前少数样本集之间的相似度来避免吸收漂移数据，最后采用加权投票进行预测。RE-DI集成模型［69］使用重采样缓冲区用于存储少数类的实例，以平衡数据随时间变化的不平衡分布，对于流中存在的概念漂移问题，RE-DI采用时间衰减策略以及增强机制进行处理，使模型更加关注数据流的新概念以及增加对少数类表现更好的基分类器权重。

此外，根据类分布中不平衡比率的动态变化进行动态采样与集成分类同样可以产生较好的效果。HIDC［70］通过估计类分布中的不平衡因子，对过采样和欠采样作出动态决策，有效处理类不平衡问题。并在集成性能下降时，将最差的集成成员替换为候选分类器，利用集成分类的加权机制快速响应各种类型的概念漂移，结果表明HIDC的性能始终优于对比算法DFGW-IS，并且随着实例的增加，F-score有着明显的提高。鲁棒在线自调整集成（robust online self-adjusting ensemble，ROSE）［71］则不关注当前的不平衡比率，而是通过在每个类上设置滑动窗口，以此来创建对类失衡不敏感的基分类器，实验证实ROSE是一种鲁棒且全面的集成模型，特别是在存在噪声和类不平衡漂移的情况下，能够同时保持竞争性的时间复杂度和内存消耗。基于窗口的DESW-ID算法［72］使用双重采样技术，首先使用泊松分布对数据流进行重新采样，如果当前数据处于高度不平衡状态，则使用存储少数类实例的窗口进行二次采样，以平衡数据分布。与UOB、OOB算法进行了对比实验，结果表明DESW-ID在F-score、G-mean以及召回率等五个指标中均具有很好的表现。

2.3 算法复杂度分析

算法复杂度是用来评价算法执行时间和资源消耗的度量，可以用来衡量一个算法的优劣，一般包括时间复杂度以及空间复杂度。通过研究算法的时空效率可以进一步了解算法的性能，从而尽可能地探索各种优化策略以提高算法效率。本节将对上文所涉及到的代表性算法进行时空效率的详细分析。

在概念漂移数据流算法中，DDM、RDDM以及BDDM等漂移检测方法主要由处理概念漂移的时间来决定，完整学习过程的算法复杂度还需要结合使用的底层分类算法。RDDM中有一个使用数组实现的圆形队列用于存储稳定概念的最小尺寸，故空间复杂度为O（min），而DDM无须存储，空间复杂度仅为O（1）。RDDM、DDM的时间复杂度分别为O（n×min）和O（n），其中n是处理实例的数量，因为RDDM在出现漂移时需要执行更多的迭代，而最小迭代只对n的小部分执行。对于BDDM算法，其使用了单窗口技术用于检测概念漂移，在大小为w的滑动窗口上计算，其时间复杂度为O（w），但在数据流的情况下其实例数n是未知的，故BDDM的时间复杂度是O（w×n）。而对于概念漂移自适应集成分类算法，算法复杂度主要取决于训练和加权过程。OAUE算法使用Hoeffding树作为其基分类器，由于Hoeffding树可以在常数时间内学习实例，训练k个树集合的时间复杂度为O（k），加权过程同样也仅需要恒定数量的操作，所以OAUE的时间复杂度为O（2k），其中k为用户定义的集成基分类器总数，即时间复杂度可近似为O（1）。OAUE的空间复杂度取决于所学习的概念，表示为O（kavcl+k（d+c）），其中a是属性的数量，v是每个属性的最大值数，c是类的数量，l是树中的叶子的数量。而k（d+c）为OAUE中的加权机制所需的时间，因为k、d和c均为常数，所以提出的加权方案与没有加权的模型相比，不会增加空间复杂度，即为O（kavcl）。KUE算法使用快速决策树（VFDT）作为基分类器，在每个块Si上更新k个VFDT树的时间复杂度为O（k|Si|），此外，KUE会在块Si上训练q个新树（q≤k），以准备替代最弱的集合成员，其时间复杂度为O（q|Si|），故KUE的时间复杂度为O（（k+q）|Si|）。VFDT的内存复杂度为O（rvlc），其中r为对总特征数f进行三维随机子空间投影后的特征数（r

对于不平衡数据流，算法复杂度主要取决于数据预处理所需要的时间及对再平衡数据分类的时间等。SRE算法的时间复杂度为O（N|M| log （|M|+a）+aN log a+3|M|N），其中N是数据块的数量，a是数据块大小，|M|是每个块包含的样例数。ROSE算法所使用的基分类器是VFDT，在第一个实例块S1集成初始化的时间复杂度为O（k），其中k为基分類器数量，集成模型在后续实例Si上的增量学习根据当前λ更新k个现有分类器的时间复杂度为O（kλ）。此外，在检测到概念漂移时，ROSE会训练另外k个分类器的背景集合，因此，ROSE的最坏情况下时间复杂度为O（2kλ|S|），其中|S|为数据块的数量。与KUE相同，VFDT的内存复杂度为O（fvlc），经过r维随机子空间投影后，有效地将VFDT的内存复杂度降低到O（rvlc）。ROSE还为每个类创建了一个大小为w的存储最新实例的滑动窗口，因此，由主集成中的k个分类器加上背景集成中的k个分类器组成的ROSE的最坏情况下空间复杂度为O（（2krvlc）+（|w|f）），其中f为特征数。

与单分类器相比，分类器集成在准确率、Kappa值等预测性能指标上有着显著的提升，但是时间和空间消耗都有所增加，这种情况是不可避免的，它是由集成结构所决定的。通过优化集成策略可以尽可能地提高时空效率，例如使用特征子空间对数据进行压缩、使用剪枝策略等。

3 算法性能对比与分析

本章对概念漂移数据流和不平衡数据流的部分在线集成分类方法进行了性能分析与对比，对使用的同一数据集进行了介绍并对比了所列算法的性能指标，并汇总了本文所介绍的算法使用的数据集、对比算法以及优缺点。

3.1 数据集介绍

本节对所使用的同一数据集进行了介绍，表4展示了使用相同数据集的算法。数据集描述如下。

a）LED：包含渐变漂移的数据集，由LED生成器生成用于预测七段二极管上显示的数据集，具有24个属性和 10个类别。每25 000个样本出现一次渐变漂移，共100 000个样本。

b）electricity：真实数据集，来自澳大利亚新南威尔士州电力市场能源价格的数据，用来测试检测器在真实数据中的效果，表中共有45 312个样本，每个样本具有7个属性和2个类。

c）random RBF：RBF生成器是一个使用随机质心创建新实例的合成数据集，每个质心由类标签、权重、位置和标准偏差定义。实例由50个属性和2个类描述，其中一个类是欠采样的，每1 000个实例产生一定的不平衡比率。

d）SEA：SEA生成器用于创建三个数据集，每个数据集包含10%的噪声。它包含三个取值从0～10的属性，第三个属性被视为噪声。并在每1 000个实例对其中一个类进行欠采样，以诱导类不平衡，少数类的基数占总数据的8%。

3.2 性能评估指标

本节介绍了部分评估数据流分类算法性能的指标，并结合2.2.2节的代价矩阵（混淆矩阵），给出了它们的计算方法，如表5所示。准确率（accuracy）、假阳性率（FPR）、假阴性率（FNR）、精度（precision）、召回率（recall） 等均为数据流分类算法中常用的性能评估指标。

3.3 算法性能对比

本节通过在使用相同数据集的条件下，对算法进行对比分析与总结，实验结论均由本文所提及的公开发表算法中的实验数据得出。表6从数据集、对比算法以及优缺点等方面对代表性算法进行总结。

3.3.1 概念漂移数据流

a）漂移检测方法。在数据大小为50 KB的LED突变漂移数据集上，相较于DDM与FHDDM，BDDM取得了50.24的最佳准确率，其余两者为49.14、47.66，并且在precision、recall、MCC指标上BDDM均表现出最优的性能，均为0.75。在与DDM、ADWIN、FHDDM的对比实验中，基分类器分别采用HT以及NB，MDDM算法的平均准确率最高为89.56。与基于窗口的算法FHDDM与MDDM相比，基于统计的算法SDDM具有最低的假阳性率和假阴性率，FPR及FNR均为0，而FHDDM与MDDM均为0.03与0.02。同样在electricity真实数据集上，BDDM、MDDM算法均取得了最佳的准确率，分别为85.68、83.47。在这两个数据集的实验数据中，基于统计的模型在平均准确率上比基于窗口的模型高约2.5%。

b）数据流分类方法。LED数据集中，在DDCW与DWM、KUE等算法的对比实验中，由KUE取得了最佳准确率0.893，仅使用HT作为其基分类器的异构算法DDCW具第二位0.873，DWM次之，为0.831。相较DDD算法，异构算法HEDS-AD在准确率以时间消耗方面均体现出明显的优势，DDD时空复杂度较高的原因是因为其维护了四个不同多样性的集成。在electricity数据集中，异构算法DDCW由于其较高的多样性，在准确率及F1-measure方面均优于对比算法，平均准确率与同构模型相比高约10%。

3.3.2 不平衡数据流

random RBF数据集中，在与OOB等算法的对比实验中，SRE在F-measure、G-mean、recall、AUC指标上均居于前列，其中F-measure、G-mean值取得了最佳，分别为62.22、84.35，准确率为92.52，仅次于OOB的93.05。相较于MUOB，ISOE和IOE在G-mean值上表现最好，分别为0.850和0.847，并无明显差别，这表明SMOTE在过采样少数类中的作用有限。而MUOB由于欠采样的数据量过多，导致表现不佳，G-mean值仅为0.741。当在数据流中加入了概念漂移之后，IOE的G-mean值没有明显的变化，而MUOB的G-mean从0.833降到了0.414。相较于OOB、UOB，DESW-ID算法在所有指标上均表现最佳，尤其是AUC达到了0.976 1，而OOB与UOB仅为0.760 9、0.638 8。SEA数据集中所有算法的平均表现不如RBF数据集，在ROSE与OOB、UOB的对比实验中，不论不平衡比率如何，ROSE算法在Kappa值及AUC值均取得了最高值，在不平衡比率为5的情况下，ROSE、OOB、UOB的AUC值分别为88.33、85.93、85.87。并且在静态及漂移不平衡比率的情况下ROSE的平均算法排名都在第二位左右。

4 下一步工作

目前针对复杂数据流的在線集成分类算法的研究已经有了很大的进展，但是仍然存在着许多挑战及有待解决的问题，需要进一步研究以优化算法来处理更加复杂的问题。下面将探讨目前所存在的挑战和问题，并给出下一步研究方向。

a）概念漂移数据流中动态选择集成的研究。概念漂移的存在对分类器的性能有很大的影响，一般处理方法包括主动检测漂移然后更新集成以及根据分类器的性能反馈自适应调整权重，但是在一些复杂概念漂移的情况下效果可能不太理想。未来可以考虑设计一种在线集成框架，包含一个静态分类器用于保存历史信息及多个动态分类器用于学习最新概念，根据分类器对最近实例的分类误差进行动态选择并加权决策。

b）不平衡数据流中的混合概念漂移问题研究。

对于不平衡数据流，概念漂移会变得更加难以处理，特别是在流中存在着多种漂移类型的情况下。在动态学习框架中，少数类实例没有得到充分的表示，在学习过程中容易被忽视，从而对于概念的变化非常的不敏感。在之后的研究中，可以考虑结合bagging集成和动态选择集成，并使用Kappa值与准确率的加权和组合基分类器的结果，处理类不平衡和多种概念漂移共存的问题。

c）噪声及其他复杂因素对在线学习的挑战。在线学习由于其过程的特殊性，一次学习一个实例，所以噪声对于在线算法的影响是极大的。且现实世界中的数据更加复杂，多标签、类重叠、多类不平衡等问题也对分类器的性能造成了极大的挑战。因此，在线集成分类算法如何应对噪声以及在更复杂的数据流中学习也是一个值得探讨的问题。

5 结束语

本文首次从概念漂移数据流以及不平衡数据流两个方面对复杂数据流在线集成分类算法进行了综述。首先，从集成策略的角度对算法进行了分类与总结，并对比了使用不同集成模型的在线集成分类算法的性能。其次，从主动和被动两方面对概念漂移、从算法级和数据级两方面对概念漂移数据流、不平衡数据流的在线集成分类方法做了详细的总结，并分析对比了代表性算法的时空复杂度以及在相同数据集下的实验结果，对算法所用的技术以及优缺点等进行了总结。最后，针对复杂数据流的在线集成分类算法所面临的挑战，提出了下一步研究方向以及復杂问题的解决思路。

参考文献：

［1］Sousa M R，Gama J，Brandao E.A new dynamic modeling framework for credit risk assessment［J］.Expert Systems with Applications，2016，45：341-351.

［2］Meseguer J，Puig V，Escobet T.Fault diagnosis using a timed discrete-event approach based on interval observers：application to sewer networks［J］.IEEE Trans on Systems，Man，and Cybernetics-Part A：Systems and Humans，2010，40（5）：900-916.

［3］Sun Yu，Tang Ke，Minku L L，et al.Online ensemble learning of data streams with gradually evolved classes［J］.IEEE Trans on Know-ledge and Data Engineering，2016，28（6）：1532-1545.

［4］Hoi S C H，Sahoo D，Lu Jing，et al.Online learning：a comprehensive survey［J］.Neurocomputing，2021，459：249-289.

［5］Dong Xibin，Yu Zhiwen，Cao Wenming，et al.A survey on ensemble learning［J］.Frontiers of Computer Science，2020，14：241-258.

［6］Oza N C，Russell S J.Online bagging and boosting［C］//Proc of the 8th International Workshop on Artificial Intelligence and Statistics.Piscataway，NJ：IEEE Press，2001：229-236.

［7］Santos S G T C，Gon?alves J P M，Silva G D S，et al.Speeding up recovery from concept drifts［C］//Proc of European Conference on Machine Learning and Principles and Practice of Knowledge Discovery in Databases.Piscataway，NJ：IEEE Press，2014：179-194.

［8］Wang Shuo，Minku L L，Yao Xin.A learning framework for online class imbalance learning［C］//Proc of IEEE Symposium on Computational Intelligence and Ensemble Learning.Piscataway，NJ：IEEE Press，2013：36-45.

［9］Gomes H M，Barddal J P，Enembreck F，et al.A survey on ensemble learning for data stream classification［J］.ACM Computing Surveys，2017，50（2）：1-36.

［10］杜诗语，韩萌，申明尧，等.概念漂移数据流集成分类算法综述［J］.计算机工程，2020，46（1）：15-24，30.（Du Shiyu，Han Meng，Shen Mingyao，et al.Survey of ensemble classification algorithms for data streams with concept drift［J］.Computer Engineering，2020，46（1）：15-24，30.

［11］张喜龙，韩萌，陈志强，等.面向复杂数据流的集成分类综述［J］.广西师范大学学报：自然科学版，2022，40（4）：1-21.（Zhang Xilong，Han Meng，Chen Zhiqiang，et al.Survey of ensemble classification methods for complex data stream［J］.Journal of Guangxi Normal University：Natural Science Edition，2022，40（4）：1-21.

［12］Mienye I D，Sun Yanxia.A survey of ensemble learning：concepts，algorithms，applications，and prospects［J］.IEEE Access，2022，10：99129-99149.

［13］翟婷婷，高阳，朱俊武.面向流数据分类的在线学习综述［J］.软件学报，2020，31（4）：912-931.（Zhai Tingting，Gao Yang，Zhu Junwu.Survey of online learning algorithms for streaming data classification［J］.Journal of Software，2020，31（4）：912-931.）

［14］Bifet A，Holmes G，Pfahringer B，et al.Improving adaptive bagging methods for evolving data streams［C］//Proc of the 1st Asian Confe-rence on Machine Learning.Berlin：Springer，2009：23-37.

［15］Bifet A，Holmes G，Pfahringer B.Leveraging bagging for evolving data streams［C］//Proc of European conference on Machine Learning and Knowledge Discovery in Databases.Berlin：Springer，2010：135-150.

［16］Bernardo A，Della V E.SMOTE-OB：combining SMOTE and online bagging for continuous rebalancing of evolving data streams［C］//Proc of IEEE International Conference on Big Data.Piscataway，NJ：IEEE Press，2021：5033-5042.

［17］Fernández A，Garcia S，Herrera F，et al.SMOTE for learning from imbalanced data：progress and challenges，marking the 15-year anniversary［J］.Journal of Artificial Intelligence Research，2018，61：863-905.

［18］Lughofer E.Evolving fuzzy systems—fundamentals，reliability，interpretability，useability，applications［M］//Handbook on Computational Intelligence.2016：67-135.

［19］Lughofer E，Pratama M，krjanc I.Online bagging of evolving fuzzy systems［J］.Information sciences，2021，570：16-33.

［20］Saffari A，Leistner C，Santner J，et al.On-line random forests［C］//Proc of the 3rd IEEE ICCV Workshop on On-line Computer Vision.Piscataway，NJ：IEEE Press，2009：1393-1400.

［21］王愛平，万国伟，程志全，等.支持在线学习的增量式极端随机森林分类器［J］.软件学报，2011，22（9）：2059-2074.（Wang Ai-ping，Wan Guowei，Cheng Zhiquan，et al.Incremental learning extremely random forest classifier for online learning［J］.Journal of Software，2011，22（9）：2059-2074.）

［22］Gomes H M，Bifet A，Read J，et al.Adaptive random forests for evolving data stream classification［J］.Machine Learning，2017，106：1469-1495.

［23］De Barros R S M，De Carvalho S S G T，Júnior P M G.A boosting-like online learning ensemble［C］//Proc of International Joint Conference on Neural Networks.Piscataway，NJ：IEEE Press，2016：1871-1878.

［24］Santos S G T C，De Barros R S M.Online AdaBoost-based methods for multiclass problems［J］.Artificial Intelligence Review，2020，53：1293-1322.

［25］Baidari I，Honnikoll N.Accuracy weighted diversity-based online boosting［J］.Expert Systems with Applications，2020，160：113723.

［26］Honnikoll N，Baidari I.Mean error rate weighted online boosting me-thod［J］.The Computer Journal，2023，66（1）：1-15.

［27］Matthews B W.Comparison of the predicted and observed secondary structure of T4 phage lysozyme［J］.Biochimica et Biophysica Acta（BBA）-Protein Structure，1975，405（2）：442-451.

［28］Frías-Blanco I，Verdecia-Cabrera A，Ortiz-Díaz A，et al.Fast adaptive stacking of ensembles［C］//Proc of the 31st Annual ACM Symposium on Applied Computing.New York：ACM Press，2016：929-934.

［29］Ortiz-Díaz A A，Baldo F，Marino L M P，et al.Fase-AL-adaptation of fast adaptive stacking of ensembles for supporting active learning［EB/OL］.（2020）.https：//arxiv.org/abs/2001.11466.

［30］Jiang Weili，Chen Zhenhua，Xiang Yan，et al.SSEM：a novel self-adaptive stacking ensemble model for classification［J］.IEEE Access，2019，7：120337-120349.

［31］Büyük?akir A，Bonab H，Can F.A novel online stacked ensemble for multi-label stream classification［C］//Proc of the 27th ACM International Conference on Information and Knowledge Management.New York：ACM Press，2018：1063-1072.

［32］Guo Husheng，Zhang Shuai，Wang Wenjian.Selective ensemble-based online adaptive deep neural networks for streaming data with concept drift［J］.Neural Networks，2021，142：437-456.

［33］Gama J，Medas P，Castillo G，et al.Learning with drift detection［C］//Proc of the 17th Advances in Artificial Intelligence.Berlin：Springer，2004：286-295.

［34］Baena-García M，Del Campo-vila J，Fidalgo R，et al.Early drift detection method［C］//Proc of the 4th International Workshop on Knowledge Discovery from Data Streams.2006：77-86.

［35］Barros R S M，Cabral D R L，Gon?alves Jr P M，et al.RDDM：reactive drift detection method［J］.Expert Systems with Applications，2017，90：344-355.

［36］Baidari I，Honnikoll N.Bhattacharyya distance based concept drift detection method for evolving data stream［J］.Expert Systems with Applications，2021，183：115303.

［37］Micevska S，Awad A，Sakr S.SDDM：an interpretable statistical concept drift detection method for data streams［J］.Journal of Intelligent Information Systems，2021，56：459-484.

［38］Bifet A，Gavalda R.Learning from time-changing data with adaptive windowing［C］//Proc of SIAM International Conference on Data Mi-ning.［S.l.］：Society for Industrial and Applied Mathematics，2007：443-448.

［39］Frias-Blanco I，Del Campo-vila J，Ramos-Jimenez G，et al.Online and non-parametric drift detection methods based on Hoeffdings bounds［J］.IEEE Trans on Knowledge and Data Engineering，2014，27（3）：810-823.

［40］Pesaranghader A，Viktor H L.Fast Hoeffding drift detection method for evolving data streams［C］//Proc of Machine Learning and Knowledge Discovery in Databases.Cham：Springer，2016：96-111.

［41］Pesaranghader A，Viktor H L，Paquet E.McDiarmid drift detection methods for evolving data streams［C］//Proc of International Joint Conference on Neural Networks.Piscataway，NJ：IEEE Press，2018：1-9.

［42］胡陽，孙自强.基于 McDiarmid 边界的自适应加权概念漂移检测方法［J］.华东理工大学学报：自然科学版，2023，49（2）：1-10.（Hu Yang，Sun Ziqiang.Weight adaptive concept drift detection me-thod based on McDiarmid boundary［J］.Journal of East China University of Science and Technology，2023，49（3）：1-10.）

［43］Yan M M W.Accurate detecting concept drift in evolving data streams［J］.ICT Express，2020，6（4）：332-338.

［44］Kolter J Z，Maloof M A.Dynamic weighted majority：an ensemble method for drifting concepts［J］.The Journal of Machine Learning Research，2007，8：2755-2790.

［45］Sidhu P，Bhatia M P S.A two ensemble system to handle concept drifting data streams：recurring dynamic weighted majority［J］.International Journal of Machine Learning and Cybernetics，2019，10：563-578.

［46］Brzeziński D，Stefanowski J.Accuracy updated ensemble for data streams with concept drift［C］//Proc of the 6th International Confe-rence on Hybrid Artificial Intelligence Systems.Berlin：Springer，2011：155-163.

［47］Wang Haixun，Fan Wei，Yu P S，et al.Mining concept-drifting data streams using ensemble classifiers［C］//Proc of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York：ACM Press，2003：226-235.

［48］Brzezinski D，Stefanowski J.Combining block-based and online me-thods in learning ensembles from concept drifting data streams［J］.Information Sciences，2014，265：50-67.

［49］Gu Xiaofeng，Xu Jiawen，Huang Shijing，et al.An improving online accuracy updated ensemble method in learning from evolving data streams［C］//Proc of the 11th International Computer Conference on Wavelet Active Media Technology and Information Processing.Pisca-taway，NJ：IEEE Press，2014：430-433.

［50］Ren Siqi，Liao Bo，Zhu Wen，et al.Knowledge-maximized ensemble algorithm for different types of concept drift［J］.Information Sciences，2018，430：261-281.

［51］Cano A，Krawczyk B.Kappa updated ensemble for drifting data stream mining［J］.Machine Learning，2020，109：175-218.

［52］Minku L L，Yao Xin.DDD：a new ensemble approach for dealing with concept drift［J］.IEEE Trans on Knowledge and Data Enginee-ring，2011，24（4）：619-633.

［53］Sidhu P，Bhatia M P S.A novel online ensemble approach to handle concept drifting data streams：diversified dynamic weighted majority［J］.International Journal of Machine Learning and Cyberne-tics，2018，9：37-61.

［54］Van Rijn J N，Holmes G，Pfahringer B，et al.Having a blast：meta-learning and heterogeneous ensembles for data streams［C］//Proc of IEEE International Conference on Data Mining.Piscataway，NJ：IEEE Press，2015：1003-1008.

［55］Museba T，Nelwamondo F，Ouahada K.An adaptive heterogeneous online learning ensemble classifier for nonstationary environments［J］.Computational Intelligence and Neuroscience，2021，2021：article ID 6669706.

［56］Idrees M M，Minku L L，Stahl F，et al.A heterogeneous online lear-ning ensemble for non-stationary environments［J］.Knowledge-Based Systems，2020，188：104983.

［57］Museba T，Nelwamondo F，Ouahada K.ADES：a new ensemble diversity-based approach for handling concept drift［J］.Mobile Information Systems，2021，2021：1-17.

［58］Sarnovsky M，Kolarik M.Classification of the drifting data streams using heterogeneous diversified dynamic class-weighted ensemble［J］.PeerJ Computer Science，2021，7：e459.

［59］Wang Shuo，Minku L L，Yao Xin.Resampling-based ensemble me-thods for online class imbalance learning［J］.IEEE Trans on Know-ledge and Data Engineering，2014，27（5）：1356-1368.

［60］Wang Shuo，Minku L L，Yao Xin.Dealing with multiple classes in online class imbalance learning［C］//Proc of the 25th International Joint Conference on Artificial Intelligence.Palo Alto，CA：AAAI Press，2016：2118-2124.

［61］Olaitan O M，Viktor H L.SCUT-DS：learning from multi-class imba-lanced Canadian weather data［C］//Proc of the 24th International Symposium on Foundations of Intelligent Systems.Cham：Springer，2018：291-301.

［62］Vafaie P，Viktor H，Michalowski W.Multi-class imbalanced semi-supervised learning from streams through online ensembles［C］//Proc of International Conference on Data Mining Workshops.Washington DC：IEEE Computer Society，2020：867-874.

［63］Czarnowski I.Weighted ensemble with one-class classification and over-sampling and instance selection（WECOI）：an approach for lear-ning from imbalanced data streams［J］.Journal of Computational Science，2022，61：101614.

［64］Wang Boyu，Pineau J.Online bagging and boosting for imbalanced data streams［J］.IEEE Trans on Knowledge and Data Engineering，2016，28（12）：3353-3366.

［65］Du Hongle，Zhang Yan，Gang Ke，et al.Online ensemble learning algorithm for imbalanced data stream［J］.Applied Soft Computing，2021，107：107378.

［66］Loezer L，Enembreck F，Barddal J P，et al.Cost-sensitive learning for imbalanced data streams［C］//Proc of the 35th Annual ACM Symposium on Applied Computing.New York：ACM Press，2020：498-504.

［67］Zhu Qiuming.On the performance of Matthews correlation coefficient（MCC） for imbalanced dataset［J］.Pattern Recognition Letters，2020，136：71-80.

［68］Ren Siqi，Zhu Wen，Liao Bo，et al.Selection-based resampling ensemble algorithm for nonstationary imbalanced stream data learning［J］.Knowledge-Based Systems，2019，163：705-722.

［69］Zhang Hang，Liu Weike，Wang Shuo，et al.Resample-based ensemble framework for drifting imbalanced data streams［J］.IEEE Access，2019，7：65103-65115.

［70］Ancy S，Paulraj D.Handling imbalanced data with concept drift by applying dynamic sampling and ensemble classification model［J］.Computer Communications，2020，153：553-560.

［71］Cano A，Krawczyk B.ROSE：robust online self-adjusting ensemble for continual learning on imbalanced drifting data streams［J］.Machine Learning，2022，111（7）：2561-2599.

［72］Han Men，Zhang Xilong，Chen Zhiqiang，et al.Dynamic ensemble selection classification algorithm based on window over imbalanced drift data stream［J］.Knowledge and Information Systems，2023，65（3）：1105-1128.