线性正则正余弦加权卷积及其应用

王小霞,冯 强

(延安大学 数学与计算机科学学院,陕西 延安 716099)

线性正则变换(linear canonical transform,LCT)[1-5]被广泛应用于应用数学、光学和信号处理等领域,是傅里叶变换(fourier transform,FT)[6-7]、分数阶傅里叶变换(fractional fourier transform,FRFT)[8-9]的广义形式。在线性正则变换的基础上定义的线性正则正弦变换(linear canonical sine transform,LCST)[10]与线性正则余弦变换(linear canonical cosine transform,LCCT)[10]是傅里叶正弦变换(fourier sine transform,FST)[11-12]与傅里叶余弦变换(fourier cosine transform,FCT)[11-12]的广义形式。由于LCST与LCCT的计算复杂度是线性正则变换计算复杂度的一半,在处理奇偶信号问题上具有独特的优势,因此,在应用数学、光学系统和信号处理领域研究线性正则正余弦变换卷积运算以及卷积定理非常重要。

近年来,许多学者对傅里叶正余弦变换卷积运算[11-12]、分数阶傅里叶正余弦变换卷积运算[13-15]、线性正则正余弦变换卷积运算[10]进行了深入研究,例如,THAO等[12]研究了傅里叶正余弦加权广义卷积,并给出了它在求解积分方程组中的应用,冯强[13-16]等研究了分数阶傅里叶正余弦变换卷积定理,讨论了卷积类积分方程的求解问题,文献[10]给出了线性正则正余弦变换卷积运算及其相应的卷积定理,并设计了一类基于卷积定理的线性正则正余弦变换域带限信号的乘性滤波模型。

线性正则正余弦变换相对于傅里叶正余弦变换及分数阶傅里叶正余弦变换更具有灵活性,因此,研究线性正则正余弦变换卷积运算及其卷积定理非常有意义。本文在现有基础上,首先,定义了LCST-LCCT、LCCT-LCST卷积运算及其加权卷积运算并深入挖掘了与其相关的卷积定理;其次,给出了所得卷积与已有的FCT、FST-FCT、FCT-FST、LCCT、LCST卷积运算的关系;最后,讨论了两类卷积类积分方程组的解,并给出了该类方程解的一般形式。

1 预备知识

定义1[17-18]设函数f(t)∈L1(R),A=(a,b,c,d)为参数矩阵,其中,ad-bc=1,则LCT定义为

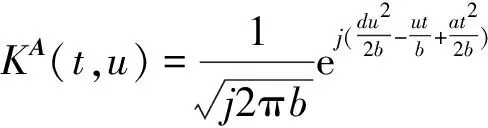
f(t)的线性正则变换的逆变换可以表示为

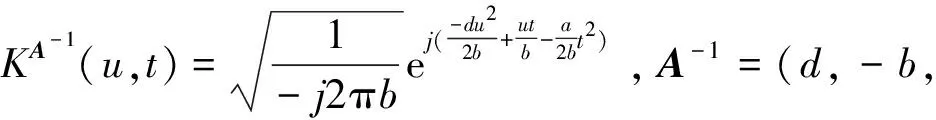
当A=(0,1,-1,0)时,LCT就变为FT[6-7]。

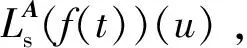
(1)

其逆变换为

(2)

其逆变换为

当A=(0,1,-1,0)时,上述LCST和LCCT就退化为经典的FST和FCT[20]:

与

引理1[21]设f(t),g(t)∈L1(R),满足如下FCT卷积运算:

g(t+τ))dτ

(3)

则有如下卷积定理,

引理2[22]设f(t),g(t)∈L1(R),满足如下FST-FCT卷积运算:

g(t+τ))dτ

(4)

则有如下卷积定理,

引理3[22]设f(t),g(t)∈L1(R),满足如下FCT-FST卷积运算:

sgn(t-τ)g(|t-τ|))dτ

(5)

则有如下卷积定理,

引理4[10]设f(t),g(t)∈L1(R),满足如下LCST加权卷积运算:

(6)

则有如下卷积定理,

引理5[10]设f(t),g(t)∈L1(R),满足如下LCCT卷积运算:

(7)

则有如下卷积定理,

2 主要结果

2.1 LCST与LCCT加权卷积运算

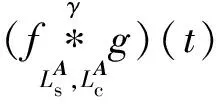
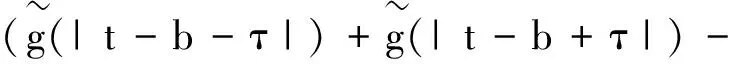
(8)

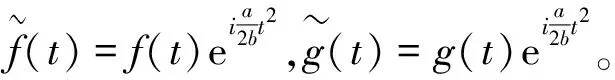
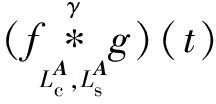
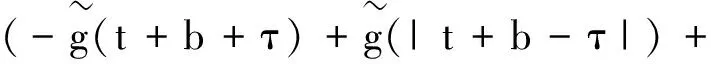
(9)

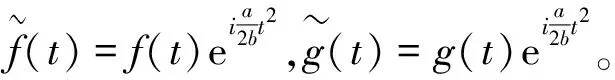
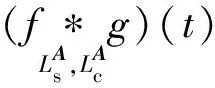
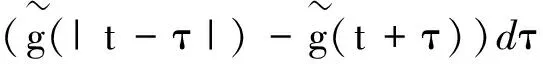
(10)

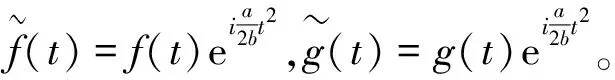
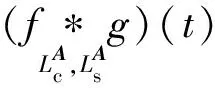
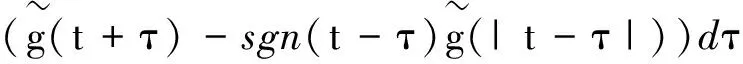
(11)

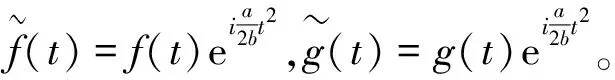
2.2 LCST与LCCT加权卷积定理

本节在LCST卷积运算与LCCT卷积运算及其加权卷积运算的基础上,推导出相应的卷积定理。

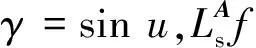
(12)

其中,u>0。

因为

同理可得

从而

其次,证明式(12)。根据式(1)式(2)及定义4,有

(13)

由于

(14)

由式(13)式(14)可得

f(p)g(|b+p-q|)dpdq

(15)

同理可得

文化自信关系到一个国家综合国力和国际地位的提升。中国特色社会主义进入新时代，中国社会和经济的发展为当代中国文化自信奠定了坚实的物质基础，但我国社会主要矛盾的转化又使文化建设面对许多新的问题和挑战。

(16)

由式(15)式(16)以及定义4,可得

则

因此,定理得证。

(17)

其中,u>0。

证明定理2的证明类似于定理1。

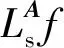
(18)

证明定理3的证明类似于定理1。

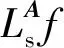
(19)

其中,u>0。

证明定理4的证明类似于定理1。

2.3 LCST与LCCT加权卷积运算与已有卷积运算之间的关系

本节将继续研究LCST卷积运算与LCCT卷积运算及其加权卷积运算与FST卷积运算和FCT卷积运算之间的关系。

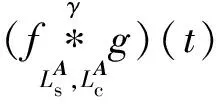
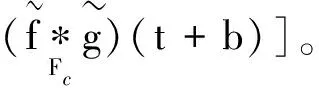
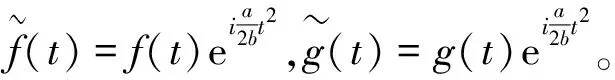
证明由定义4可得

由式(3)可得

因此,定理得证。

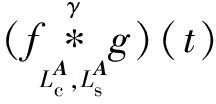
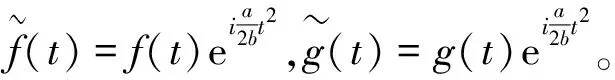
证明定理6的证明类似于定理5。

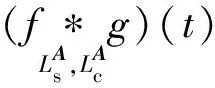
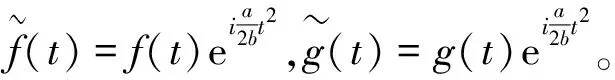
证明定理7的证明类似于定理5。

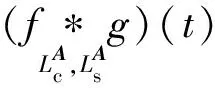
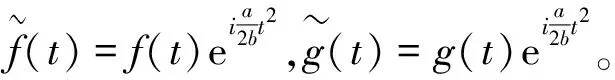
证明定理8的证明类似于定理5。

3 线性正则正余弦卷积运算在积分方程中的应用

积分方程在很多应用中都很重要,涉及辐射能量传递,膜或轴的振荡问题。因此,研究卷积类积分方程组的解是一个热点。

下面讨论两类卷积类积分方程组的解。

3.1 第一类积分方程

(20)

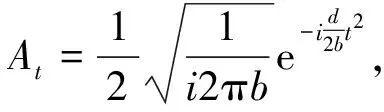
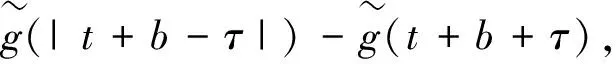
定理9假设条件Δ=1-Λ≠0成立,其中,

则式(20)存在唯一解

其中,ψ∈R+且满足

(21)

证明卷积类积分方程组(20)可改写为

(22)

对上式两边分别做LCST与LCCT,则可得

由于

利用Wiener-Levis定理[23]以及式(21)可得

从而可得

同理可得

利用Wiener-Levis定理[23]以及式(12)可得

则可得

因此,定理得证。

3.2 第二类积分方程

(23)

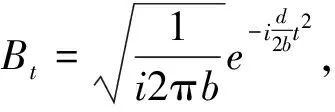
定理10假设条件Δ=1-Λ≠0成立,其中,

则式(14)存在唯一解

其中,ψ∈R+且满足

(24)

证明式(23)卷积类积分方程组可改写

(25)

对式(25)两边分别做LCST与LCCT,则方程组改写为

由于

利用Wiener-Levis定理[23]以及式(24)可得

从而可得

同理可得

利用Wiener-Levis定理[23]以及式(24)可得

则可得

因此,定理得证。

4 结论

卷积类积分方程组在应用数学、工程力学中具有广泛的应用。本文定义了LCST-LCCT、LCCT-LCST卷积运算及其加权卷积运算,研究了线性正则正余弦卷积运算与已有卷积运算之间的关系,推导出相应的卷积定理,所得结果是经典傅里叶正余弦卷积理论在线性正则域内的进一步拓展,丰富了线性正则变换域卷积理论,并利用所得结果给出两类卷积类积分方程组解的一般形式。