基于Zernike矩和拼贴误差的布料图案检索算法

张 琴,曹一青

(莆田学院 机电与信息工程学院,福建 莆田 351100)

纺织品行业中,布料图案的检索和分类依靠人工经验完成,效率较低、成本较高且准确率不高,无法满足高效准确地检索出特定布料图案的需求,因此,本文拟实现一种检索效果和效率兼具的布料花案图像检索算法。布料图案的花纹相对繁杂,且图案拍摄过程不当可能会引起图像的角度随意和非平面结构等问题,这些问题给图像检索带来了一定的困难。单一图像特征用于检索无法准确地描述布料图案的全部信息,导致检索准确率不高。DING等[1]利用尺度不变特征变换(scale-invariant feature transform,SIFT)和高斯函数获取了畲族服装图像中的特征,并依据获得的特征对图像进行了分类,该方法可有效识别不同类别的畲族服装。WANG等[2]利用深度卷积神经网络对跨域图像进行分类显示,该方法可获得较好的跨域图像检索效果。JING等[3]提出了一种将颜色矩和Gist特征描述的布料图案相融合的检索方法,该算法的平均查准率为86.3%,平均查全率为53.3%。ZHANG等[4]提出了一种基于低层纹理特征的羊毛布料图案检索算法,平均检索准确率在85%以上,平均检索时间为1.4 s。IHSAN等[5]提出了一种基于完全神经网络、超像素特征提取网络结构(superpixels features extractor network,SP-FEN)和简单线性迭代聚类算法(simple linear iterative clustering,SLIC)的时装图像的超像素特征,研究显示该方法可对时装图像进行较好的像素分割和服装解析,但获取数据集的成本较高。CHEN等[6]针对跨域服装图像检索提出了一种深度学习的检索方法,准确率为78.1%。

由于Zernike矩具有旋转、尺度和平移不变性,且能清晰地描述图像轮廓细节的特征,目前被广泛应用于布料图案的特征提取[7]。但是,Zernike矩在应用中存在计算量大和阶数越高对噪声越敏感等问题[8-9];因此,在实际应用中往往应用Zernike低阶矩来作为检索特征。分形域的拼贴误差是一种分形编码参数,利用其解码图像可获得高质量的压缩图像,且计算复杂度低[10]。为进一步提高布料图案检索的平均查全率、查准率和检索效率,本文提出了一种将低阶Zernike矩和分形域拼贴误差相结合的布料图案检索算法(zernike moment and collage error,ZMCE),并通过实验验证了该算法的有效性。

1 算法设计

1.1 图像f(x,y)的Zernike矩的计算

图像f(x,y)的Zernike矩是一组极坐标下的单位圆内的正交多项式Vnm(x,y)[11],其可表示为

Vnm(x,y) =Vnm(ρ,θ) =Rnmejmθ

(1)

式(1)中,Rnm为实值多项式,其表达式为

(2)

n阶m次Zernike矩的表达式[9]为

(3)

θ=arctan(y/x)(x>-1,y<1)

(4)

假设图像旋转α角度后,θ′=θ-α,则旋转后的Zernike矩可表示为

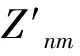
(5)

(6)

布料图案的Zernike矩的计算步骤为:

(1)对布料图案中的目标区域与背景进行分割,然后利用零阶几何矩计算目标的面积,零阶几何矩的计算公式为

m00= ∬f(x,y)dxdy

(7)

(2)根据式(6)计算数字图像f(x,y)在单位圆内的Zernike矩。

(3)利用式|Znm|′=|Znm|/m00[11]对Zernike矩进行归一化处理,并将模值|Znm|′作为布料图案检索的特征量。

(4)分别计算图像的前8阶低阶矩,即|Z00|′,|Z20|′,|Z33|′,|Z42|′,|Z53|′,|Z64|′,|Z71|′,|Z80|′和9、10、11阶高阶矩|Z91|′,|Z10.0|′,|Z11.1|′。将高阶和低阶Zernike矩分别作为布料图案检索的特征量。

1.2 分形域拼贴误差的计算

实验图像来源于某服装设计企业的面料库,共选取800张(尺寸大小为512×512)。将每副图像按顺时针旋转30°后共计获得1 600张实验图像。图1为面料库中部分布料图案。

图1 面料库中的部分布料图案Fig.1 Part of the fabric images

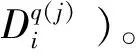
(8)

(9)

式中,U块的灰度值均为1。由式(9)可知,此时虽然值域块与定义域块已经达到最佳匹配,但仍存在如下偏差。

(10)

于是根据式(10)中的E(R,D)可将拼贴误差[15]定义为

(11)

由文献[13]可知,当式(9)中的si和oi分别为

(12)

(13)

时,式(9)有最小值。

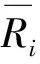
本文以图1中的Plaid(a)和(b),Stripes(a)和(c),Patterned(a)、(b)、(c)和Plant(a)为例对拼贴误差表征图像纹理和边缘信息的能力进行说明。首先,对图像进行灰度化预处理;其次,将图像分别分割成大小为4×4的Ri块和8×8的Di块;最后,利用式(9)—(13)计算出图像的拼贴误差,并将拼贴误差由小到大分为Ⅰ、Ⅱ、Ⅲ3类。其中,Ⅰ类用白色表示,Ⅱ类用灰色表示,Ⅲ类用黑色表示。

图2为布料图案与拼贴误差输出图像的对比图。由图2可知,拼贴误差可消除图像信息冗余和保留原图像的纹理和边缘信息,可应用于布料图案的检索。

注:(a)和(c)为灰度图;(b)和(d)为拼贴误差输出图像。

2 布料图案的相似度匹配算法

Zernike矩和分形域拼贴误差相结合的布料图案检索算法的实现流程如图3所示。该算法采用欧式距离(Euclidean距离)对比两幅布料图像的相似度。欧式距离的计算公式为

(14)

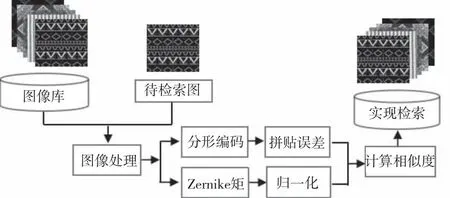
图3 本文算法(ZMCE)的示意框图Fig.3 The schematic block diagram of the proposed algorithm (ZMCE)

设待检索布料图像为Q,图像库中某一布料图像为R,则基于Zernike矩的相似度计算公式为

(15)

式中:Zi(Q)和Zi(R)分别表示两幅图像的Zernike矩;dZ(Q,R)为两幅图像Zernike矩的差异。基于分形域拼贴误差的相似度计算公式为

(16)

式中:E(Q)和E(R)分别表示两幅图像的拼贴误差;dE(Q,R)为两幅图像拼贴误差的差异。由此可得两幅图像之间的总相似度距离的计算公式为

d=λ1dZ(Q,R)+λ2dE(Q,R)

(17)

式中:λ1(0<λ1<1)和λ2(0<λ2<1)为两种特征量测度的权重,其值是经过多次不同实验对象进行图像检索实验结果得出的,且λ1+λ2=1。

本文利用查全率(R)、查准率(P)[16]和二者的加权调和平均(F值)[17]来获取最佳特征量测度的权重。查全率、查准率和F值的计算公式为:

(18)

(19)

(20)

式中:r和N分别表示检索出的相似和不相似图像的个数;r+N表示检索返回的图像总数;M表示未被检索出的相似图像个数;r+M表示相似图像的总数。

为了考察不同阶Zernike矩检索效果,本文分别采用前8阶矩和9、10、11阶高阶矩作为布料图案检索的特征量,分别计算了低阶和高阶矩下的平均查全率和平均查准率和F值,结果见表1和图4。均采用9组不同的λ1值和λ2值,实验图像为未旋转前的800幅图像。由表1可以看出,当前8阶矩和拼贴误差两种特征量测度的权重λ1和λ2均为0.5时,其F值均最大,查全率和F值较高,且对噪声不敏感。

表1 不同权重下平均查准率和平均查全率的加权调和平均Tab.1 Weighted harmonic average of average precision and average recall under different weights

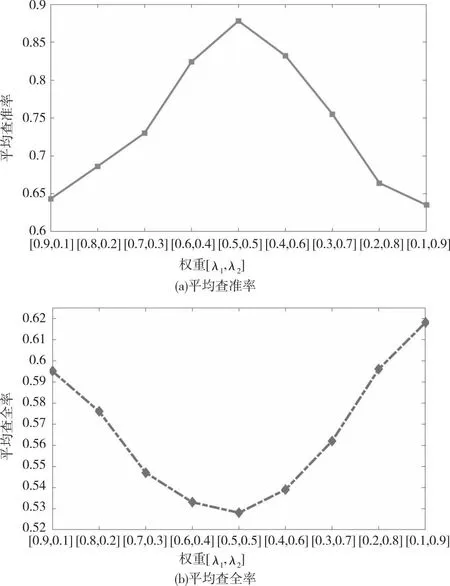
图4 不同权重值下的图像检索效果Fig.4 Image retrieval effect under different weights

再采用9、10和11阶高阶Zernike矩进行同样实验。结果表明,权重取λ1=0.5,λ2=0.5时,F值最大,如表2所示。

表2 高阶Zernike矩下的实验结果Tab.2 Experimental results under higher order Zernike moments

由表2可知,高阶Zernike矩下的平均查准率为0.883,高于低阶矩下的0.878,但查全率略低,加权调和平均为0.654 5,略低于低阶矩下的0.659 4。因为低阶矩能够有效反映图像的轮廓信息,高阶矩则更多体现细节信息,分形域的拼贴误差可表征图像纹理,且高阶矩对噪声较敏感,因此,本文采用前8阶低阶矩作为图像检索特征。

3 实验结果与分析

为验证本文方法的有效性,将本文ZMCE算法与基本分形算法(basic fractal coding, BFC)[18]、单一拼贴误差算法(single collage error algorithm, SCE)[19]、联合正交化分形参数和改进Hu不变矩算法(orthogonalization fractal parameters and improved Hu moment invariant algorithm, OFH)[20]以及文献[4]中基于主色调(dominant colors,DCs)和颜色矩(color moments,CMs)特征的算法作了对比分析。实验采用MATLAB R2018a软件,计算机配置为:Intel Core i5处理器,8 GB内存,64位Windows 10操作系统。实验图像为服装设计企业面料库中的800张布料图案图像和这些图像旋转后的800张图像,共计1 600张,大小为512×512。

为了保证实验对比数据的有效性,以上算法均在相同的图像上进行,且均采用Euclidean距离作为相似度计算公式。实验时,以布料图案库为检索库,并将每一张布料图案依次作为各算法待检索图像(共计860张)。根据公式(18)—(20),计算出图1中所列出的4类图案的查准率和查全率,如图5和图6所示。

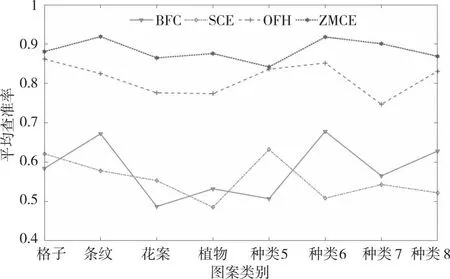
图5 不同算法下8类图案的平均查准率Fig.5 The average precision of 8 kinds of images under different algorithms

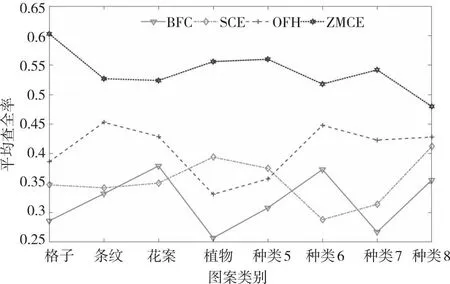
图6 不同算法下8类图案的平均查全率Fig.6 The average recall of 8 kinds of images under different algorithms

由图5图6分析可知,本文算法(ZMCE)的平均查准率(0.919)和查全率(0.603)显著高于BFC算法、SCE算法和OFH算法。

为了进一步验证本文算法的有效性,将本文算法与SCE、BFC、OFH算法和文献[4]中的算法进行了检索对比(实验图像为图像库中的1 600张布料图像),结果如表3所示。由表3可知,本文算法的平均查准率和查全率比BFC算法、SCE算法、OFH算法和文献[4]的算法分别高出0.379、0.352、0.08、0.014,0.202、0.184、0.122、0.091;检索速度也显著快于SCE算法、BFC算法和OFH算法(与文献[4]算法速度几乎相同)。

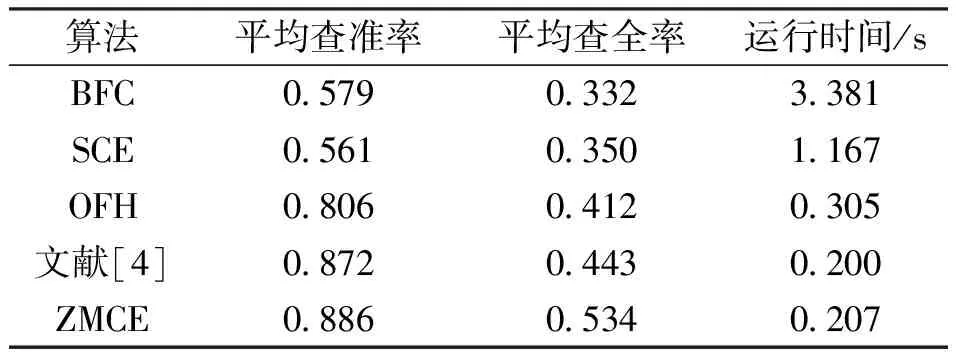
表3 不同算法对图像的检索效率Tab.3 The retrieval efficiency of different algorithms

本文算法优于其他4种算法的原因是:本文算法不仅采用了具有图像旋转不变性、尺度和平移不变性、低噪声敏感度等优势的Zernike矩,而且还采用了分形域的拼贴误差作为检索特征量;BFC算法仅采用了分形参数作为图像检索特征量,且定义域块与值域块的匹配过程较为复杂;OFH算法的检索效果虽相对较好,但检索特征量的Hu不变矩的鲁棒性较弱;SCE算法仅采用了拼贴误差作为检索特征量;文献[4]中的算法采用的是基于主色(DC)和色矩(CM)的检索方法,该方法的鲁棒性有待提高。

4 结论

本文针对布料图案检索过程中存在的准确率不高,效率低等问题,提出将Zernike矩和分形域拼贴误差联合用于布料图案检索。该算法中,适用于具有一定自相似性图像的拼贴误差,能够表征图像细节信息、计算复杂度低且压缩比较高。与此同时,Zernike矩具有旋转不变性、尺度和平移不变性、低噪声敏感等特点。研究表明,本文提出的ZMCE算法对布料图案检索的综合效率显著优于SCE算、BFC算法、OFH算法和文献[4]中的算法,因此,该算法可为纺织品企业的布料图案检索提供良好参考。在今后的研究中,我们将继续探讨如何更有效地提取布料图案的特征量,以进一步提高本文方法的检索效果。