随机多路径车辆路径问题及其算法

徐 鹏,卢翰林

(河海大学 土木与交通学院,江苏 南京 210098)

近年来,以小批量、多频次、多品种、时效性强为主要特征的城市配送业务增长迅猛。以快递业为例,根据国家邮政局统计,我国快递业务量从2012年的56.85亿件增长到2022年的1 105.8亿件[1],十年间增长了近20倍。面对早已拥堵不堪的城市道路,规模庞大的城市配送业务让“最后一公里”[2]难题变得更加严峻。因此,为城市配送业务提供核心解决方案的车辆路径问题(vehicle routing problem,VRP),受到物流研究人员和从业人员的关注[3]。针对不同的应用场景,国内外学者对经典的VRP进行了各种各样的拓展[4-6],取得了丰硕的研究成果。王勇等[7]通过引入客户信用度的测度方法,建立了考虑客户信用度的VRP模型,并设计了一种遗传-禁忌搜索混合算法,不仅可以优化配送路线,降低成本,还能保证客户的满意度;张冬青等[8]针对配送车辆在真实路网中行驶时间的随机性,建立了考虑时空相关随机行驶时间的VRP模型,并设计了一种结合可变邻域下降算法的混合粒子群算法,解决了时空相关下的车辆路径规划问题;Agussurja等[9]针对客户需求的随机性,建立了多周期的随机VRP模型,并利用随机动态规划方法进行了求解,解决随机多期末端骑行共享问题;柳伍生等[10]从城市配送的发展趋势出发,建立了 “无人机-车辆”联合配送的VRP模型,并设计了一种带末端优化的模拟退火算法,以最小化总运输成本和总运输时间为目标,并解决了路径规划中的多个约束条件。

目前的VRP模型已经可以解决大规模的车辆路径规划问题,但仍有一些挑战和改进的空间。一方面,目前几乎所有的VRP模型都假定任意两个节点之间只有一条路径,没有考虑多路径的情况,然而在现实的城市路网中两个物流节点之间往往存在多条路径;另一方面,目前大多数随机VRP模型考虑的是客户需求的随机性,很少考虑车辆通行成本或时间的随机性,虽有少数的VRP模型考虑了车辆通行成本或时间的随机性,但通常假定通行成本或时间服从某种概率分布或是时间依赖的,然而在现实的城市路网中两个物流节点之间的任一路径由于受到交通拥堵、道路施工、天气状况等因素的影响具有高度的不确定性,这种不确定性一般很难利用某种概率分布进行描述。为此,本文对经典的VRP进行了新的拓展研究,考虑了任意两个物流节点之间存在多条路径且每条路径的通行成本或时间真正不确定性的情况,简称为随机多路径(stochastic multi-path vehicle routing problem,SMP-VRP),以期为第三方物流企业开展城市配送提供更加合理有效的技术支持。

1 问题描述与建模

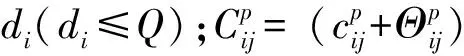
minE[f(X,Θ)]

(1)

s.t.

(2)

(3)

(4)

(5)

(6)

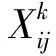
(7)

s.t.

(8)

(9)

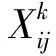
2 算法设计

VRP属于NP-hard组合优化问题,求解难度较大,可想而知SMP-VRP的求解难度更大[11]。为此,本文设计了一种具有较高求解效率的两阶段算法。为降低问题求解的复杂度,算法的第一阶段采用具有约束的K-means算法对客户进行分组,为VRP问题提供了快速的初始解,降低问题计算的时间。基于客户的分组结果,SMP-VRP可被拆分成若干个随机多路径旅行商问题(stochastic multi-path traveling salesman problem,SMP-TSP);算法的第二阶段,为解决通行成本的不确定性,先将SMP-TSP转化成等价的情景规划问题(deterministic equivalent problem,DEP),再近似成确定型规划问题(deterministic approximation problem,DAP),并加以求解。

2.1 第一阶段算法

K-means算法是目前人工智能领域常用的一种基于无监督学习的聚类算法,可以将数据集中的样本划分成若干个不相交的子集[12]。本文以配送车辆的额定载重为约束,采用具有约束的K-means算法实现对客户的分组,具体步骤如下:

1) 输入原始数据:包括每个客户的经纬度坐标、每个客户的货运需求量以及配送车辆的额定载重Q;

3) 将客户按其货运需求量从大到小降序排列;

4) 按顺序将客户逐一分配给距其最近且有剩余服务能力的质心;

5) 若所有客户均被分配,则转入步骤6),若有客户无法进行分配,则令M=M+1,返回步骤2),如此直至所有客户均完成分配;

6) 更新每个质心的坐标,即用每个质心所服务客户的经度、纬度坐标的均值代替其当前的经度、纬度坐标;

7) 重复执行步骤2)～6)若干次,返回结果,每个质心所服务的客户即为一组。

minE[g(X,Θ)]

(10)

s.t.

(11)

(12)

(13)

Xij∈{0,1},∀(i,j)∈A

(14)

(15)

s.t.

(16)

(17)

通过K-means算法,我们将客户群进行更简洁高效的聚类计算,将SMP-VRP转化为SMP-TSP,大大降低了原问题的复杂度。

2.2 第二阶段算法

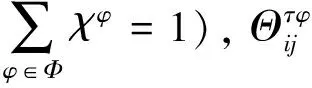
(18)

约束条件为式(11)～(14)以及

(19)

(20)

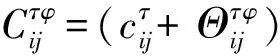
虽然DEP模型属确定型模型,但在现实中要全面划分各种交通情景非常困难,而且路径随机通行成本的概率分布也很难得知。根据Fadda等[15]的研究,在现实的城市路网中路径的随机通行成本具有明显的左尾渐进独立性,不论路径的随机通行成本服从正态分布还是耿贝尔、拉普拉斯、均匀、Logistic等常见分布,DEP模型均可近似成如下的确定型规划问题(DAP):

(21)

约束条件为式(11)～(14)。

β=7.84/(2|Tij|maxfDET/|N|-m)

(22)

式中,|Tij|max表示任意两点间路径数量的最大值;fDET表示以两点间最短路构成的确定型TSP的目标函数值;|N|表示节点的数量;m表示任意两点间最短路距离的最小值。

由于DAP模型的目标函数只体现了求解决策变量Xij的成本开销,因此SMP-TSP模型的目标函数值需通过以下的蒙特卡洛仿真步骤得到:

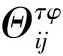
(23)

(24)

至此,通过求解每一个SMP-TSP,即可得到SMP-VRP的解。在算法的第二阶段,通过将SMP-TSP问题转化为DEP问题,再转化为DAP问题求解,大大降低了原问题的求解难度;通过蒙特卡洛仿真来近似求解DAP模型,大大提高了模型在现实交通情景中的适用性。

3 算例测试

为验证所提出的模型和算法,本文模拟京东物流在南京某一片区(如图1所示)的城市配送业务生成了5组算例,5组算例的客户数量均设为100。路网数据是通过OpenStreetMap获取的真实路网数据,任意两个物流节点之间的路径数量设为3条。京东物流在该区域的配送中心的经纬度坐标数据通过百度地图获得,客户的经纬度坐标与需求、车辆的额定载重根据调研获取的数据模拟生成,方法如下:客户的需求在[1, 100] (单位: unit)之间随机均匀产生;配送车辆的额定载重为500 unit;路网中任意两点间路径的固定通行成本为两点间最短路的长度并取整,任意两点间路径的固定通行成本的波动在其[0.5, 1]倍之间随机均匀产生。算法代码基于Python3.8编写,并调用了OSMnx、NetworkX、PyTSP等软件包,测试平台为Windows 11;具有约束的K-means算法的迭代次数设置为300次;蒙特卡洛仿真的交通情景设置为100种、迭代次数设置为10次。

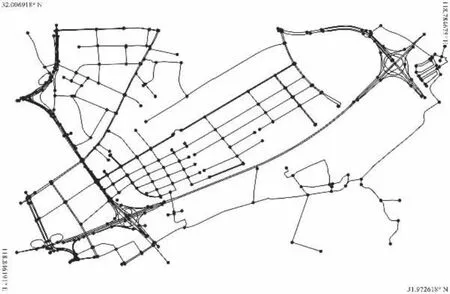
图1 所研究区域的路网图Fig.1 Road network map of the studied area

3.1 测试结果的对比分析

为验证该算法的先进性,本文模拟了京东物流的日常配送模式——基于经验的车辆路径安排,即按照最近邻域搜索算法安排车辆路径。其中,每组算例运行10次,10次结果取均值计入表中,结果如表1所示。其中,算例1求解的均值结果表现出的优越性为最好,配送成本降低约8.4%,算例5的求解结果为最低,约6.0%,其余算例的配送成本的节约则在此之间。数据表明,两阶段算法对比最近领域搜索算法能够带来7.1%的平均配送成本节约,这说明本文提出的两阶段算法比最近邻域搜索算法更具优势。

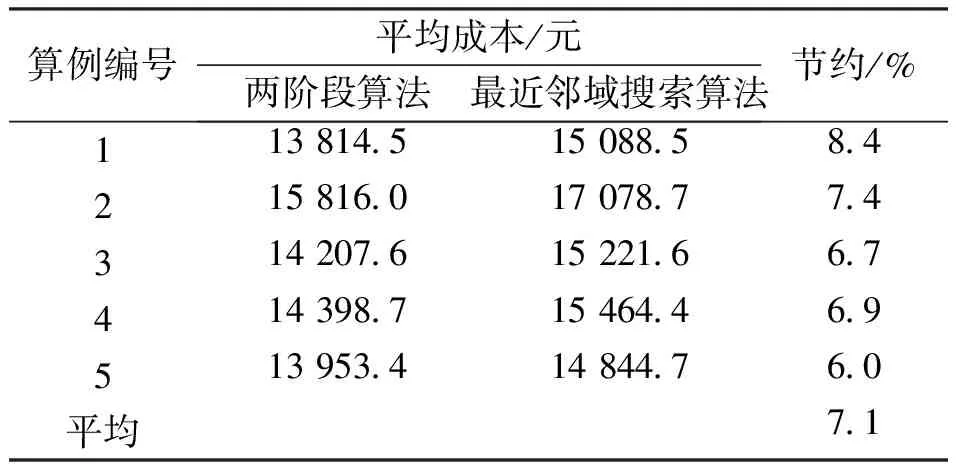
表1 基于不同组织方法的配送成本Tab.1 Distribution cost based on different organizational methods

3.2 测试结果的稳定性分析

为考察多路径对两阶段算法求解结果稳定性的影响,分别以客户节点之间路径数量为3、4、5进行运算,计算结果绘制箱线图(如图2、3、4)。5组算例在每种路径数目下各进行10次运算,将结果绘制成箱型图。根据图显示结果,整体数据没有离群点,说明数据比较均衡,没有过多的异常数据;根据图中的中位线位置分析,客户节点之间可能存在多条路径,而算例2的期望成本明显高于其他算例,这表明多路径条件下,算例计算出的期望成本取决于算例本身的组成结构。此外,其他算例的期望成本差距不大。因此,合理地选择客户进行服务可以避免高额的配送成本投入。需要注意的是,在多路径条件下,算例的组成结构会对期望成本产生较大的影响,因此在选择客户进行服务时,需要进行合理的规划和优化,才能够有效地降低配送成本并提高服务质量。图中直观地反映了每组算例求解结果的波动情况,可以看出波动较小,求解结果较为稳定,且该性质并不因为路径数目的变化而变化。

图2 路径数为3的求解质量图Fig.2 Solution quality based on 3 paths

图3 路径数为4的求解质量图Fig.3 Solution quality based on 4 paths

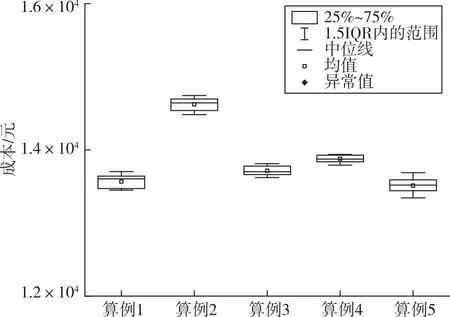
图4 路径数为5的求解质量图Fig.4 Solution quality based on 5 paths

3.3 不同路径数目对成本影响测试

为考察多路径对配送成本的影响,将计算结果取均值绘制柱状图,如图5所示。在同一组算例中,路径数为3得到的期望配送成本是最高的,路径数为5得到的期望配送成本是最低的。不难看出,随着两节点的路径数目的增加,配送成本变得越低。在现实生活中,当配送车辆在客户节点之间存在着更多的路径选择,就能做出更优的选择结果,从而更好地减少配送成本。

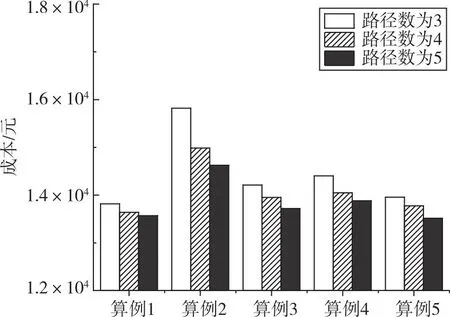
图5 不同路径数对配送成本的影响Fig.5 Impact of different numbers of paths on distribution cost

3.4 配送车辆载重对成本影响测试

本文还通过修改配送车辆的载重,来观察载重对配送成本的影响。分别选择载重为300、400、500 unit,对每组算例进行10次运算,取均值计入图中(如图6所示)。根据图中所示,随着车载的加大,配送成本显著降低。载重的调整会影响配送路径的选择和客户的分组,更大容量的载重使得配送车辆携带更多的货物,能够服务更多的客户,从而降低成本。尽量避免某些需要较多物资的客户被单独分配,这意味着需要进行多次配送,增加了成本。适当提高载重限制,可以在保证客户需求和货物配送的同时,减少配送车辆的数量和降低配送成本。

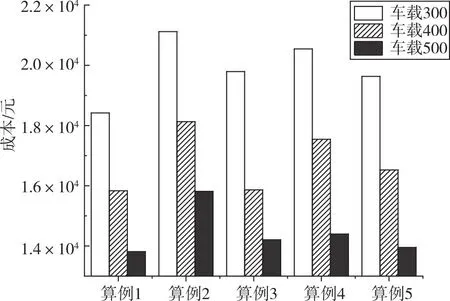
图6 载重对配送成本的影响Fig.6 Impact of capacity on distribution cost

4 结语

本文在经典VRP的基础上,考虑了配送车辆在客户节点之间路径选择的多样性,及其路径上的各种不确定的环境因素,将问题转变成随机、多路径车辆问题,建立的随机多路径VRP模型更加契合现实的城市配送运作环境。基于现实城市交通网络,考虑客户节点之间的多路径,并通过求解DAP模型解决环境因素,设计了一套两阶段算法。通过算例测试分析可以发现,本文提出的两阶段算法在SMP-VRP问题的路径规划中展现出了明显的优势,相比于基于经验的车辆路径安排,两阶段算法可以带来平均7.1%的配送成本节约;大量的测试数据显示,计算结果是稳定的,具有可靠性;通过分别改变客户节点之间的路径数量以及车载的大小,发现实验结果能很好地契合现实生活中实际情况,具有现实意义和应用价值。因此,本文提出的两阶段算法是一种可行、稳定而有效的优化配送成本的方法,可以在实际中得到更广泛的应用。