基于参数辨识的IPMSM电流谐波自适应抑制方法研究

黄于丹 杨双 李国银 赵有乾 杜超

文章编号：2096-398X2024）03-0150-08

（1.重庆中车四方所科技公司， 重庆 401133； 2.陕西科技大学 电气与控制工程学院，  陕西 西安 710021； 3.苏州伟创电气科技股份有限公司 西安分公司研发中心， 陕西 西安 710061）

摘 要：为了减小电机参数变化对电流谐波抑制效果的影响，提高谐波补偿电压的精度，提出了一种考虑参数变化的电流谐波抑制方法来抑制内置式永磁同步电机IPMSM）控制系统中的电流谐波.在电流谐波抑制方法的基础上，引入遗忘因子递推最小二乘法FFRLS）构建自适应电流谐波抑制环，通过FFRLS在线辨识IPMSM运行过程中的电机参数，并将参数变化的辨识结果引入到稳态谐波电压方程中，动态更新谐波补偿电压，从而减小了电机参数变化对谐波补偿电压产生的影响，提高了电流谐波抑制的效果.最后，仿真和实验结果验证了提出方法的正确性和有效性.

关键词：内置式永磁同步电机； 电流谐波抑制； 参数辨识

中图分类号：TM351    文献标志码： A

Research on an adaptive current harmonic suppression method based on parameter identification for interior permanent magnet synchronous motors

HUANG Yu-dan1， YANG Shuang2， LI Guo-yin1， HAO You-qian3， DU Chao2*

1.Chongqing CRRC Sifang Institute Technology Co.， Ltd.， Chongqing 401133， China; 2.School of Electrical and Control Engineering， Shaanxi University of Science & Technology， Xi′an 710021， China; 3.Xi′an Branch R & D Center， Suzhou VEICHI Electric Co.， Ltd.， Xi′an 710061， China）

Abstract：In order to reduce the influence of motor parameters variation on the current harmonic suppression and improve the accuracy of harmonic compensation voltage，a current harmonic suppression method considering parameters variation is proposed to suppress the current harmonic for interior permanent magnet synchronous motors IPMSM） control system in this paper.Based on the current harmonic suppression method，a forgetting factor recursive least square method FFRLS） is introduced to build an adaptive current harmonic suppression loop.The FFRLS can identify the IPMSM parameters，and the identification results of parameters variation are introduced into the steady-state harmonic voltage equation to dynamically update the harmonic compensation voltage.Therefore，the influence of motor parameters variation on the harmonic compensation voltage generation is reduced，and the effect of current harmonic suppression is improved.Finally，the effectiveness of the proposed method is verified by the simulation and experimental results.

Key words：interior permanent magnet synchronous motors； current harmonic suppression； parameters identification

0 引言

内置式永磁同步电动机（IPMSM）具有功率密度高、调速性能好、结构紧凑等优点，在工业领域和新能源汽车领域得到了广泛的应用［1］.

然而，在IPMSM控制系统中，由于死区效应和电力电子器件导通管压降引起的逆变器的非线性特性，会在定子电流中引入时间谐波.同时，由于齿槽效应和磁饱和效应，定子电流中还含有空间谐波［2，3］.电流谐波会产生转矩脉动和转速波动，使系统的控制性能变差［4，5］，降低了IPMSM控制系统的可靠性和稳定性，严重制約了IPMSM在高精度控制领域的应用［6］.因此，有必要对IPMSM控制系统中的电流谐波进行抑制.

对于由逆变器非线性特性引起的时间谐波，采用的是通过补偿谐波分量来优化电机控制的方案.在文献［7，8］中，谐振控制器与比例积分调节器（PI）并联使用，以减少定子电流的畸变.在文献［9］中，矢量谐振控制器与无差拍电流预测控制（DPCC）的并联使用以补偿交流扰动，特别是由交流扰动引起的电流谐波.在文献［10，11］中，采用重复控制（Repetitive Control，RC）对周期性的谐波干扰信号进行抑制.在文献［12］中，在对谐波特性分析的基础上，将复矢量PI控制器用于电流谐波的抑制.在文献［13］中，使用自抗扰控制器取代传统PI控制器，通过补偿系统扰动的方式抑制谐波的产生.文献［14，15］提出了一种基于多重同步旋转坐标系变换（MSRFTs）的电流谐波抑制方法，在该方法中，需要电感和定子电阻的值来构建电流谐波抑制环.然而，在IPMSM实际运行过程中，电机参数是实时变化的［16，17］，因此该方案的电流谐波抑制效果会受到影响.

为了减小IPMSM参数变化对电流谐波抑制方法的影响，本文提出一种基于遗忘因子递推最小二乘法（FFRLS）的电流谐波抑制方法，构建自适应电流谐波抑制环路.通过FFRLS辨识电机参数并将辨识结果引入至自适应谐波抑制环，提高了谐波补偿电压的精度和电流谐波抑制效果.仿真和实验结果验证了所提方法的有效性.

1 IPMSM的谐波模型

IPMSM系统具有非线性、多变量和强耦合的特点，为了便于分析，将IPMSM三相数学模型变换到dq坐标系下，忽略暂态分量，IPMSM稳态电压方程如下：

ud=Rsid－ωLqiq

uq=Rsiq+ωLdid+ωψf（1）

式（1）中：ud，uq分别为d，q轴电压分量; id，iq分别为d、q轴电流分量; Ld，Lq分别为d、q轴电感分量; Rs为定子电阻; ω为电角速度; ψf为永磁体的磁链值.

在实际电机控制系统中，IPMSM的定子绕组主要采用星形连接，理想条件下绕组对称分布，绕组的反电动势波形不含偶次谐波.因此，三相定子电流的主要谐波成分为5次、7次、11次和13次谐波，其中5次和7次谐波含量最多.考虑谐波分量时，电机的三相定子电流可表示为：

ia=i1sinωt+θ1）+i5thsin－5ωt+θ2）+[DW]i7thsin7ωt+θ3）

ib=i1sinωt+θ1－2π3）+i5thsin－5ωt+θ2－2π3）+i7thsin7ωt+θ3－2π3）

ic=i1sinωt+θ1－4π3）+i5thsin－5ωt+θ2－4π3）+i7thsin7ωt+θ3－4π3）（2）

式（2）中：i1、i5th、i7th分别为基波电流、五次和七次谐波电流的幅值; θ1、θ2、θ3分别为基波电流、5次和7次谐波电流的初始相位角.

在恒幅值约束条件下，将三相定子电流变换到dq坐标系下：

id=id1+i5thcos－6ωt+θ5）+i7thcos6ωt+θ7）

iq=iq1+i5thsin－6ωt+θ5）+i7thsin6ωt+θ7）（3）

式（3）中：id1和iq1分别为基波电流的d、q轴分量.θ5和θ7分别为5次和7次谐波电流的初始相位角.

2 电流谐波抑制方法

电流谐波抑制方法由电流谐波提取和谐波补偿电压计算两部分组成.

2.1 电流谐波提取

由方程3）可知，在dq坐标系下，基波电流为直流分量，谐波电流为交流分量.同理，dq坐标系下的谐波分量在旋转频率与谐波电流相同的坐标系下可以转换为直流分量.IPMSM的多重同步旋转坐标系如图1所示.

图1中，αβ坐标系为静止坐标系; dq坐标系以ω的速度与转子同步旋转; dq7th坐标系以7ω的速度与dq坐标系同向旋转; dq5th坐标系以5ω的速度与dq坐标系反向旋转.dq坐标系与谐波坐标系的变换矩阵如下所示：

Tdq→dq5th=cos6ωt）－sin6ωt）sin6ωt）cos6ωt）（4）

Tdq→dq7th=cos6ωt）sin6ωt）－sin6ωt）cos6ωt）（5）

根据上述分析，谐波电流提取模型如图2所示，通过坐标变换和低通滤波器（LPF）提取三相电流中的5、7次谐波分量.

图2中，id5th、iq5th分别为dq5th坐标系下5次谐波电流的d、q轴分量; id7th、iq7th分别为dq7th坐标系下7次谐波电流的d、q轴分量.

2.2 谐波补偿电压的计算

由于IPMSM的齿槽效应，永磁体磁链中会引入高次分量，但由于其含量较小，可以忽略不计.将式（3）代入IPMSM稳态电压方程，可以得到dq坐标系下含谐波分量的电压方程：

ud=Rsid1－ωLqiq1+5ωLqi5thsin－6ωt+θ5）+Rsi5thcos－6ωt+θ5）－7ωLqi7thsin－6ωt+θ7）+Rsi7thcos－6ωt+θ7）+…uq=Rsiq1+ωLdid1+ωψf－5ωLdi5thcos－6ωt+θ5）+Rsi5thsin－6ωt+θ5）+7ωLdi7thcos6ωt+θ7）+Rsi7thsin6ωt+θ7）+…（6）

将式（6）由dq坐标系变换到5次谐波坐标系.在dq5th坐标系下电压方程可以表示为：

ud=Rsid1cos－6ωt+θ4）－ωLqiq1sin－6ωt+θ4）+5ωLqiq5th+Rsid5th－7ωLqi7thsin12ωt+θ6）+Rsi7thcos12ωt+θ6）+…uq=Rsiq1sin6ωt+θ4）+ωLdid1cos6ωt+θ4）+ωψfcos－6φ1）－5ωLdid5th+Rsiq5th+7ωLdi7thcos12ωt+θ6）+Rsi7thsin12ωt+θ6）+…（7）

式（7）中：θ4、θ6、φ1分別为dq5th坐标系下基波电流、7次谐波电流和永磁体磁链的初始相位角.

在dq5th坐标系下，基波电流和7次谐波电流为交流分量，5次谐波电流为直流分量.忽略交流分量，5次谐波坐标系下的稳态谐波电压方程为：

ud5=Rsid5th+5ωLqiq5th

uq5=Rsiq5th－5ωLdid5th（8）

式（8）中：ud5和uq5分别为dq5th坐标系下5次谐波电压的d、q轴分量.

同理，将式（6）由dq坐标系变换到7次谐波坐标系.忽略交流分量，7次谐波坐标系下的稳态谐波电压方程为：

ud7=Rsid7th－7ωLqiq7thuq7=Rsiq7th+7ωLdid7th（9）

式（9）中：ud7、uq7分别为dq7th坐标系下7次谐波电压的d、q轴分量.

根据5次和7次稳态谐波电压方程，设计了具有交叉积项的PI调节环节，有效地抵消了耦合成分对控制的影响.5次和7次谐波补偿电压计算示意图如图3所示.针对5次和7次谐波电流，分别以i*d5/7th= 0和i*q5/7th=0作为控制目标.谐波补偿电压ud5/7th由带交叉积项的PI调节器的输出电压与谐波电压Δud5/7相加得到;谐波补偿电压uq5/7th由带交叉积项的PI调节器的输出电压与谐波电压Δuq5/7相加得到.

2.3 电流谐波抑制方法的稳定性分析

为了分析谐波电流抑制方法的稳定性，以5次谐波电流的抑制为例，将闭环谐波电流抑制的系统框图简化，如图4所示.

根据图4可以得到的5次电流谐波在d、q轴的传递函数表达式：

id5th=Rs1+kp1+ki1spwmTpwms+1）Lds+Rs）1+Rs1+kp1+ki1spwmTpwms+1）Lds+Rs）id5th+5ωLq1+kp2+ki2spwmTpwms+1）Lds+Rs）1+Rs1+kp1+ki1spwmTpwms+1）Lds+Rs）Δiq5th（10）

5次諧波电流在d、q轴闭环特征方程为：

Ds）=TpwmLds3+TpwmRs+Ld）s2+pwmRskp1+pwmRs+Rs）s+pwmRski1=0（11）

Ds）=TpwmLqs3+TpwmRs+Lq）s2+pwmRskp2+pwmRs+Rs）s+pwmRski2=0（12）

根据三阶系统的劳斯稳定性判据，5次谐波电流抑制的稳定性条件为：

pwmTpwmRs+pwmLd+pwmTpwmRskp1+Ld>pwmTpwmLdki1（13）

pwmTpwmRs+pwmLq+pwmTpwmRskp2+Lq>pwmTpwmLqki2（14）

通过相似的分析，7次谐波电流抑制的稳定性条件为：

pwmTpwmRs+pwmLd+pwmTpwmRskp3+Ld>pwmTpwmLdki3（15）

pwmTpwmRs+pwmLq+pwmTpwmRskp4+Lq>pwmTpwmLqki4（16）

式（15）、（16）中：kp3、kp4和ki3、ki4分别为i*q7th和 i*d7th的PI调节器的比例系数和积分系数.

3 基于FFRLS的IPMSM电流谐波抑制方法

谐波补偿电压的准确程度取决于谐波补偿电压计算中所使用的电机参数.IPMSM的参数变化会导致谐波补偿电压的生成出现误差，降低了谐波电流的抑制效果，因此在电流谐波抑制方法的基础上引入FFRLS，在线辨识Rs、Ld、Lq 以及ψf 的值.FFRLS的参数辨识模型为：

yk）=φTk）[Aθ^]k）+εk）[Aθ^]k）=[Aθ^]k－1）+k）［yk）－φTk）[Aθ^]k－1）］

Pk）=1λ［I－k）φTk）］Pk－1）（17）

式（17）中：yk）为系统输出矩阵，k）为系统输入矩阵，[Aθ^]k）为待识别的参数矩阵，λ为遗忘因子，Pk）为协方差矩阵，εk）为噪声信号矩阵，k）为增益矩阵，I为单位矩阵.

考虑暂态分量，IPMSM在dq坐标系下的电压方程为：

ud=Rsid+Lddiddt－ωLqiq

uq=Rsiq+Lqdiqdt+ωLdid+ωψf（18）

经过离散化后，dq坐标系下IPMSM的电压方程可表示为：

udk）=Rsidk）+Ldk）idk）－idk－1）T－ωLqk）iqk）

uqk）=Rsiqk）+Lqk）iqk）－iqk－1）T+ωLdk）idk）+ωψf（19）

为保证参数辨识模型的满秩，同时避免矩阵运算，减少计算量，避免Ld与Lq辨识的耦合问题，d、q轴电感辨识的数学模型如下所示：

uqk）－Rsiqk）－Lqiqk）－iqk－1）T－ωψf=ωidk）Ldk）+ε1k）（20）

udk）－Rsidk）－Ldidk）－idk－1）T=－ωiqk）Lqk）+ε2k）（21）

式（20）、（21）中：ε1k）和ε2k）为噪声信号，φ1k）=ω，[Aθ^]1k）=Ldk），φ2k）=－ωiqk），[Aθ^]2k）=Lqk），y1k）=uqk）－Rsiqk）－Lqiqk）－iqk－1）T－ωψf， y2k）=udk）－Rsidk）－Ldidk）－idk－1）T.

定子电阻和永磁体磁链辨识的数学模型如下所示：

uqk）－ωLdk）idk）－Lqiqk）－iqk－1）T－ωψf=iqk）Rs+ε3k）（22）

uqk）－ωLdk）idk）－Lqiqk）－iqk－1）T－Rsiqk）=ωψf+ε4k）（23）

式（22）、（23）中：ε3k）和ε4k）为噪声信号，φ3k）=iqk），[Aθ^]3k）=Rs，φ4k）=ω，[Aθ^]4k）=ψf，y3k）=uqk）－ωLdk）idk）－Lqiqk）－iqk－1）T－ωψf， y4k）=uqk）－ωLdk）idk）－Lqiqk）－iqk－1）T－Rsiqk）.

首先辨识d、q轴的电感值，然后将辨识出的电感值引入式23）和式24）中辨识定子电阻和永磁体磁链的值.基于FFRLS的电流谐波抑制方法如图5所示.

为了抑制IPMSM控制系统的电流谐波，消除参数变化对谐波抑制效果的影响，在FFRLS参数辨识的基础上建立自适应电流谐波抑制环.FFRLS识别电机参数的变化，并将辨识出的参数引入电流谐波抑制环中.然后，通过FFRLS对稳态谐波电压方程中使用的电机参数进行更新，并得到修正后的谐波补偿电压.最后，通过矩阵T-1dq→dq5th和T-1dq→dq7th将谐波补偿电压变换为ud_fc和uq_fc，并注入相对应的d、q轴当中去抑制三相电流中的谐波分量.

4 仿真结果与分析

为了验证所提出方法的有效性，在MATLAB/Simulink中进行了仿真验证.通过设定逆变器死区时间和管压降，在三相电流中引入谐波分量.仿真中，为系统加10 N·m的负载，电机给定转速为600 r/min.电机仿真模型的主要参数如表1所示.

4.1 参数不变时电流谐波抑制方法

分别在传统电机控制和具有电流谐波抑制的矢量控制下进行仿真，仿真结果如图6和图7所示.采用电流谐波抑制算法后，A相电流波形的正弦度得到明显改善，其中总谐波畸变THD）由10.65%降低到1.46%，5次谐波的含量由7.44%降低到0.96%，7次谐波的含量由7.62%降低到0.87%.

综上所述，在电机参数恒定的情况下，通过电流谐波抑制算法，有效降低了 A相电流的畸变，并抑制了5、7次谐波电流.

4.2 参数变化时的电流谐波抑制方法

4.2.1 IPMSM电机参数变化对谐波抑制效果的影响

在IPMSM实际运行过程中，电机参数是实时变化的.为了模拟电机实际运行过程中参数的变化，在1.2 s時，d轴电感从0.921 5 mH增加到1.1 mH，q轴电感从1.018 mH增加到1.2 mH，定子电阻从0.11 Ω增加到 0.16 Ω，永磁体磁链从0.111 9 Wb减少到0.09 Wb.当电机参数发生变化时，没有参数辨识的电流谐波抑制方法的仿真结果如图8所示.与图7的结果相比，虽然采用了电流谐波抑制方法，但5次谐波含量从0.96%增加到1.91%，7次谐波含量从0.87%增加到0.93%.

结果表明，随着IPMSM参数的变化，5、7次谐波的含量增加.因此，有必要考虑IPMSM参数变化对电流谐波抑制效果的影响.

4.2.2 基于FFRLS的IPMSM参数辨识

在1.2 s时，IPMSM参数如上文所述发生变化，电机参数的辨识结果如图9所示.定子电阻的最终辨识值为0.159 5 Ω，辨识的相对误差为0.31%；永磁体磁链的最终辨识值为0.090 2 Wb，辨识的相对误差为0.22%；d轴电感的最终辨识值为1.11 mH，辨识的相对误差为0.91%；q轴电感的最终辨识值为1.198 mH，辨识的相对误差为0.17%.

结果表明，FFRLS具有精度高、稳定性好、收敛速度快等优点.当IPMSM参数发生变化时，FFRLS可以快速跟踪电机参数的变化，实现对IPMSM参数的准确辨识.

4.2.3 基于FFRLS的IPMSM电流谐波抑制方法

当电机参数如上文所述变化时，基于FFRLS的电流谐波抑制方法的仿真结果如图10所示.与图8的结果相比，总谐波畸变THD）从2.02%降低到0.44%，5次谐波含量从1.91%降低到0.12%，7次谐波含量从0.93%降低到0.25%.

综上所述，当IPMSM参数发生变化时，仿真结果表明，基于FFRLS的电流谐波抑制方法可以有效地降低5、7次谐波含量，提高了电流谐波抑制效果.

5 实验结果与分析

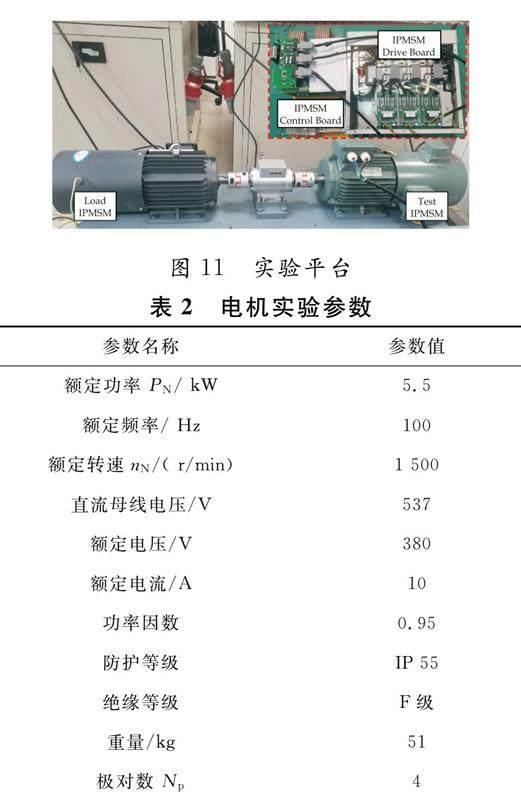
为了进一步验证所提方案在实验的情况下对谐波抑制的有效性，采用如图11所示的对拖实验平台对所提方案进行实验验证，电机实验的主要参数如表2所示.

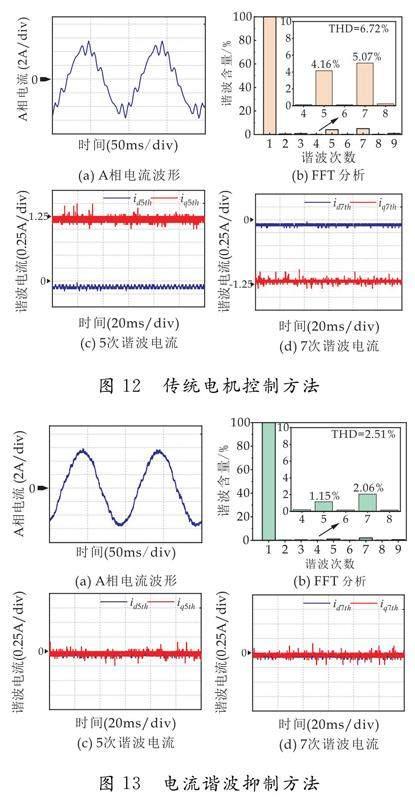
5.1 参数不变时电流谐波抑制方法有效性验证

在实验中，为系统加15 N·m负载，电机给定转速为75 r/min.在电机参数不发生变化时，采用谐波电流抑制方法和不采用谐波电流抑制方法的矢量控制策略的实验结果如图12和图13所示.与不具有谐波电流抑制方法的电机控制的结果相对比，具有谐波电流抑制方法的A相电流的总谐波畸变THD）从6.72%降低到2.51%，5次谐波含量从4.16%降低到1.15%，7次谐波含量从5.07%降低到2.06%.

实验结果表明，采用电流谐波抑制算法后，A相电流波形的正弦度得到明显改善，其中总谐波畸变THD）降低.综上所述，在不考虑电机参数变化的情况下，通过电流谐波抑制算法，可有效降低电流的畸变，可有效减少了5、7次谐波电流分量.

5.2 参数变化时基于FFRLS的电流谐波抑制方法有效性验证

在电机参数发生变化时，不具有参数辨识和具有FFRLS参数辨识的电流谐波抑制方案的实验结果分别如图14和图15所示.与不具有FFRLS参数辨识的谐波抑制结果相对比，具有FFRLS参数辨识方案的总谐波畸变THD）从5.95%降低到2.84%，5次谐波含量从3.42%降低到1.40%，7次谐波含量从4.55%降低到2.25%.

实验结果表明，在电机实际工作中，基于FFRLS的电流谐波抑制方法可以有效地降低电机参数变化对谐波抑制效果的影响，提高谐波抑制的准确性.

6 结论

为了降低IPMSM参数变化对电流谐波抑制效果的影响，在电流谐波抑制方法的基础上，引入FFRLS构建自适应电流谐波抑制环.FFRLS可以在线辨识IPMSM的参数变化，并将辨识结果引入到电流谐波抑制环节，从而降低了电机参数变化对谐波抑制效果的影响，提高了谐波抑制的准确性.仿真和实验结果表明，基于FFRLS的电流谐波抑制方法能有效提高电流谐波抑制的效果、减少电流谐波含量.

参考文献

［1］ 赵学铭.基于改进无位置传感器的永磁同步电动机全速域控制策略研究［D］.郑州：郑州大学，2022.

[LL]  ［2］ Liu J，hang Y.Current pulsation suppression method based on power current closed-loop control for a PMSM under fluctuating DC-link voltage.IEEE Transactions on Power Electronics，2022，371）：761-770.

［3］ 朱 元，陈冠行，肖明康，等.基于LMS自适应滤波器的PMSM谐波抑制方法.微特电机，2023，513）：1-6.

［4］ 宋若宸.死區时间优化的永磁同步电机改进多步模型预测电流控制［D］.西安：西安理工大学，2023.

［5］ 冷云贵.基于谐波电流补偿法的永磁同步电机转矩脉动抑制研究［D］.重庆：重庆理工大学，2022.

［6］ im H，Han Y，Lee ，et al.A sinusoidal current control strategy based on harmonic voltage injection for harmonic loss reduction of PMSMs with non-sinusoidal Back-EMF.IEEE Transactions on Industry Applications，2020，566）：7 032-7 043.

［7］ 魏艺涵，罗 响，朱 莉，等.基于比例谐振控制器的高凸极率永磁同步电机电流谐波抑制策略研究.中国电机工程学报，2021，417）：2 526-2 538.

［8］ 陈 哲，张序轩，刘春强，等.基于比例谐振型自抗扰控制的永磁同步电机电流解耦及谐波抑制策略研究.中国电机工程学报，2022，4224）：9 062-9 072.

［9］ Tian M，Wang B，Yu Y，et al.Static-errorless deadbeat predictive current control for PMSM current harmonics suppression based on vector resonant controller.IEEE Transactions on Power Electronics，2023，384）：4 585-4 595.

［10］ 张巧芬，刘彦呈，郭昊昊，等.用于永磁同步电机周期性转速脉动抑制的重复控制.控制理论与应用，2022，393）：432-440.

［11］ 陈 瑶，张钊源，冯鑫鹏，等.基于复合控制的永磁同步电机电流谐波抑制策略.电机与控制应用，2022，497）：30-37.

［12］ 苏锦智，张继鹏，安群涛.基于频率自适应复矢量PI控制器的PMSM电流谐波抑制策略.电机与控制应用，2021，4812）：30-36.

［13］ 王淑旺，夏麒翔.基于自抗扰的永磁同步电机谐波抑制策略.汽车技术，20209）：21-26.

［14］ Wang W，Liu C，Liu S，et al.Current harmonic suppression for permanent-magnet synchronous motor based on chebyshev filter and PI pontroller.IEEE Transactions on Magnetics，2021，572）：1-6.

［15］ 于慎波，薛镜武，夏鹏澎，等.利用谐波注入法改善永磁同步电机的运动特性.机械设计与制造，202111）：79-82.

［16］ 史婷娜，刘 华，陈 炜，等.考虑逆变器非线性因素的表贴式永磁同步电机参数辨识.电工技术学报，2017，327）：77-83.

［17］ Liu ，Wei H，Li X，et al.Global identification of electrical and mechanical parameters in PMSM drive based on dynamic self-learning PSO.IEEE Transactions on Power Electronics，2018，3312）：10 858-10 871.

【责任编辑：陈 佳】

基金项目：中国博士后科学基金面上项目（2022M712931）； 中国博士后特别资助基金项目（2023T160603）； 重庆市技术创新与应用示范专项-产业类重点研发项目（cstc2018jszx-cyzd0115）

作者简介：黄于丹（1990—），女，重庆人，中级职称，研究方向：城市轨道交通车辆控制技术

通讯作者：杜 超（1991—），男，陕西西安人，讲师，博士，研究方向：永磁同步电机控制，duchaoworkhard@163.com