基于差动电流与分布电容电流比值的直流线路纵联保护方案

2024-05-18褚倍钰李海锋彭光强梁远升

电力系统自动化 2024年9期

褚倍钰，李海锋，彭光强，梁远升，王钢

（1.华南理工大学电力学院，广东省广州市 510641；2.中国南方电网有限责任公司超高压输电公司电力科研院，广东省广州市 510663）

0 引言

高压直流输电系统由于具有传输容量大、输电距离远、线路损耗低等优点，已经被广泛应用于远距离大容量输电，但换相失败是其面临的主要问题［1-3］。相比之下，基于电压源型换流器的柔性直流输电系统不存在换相失败的问题，但造价高、运行损耗大［4-6］。近年来，新兴的多端混合高压直流输电系统采用电网换相换流器（line commutated converter，LCC）作为功率集中输送端、多个模块化多电平换流器（modular multilevel converter，MMC）作为多落点受端，综合了常规直流和柔性直流的优点，是直流输电技术发展的重要方向之一［7-9］。

由于直流输电线路大多为架空线路，故障发生概率高，故障电流上升速率大，直流线路保护作为直流输电中的关键技术一直受到广泛关注［10］。多端混合高压直流输电系统运行方式灵活多变，以三端系统为例，既可以三端方式运行，也可采用不同组合的双端运行方式。由于拓扑结构更加复杂，多端混合高压直流输电线路发生故障后要求保护能够快速准确地定位故障区域，实现故障线路区段的有效隔离，以保证系统剩余部分继续正常运行。现有多端混合高压直流输电线路保护大多沿用传统高压直流输电线路的保护方法，但这些方法仍然存在一些问题需要解决。

根据文献［11］，基于直流电压变化率的线路主保护方法，在150 Ω 的过渡电阻下灵敏性不足。而基于行波的线路主保护方法，虽然提高了耐过渡电阻能力，但是往往需要依赖于边界元件［12-14］。当限流电抗器的数值较小、对高频电气量行波的衰减较弱时，会影响行波保护的耐过渡电阻能力，可能达不到保护的预期效果［15］。

为了让线路保护方案能在高阻故障下可靠识别故障，后备保护的耐过渡电阻能力必须得到保证。现有实际工程的后备保护往往采用电流差动保护。但电流差动保护在长距离输电线路中受分布电容的影响较大，在区外故障下容易受到分布电容电流的影响而超过整定值，造成保护误动［16-17］。因此，电流差动保护往往需要通过保护延时来避开分布电容放电的暂态过程，从而降低了保护的速动性。已有改进的电流差动保护方法在一定程度上消除了分布电容电流对差动电流的影响。文献［18-19］分别基于直流线路的频变模型、分布参数模型计算线路保护整定点处电流，但计算复杂；文献［20-21］基于低通滤波后的电压呈线性分布这一特征，对沿线分布电容电流进行计算，实现了分布电容电流的补偿，但所提保护原理对双端通信实时性要求极高，当线路两侧出现毫秒级的同步误差时，保护可能发生误动。此外，这些保护的故障识别判据仍然沿用了传统电流差动保护的思路，即利用差动电流的大小进行故障判别，在整定上仍需躲过区外金属性故障下的最大不平衡电流值。由于在区内故障时，差动电流的大小受过渡电阻影响明显，保护方案的灵敏性仍将受到过渡电阻的影响。

针对上述问题，本文以三端混合高压直流输电系统为对象，在讨论分析差动电流与电容电流比值的故障特征的基础上，利用差动电流与电容电流的比值识别区内外故障。通过平均值法提取差动电流和分布电容电流的故障特征，进而提出了一种基于差动电流与分布电容电流比值的纵联保护方法。最后，基于PSCAD/EMTDC 仿真模型对所提保护方案性能进行了详细的验证与分析。

1 直流线路故障暂态特性分析

三端混合高压直流输电系统的示意图如图1 所示。该系统由1 个LCC 换流站、2 个MMC 换流站以及两条直流输电线路L1、L2组成。在LCC 出口直流母线处配备平波电抗器和直流滤波器，在MMC 出口直流母线处配备限流电抗器。在直流线路L1两侧安装保护测点a、b，在直流线路L2两侧安装保护测点d、e。图1 画出了系统的典型故障点:f1为线路L1故障，f2为线路L2故障，Fout1为整流侧区外故障，Fout2为逆变侧区外故障。本文以直流线路L1为例来讨论线路的故障特征。对直流线路L1而言，发生f1故障时为区内故障，发生f2、Fout2故障时为区外故障，发生Fout1故障时为反向区外故障。设电流正方向为换流器阀侧流向直流线路侧。

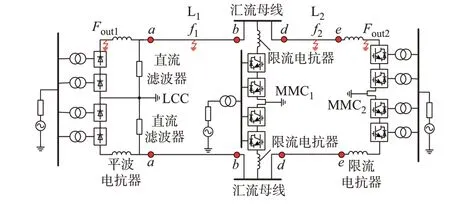
图1 三端混合高压直流输电系统示意图Fig.1 Schematic diagram of three-terminal hybrid high-voltage DC transmission system

1.1 区外故障特征分析

长距离直流输电线路发生故障时，由于线路电压的快速下降，将造成线路分布电容放电。因此，在分析线路故障暂态特征时需要考虑线路分布电容电流的影响。

以发生Fout1故障为例进行区外故障特征分析，故障附加电路如图2 所示。图中:Zp为边界元件等效阻抗；Za为测点a背侧等效阻抗；Zb为测点b背侧等效阻抗；ia（t）和ib（t）分别为t时刻测点a、b处的线路电流；if（t）为故障支路电流；ic（x，t）为线路分布电容电流，其中，x为距离测点a的距离；L为线路的长度。

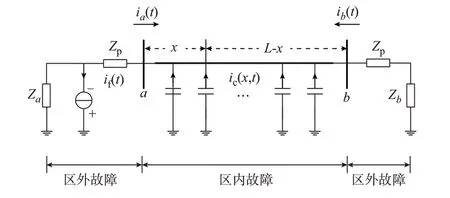
图2 区外故障下的故障附加电路图Fig.2 Superimposed circuit diagram under external fault

根据图2，由基尔霍夫电流定律（KCL）可得:

差动电流与分布电容电流的比值k满足下式:

1.2 区内故障特性分析

直流线路L1发生区内故障时，其故障附加电路如图3 所示。

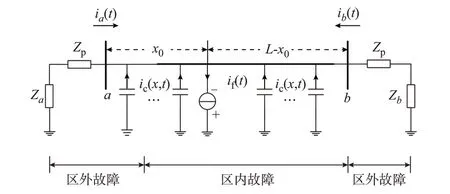
图3 区内故障下的故障附加电路图Fig.3 Superimposed circuit diagram under internal fault

由图3 可知，此时根据KCL 定理，有

由式（5）可以看出，区内故障下差动电流除了包含线路分布电容电流以外，还包含了故障支路电流，由于短路电流较大，故障支路电流往往远大于线路分布电容电流，有

差动电流与分布电容电流的比值则满足下式:

1.3 区内外故障特征差异

综上所述，当直流输电线路发生区内外故障时，差动电流与线路分布电容电流的比值k存在明显差异。发生区外故障时，k=1；发生区内故障时，k＞1。因此，可以利用上述特征进行区内外故障识别。

2 故障暂态特征提取

2.1 线路分布电容电流的估算

如何获取直流线路的分布电容电流是利用k值进行故障判别的关键所在。单位长度的分布电容电流可以通过线路电压突变量计算得到:

式中:u（x，t）为线路分布电压；C0为单位长度的线路对地电容。

由此可得直流线路总的分布电容电流为:

然而，精确获取线路上暂态分布电压比较困难。因此，为了简便计算，本文在基于线路分布参数模型分析线路故障特性的基础上，应用输电线路等传变原理［17-18］，即引入低通滤波环节对线路上电气量的频率进行限制，此时线路分布电压可近似视为线性分布，有

式中:u（0，t）、u（L，t）分别为线路两侧电压。

2.1.1 区外故障

当线路发生区外故障时，将式（10）代入式（9），即可得到低频故障特征下的电容电流简化计算方法为:

该计算方法是分布参数模型在足够低的低通滤波下的近似线性化的处理，其本质上仍然满足原分布参数模型的相互关系，是分布参数模型在低频故障特征下的一个特殊化形式，其在形式上和用pi 参数模型推导的结果类似。利用式（11），只需获取线路两侧电压即可较为准确地估算出区外故障下的分布电容电流。

2.1.2 区内故障

当线路发生区内故障时，故障点将故障线路分为两段，两段线路的线路电压均可视为线性分布，而且满足如式（10）所示的关系。此时，区内故障下的线路分布电容电流为:

式中:u（lf，t）为故障点处电压；lf为故障点距a点距离。

由于在实际工程中，直流线路上的故障点电压难以获取，无法直接利用式（12）进行计算。若同样利用式（11）来计算区内故障下的线路分布电容电流之和，则与利用式（12）的准确计算之间存在以下关系。

考虑到相比线路两侧，故障点处压降将更大，则有:

结合式（11）和式（12），可得:

由式（14）可知，区内故障时，利用式（11）计算得到的分布电容电流之和将小于式（12）所对应的实际值。进一步将其代入比值k进行分析，则有:

由此可见，采用式（11）对区内故障下线路分布电容电流进行近似计算并不会影响区内故障的故障特征。

2.2 低通滤波截止频率的选择

由1.2 节的分析可知，区内故障下的差动电流等于故障支路电流与线路分布电容电流的差。设故障初始阶段故障支路电流和线路分布电容电流的方向均不变，二者的数值均为正数，且if（t）＞ic（t），则差动电流与线路分布电容电流的比值k可以表示为:

对于故障支路电流，当过渡电阻Rf较大时，线路电压虽然有所降低，但压降较小，此时if可以近似表示为:

式中:kv为电压降系数；UN为线路额定电压。

而线路分布电容电流则与线路电压突变量有关，线路电压突变量的大小又与电压谐波分量的角频率有关。设低通滤波截止角频率为ωc，则滤波后沿线电压的谐波角频率最大为ωc。为了讨论线路分布电容电流最大的情况，设u(x，t)=Uxsin(ωct+φx)，Ux和φx分别为沿线电压的幅值和相位，沿线电压变化率为:

由于故障期间线路电压将发生跌落，有Ux≤UN，再将式（18）代入式（11）中，有

取ic（t）的最大值，再将ic（t）、if（t）代入式（16）中，有

要使区内故障下的k值大于1，则要满足:

根据式（21）可以确定低通滤波的截止频率。由式（21）可见，在线路长度确定的情况下，考虑的过渡电阻越大（对应保护的灵敏性越高），低通滤波器的截止频率需要取更低的值。

以昆柳龙三端混合高压直流输电工程系统参数为例:线路L1长度为932 km，线路单位长度电容C0为1.60×10-11F/m，kv为0.9，过渡电阻Rf为600 Ω，则可得截止频率fc＜8.01 Hz；若过渡电阻Rf为400 Ω时，则可得截止频率fc＜12.01 Hz。

2.3 k 值的计算

式（11）的线路分布电容电流也可以写为:

式中:Δt为采样时间间隔；ua（j）、ub（j）分别为低通滤波后的线路a、b端电压j点采样值。

差动电流有:

式中:ia（j）、ib（j）分别为低通滤波后的线路a、b端电流j点采样值。

用|iab|、|ic|一段时间内的平均值来提取故障特征，有

式中:N为时间窗内的采样点个数。

进行平均值处理后的差动电流与线路分布电容电流的比值为:

区外故障时kave=1；区内故障时kave＞1。相较于只利用某一采样点的故障特征，通过平均值提取故障特征的方式利用了一段时间内的故障信息，具有更高的可靠性。

3 线路保护方案设计

3.1 启动单元

由于直流线路发生故障时，会引起极线电压的快速下落，可以利用极线电压行波的变化作为保护的启动单元:

式中:ΔU为极线电压行波变化量；U(j)为极线电压行波j点采样值；ΔUset为启动判据；Uref为额定线电压；k0为电压变化系数。

保护启动判据阈值的整定原则为:应大于正常运行下电压变化量的最大值ΔUmax、小于线路故障时电压变化量的最小值ΔUmin，并保证保护启动的灵敏性。根据实际工程昆柳龙三端混合高压直流输电系统，直流线路正常运行状态下的ΔUmax为0.02Uref，再通过昆柳龙三端混合高压直流输电系统的电磁暂态仿真获取ΔUmin为0.09Uref，考虑一定的裕度，故将k0取为0.08，ΔUset设为0.08Uref。

3.2 故障识别与选极单元

结合上文分析，利用平均值处理后的差动电流与线路分布电容电流的比值构造故障识别判据如下:

式中:kave，φ为差动电流与线路分布电容电流的比值，φ=p，n，分别表示直流线路正、负极电气量；kset为线路保护整定值。

在判据整定上，令kset=krel×1，krel为可靠系数，取1.2～2.0。由于利用的是线路极线电气量，所提判据除了能识别区内外故障外，还带有故障选极的效果，选极判据如下:

当识别线路故障为正极故障时，正极保护装置动作；当识别线路故障为负极故障时，负极保护装置动作；当识别线路故障为极间故障时，正、负极保护装置一起动作。

利用差动电流与电容电流的比值构成故障识别判据，本质上是利用差动电流与分布电容电流的相对大小识别区内外故障。由于差动电流和分布电容电流的数值都会随着过渡电阻的增大而减小，采用差动电流与分布电容电流的比值作为判据，可以削弱过渡电阻对判据的影响，提高保护的灵敏性。同时，相比其他相关保护方法，所提判据的整定原则也更简单可靠。区外故障下差动电流与电容电流的比值等于1，区内故障下差动电流与电容电流的比值大于1，判据的整定仅需要在此基础上再考虑可靠系数，无须进行电磁暂态仿真。

4 保护判据性能仿真测试

根据图1 所示的系统拓扑结构，参照目前已投入运行的昆柳龙三端混合高压直流输电工程参数，在PSCAD/EMTDC 中搭建三端混合高压直流输电系统模型进行仿真测试。系统采用双极接线方式，换流站均接地。直流线路采用频变参数模型，其中，直流线路L1长932 km，直流线路L2长557 km。模型参数如附录A 表A1 所示。

在MATLAB 中编写相关程序，并导入所建PSCAD/EMTDC 模型的故障仿真数据，验证保护的动作情况。设置测点的采样频率为5 kHz，数据窗取10 ms。

4.1 故障保护判据性能测试

由于正负极线路具有对称性，故以线路L1的正极保护为例进行说明。设置不同故障类型、不同位置、不同过渡电阻的区内外故障，过渡电阻Rf最大取600 Ω，故选择8 Hz 的低通截止频率。差动电流与分布电容电流的仿真波形如附录A 图A1 至图A3所示，保护的整定值如附录A 表A2 所示，仿真结果如附录A 表A3 所示。由表A2、A3 可以看出，在单极故障和极间故障下，保护均能正确识别出区内故障，保护装置可靠动作；而在任何类型的区外故障下，故障保护判据均不满足，保护装置可靠不动作。并且，本文所提保护具有较强的耐过渡电阻能力，即使是在600 Ω 的区内高阻故障下，保护依然能够正确可靠动作，过渡电阻对保护的灵敏性并没有太大的影响。

4.2 数据窗时长对保护的影响

对差动电流和分布电容电流进行平均值计算时，选择的数据窗长度不同，计算得到的效果也会不同。以线路L1的正极保护为例，验证数据窗长度对保护动作的影响。分别设置线路区内故障、对极故障以及区外故障，数据窗分别取6、10、16 ms，所提判据的仿真结果如表1 所示。

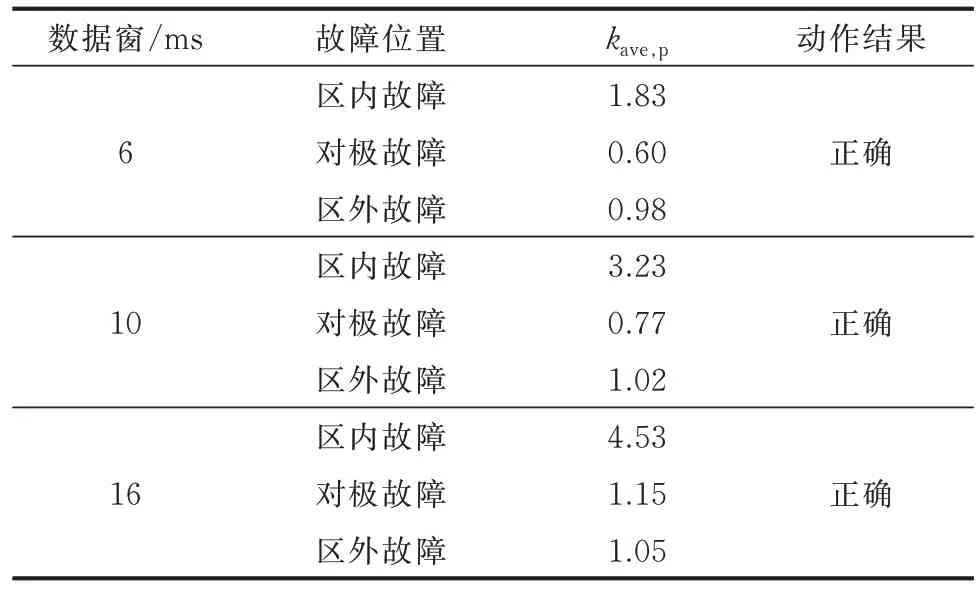
表1 不同数据窗时长下保护动作结果Table 1 Protection operation results for different data window durations

由表1 可以看出，在6、10、16 ms 的数据窗长度下保护均能正确动作。只是在6 ms 的数据窗下，区内故障下的kave，p数值将变小，这是不利于区内故障的识别的；而数据窗越长，区内故障下的kave，p值就越大，越有利于区内故障的判别。

图4 给出了差动电流绝对值|id|和分布电容电流绝对值|ic|在区内故障下的故障电流波形仿真图（过渡电阻为600 Ω）。从图中可以看出，在线路区内故障的初始阶段，分布电容电流和差动电流同时上升，但是分布电容电流的数值较小且上升速度较快，在数毫秒内就能达到峰值；而差动电流则上升相对缓慢且持续上升到一更高的数值。

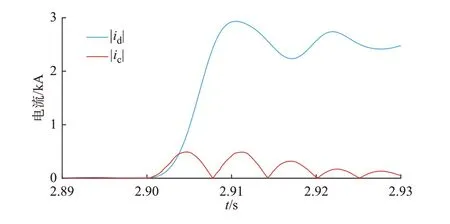
图4 |id|和|ic|在区内故障下的仿真波形图Fig.4 Simulation waveform diagram of |id| and |ic|under internal fault

因此，当数据窗长度较小时，提取到的故障特征是差动电流和分布电容电流同时上升，此时，区内故障下所对应的kave，p数值将减小；而数据窗较长时，差动电流相较于分布电容电流已经有了明显上升，此时，区内故障下所对应的kave，p数值较大，且数据窗越长，kave，p值就越大，越有利于故障的识别。但是，较长的数据窗必然会影响保护的整体动作时间。因此，本文综合考虑保护的可靠性和速动性后，最终选择10 ms 的数据窗时长。

4.3 同步误差对保护的影响

本文所提保护利用差动电流与线路分布电容电流的比值识别区内外故障。在提取故障特征的时候，先计算一段时间窗内的差动电流与线路分布电容电流之和，再对二者进行均值计算。由于保护利用的是一段时间窗内的数据，故可靠性较高，可以承受一定数据不同步的影响。

为了验证同步性对本文所提保护的影响，考虑0、1、2 ms 同步误差的情况，所提判据的仿真结果如表2 所示。

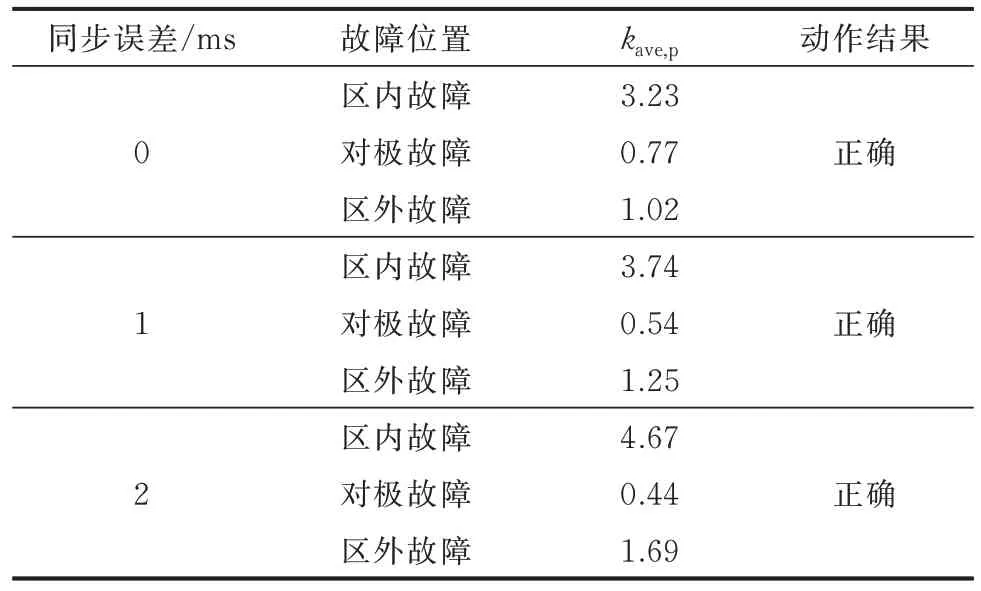
表2 不同同步误差下保护动作结果Table 2 Protection operation results with different synchronization errors

由表2 可以看出，即使是在2 ms 的同步误差下，保护仍然可以正确动作，数据不同步虽然会使保护判据具体计算的特征量大小略有不同，但是所提判据仍然能够保证保护的选择性和可靠性。

4.4 噪声干扰对保护的影响

大部分的行波保护和纵联方向保护抗噪声干扰能力都较弱，容易受到噪声干扰的影响，造成保护误动。给本文所提保护分别加上信噪比为50、40、30 dB 的高斯白噪声干扰，所提保护的仿真动作结果如表3 所示。

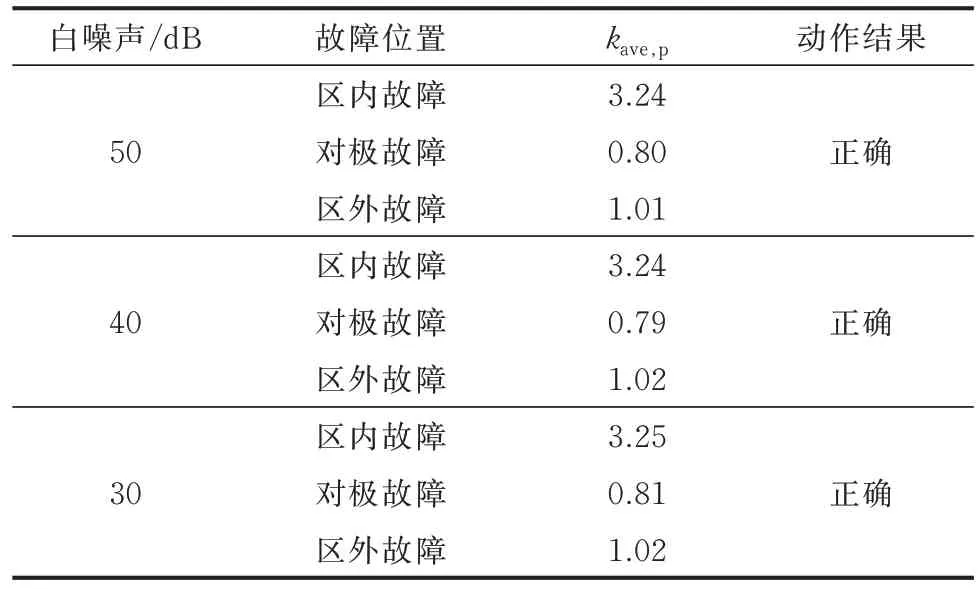
表3 不同白噪声下保护动作结果Table 3 Protection operation results under different white noises

由表3 可以看出，即使加入30 dB 的白噪声干扰，保护依然能够正确动作，本文所提保护具有较高的抗噪声干扰能力。

4.5 采样频率对保护的影响

考虑到本文所提方法利用的是经过低通滤波后的故障低频特征，故对采样频率没有太高的要求。而在性能相同的情况下，采样频率更低可以减少保护的运算量，故本文采用5 kHz 的采样频率。表4 给出了所提保护在5 kHz、10 kHz 采样频率下的仿真结果。由表4 可以看出，在5 kHz 和10 kHz 的采样频率下，所提保护均能正确识别故障，两者没有明显差别，几乎不受采样频率影响。

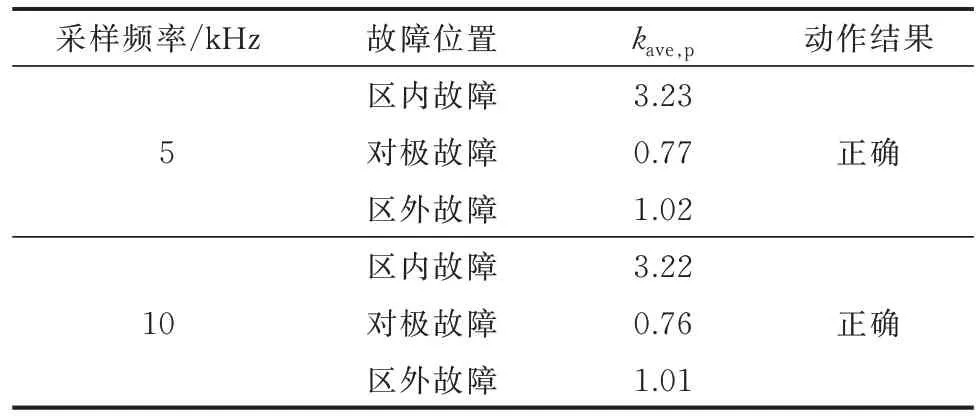
表4 不同采样频率下保护动作结果Table 4 Protection operation results under different sampling frequencies

4.6 线路长度、边界条件对保护的影响

为了验证所提保护对不同长度、不同边界条件的直流线路均适用，对直流线路L2进行仿真测试。直流线路L2长557 km，线路单位长度电容C0取1.31×10-11F/m，过渡电阻Rf取600 Ω，kv取0.9，根据式（21）可得截止频率fc＜16.37 Hz，向下取整后取截止频率fc=16 Hz。线路保护的仿真结果如附录A表A4 所示。从表A4 可以看出，本文所提保护在不同的线路长度、边界条件下均能正确动作，且在更短的线路中效果更好。

4.7 与改进电流差动保护的对比

文献［20］研究了线路分布电容电流的估算方法并提出了一种基于分布电容电流补偿的电流差动保护方案。

4.7.1 灵敏性的对比

文献［20］本质上是对分布电容电流进行补偿后，利用差动电流的大小识别区内外故障。图5、图6 分别为文献［20］所提方法在区内金属性故障和区内600 Ω 过渡电阻故障下的仿真结果。从图中可以看出，在区内金属性故障下，差动电流的最大值超过了20 kA，远大于最小动作电流；而在区内高阻故障下，差动电流的最大值不足1.5 kA，保护的灵敏性裕度已大大降低了。

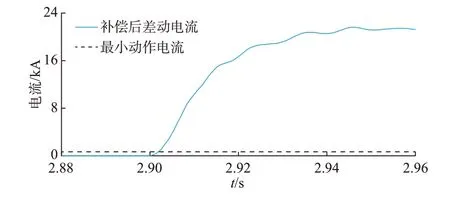
图5 区内金属性故障的仿真结果Fig.5 Simulation results of internal metallic faults

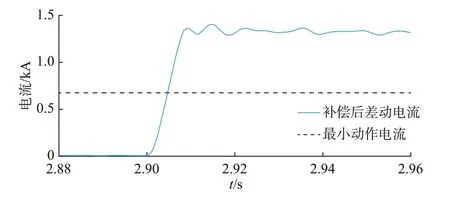
图6 区内高阻故障的仿真结果Fig.6 Simulation results of internal high-resistance faults

而本文所提保护方案采用差动电流与分布电容电流的比值作为判据，可以削弱过渡电阻对判据的影响，提高保护的灵敏性。

4.7.2 数据同步误差的对比

图7 为整流侧发生区外故障时，对差动电流进行补偿后的仿真结果。

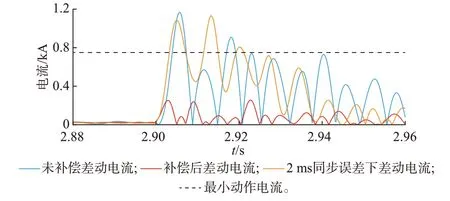
图7 整流侧区外故障下的仿真结果Fig.7 Simulation results of external fault at rectifier side

由图7 可见，补偿前，由于分布电容电流的影响，差动电流在故障发生的起始阶段会超过最小动作电流；而经过补偿后，上述情况可以得到有效的改善；而在一定的同步误差（2 ms）情况下，区外故障的差动电流中仍然会出现较大的不平衡电流，从而对保护的动作性能造成一定的影响。因此，文献［20］提出的改进电流差动保护仍然对双端数据的同步有较高的要求。