基于多能量场景谐振域构建的风机控制器参数优化方案

丁 炅，朱介北，陈彬彬，李云丰，王 伟，俞露杰，贾宏杰

（1.智能电网教育部重点实验室（天津大学），天津市 300072；2.广西电网有限责任公司，广西壮族自治区南宁市 530032；3.长沙理工大学电气与信息工程学院，湖南省长沙市 410004；4.南瑞集团有限公司（国网电力科学研究院有限公司），江苏省南京市 211106）

0 引言

风机通过电力电子换流器接入交流电网，而换流器与交流电网间的动态交互作用可能导致电网抗扰动能力降低、威胁电网的安全稳定运行，进而制约风能的大规模开发与利用［1-4］。近年来，全球范围内已出现多起由二者动态交互所引发的宽频振荡事故。例如，2015 年新疆哈密地区直驱风电场与弱交流系统交互引发了火电机组扭振跳闸［5］；2009 年美国得克萨斯州双馈机组与串补装置交互引发的次同步振荡［6］。文献［7-8］指出，互联系统中换流器与同步机之间的交互作用更容易引发系统的低频振荡。

不同能量场景（例如同步机在线数量与出力变化）下新能源并网系统呈现不同的特性，故考虑能量场景变化对新能源并网系统的动态交互分析与稳定性评估至关重要［8-10］。基于多场景稳态模型，文献［11］分析了场景变化对风电场一次调频能力的影响，但未关注系统在扰动恢复过程中的振荡稳定。文献［12］评估了在不同场景下电力系统的运行风险，但该评估局限于系统的功率平衡与潮流收敛，不涉及系统在多场景下的小干扰稳定。

为了研究风机并网系统在小扰动后的振荡特性，文献［13］搭建了详细的小信号稳定模型（smallsignal stability model，SSSM）。 文 献［14］基 于SSSM 进行参与因子分析，研究了风机并网引入的振荡模式。但文献［13-14］均未计及风机与交流系统状态变量的动态交互对系统稳定性的影响。文献［15］采用阻尼转矩分析（damping torque analysis，DTA）方法研究风机动态特性对同步发电机阻尼转矩的贡献，用于解释风机与交流系统间的动态交互机理，但未指出风机和交流系统间产生强动态交互的判定条件。

文献［16-21］采用开环模式谐振的方法研究风机并网系统中子系统之间的动态交互作用。文献［16-17］将永磁同步发电机（PMSG）并网系统划分为两个开环子系统，分别为风机子系统和多机交流子系统，定义由开环模式在复平面上相互靠近引起的闭环模式排斥作用为开环模式谐振。开环模式谐振方法可以基于子系统的开环模型，从谐振的角度判定子系统间强动态交互的触发条件，进而分析闭环系统的稳定性。然而，文献［16-17］仅提出了模式谐振的概念，没有涉及系统能量场景的变化对模式谐振的影响。文献［18-19］采用模式谐振方法研究了PMSG 控制回路与多机交流子系统间的动态交互，发现锁相环（PLL）的相位跟踪误差是引发谐振的主要原因之一，但未涉及模式谐振的强度评估及抑制方案。文献［20］分析了由谐振引入的模式偏移量对PMSG 控制参数的灵敏度，评估控制参数对子系统间谐振强度的影响，但同样忽略了能量场景变化对偏移量和灵敏度的影响。为应对多种不同能量场景，文献［21］提出了一种基于广域测量系统的在线模式谐振分析方案。然而，在线分析不仅依赖于电网中同步相量测量装置的广泛部署，而且要处理大量实时数据，同时可能不必要地重复分析相似的能量场景，进一步增加计算负担。

为了评估谐振对系统振荡特性的影响，文献［20-24］分别定义了不同的衡量指标。文献［22］提出了旨在估计模式闭环位置的相互作用指标，但该指标没有涉及谐振对系统振荡阻尼影响的量化。文献［23-24］提出了可判断闭环系统在发生谐振后是否失稳的模式谐振指标，但对谐振强度的衡量不够精确。文献［20-21］定义的激励指标为发生谐振的两个模式的闭环距离与相应的开环距离之比，以衡量谐振模式间排斥作用的强度，但该指标无法体现排斥作用对模式振荡阻尼变化的影响，而该变化是分析谐振对系统小干扰稳定影响的关键。

为了降低谐振对系统稳定性的负面影响，通常采用参数优化的方式避免触发两个或多个开环模式谐振的产生条件。文献［25］提出了一种基于参数域的控制器参数优化方案，但该方案仅关注换流器自身的稳定性，没有涉及子系统间的谐振稳定性。文献［26］基于分岔理论给出了构建确保系统稳定的同步机有功出力功率域，但该方案的功率域可能会导致同步机出力的不连续调节。文献［27］从避免模式谐振的角度设计了控制器参数的安全域，但此参数域仅针对特定系统运行状态有效，忽略了电力系统的时变特性；此外，当控制器参数较多时，参数空间维度较高，给安全域边界的确定带来困难。文献［20］通过参数优化削弱了两个子系统之间的模式谐振强度，但该方案在优化过程中没有涉及系统能量场景的变化，导致优化后的参数仅适用于系统某一特定能量场景。而在实际的风机并网系统中，某一场景下的最优参数可能会在其他场景下激发出新的模式谐振。基于振荡模式识别结果，文献［21］提出了一种在线谐振抑制方案，但该方案在采集、处理和运算实时数据过程中均可能引入时间延迟，无法及时削减谐振，也无法应用于日前优化。

为避免在多种可能能量场景下风机子系统与多机交流子系统间潜在的模式谐振，本文提出了一种基于谐振域（resonance area，RA）的控制器参数优化（下文简称RAC）方案，主要特点如下:

1）不同于文献［16-20］，本文所提RAC 方案在谐振分析过程中引入了系统能量场景的变化；

2）不同于文献［16-21］，RAC 方案中的RA 能够捕捉在多能量场景下发生模式谐振的可能区域；

3）不同于文献［20-24］，RAC 方案中的谐振强度指标（resonance strength index，RSI）能够准确衡量谐振的强度及其对模式振荡阻尼的影响；

4）RAC 方案基于RA 和RSI，对风机控制器参数进行优化，能够有效削弱多能量场景下其与多机交流子系统的模式谐振强度。

1 系统建模与模式谐振分析

为研究电网各子系统之间的动态交互，可在风机公共耦合点（PCC）将闭环系统划分为两个开环子系统，即PMSG 子系统和多机交流子系统，如图1所示。PMSG 子系统由风机、机侧换流器（MSC）、网侧换流器（GSC）、直流链路、滤波器、变压器以及MSC 和GSC 的控制系统组成。在GSC 控制系统中，采用PLL 使PMSG 与电网实现动态同步。由文献［16-20］可知，由于MSC 和GSC 之间的动态解耦，PMSG 和多机交流子系统之间的动态相互作用由GSC 的状态变量主导。

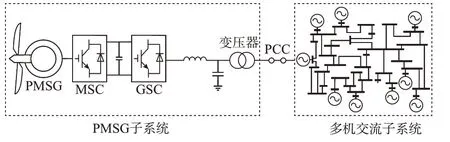
图1 PMSG 并网系统模型Fig.1 Grid-connected system model of PMSG

1.1 开环子系统和闭环系统的SSSM

以PCC 处的电压变化量ΔVpcc为输入、电流变化量ΔIpcc为输出，则GSC 的SSSM 可表示为［16］:

式中:ΔXG为由GSC 状态变量组成的列向量；AG、BG、CG、DG为系数矩阵。

GSC 的传递函数H（s）可以表示为:

式中:I为单位矩阵。

对于多机交流子系统，若以ΔIpcc为输入、ΔVpcc为输出，则其SSSM 可以表示为［28］:

式中:ΔXm为多机交流子系统状态变量组成的列向量；Am、Bm、Cm、Dm为系数矩阵。

类似地，其传递函数G（s）可以表示为:

计算式（1）和式（3）的状态矩阵特征值可分别得到开环状态下GSC 振荡模式（GSC oscillation mode，GOM）和多机交流子系统的机电振荡模式（electromechanical oscillation mode，EOM）。根据模式的参与因子，可以进一步得到状态变量和控制参数在GOMs 或EOMs 中的参与度［13］。

为了对比开环和闭环状态下系统振荡模式的差异，建立闭环系统的SSSM 如下［21］:

闭环系统的传递函数模型如图2 所示。图中:Ipcc0为稳态时风机子系统注入交流子系统的电流初始值；Ipcc为受风机子系统动态特性影响后，电流注入的实际值；Vpcc0为稳态时PCC 处电压值；Vpcc为受风机动态特性影响的PCC 处电压实际值。在分析子系统间动态交互时，可以将GSC 子系统视为以ΔVpcc为输入、ΔIpcc为输出的多机交流子系统扰动反馈回路。由式（5）的状态矩阵可计算出闭环系统的振荡模式，而闭环振荡模式与开环振荡模式在复平面上的位置偏差代表两个子系统间动态交互作用引入的系统小干扰稳定性变化。

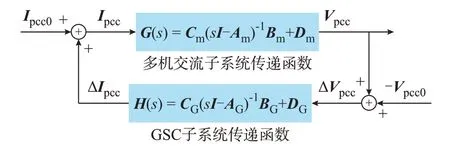
图2 闭环系统传递函数模型Fig.2 Transfer function model of closed-loop system

1.2 模式谐振机理分析

模式谐振是一种导致闭环系统小干扰稳定性降低的GSC 子系统与多机交流子系统间的强动态交互作用［16-19］。GSC 对多机子系统稳定性的影响可以通过风机接入前后（从开环状态到闭环状态）EOM的模式偏移量来衡量，模式偏移量Δλei可表示为［20］:

式中:λei为多机交流子系统的第i个EOM；Sik为λei对同步机k的阻尼转矩灵敏度；n为同步机台数；F(·)为ΔIpcc到阻尼转矩的前向传递函数；γ(·)为ΔVpcc到同步机角速度的传递函数。传递函数的推导过程详见文献［20］。

若Δλei较小，则说明GSC 与多机交流子系统间的动态交互作用较弱，系统稳定性不会受到显著影响。然而，当两个子系统的振荡模式满足谐振触发条件时，即开环GOM 和EOM 在复平面上相互靠近时，由谐振引入的强动态交互作用会导致较大的模式偏移。为了进一步解释这一现象，式（2）的传递函数H（s）可改写为留数形式，即

式中:λgj为GSC 子系统的第j个GOM；RGSC和DGSC为H（s）的留数向量；J为GOM 的数量。由（7）可知，当λgj与λei在复平面上相互靠近（λgj≈λei）时，分母趋近于0，使得式（6）中的H(λei)的增益变大。此时，GSC 的动态特性使多机交流子系统的EOM 产生显著的模式偏移。

由多机交流子系统的动态特性引起GOM 的模式偏移量Δλgj也可以通过式（6）和式（7）的方法近似估计。通过式（6）和式（7），可以利用开环子系统的SSSM 来判断闭环系统的小干扰稳定性。由于每个子系统的状态变量数目远小于闭环系统的状态变量数目，基于模式谐振小干扰稳定性分析方法在一定程度上避免了传统分析方法的“维数灾”问题［17］。

然而，上述模式谐振分析不涉及子系统能量场景的变化，而在不同能量场景（例如，同步机在线数量的变化及其有功和无功输出的波动）下，子系统的开环模式会呈现不同的振荡特性，EOM 和GOM 的数量和在复平面上的分布位置也会随场景的变化而变化，导致谐振分析结果仅在单一场景下适用。同时，基于单一场景优化的GSC 控制参数无法有效抑制多场景下的模式谐振，甚至可能在能量场景变化时激发新的模式谐振（该变化现象可在3.2 节的仿真结果中观测到）。为了解决上述问题，本文提出了RA 的概念以及基于RA 的风机控制器参数优化方案，旨在削弱子系统在多能量场景下的模式谐振强度。

2 基于RA 的控制器参数优化方案

为削弱多能量场景下EOM 和GOM 的模式谐振强度，本章提出了RAC 方案。首先，在所建的SSSM 中反映子系统能量场景的变化；其次，用数学方式表示在可能的多能量场景下EOM 和GOM 在复平面上的所有位置，并捕捉发生模式谐振风险较大的区域，即RA；设计衡量谐振强度以及谐振对模式振荡阻尼影响的RSI；最后，基于RA 和RSI 优化风机控制器参数，削弱其在多能量场景下与多机交流子系统的模式谐振强度。

2.1 计及能量场景变化的SSSM

为了引入能量场景变化对开环子系统振荡模式的影响，本文对式（3）的SSSM 进行等效变换，如附录A 式（A1）—式（A10）所示。因此，计及能量场景变化影响的开环EOM 的特征值λEOM可以表示为:

式中:Z=［z1，z2，…，zk，…，zn］T为同步机的状态向量，zk=1 表示同步机k在线运行，zk=0 表示退出运行；P=［P1，P2，…，Pk，…，Pn］T和Q=［Q1，Q2，…，Qk，…，Qn］T分别为同步机的有功和无功输出向量；eig(·)表示求解矩阵的特征值。

在系统能量场景变化过程中，每台同步机满足如下运行约束条件:

式中:Pload和Qload分别为系统包含网损在内的有功和无功需求之和；Pk和Qk分别为同步机k的有功和无功输出；φk为同步机k的功率因数角；下标min 和max 分别代表变量的最小值和最大值。式（9）的约束条件来自特定的同步机并网导则［29］。

式（8）中的变量包含了影响多机交流子系统开环振荡模式的关键因素，即同步机的运行状态、同步机的有功和无功出力变化。如果需要研究网络结构等其他因素的影响，可以通过修改附录A 式（A7）中的节点导纳矩阵，将线路的开断情况反映在子系统的开环SSSM 和EOM 中。

2.2 EOM 和GOM 的位置区域

由式（6）和式（7）的模式谐振原理可知，谐振的触发条件取决于子系统开环模式在复平面上的位置关系，与模式的振荡频率无关。为了减少额外的计算量，可以根据实际应用需要设定所关注的频段和阻尼比范围，筛选出此频率和阻尼比范围内有谐振风险的所有振荡模式。本文主要针对由低频和低阻尼比模式引发的模式谐振，故设定所研究的频率和阻尼比范围为:

式中:fB为频率范围（本文选取［fmin，fmax］=［0.1，2.5］Hz）；ζB为 阻 尼 比 范 围（本 文 选 取［ζmin，ζmax］=［0.01，0.20］）。

由式（8）可知，随着系统能量场景的变化，开环EOM 在复平面上的位置会相应改变，而这种改变可能导致第1 章的谐振分析不准确。为了实现多能量场景下的谐振分析，本节采用一种特征值区域定界方法来捕捉在可能的能量场景变化下EOM 在复平面上的所有位置。对于特定的同步机在线数量，当同步机输出有功和无功功率在式（9）的约束范围内变化时，包含同一个EOM 所有可能位置的区域定义 为EOM 特 征 值 区 域（EOM eigenvalue area，EEA），其确定流程如下。

将系统初始状态设为S0=[P0，Q0]（P0和Q0分别为有功和无功功率的初始状态），该状态下谐振相关EOM 可由式（8）和式（10）得到，记为Λ0。从S0开始，后续的状态可以表示为:

式中:Sl为第l次搜索的系统状态；ΔSl为从［Pmin，Qmin］到［Pmax，Qmax］的第l次搜索步长。对于每次搜索，根据式(8)更新多机交流子系统的振荡模式，得到第l次搜索的EOM，记为Λl。

经过m次搜索，同一EOM 的m个离散位置在复平面上构成一个EEA，如图3 所示。

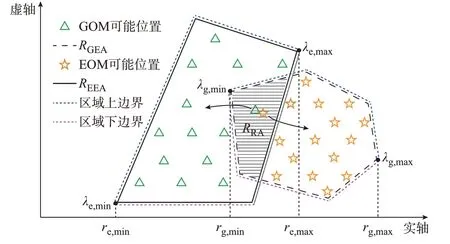
图3 EOM 与GOM 特征值区域以及RA 的构建Fig.3 Construction of eigenvalue regions and RA for EOM and GOM

为了用数学方式表示EEA，首先，采用Graham算法［30］从m个离散的特征值中选取出位于EEA 边界上的特征值，并将其分为上特征值边界和下特征值边界两部分:

式中:λm为EOM 的特征值边界；λe，min和λe，max分别为实部最小和最大的特征值；λU和λL分别为上、下边界特征值组成的向量。

其次，采用拉格朗日插值函数［31］来拟合离散的上下特征值边界:

式中:feL（r）和feU（r）分别为EEA 的下边界和上边界函数，其中r为振荡模式的实部；nL和nU分别为下边界和上边界特征值的数量；rL，a和Le(rL，a)分别为第a个下边界特征值的实部和虚部；rU，c和Ue(rU，c)分别为第c个上边界特征值的实部和虚部；re，min和re，max分别为λe，min和λe，max的实部。

EEA 可以表示为:

值得注意的是，由式（14）得到的EEA 包含了一个EOM 在可能变化的能量场景满足运行约束下的所有位置。与文献［16-20］仅使用单一能量场景的谐振分析相比，本文得到的EEA 更适用于研究可能的能量场景变化下子系统间的模式谐振，可更加全面地分析系统的谐振稳定性，也避免了在不同能量场景下对系统的反复建模。

对于满足式（10）的GOM，通过参与因子识别出与其相关的状态变量和控制参数，实际系统中控制器参数可以在一定范围内调节，故定义参数的变化范围pg为:

式中:p0为参数初始值向量，包含与GOM 相关的所有参数；α为调节系数，用来确定参数变化范围（本文取α=2/3）。

类似地，基于式（1）的GSC 模型与式（15）的参数变化范围，GOM 特征值区域（GOM eigenvalue area，GEA）可以表示为:

式中:fgL（r）和fgU（r）分别为GEA 的下边界函数和上边界函数；rg，min和rg，max分别为GEA 实部的最小和最大值。

文献［32-34］证实，风速变化对系统小信号稳定性的影响远小于控制参数变化的影响。因此，本文在构建GEA 的过程中，主要研究风机子系统控制参数的变化。

2.3 RA 的定义与数学表达式

如图3 所示，复平面上，EEA 与GEA 的重叠区域定义为RA，如果在能量场景变化的过程中开环EOM 和GOM 相互靠近并引发模式谐振，则EOM和GOM 一定同时位于此RA 内。根据图3 中RA 边界与EEA 和GEA 上下边界的关系，RA 可表示为:

式中:fL（r）和fU（r）分别为RA 的下边界函数和上边界函数；rmin和rmax分别为RA 实部的最小和最大值。

基于式（6）和式（7）的模式谐振条件与式（17）的RA 定义，为了避免多能量场景下开环GOM 与EOM 在复平面上相互靠近，可以对GSC 参数进行优化，使GOM 位于有谐振风险的RA 之外。

2.4 RSI

为了衡量谐振的强度及谐振对模式振荡阻尼的影响，本文设计了RSI，用于指导控制器参数优化。

式中:λci和λi分别为闭环和开环状态下的第i个振荡模式；Δλi为第i个振荡模式偏移量。

RSI 代表着发生谐振后闭环振荡模式相对于其开环位置的水平偏移程度。RSI 有3 种可能的状态:

1）IRSI＜0(Δλi＜0):在左半复平面上，谐振使闭环模式远离虚轴，模式振荡阻尼增加；

2）IRSI≈0(Δλi≈0):模式偏移量约为0，谐振对该模式的振荡阻尼几乎没有影响；

3）IRSI＞0(Δλi＞0):在左半复平面上，谐振使闭环模式靠近虚轴甚至越过虚轴位于右半平面，模式振荡阻尼降低甚至系统失稳。

本文重点关注谐振对系统稳定性的负面影响，故进一步说明状态3）的含义。0 ＜IRSI＜C1定义为可忽略的“弱”模式谐振，本文取C1=0.2，代表模式的水平偏移程度小于20%；IRSI＞C2定义为显著的“强”模式谐振，本文取C2=0.8，代表模式的水平偏移程度大于80%；IRSI＞C3定义为需要严格避免的“失稳”模式谐振，本文取C3=1，代表偏移量大于开环模式与虚轴的距离，即闭环模式位于右半复平面，系统失稳。RSI 可以衡量模式谐振强度及对振荡阻尼的影响，并指导GSC 控制参数的优化。

2.5 基于RA 和RSI 的控制器参数优化

对于大型复杂多机交流系统，通过改变其参数使EOM 位于RA 外的挑战较大（EOM 微小的位置变化可能需要改变多个或多组同步机控制器参数）［28］。相比之下，GSC 控制参数与GOM 位置的关系相对简单。因此，本文设计了一种基于RA 和RSI 的GSC控制器参数优化方案，旨在削弱系统在多能量场景下的模式谐振强度。

本文的优化方案将具有谐振风险（位于RA 内）的GOM 优化到RA 之外，并最小化RSI，从而降低谐振对振荡阻尼的负面影响，其优化函数表示为:

式中:F(·)为目标函数；pg为待优化的GSC 控制器参数；pg，min和pg，max分别为GSC 参数范围的最小值和最大值；RGEA/{RRA1⋃RRA2⋃…⋃RRAn}表示除去n个RA 的GEA。求解式（19），获得RSI 最小值与GSC最优控制参数。

RAC 方案的流程如图4 所示，具体如下:1）在式（10）的频率和阻尼比范围内确定待研究的EOM和GOM；2）通过参与因子得到与GOM 相关的控制器参数；3）通过式（11）—式（17）得到由EOM 和GOM 引入的RA；4）计算RSI，衡量模式谐振的强度；5）当检测到开环GOM 落入RA 时，优化GSC 控制器参数，通过求解式（19）确保GOM 位于RA 之外且使RSI 最小，得到最优GSC 控制器参数。

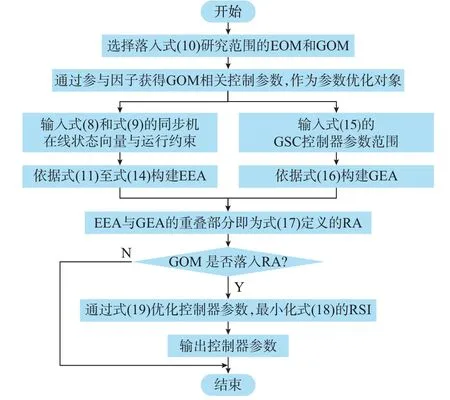
图4 RAC 方案的流程图Fig.4 Flow chart of RAC scheme

对于不同新能源子系统（例如双馈机组、光伏电站），RAC 方案本质上是基于子系统开环模型的谐振分析与抑制策略，其谐振触发条件取决于两个子系统开环振荡模式的位置关系，与子系统的电路结构与控制方式无关。因此，RAC 方案同样适用于其他新能源场站或其他控制方式下的风电场与交流系统之间的谐振分析。当系统中存在多个新能源场站且位于不同地理位置时，可以分别建立每个场站的子系统开环模型，并逐一采用RAC 方案进行谐振分析与参数优化。当子系统规模较大时，可以将子系统进一步细分为若干更小一级的子系统，建立其开环模型，构建RA，从而研究子系统内部的模式谐振。

3 案例分析

为了验证RAC 方案在多能量场景下通过构建RA、衡量模式谐振强度来优化GSC 控制器参数的有效性，本文基于DIgSILENT/PowerFactory 平台搭建了如图5 所示的IEEE 39 节点标准模型［35］，并将含PMSG 的风电场通过母线2 接入39 节点系统，风机关键参数见附录B 表B1。设置同步机的在线数量分别为4 台、7 台和10 台，以模拟典型电力负荷谷时、平时和峰时的能量场景。

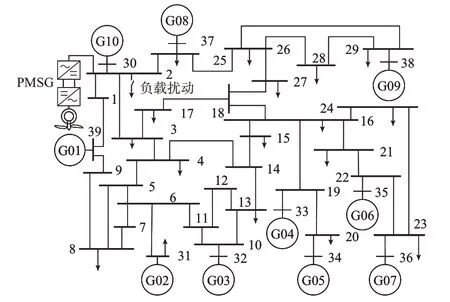
图5 PMSG 接入IEEE 39 节点系统的模型Fig.5 Model of IEEE 39-bus system integrated with PMSG

依据典型的同步机运行约束条件［28-29］，设置式（9）中同步机有功功率变化范围为0.4～1.0 p.u.，功率因数变化范围为滞后0.85 至超前0.95。根据式（8）计算不同场景下EOM，进一步判定在式（10）频率和阻尼比范围内的EOM 为本文研究的关键振荡模式。

如附录B 表B2 所示，风机子系统的振荡模式GOM1 的振荡频率和阻尼比在式（10）设定的频率和阻尼比范围内，而GOM1 主要与GSC 的PLL 控制参数相关。因此，本文的案例分析将优化风机PLL 参数。GSC 的PLL 比例-积分（PI）参数的初始值分别为Kp=1.5、Ki=120，则依据式（15）设定PLL参 数 的 变 化 范 围 为0.5≤Kp≤2.5、80≤Ki≤60，由GOM1 通过式（16）构建的开环特征值区域为RGEA1。

3.1 负荷谷时能量场景：4 台同步机在线

在谷时能量场景中，图5 中在线运行的4 台同步机分别为G01、G02、G07 和G09。如附录B 表B2 所示，机电振荡模式EOM1 的振荡频率为1.47 Hz，阻尼比为0.081，是本场景下的关键振荡模式。在同步机的出力运行约束下，依据式（11）—式（14）在复平面上构建包含EOM1 所有可能位置的REEA1，如图6中的虚线框所示。

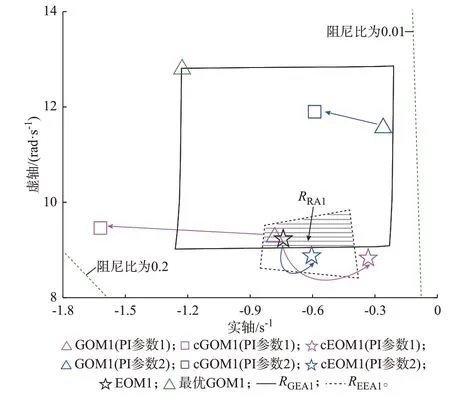
图6 谷时场景下的RGEA1、REEA1、RRA1，以及不同参数下GOM1 与EOM1 的 模 式 偏 移Fig.6 RGEA1， REEA1， RRA1 and modal shifts of GOM1 and EOM1 with different parameters in valley-period scenario

由式（11）和式（12）分别得到如附录B 表B3 所示的EOM1 和GOM1 特征值边界，根据式（13）分别建立EOM1 和GOM1 的上、下边界函数，然后根据式（14）和式（16）分别建立EEA1 和GEA1 的数学表达式。最后，通过式（17）可得REEA1与RGEA1的重叠区域，即谐振域RRA1:

在PLL 参数变化范围内，随机取PI 参数Kp=1.56、Ki=84，GOM1、闭 环 GOM1（closed-loop GOM1，cGOM1）、闭环EOM1（closed-loop EOM1，cEOM1）以及由式（18）计算得到的GOM1 和EOM1的RSI 如表1 所示。通过观察 图6 可知，GOM1 位于RRA1内部，意味着GOM1 与G07 主导 的EOM1 有发生模式谐振的风险。而IRSI(EOM1)为0.453 证实了模式间存在一定强度的谐振作用，闭环系统cEOM1从-0.75+9.23j 被 排 斥 到-0.41+8.92j，阻 尼 比从0.081 减小到0.046，系统的小干扰稳定性降低。图7 的时域仿真结果进一步验证了这一点，在母线2增加10 MW 的负荷阶跃后，含PMSG 的风电场PCC 处测得的系统频率与G07 输出功率均出现了明显振荡，其振荡频率约为1.42 Hz，幅值收敛较缓慢。

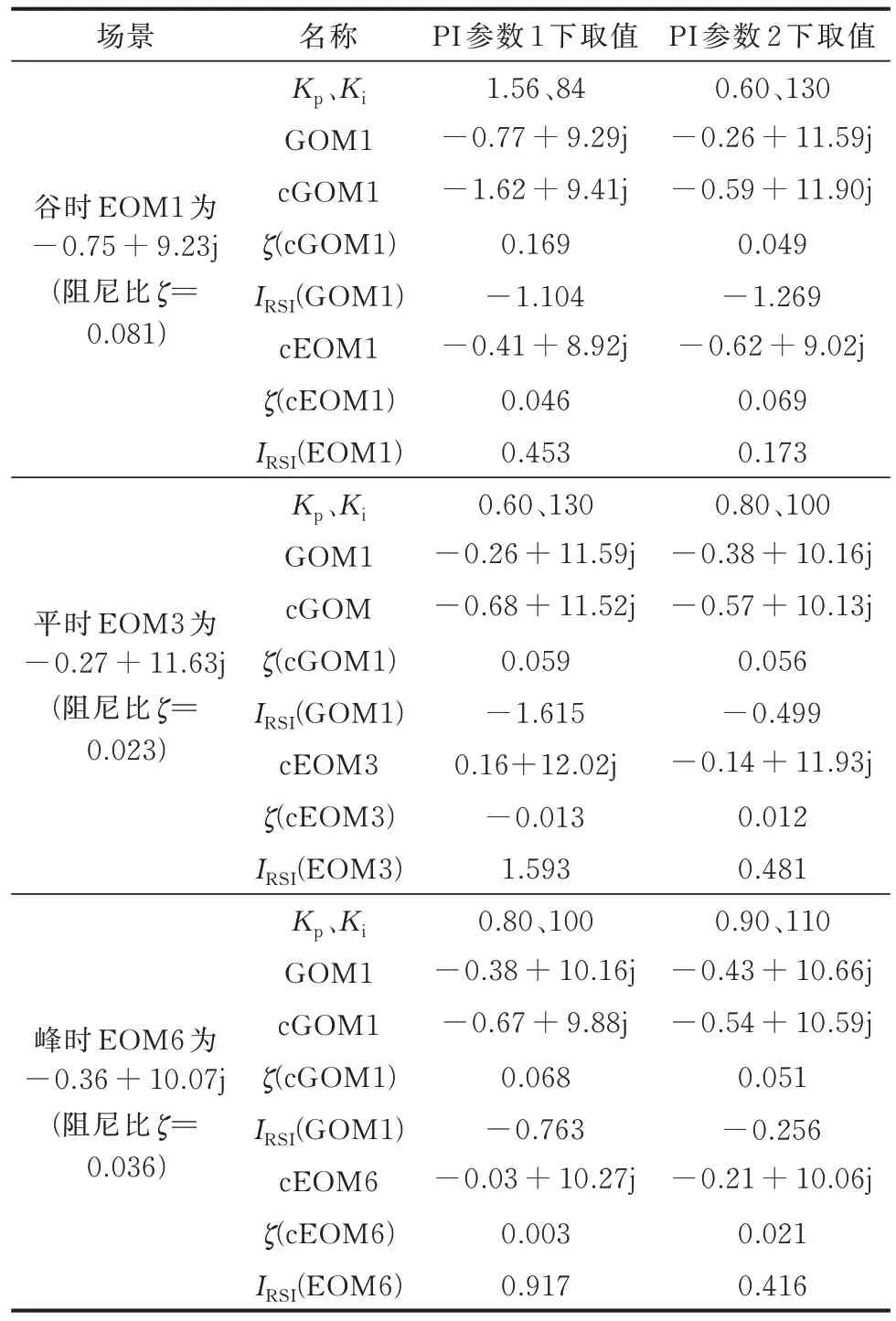
表1 不同场景下和GOM1 位置下的模式偏移和RSITable 1 Modal shift and RSI in different scenarios and GOM1 positions

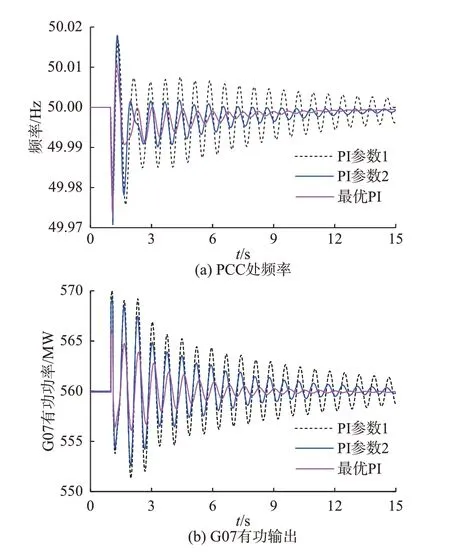
图7 谷时场景不同PI 参数下的时域仿真Fig.7 Time-domain simulation with different PI parameters in valley-period scenario

当PLL 采取另一组变化范围内的随机PI 参数Kp=0.60、Ki=130 时，此 时GOM1 位 于RRA1之 外，如图6 所示，意味着子系统之间不会产生很强的模式谐振。根据表1 可知，IRSI(EOM1)为0.173，同样表明系统的模式谐振较弱，图7 所示时域仿真结果也验证了这一点。

本文所提RAC 方案通过式（19）对PLL 参数进行优化，得到最优参数Kp=2.5、Ki=160，在该参数下相应的IRSI(EOM1)为0.067，如图8 所示。优化后的GOM1 在复平面上的位置如图8 中红色点所示。最优参数下的cGOM1、cEOM1、IRSI(GOM1)在表2中给出。如图7 的时域仿真结果所示，在同样的扰动下，与其他两组非最优参数相比，RAC 方案有效降低了系统的模式谐振强度。

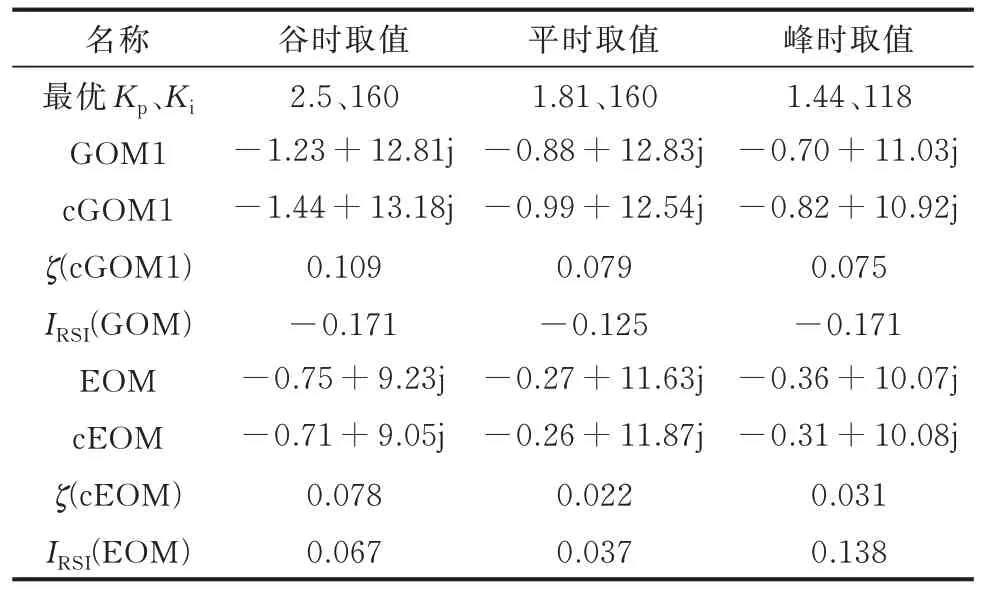
表2 不同场景下的最优参数以及RSITable 2 Optimal parameters and RSI in different scenarios

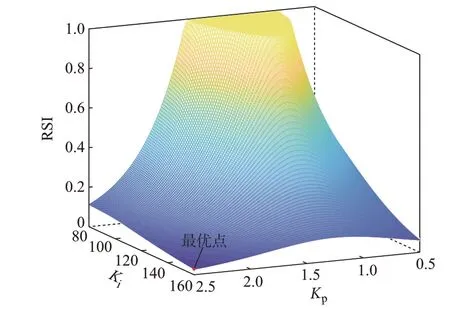
图8 谷时场景下用于参数优化的RSIFig.8 RSI for parameter optimization in valley-time scenario

3.2 负荷平时能量场景：7 台同步机在线

在平时能量场景中，图5 中在线运行的7 台同步机分别为G01、G02、G04、G06、G07、G09 和G10，同步机的出力运行约束与谷时能量场景相同。平时能量场景中两个关键振荡模式分别为EOM2 和EOM3，如附录B 表B2 所示。与负荷谷时能量场景的分析类似，在同步机的出力运行约束下，EOM2 和EOM3 在复平面上的所有可能位置形成了如附录B图B1 所示的REEA2和REEA3。根据表B3 的特征值边界可知，平时能量场景的多个RA 可表示为:

当PLL 仍采用谷时场景的参数Kp=0.60、Ki=130 时，原本位于RRA1外的GOM1 落入了平时场景中由G10 主导的谐振域RRA3，如附录B 图B1 所示。这一现象也说明了在模式谐振分析过程中考虑场景变化影响的重要性和必要性，即在某个能量场景下，稳定的GSC 参数可能在另一个场景中激发新的失稳谐振。由于子系统之间的模式谐振，闭环状态下的cEOM3 从-0.27+11.63j 被排斥到0.16+12.02j，位于附录B 图B1 的右半复平面，代表系统在小扰动下会失稳。表1 中的IRSI(EOM3)为1.593，大于1，与2.4 节分析的“失稳”谐振一致，说明了RSI的作用及有效性，即RSI 可以有效衡量模式谐振对系统稳定性的影响。在与谷时场景相同的负荷扰动下，系统的时域仿真结果如附录B 图B2 所示，PCC处频率和G10 有功功率在扰动后出现了明显的发散失稳现象。

平时场景下的另一组PLL 参数为Kp=0.80、Ki=100，在 此 参 数 下，GOM1 在RRA2和RRA3之 外，见 附 录B 图B1。根 据 表1 可 知，IRSI(EOM3) 为0.481，表示较弱的模式谐振强度，附录B 图B2 所示时域仿真结果亦表明系统在扰动后是缓慢收敛的。

RAC 方案将该场景下的IRSI(EOM3)优化至0.046，如附录B 图B3 所示，此时对应的最优PLL 参数为Kp=1.81、Ki=160。优化后的GOM1 位于附录B 图B1 中距离RRA2和RRA3较远的位置。如附录B图B2 所示，在此优化参数下系统频率和G10 有功功率在扰动后迅速收敛。

3.3 负荷峰时能量场景：10 台同步机在线

在峰时能量场景中，图5 中的10 台同步机全部在线运行。在所研究的频率和阻尼比范围内，多机交流子系统存在4 个关键振荡模式EOM，分别为EOM4 至EOM7，见附录B 表B2。在运行约束下分别形成4 个EEA，见附录B 图B4。与前述两个能量场景分析类似，根据附录B 表B3 的4 个EEA 的特征值边界，得到峰时能量场景下的多个RA，即

如 表1 所 示，PLL 参 数Kp=0.80、Ki=100 在 平时场景中导致的模式谐振较弱，但该参数下的GOM1 落入峰时场景中的RRA6，此时IRSI(EOM6)为0.917，表示该参数在峰时场景中激发较强的模式谐振。峰时场景下的另一组PLL 参数为Kp=0.90、Ki=110，此时GOM1 位 于4 个RA 外，IRSI(EOM6)为0.416，引发的模式谐振较弱。附录B 图B5 所示时域仿真结果验证了上述分析。

RAC 方案将IRSI(EOM6)优化为0.138，如附录B 图B6 所 示，得 到 了 最 优PLL 参 数Kp=1.44、Ki=118。该参数明显削弱了系统的模式谐振，如附录B图B4 所示，此时GOM1 总体上位于与4 个RA 距离最远的位置。附录B 图B5 所示时域仿真结果进一步验证了优化效果。

4 结语

本文提出了一种RAC 方案，该方案基于所提RA 和RSI，通过优化风机的控制参数，降低了风机与多机交流系统在多能量场景下的模式谐振风险，主要特点如下:

1）采用改进的SSSM 反映系统能量场景变化对子系统振荡模式的影响；

2）采用边界函数确定系统的RA，在系统可能的能量场景变化和控制器参数变化范围内，捕捉复平面上可能发生模式谐振的区域；

3）设计RSI 衡量模式谐振强度及其对闭环系统振荡模式阻尼的影响；

4）基于所提RA 和RSI，设计了风机控制器参数优化方案，有效削弱了子系统在多能量场景下的模式谐振强度。

仿真结果表明，所提出的RAC 方案能够全面地捕捉系统在不同可能的能量场景下激发的模式谐振，衡量模式谐振的强度及其对小干扰稳定性的影响，最终通过优化控制器参数来有效避免潜在的模式谐振。在未来新能源高占比、不确定性强的新型电力系统中，RAC 方案将在多变能量场景下消除风机与电网间的模式谐振方面具有重要作用。

本文主要面向风机并网系统构建谐振域，研究风机子系统与多机交流子系统二者在多能量场景下的动态交互作用，并优化风机控制器参数达到谐振抑制的目的。接下来，可进一步验证谐振域理论的普适性，例如:基于模式谐振原理，构建多个不同子系统间的谐振域、子系统内部谐振域，进而研究不同类型新能源场站间、场站内部不同控制回路间的动态交互作用，揭示新能源高占比现代电力系统在多变场景下的失稳机理。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。