车辆荷载作用下公路桥梁耦合振动研究
2024-05-15罗浩鹏
罗浩鹏
(湖南建工交通建设有限公司,湖南 长沙 410004)
1 车桥耦合振动模型试验
1.1 车辆结构模型
汽车本质是振动原理复杂的系统,在构造模型时,根据分析目标不同,简化的方向也不同。建立汽车结构模型时,在不同的研究环境下对于汽车的自由度研究也不一样,当车辆模型位于三维空间内,则需要对车辆浮沉、俯仰和侧倾3个自由度及其车轮在竖直方向上的位移进行分析;当车辆模型基于二维平面,则成为半车模型,只需考虑车体浮沉以及俯仰2个自由度以及车轮竖直方向上的位移自由度即可。
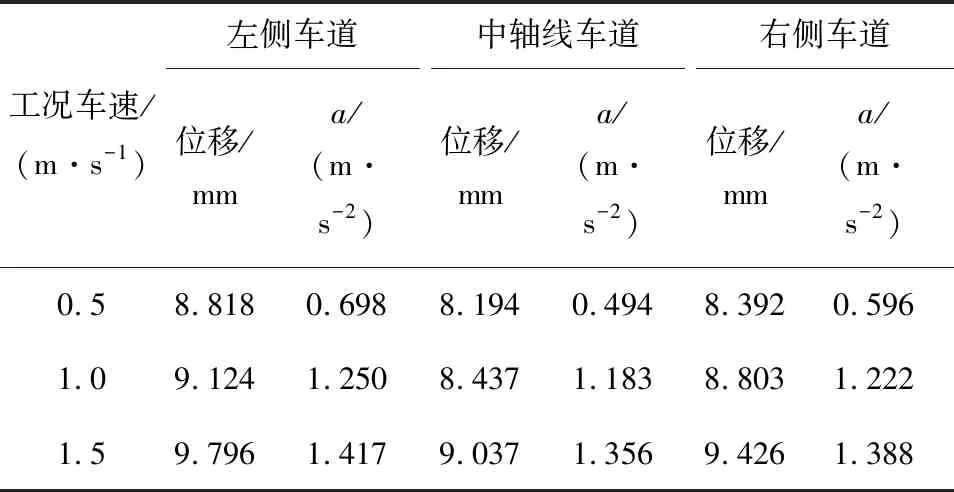
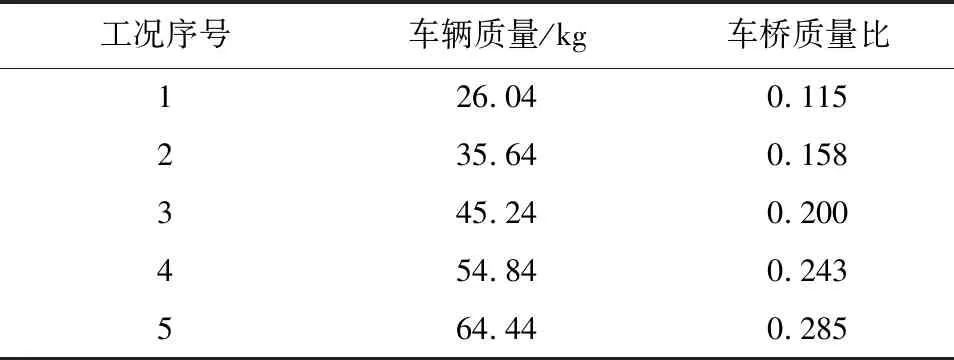
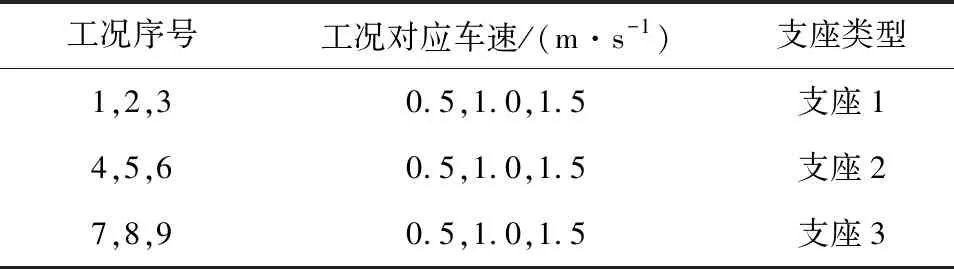
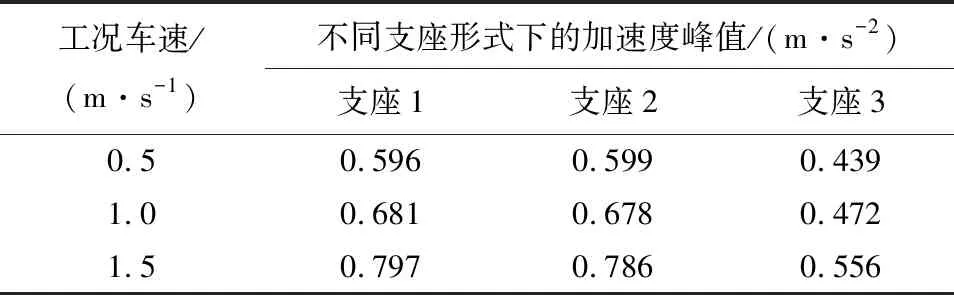
如图1所示,这时的汽车大致可简化为刚体,并由此对该两轴汽车建立了基础结构模型。这里令车身质量为M,纵轴x和横轴z通过质心O,其绕两轴运动的转动惯量分别为Lx与Lz,在悬架弹簧和减振器的共同作用下,车轴车轮与车身紧密连接。此时,在各个车轮及车轴作用下,构造的非悬挂质量为mi(0 图1 汽车简化模型 图2是基于上图的两轴汽车,使用Ansys软件构造的模型,M0表示一个质量单位,K0为弹簧阻尼单元,此时的车体与悬架弹簧阻尼利用刚性梁进行连接,从而更好地传递动力,形成汽车动力系统,建立起基于汽车空间结构的平面模型。在模拟车辆过桥运动时,可以首先在桥梁不同的车道上构造不同运动状态下的车辆模型,借此形成车流状况模拟,建立起车辆在桥面运动时的工况模型。 M0—一个质量单位:K0—弹簧阻尼单元。 车辆在过桥时,其荷载与桥梁所受力有关。为了更好地测量试验数据,需要扩大车辆经过桥面时试验桥体的动力响应。因此制作试验用桥梁模型时,钢材刚度要尽可能地小,这里结合汽车大小及速度计算桥梁尺寸。最终确定桥梁长度为320 cm,宽80 cm,厚1.4 cm,桥梁材料采用235钢,钢板总质量为225.96 kg。整个桥梁共分为三跨,左右两侧为单跨,桥梁底座至梁端保证15 cm左右的高度,将以中轴线为基准的中间跨设置为测试单元,为了更好地获取试验数据,将桥梁左端设为车辆行驶加速段,右端则相反。为了印证该桥梁模型的适用性,在试验中不仅需要分析其静力,还要通过相关试验数据分析归纳桥梁自身特性。通过Ansys进行相关理论模型建造,两端支座使用简支约束的方式,最终形成共计127个节点、216个单元的模型。 为了试验数据的对比,配重块采取标准的10 kg,在测量待测桥梁的跨中挠度时,要采用百分表辅助。试验中要使用橡胶小锤不断轻敲桥身,使其处于自由振动状态。在分析桥梁自振状态时,可以使用压电传感器,在该桥梁的支点、四分之一跨以及中轴线处设置测试点。在分析桥梁自振加速度时,可以采取频谱分析的方式,图3是试验获取的桥梁一阶竖向自振频率,表1为桥梁模型跨中挠度试验及理论值对比。 表1 桥梁模型跨中挠度试验及理论值 图3 桥梁一阶竖向自振频率 由图3可见,扰度系数在国标2018标准范围0~0.8之内,表明实际测量值优于理论值,符合承载设计要求,因此该桥梁模型适用于之后的车桥耦合振动分析。 车桥耦合振动系统需要车辆以及桥梁共同结合,通过改变车辆行驶状态、行驶车道等方式获取不同的研究数据。该系统的正常运作主要来源于其配置的动力系统,动力系统主要由电机牵引装置、制动配重等构件组成。为了满足试验需求,需要在桥梁模型的桥面上加设加减速跑道及试验车道。 在车桥耦合振动试验过程中,由电动机动力系统带动,模型上装配的钢丝绳受力开始运转,在定滑轮的辅助下带动车辆前进,试验车辆装配调速器,从而方便满足各种试验需求并对车辆行驶的状态进行调解。试验具体原理是当待测车在加速道上开始启动行驶,其驾驶速度由一开始的静止到满足试验需求的速度,然后在通过桥梁上设置的试验段时,在调速器的调节下保持匀速行驶状态,最后在减速道上停止。为了保证车辆最终停止在减速道上,在减速跑道端点处需要设置一个橡胶材质的防护装置,在触发端点处要设置配重制动设施,其目的是保证配重块在车辆处于减速状态下能够正常工作。 该试验选取车重为46.08 kg的试验车,从而计算出在车辆不同状态下车桥耦合振动情况,设置如表2所示的试验工况,桥梁左右侧车道相对于中间车道需要向外位移15 cm。 表2 设置试验工况 为了测试桥梁在不同工况下的跨中竖向加速度及其响应位移,最终测得相应试验数据如表3所示。 表3 跨中竖直方向位移及加速度 由表3可知,当待测车辆以不同速度在不同的车道行驶时,车辆速度与桥梁跨中竖向位移及其加速度的峰值呈单调关系,与竖直方向加速度相比,竖直方向位移与车速呈正相关关系。在不同的工况下,桥梁两侧车道的跨中竖直方向位移及其加速度的响应大于同环境下的中轴线车道,左侧车道的响应最为明显。其原理是当待测汽车位于桥梁左右两侧行驶时,至少有一侧车轮靠近桥梁在中轴线上的测试点位,增强了其挠度。 通过测量待测车在不同运行状态下车身竖直方向加速度的响应情况,得到如表4所示的车体竖直方向加速度数据。 表4 不同运行状态车身竖向加速度 由表4可知,待测车辆行驶速度不断增加的同时,待测汽车加速度的最高值与前者处于正相关关系,待测车辆在中轴线车道运行时,车辆竖直加速度变化幅度不大,车身在竖直方向由于受到外力从而获得的加速度最小。 综上所述,待测车辆在桥梁不同位置运行时,位于桥梁中轴线车道行驶情况下车辆耦合振动程度最轻,随着待测车辆行驶速度的增加,振动程度与行驶速度呈正相关。通过分析不同行车道位置对桥梁响应动力的关系可以得出结论,不同的行车道位置对车桥动力响应的程度并没有太大的影响,因此在后续试验中可以根据试验需要选择对应车道。 车桥质量比是车辆在载荷状况下与桥梁质量的比值。上述试验中采用的钢制桥梁,其质量经过测量为225.96 kg,在本试验中采用改变待测车辆载荷重量的方式改变车桥质量比,从而不断改变待测车辆荷载,让其质量不断变化。为了试验的严谨性,需要保证车辆在中轴线车道匀速行驶,速度暂定为1.5 m/s。经过试验得出表5所示的数据。 表5 不同工况下的车桥质量比 当待测车以 1.5 m/s的恒定速度在对应车道行驶时,通过不断改变其载荷质量,由试验可知,不断提高车辆载荷质量,增加了车桥质量比,桥梁的响应力也不断增加。车辆载荷质量大时,桥梁更容易受到响应从而振动。 通过研究可以发现,车桥质量比不断增长的同时,桥梁中间跨在竖直方向上的位移与其加速度也在相应增长。车桥质量比在从0.121向0.291不断升高时,中间跨位移的峰值也相应地由4.702 mm扩大到11.98 mm,跨中加速度最大值从0.796增大到1.363,桥梁中跨竖直方向的位移最大值与车桥质量比的增幅位于同一比例;当车桥质量比小于0.17时,桥梁跨中竖向加速度最大值大幅增长,随后增长趋势减缓。 在待测车以不同质量用相同速度行驶于桥梁试验车道时,通过试验可知,车桥质量比增长的同时,车体竖直方向加速度最大值对应减小。在车桥质量比从0.121扩大到0.163时,竖直方向加速度减小至37.52%,由此可知,车辆载荷质量增加时,车身趋于稳定,振动幅度减弱。 综上所述,车桥质量比影响着车桥动力响应的状况。在试验中,为了使桥梁和车身振动更加明显,可以将车桥质量比的范围确定在0.10~0.17之间。 试验中采用常用的三种支座形式进行试验分析。支座1为一端垫块,另一端采用滚轴支座;支座 2采用两端垫块;支座3两端平整。选用试验车以不同的行驶速度在不同支座桥梁中轴线车道行驶,试验条件如表6所示。 表6 工况、车速及支座类型 在桥梁支座形式不同时,令测试车以恒定速度过桥,从而激发桥梁竖向动力响应,由桥梁跨中竖向位移以及加速度峰值情况可知,在车辆行驶速度不断增加时,对于不同支座桥梁的响应动力逐渐增大。在行驶速度恒定时,支座3桥梁跨中竖直方向的位移最大值最小,其相比支座1,峰值最大值减少了27.03%;支座3桥梁的跨中竖向加速度峰值最大,相比于支座 1,峰值最大增长了21.04%。通过对待测车辆基于不同工况的竖直加速度响应的试验研究,得到如表7所示的试验数据。 表7 不同速度下不同支座形式的车体竖向加速度峰值 由表7可知,在行驶速度不断增加的同时,不同桥梁支座形式的车身竖直方向加速度呈增长趋势。在车辆行驶速度恒定时,桥梁采用支座3形式下的车身竖直加速度最小,相比于支座1,最大减少了26.29%。 桥面不平度是指桥梁表面基于标准面的偏移程度,也影响着车桥耦合振动的程度。在桥面统计特性描述时,通常使用功率谱密度。基于《车辆振动输入路面平度表示方法》建议的如下拟合表达式,利用MATLAB软件编程模拟不同等级的桥面不平度样本。 式中:n0为空间参考频率,n为实际空间频率;Gx为路面功率谱密度值,又被称作路面不平整度值,它受桥面不同等级制约;ω为指数常数,一般取2。 (1)车桥模型的一阶竖向自振频率,其测量值大致与理论值相等,因此适用于后续车桥耦合振动分析。 (2)待测车辆在不同车道行驶时,位于中间的车道所受的振动响应最小,在车辆行驶速度逐渐递增的同时,行驶速度与桥梁的振动响应度呈正相关趋势。在试验过程中,车道产生10 cm的位移不足以对车桥模型试验造成影响,因此在选择行车道时可以基于不同研究目的来进行选择。 (3)车桥质量比是车桥耦合振动的一个重要制约因素。将车桥质量比选择为0.10~0.17可以使桥梁和车体振动响应更加明显。 (4)桥梁的支座形式对于车桥结构响应的振动力影响较大,当桥梁的底座采取支座1的模式时,桥梁具有比较明显的竖直方向加速度响应。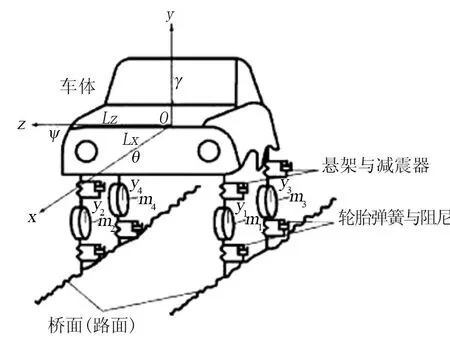

1.2 桥梁模型


1.3 车桥耦合振动试验系统
2 试验参数分析
2.1 行车道位置影响


2.2 车桥质量比的影响
2.3 桥梁支座形式的影响
3 桥面不平度模型及其模拟
4 结 论
