混合动力汽车深度强化学习分层能量管理策略

戴科峰 胡明辉

摘要：为了提高混合动力汽车的燃油经济性和控制策略的稳定性，以第三代普锐斯混联式混合动力汽车作为研究对象，提出了一种等效燃油消耗最小策略（equivalent fuel consumption minimization strategy，ECMS）与深度强化学习方法（deep feinforcement learning，DRL）结合的分层能量管理策略。仿真结果证明，该分层控制策略不仅可以让强化学习中的智能体在无模型的情况下实现自适应节能控制，而且能保证混合动力汽车在所有工况下的SOC都满足约束限制。与基于规则的能量管理策略相比，此分层控制策略可以将燃油经济性提高20.83%～32.66%；增加智能体对车速的预测信息，可进一步降低5.12%的燃油消耗；与没有分层的深度强化学习策略相比，此策略可将燃油经济性提高8.04%；与使用SOC偏移惩罚的自适应等效燃油消耗最小策略（A-ECMS）相比，此策略下的燃油经济性将提高5.81%～16.18%。

关键词：混合动力汽车；动态规划；强化学习；深度神经网络；等效燃油消耗

中图分类号：U471.15          文献标志码：A           文章编号：1000-582X（2024）01-041-11

Deep reinforcement learning hierarchical energy management strategy for hybrid electric vehicles

DAI Kefeng， HU Minghui

（College of Mechanical and Vehicle Engineering， Chongqing University， Chongqing 400044， P. R. China）

Abstract： To improve the fuel economy and control strategy stability of hybrid electric vehicles （HEVs）， with taking the third-generation Prius hybrid electric vehicle as the research object， a hierarchical energy management strategy is created by combining an equivalent fuel consumption minimization strategy （ECMS） with a deep reinforcement learning （DRL） method. The simulation results show that the hierarchical control strategy not only enables the agent in reinforcement learning to achieve adaptive energy-saving control without a model， but also ensures that the state of charge （SOC） of the hybrid vehicle meets the constraints under all operating conditions. Compared with the rule-based energy management strategy， this layered control strategy improves the fuel economy by 20.83% to 32.66%. Additionally， increasing the prediction information of the vehicle speed by the agent further reduces the fuel consumption by about 5.12%. Compared with the deep reinforcement learning strategy alone， this combined strategy improves fuel economy by about 8.04%. Furthermore， compared with the A-ECMS strategy that uses SOC offset penalty， the fuel economy is improved by 5.81% to 16.18% under this proposed strategy.

Keywords： hybrid vehicle; dynamic programming; reinforcement learning; deep neural networks; equivalent consumption minimization strategy

車辆传动系统的电气化是未来可持续发展中的重要环节。但就现阶段而言，纯电动汽车的电池技术还未实现突破；混合动力汽车（hybrid electric vehicle，HEV）的节油潜力也没有得到充分发挥，设计良好的能量管理策略可以提高节油率。

混合动力汽车最优能量管理的经典数值计算方法有2种：一是基于系统模型的动态规划（dynamic programming，DP）；二是庞特里亚金极值原理（Pontryagins minimal principle，PMP）[1]。其中，DP近似求解哈密尔顿-雅可比-贝尔曼方程以得到最优控制问题在离散时间的最优解。DP需要获得完整的驾驶工况信息且计算负荷高，因此现阶段仅用DP的离线计算来导出控制规则[2]。等效燃油消耗最小策略（equivalent consumption minimization strategy，ECMS）是以PMP为理论基础的一种实时优化能量管理策略。它将全时域最优控制问题转化为了基于等效因子的瞬时优化问题，在确定等效因子后，便于能量管理问题的实时求解[3-7]。对于不同的驾驶工况，合适的等效因子需要通过大量的离线仿真才能获得，难以根据实际驾驶场景进行实时求解，因而ECMS实时效果差。

自人工智能进入最优控制领域以来，深度强化学习（deep reinforcement learning，DRL）已经成为了一种常用的控制策略，正在被广泛地应用于混合动力汽车的传动系统控制[8-12]。Qi等[13]在能量管理中采用了深度q学习，不仅可以解决传统q学习中出现的“维数灾难”，而且证明了深度强化学习比q学习具有更好的燃油经济性。Zhang等[14]的研究表明，基于经验回放的深度q网络在经过充分训练后，即使在不熟悉的驾驶循环工况中，也能得到比动态规划更好的燃油经济性。但是这些基于深度强化学习方法的能量管理策略会由于探索和环境扰动等不确定性因素，导致最终的控制策略不稳定，从而无法在实车上直接使用。

ECMS策略可以将全局最优问题转化为瞬时优化问题，简化了能量管理问题的求解。考虑到在持续变化的工况中，难以获取ECMS策略最佳等效因子的问题，综合能量管理所需的控制策略特性，笔者提出了一种将深度强化学习算法和ECMS策略结合的分层控制策略。上层算法采用基于工况数据的深度强化学习方法来选择最佳等效因子；下层算法基于等效燃油消耗最小的控制目标来实现最优功率分配。这种分层控制策略方法可以充分利用深度强化学习的探索性以及ECMS策略的鲁棒性，从而提高混合动力汽车的燃油经济性和能量控制策略的稳定性。

1 混合动力系统建模

强化学习的原理如图1所示。基于强化学习的能量管理智能体学习过程为：1）在特定工况下，能量管理智能体生成动作作用于混合动力汽车的仿真模型；2）HEV环境计算状态变化和奖励函数；3）智能体在交互中改进策略。本节将针对强化學习的交互仿真环境和混合动力系统进行建模。

1.1 车辆准静态模型

第三代Prius的传动系统结构如图2所示。传动系统包含3个驱动装置，分别是发动机（ICE）、发电机（MG1）和驱动电动机（MG2）；包含2个行星齿轮单元。符号S表示太阳轮，C表示行星架，R表示齿圈。发动机将单向离合器与第一行星架相连，然后依次连接第一齿圈、减速器和差速器，从而驱动车辆。发电机连接到第一行星排的太阳轮，调节发动机的转速。驱动电动机与第二行星排的太阳轮连接，行星架C2是固定的，驱动电机经过减速增扭后在齿圈处与发动机实现转矩耦合。

根据驱动力与外部阻力平衡的力学原则[15]，车辆的动力学模型表达式可以写为

{（F_w=F_a+F_r+F_g+F_f，@F_a=mv ˙=ma，@F_r=1/2 ρAC_D v^2，@F_g=mgsin（α），@F_f=μ_r mgcos（α）。）┤   （1）

式中：F_w为驱动力；F_a为惯性力；F_r为空气阻力；F_g为坡度阻力；F_f为滚动阻力；a为加速度；ρ为空气密度；A为迎风面积；C_D为空气阻力系数；v为车辆相对速度；μ_r为滚动阻尼系数。整车的主要结构参数如表1所示。

1.2 驱动部件模型

发动机的万有特性图与电动机的二维效率曲面图分别如图3（a）和图3（b）所示。当发动机的需求功率P_e小于500 W时，可以直接关闭发动机，相应的油耗模型为

m ˙_fuel={（G（P_e）@0）┤ （，P_e>500；@，P_e≤500。）   （2）

式中：m ˙_fuel表示燃油消耗率；G为插值查表的方法；P_e为发动机功率。对于电机而言，所需电机功率P_m则为

P_m={（T_m?ω_m/（G_m （T_m，ω_m））@T_m?ωm?G（T_m，ω_m））┤ （，P_m>0；@，Pm≤0。）      （3）

式中：ω_m表示电机转速；T_m表示电机扭矩。

1.3 电池模型

采用一阶等效电路模型来描述镍氢电池的动态特性，同时忽略温度变化和电池老化的影响，电池的动态方程可以描述为

{（P_batt （t）=V_oc I_b （t）-r_int I_b 〖（t）〗^2，@I_b （t）=（（V_oc-√（V_oc^2-4r_int P_m （t））））/（2r_int ），@x ˙_SOC=-（I_b （t））/Q_nom  。）┤   （4）

式中：P_batt、I_b分别指电池的功率、电流；V_oc为开路电压；r_int为电池内阻；Q_nom指电池标称容量；x_SOC表示电池的荷电状态。完整的电池模型参数如表2所示。

2 深度强化学习分层能量管理策略

本节阐述了将深度强化学习和ECMS策略相结合的分层混联HEV能量管理方法。

2.1 自适应等效燃油消耗策略

Paganelli[16]在1999年引入了等效燃油消耗最小的启发式方法来求解能量管理问题，该方法后来受到了广泛应用。该启发式方法的核心思想为：在充电和放电过程中电能的使用与燃油消耗相关联，将电能消耗转化为油耗，总的瞬时当量油耗为

m ˙_（f，eqv） （t）=m ˙_f （t）+m ˙_ress （t）， （5）

式中：m ˙_（f，eqv）表示等效当量油耗，g/s；m ˙_f （t）为实际发动机燃油消耗量，g/s；m ˙_ress （t）电能消耗的等效油耗，g/s。

m ˙_ress （t）=（s（t））/Q_lhv  P_batt （t）=K_eq （t）?P_batt （t），   （6）

式中：s（t）为虚拟燃油消耗因子；Q_lvh为汽油最低热值，MJ/kg；P_batt为电池功率；K_eq （t）为等效因子。

在自适应等效燃油消耗策略中，等效因子可以在驾驶工况中作为荷电状态的函数进行不断更新。这种自适应的反馈调节可以很好地维持电池的荷电状态，但不能保证能量的最优分配[17-18]。自适应等效燃油消耗（adaptive-ECMS， A-ECMS）常用的等效因子惩罚函数为

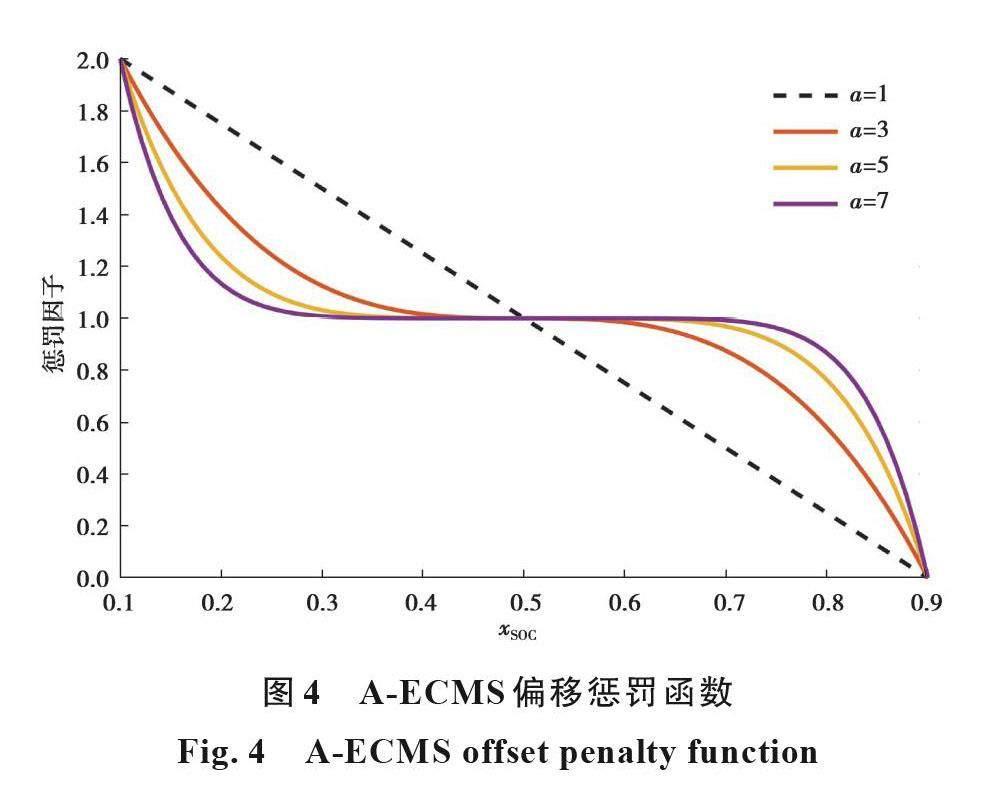
p（x_SOC）=1-[（x_SOC （t）-x_SOCref）/（（x_SOCmax-x_SOCmin）/2）]^a。  （7）

式中：x_SOCmax和x_SOCmin分别为电池荷电状态的上限和下限。

图4为不同幂取值下的荷电状态偏移惩罚函数。

在已知等效因子的情况下，可采用式（8）直接搜索瞬时等效油耗最优的发动机功率点，为

π（P_eng^*）=min┬（π∈Π） [m ˙_（f，eqv） （t）=m ˙_f （t）+K_eq （t）?P_b]，      （8）

式中：K_eq （t）=λ_DDPG?P（b_SOC）?F ?_C/η ?_t，λ_DDPG为需要学习得到的变量；P（b_SOC）表示在危险荷电状态下的惩罚系数，它是嵌入到仿真环境当中的；F ?_C表示平均燃油消耗，取235 g/（kW·h）；η ?_t=η ?_char?η ?_dis表示平均充电与平均放电效率，即电能转换效率，取值0.7。

2.2 基于深度强化学习的等效因子获取方法

2.2.1 深度强化学习算法框架

深度确定性策略梯度算法（deep deterministic policy gradient， DDPG）可以实现能量管理中连续动作的输出。该算法由2个独立的深度神经网络构成，是一种具有演员-评论家结构的确定性策略梯度算法，用“演员”来选择控制策略，用“评论家”来评估所采用的控制策略优劣。

“评论家”网络是基于最优动作值函数Q^* （s，a）完成设计的。该动作值函数的递推关系为贝尔曼方程

Q^* （s，a）=E┬（s^'～P） [r（s，a）+γ max┬（a^' ） Q^* （s^'，a^'）]Q^* （s，a）=E┬（s^' ）， （9）

式中：r为奖励；γ为折扣因子；s^'指从环境中采样得到的下一时刻状态。

若采用神经网络作为函数拟合器来逼近Q^* （s，a）函数，那么就需要对参数?进行不断地学习和改进。因此，可定义为贝尔曼均方误差函数：

（L（?，D）=E┬（（s，a，r，s^'，d）～） [（Q_? （s，a）-（r+γ（1-d）max┬（a^' ） Q_? （s^'，a^' 〖）））〗^2]=@E┬（（s，a，r，s^'，d）～） [（Q_? （s，a）-（r+γ（1-d）Q_（?_target ） （s^'，μ（s^' 〖））））〗^2]。）    （10）

式（10）描述了参数化策略网络对贝尔曼方程的逼近程度。“评论家”网络更新的步骤为：先从经验池中采样，得到转移数据对（s，a，r，s^'，d）；然后调用Adam优化器对式（10）进行优化。

DDPG中的“演员”通过学习一个确定性策略μ（s|θ^μ）来将“评论家”的打分进行最大化，即最大化动作值函数Q_? （s，a）。式（11）表示网络参数的变化，并使用梯度上升方法来更新。

Δθ=max┬θ  E┬（s～D） [Q_? （s，μ_θ （s））]。   （11）

2.2.2 状态空间

智能体与环境交互是基于状态观测完成的，环境为车辆仿真模型。在混合动力汽车能量管理问题中，智能体通常采用3个参数作为状态量[10]，即：车速v_veh、加速度a_veh和电池的荷电状态x_SOC，为进一步降低燃油消耗，笔者增加了未来20 s的平均车速a_ave为状态变量，状态空间为

S_imp=[v_veh，a_veh，x_SOC v_ave]。     （12）

2.2.3 动作空间

动作空间at为

a_t=λ_DDPG，  （13）

式中，λ_DDPG∈[0，1]，为分层策略中上层算法输出的归一化参数。

2.2.4 奖励函数

实时奖励函数是深度强化学习算法的重要组成，它会直接影响深度神经网络的参数更新。同时考虑到能量管理控制策略的目的是降低燃油消耗，提高车辆的燃油经济性，并且将电池荷电状态x_SOC维持在安全范围内，因此将实时奖励Rt定义为

R_t=-∑_（t=0）^（T_f-1）?。    （14）

奖励函数由2部分组成：第一部分为m ˙_（fuel_t ）瞬时燃油消耗率；第二部分是当前时刻的电池荷电状态与参考荷电状态间的偏差，它代表了维持电池电量平衡的成本。C_1是荷电状态偏移的惩罚因子，将其设置为常数。

2.3 分层策略算法的实现流程

ECMS的启发式特性可以对能量管理的决策过程进行简化，从而在一维的搜索空间下进行快速决策。但ECMS中的等效因子对于工况的变化较为敏感，如何确定最佳等效因子是ECMS方法中的难点。传统的解决办法是在标准工况下进行多次仿真，离线计算特定工况下的最佳等效因子并在实际运行过程中查表。这种方法不仅工作量巨大，而且在不同工况下的节油效果也相差较大。因此笔者提出了一种分层能量管理策略：上层采用无模型的强化学习方法——DDPG，通过学习的方法自适应获得最佳的等效因子；下层使用一维搜索来快速确定最佳的发动机功率。该策略算法的完整实现流程如图5所示。

3 验证与讨论

为了验证等效燃油消耗最小策略和深度强化学习方法相结合的分层能量管理策略，笔者在Python中搭建了系统的仿真环境。设置电池的充放电区间为20%～80%，并将分层策略与全局优化DP算法、基于规则的控制策略（rule-based，RULE）和直接控制发动机功率的深度强化学习控制策略（power-DDPG，P-DDPG）分别进行了对比试验。其中，分层策略（two level-DDPG，T-DDPG）可以分为三特征策略和四特征策略，分别简写为T3-DDPG和T4-DDPG。T4-DDPG在T3-DDPG的基础上添加了未来车速信息作为第四特征量。最后采用重庆地区的实测工况作为测试集，来验证此分层策略对于工况的适应性。

3.1 算法参数设计与收敛分析

深度强化学习方法DDPG包含了4个深度神经网络，2个值函数网络（“评论家”）和2个策略网络（“演员”）。4个神经网络均包含3层全连接隐藏层，宽度分别为256、128、64。训练过程的超参数设置见表3所示。

图6为3种基于深度强化学习算法的智能体在NEDC工况下的训练过程。从图中可以看出，相比于的P-DDPG算法，加入了ECMS底层算法的分层控制策略在不同种子设置下的表现更加稳定，其中以T4-DDPG策略应对扰动的稳定性表现最好。从油耗上看，添加了未来20 s内平均车速信息的T4-DDPG策略所对应的燃油消耗最低，为3.65 L·（100 km）-1。

3.2 电池充放电荷电状态轨迹分析

分层控制策略中，下层算法采用的是ECMS来实现最优功率的分配，所以等效因子是下层算法的重要参数。针对传统的常等效因子进行WLTC工况下的ECMS策略研究分析，得到如图7所示的荷电状态轨迹。从图中不同常等效因子下对应的荷电状态轨迹可以看出，不论如何对常等效因子的数值进行调整，该方法在固定工况下的表现都会与DP相差较大，其表现不能达到令人满意的水平，因此需要采用基于学习的策略对等效因子进行实时调整。

图8为NEDC工况下的T3-DDPG策略、T4-DDPG策略和A-ECMS策略的等效因子的学习情况。从图中可以看出，A-ECMS策略下的等效因子经过荷电状态偏移矫正后，一直维持在一个较高的水平，导致用电成本较高。而无论是三参数还是四参数的智能体，在平均车速较低的工况中会给电能一个较小的等效因子，用电成本更低。所以车辆倾向于使用电能，因而在低速区使用纯电模式。当平均车速较高时，智能体倾向于输出更高的等效因子，导致用电的成本增加；在此时采用发动机和电池的混合驱动模式更佳。而随着车速进一步提高，电量的成本进一步升高，与此同时发动机的功率会变得更高。相较于T3-DDPG策略，添加了未来车速信息的T4-DDPG策略表现出更好的鲁棒性，对于车速变化较大的场景，它能够降低等效因子的抖震。

图9为分层控制策略和其他控制策略在双NEDC工况下电池荷电状态的变化曲线。从图中可以看出，基于规则的控制策略随着驱动功率的突然增加，其荷电状态有较为明显的波动；而P-DDPG策略在双NEDC工况下，发生了电池荷电状态超出预设范围的情况，大量的低功率路段，导致了智能体在工况中学习策略失败；对于A-ECMS策略而言，由于增加了一个等效因子对荷电状态的偏移校正系数，可以将电池荷电状态维持在预设范围；表现最好的是T4-DDPG分层策略，其荷电状态轨迹与基于DP策略的性能表现最为吻合。

3.3 能量管理策略节油效果分析

为了验证分层控制策略的节油效果，笔者在大量标准工况下进行了仿真分析。图10为不同工况下各控制策略的油耗表現。从图中可以看出，T4-DDPG策略的节油效果与动态规划的节油效果最为接近的。与P-DDPG相比，T4-DDPG策略将燃油经济性提高了3.05%～8.22%；与基于规则的能量管理策略相比，T4-DDPG将燃油经济性提升了20.83%～32.66%；与A-ECMS相比，T4-DDPG策略将燃油经济性提高了5.81%～16.18%。

为了验证该分层控制策略对未知工况的适应性，笔者采用重庆地区的实测道路工况作为所提出策略的测试集。测试集中由于实测的车速信息存在噪声，所以对其进行滑动平均和滤波处理。处理后的测试工况数据集如图11所示。

图12为分层控制策略在实际道路工况下的表现，红色曲线为测试表现，蓝色曲线为训练表现。其中基于标准工况训练得到的T4-DDPG策略在此实测工况下的百公里油耗为4.04 L，基于标准工况训练得到的T4-DDPG策略在实际道路的百公里油耗为3.98 L，两者差值很小。综上所述，该分层控制策略对未知工况的适应性较强，可适用于不同的工况。

4 结束语

分层控制策略不仅可以解决传统ECMS策略中等效因子难以确定的问题，而且还能解决深度强化学习方法中由于探索和干扰带来的不稳定性问题。在多种标准工况下的仿真结果表明，该分层控制策略中的智能体能够学习到一个良好的控制策略，在所有工况下车辆的电池荷电状态都能满足约束条件。除此以外，笔者所提出的分层控制策略算法具有无模型的特性，所以能够迁移至其他构型的混合动力汽车进行能量管理策略的开发。最后，仿真结果进一步表明了经过大量工况训练后的智能体对各种不同的未知工况具有较强的适应性，使得该分层控制策略具有非常重要的实际应用价值。

参考文献

［1］  Onori S， Serrao L， Rizzoni G. Hybrid electric vehicles： energy management strategies[M]. London： Springer London， 2016.

［2］  Scordia J， Renaudin M D， Trigui R， et al. Global optimisation of energy management laws in hybrid vehicles using dynamic programming[J]. International Journal of Vehicle Design， 2005， 39（4）： 349.

［3］  Liu J M， Peng H E. Control optimization for a power-split hybrid vehicle[C]//2006 American Control Conference. IEEE， 2006： 6.

［4］  Musardo C， Rizzoni G， Guezennec Y， et al. A-ECMS： an adaptive algorithm for hybrid electric vehicle energy management[J]. European Journal of Control， 2005， 11（4/5）： 509-524.

［5］  Serrao L， Onori S， Rizzoni G. ECMS as a realization of Pontryagins minimum principle for HEV control[C]//2009 American Control Conference. IEEE， 2009： 3964-3969.

［6］  Rezaei A. An optimal energy management strategy for hybrid electric vehicles[D]. Houghton， Michigan： Michigan Technological University， 2017.

［7］  Sun C， Sun F C， He H W. Investigating adaptive-ECMS with velocity forecast ability for hybrid electric vehicles[J]. Applied Energy， 2017， 185： 1644-1653.

［8］  Hu X S， Liu T， Qi X W， et al. Reinforcement learning for hybrid and plug-In hybrid electric vehicle energy management： recent advances and prospects[J]. IEEE Industrial Electronics Magazine， 2019， 13（3）： 16-25.

［9］  Zhao P， Wang Y Z， Chang N， et al. A deep reinforcement learning framework for optimizing fuel economy of hybrid electric vehicles[C]//2018 23rd Asia and South Pacific Design Automation Conference （ASP-DAC）. IEEE， 2018： 196-202.

［10］  Lian R， Peng J， Wu Y， et al. Rule-interposing deep reinforcement learning based energy management strategy for power-split hybrid electric vehicle[J]. Energy， 2020， 197： 117297.

［11］  Hu Y E， Li W M， Xu K， et al. Energy management strategy for a hybrid electric vehicle based on deep reinforcement learning[J]. Applied Sciences， 2018， 8（2）： 187.

［12］  Wang Y， Tan H C， Wu Y K， et al. Hybrid electric vehicle energy management with computer vision and deep reinforcement learning[J]. IEEE Transactions on Industrial Informatics， 2021， 17（6）： 3857-3868.

［13］  Qi X W， Luo Y D， Wu G Y， et al. Deep reinforcement learning-based vehicle energy efficiency autonomous learning system[C]//2017 IEEE Intelligent Vehicles Symposium （IV）. IEEE， 2017： 1228-1233.

［14］  Zhang Z D， Zhang D X， Qiu R C. Deep reinforcement learning for power system applications： an overview[J]. CSEE Journal of Power and Energy Systems， 2019， 6（1）： 213-225.

［15］  余志生. 汽車理论[M]. 5版. 北京： 机械工业出版社， 2009.

Yu Z S. Automobile theory[M]. 5th ed. Beijing： China Machine Press， 2009.（in Chinese）

［16］  Paganelli G. Conception et commande dune cha?ne de traction pour véhicule hybride parallèle thermique et électrique[D]. Famars： Université de Valenciennes， 1999.

［17］  Paganelli G. A general formulation for the instantaneous control of the power split in charge-sustaining hybrid electric vehicles[C]// Proceedings of AVEC 2000， 5th Int. Symp. on Advanced Vehicle Control. 2000.

［18］  Onori S， Serrao L， Rizzoni G. Adaptive equivalent consumption minimization strategy for hybrid electric vehicles[C]//Proceedings of ASME 2010 Dynamic Systems and Control Conference. IEEE， 2011： 499-505.

（编辑  詹燕平）