不凝性气体对纳米通道内水分子流动传热影响的分子动力学模拟*

邢赫威 陈占秀 杨历 苏瑶 李源华 呼和仓

(河北工业大学能源与环境工程学院,天津 300401)

随着电子元件高性能化和小型化的发展,纳米通道内工质的流动传热问题受到了更多的关注.本文采用分子动力学模拟方法,模拟了300,325,350 K 的纳米通道中流体的流动传热情况,工质为水,水中不凝性气体用氩气代替.结果表明: 流动过程中,氩原子形成高势能团簇,随着温度升高,流体势能上升,团簇逐渐减小或消失;少量气体原子能够促进流动,而较多氩气会导致通道中心区域形成较大气体团簇而阻碍流动,同时,被加热的工质能显著减小流动阻力系数;近壁面区域流体温度高于中心区域,团簇内部原子活动更加剧烈,平均分子动能更大,温度更高;水的氢键结构可以促进纳米通道内的传热,氩原子会影响氢键数量,高温会破坏水分子形成的氢键网络,使努塞尔数下降.本研究分析了不凝性气体影响下微通道内水分子流动传热的机理,为电子设备的强化传热提供了理论指导.

1 引言

随着微纳米科学技术的不断发展,电子器件的性能需求日益增加[1].微纳米处理技术的进步使计算机芯片的运算速度大幅增大,但芯片产生的热量也剧烈升高[2].为了满足高性能芯片的冷却需求,微纳米通道中流体的散热问题受到越来越多研究学者的重视.然而在微尺度下,物质运输与能量传递都被限制在一个狭小的空间内,在分子力效应、表面张力效应等多种微尺度效应的作用下,实验的测量精度受到很大的限制,宏观尺度下流体流动规律的原理不再适用[3,4].为了更好地对纳米通道进行分析,研究者把目光转向分子动力学方法.分子动力学方法从微观原子运动的角度出发,运用计算机模拟技术准确地描述分子之间的作用力,并且不受时间与空间的限制,对揭示微观层面机制提供了新的视角.因此,分子动力学方法成为当前研究微纳米通道中流动传热问题的主要方式[5].

在纳米尺度下,壁面效应能够对流道内工质的流动产生较大影响,很多学者对纳米通道内流体的流动情况和输运特性进行了深入研究.Shi等[6]采用分子动力学方法研究了表面润湿性与数密度之间的关系,结果表明随着表面润湿性的提高,密度振荡的幅度更大,密度峰和密度谷之间的间距缩短,密度振荡行为更加明显.Voronov等[7]研究了流体的Couette 流动,发现当固体壁面与流体之间的接触角超过某一特定值时,接触角的增大会导致滑移长度的减小.Zhang 和Chen[8]研究了三维Couette 流动系统中的界面速度滑移,结果表明,无论液体在横向还是纵向流动,粗糙表面都会引起额外的能量损失,并导致纳米通道中界面速度的降低.Priezjev[9]研究了表面能和剪切速率对简单流体流动中滑移长度的影响,发现在弱壁面-流体相互作用下,滑移长度随剪切速率呈非线性关系.Semiromi 和Azimian[10]设置了不同驱动力作用下的流动模型,发现平均轴向速度在通道中心线附近具有对称分布,并且外部驱动力的增大可以增大流体的最大和平均速度值,此外,还发现滑移长度和滑移速度是驱动力的函数.

纳米通道内流体的传热问题也引起了诸多学者的关注.Markvoort等[11]使用分子动力学研究了润湿性对界面热输运性质的影响,结果表明,润湿性的提高有利于原子之间的热传递.Zhou等[12]构建了铜原子壁面与氩原子流体间的传热模型,结果表明,即使对于超亲水表面,固-液相互作用强度的增大仍然能够显著增强核沸腾传热性能.Bao等[13]研究了光滑热基底约束的薄液膜中滑移长度随温度和速率的变化规律,发现对于亲水壁面和疏水壁面,流体的温度都会随着剪切速率的上升而升高.Ge等[14]模拟热流体流过冷壁面的纳米通道,发现努塞尔数随着流体与壁面之间作用力的增强而升高,表明对流换热可以通过增加表面润湿性增强.Yao等[15]建立了恒定壁面温度下纳米通道内的对流换热模型,研究了固-液相互作用力对流动和传热特性的影响,发现相互作用能够在一定范围内有效提高整体的传热性能,如果相互作用力继续增大,流动阻力的显著增大将削弱纳米通道整体传热性能的提高.

目前,对于纳米通道中的流动传热问题,大多数研究选取了简单原子作为流动工质.水作为实际工程应用广泛的流体,其流动与传热特性也受到了学者们的关注.Alkhwaji等[16]采用分子动力学方法对水分子的热力学性质进行了研究,并与实验结果进行了比较,结果表明,模拟水分子的导热系数、黏度、密度、比热容、比热压、普朗特数和体积热膨胀系数均于实验结果相当接近,证明了分子动力学模拟的有效性.Hong等[17]通过模拟发现液态水分子中存在具有一定间距的纳米气泡团.Xi等[18]研究了固体壁面与水分子间的传热机理,结果表明,增大相互作用强度有利于水分子形成氢键网络,从而增强界面传热.

综上所述,目前研究水分子作为工质的纳米通道流动传热问题还不够详细,而考虑纳米气泡对水分子热力学与动力学性质影响的研究更是较少.本文采用分子动力学模拟方法,构建了水分子掺入不凝性气体情况下的流动传热模型,选用氩这一单原子分子作为气体原子,以达到简化计算与提高计算精度的目的.通过设置5 种不同氩原子含量的流体,在300,325,350 K 的热源温度下,对流体工质的流动与传热性能进行了深入研究,并通过分析气体团簇的变化,揭示其影响机理.

2 仿真模型和模拟设置

2.1 物理模型和模拟方法

纳米通道内流体流动的模型如图1 所示.仿真模型的尺寸为15 Å × 110 Å × 80 Å (x×y×z).纳米通道壁面由铜原子构成,按照面心立方结构(FCC)进行排列,晶格常数为3.62 Å.初始流动模型如图1 所示,Z方向上最外层的两层铜原子(绿色原子层)是固定的,厚度为3.62 Å,用于防止模型在运算期间发生迁移或变形;临近最外层的两层铜原子(橙色原子层)为加热层,厚度为3.62 Å,被用作热恒温器,由Langevin 恒温器控制;内层原子(黄色原子层)与流体接触,起到导热作用;加热层与导热层的铜原子受弹簧力约束,以便铜原子在模拟过程中交换能量时能够维持在其原始位置振动,弹簧力大小为-Kr,其中K是弹簧常数,大小为0.426 eV/nm,r是原子实际位置于原始位置之间的距离.流体区域由水分子和氩原子组成,其中红色原子为氧原子,白色原子为氢原子,蓝色原子为氩原子,均匀分布于间距为H=50 Å的固体壁面之间,流道内的原子数量如表1 所列.流体在外力F的作用下沿Y方向流动,为提高模型的真实性和系统的稳定性,在X,Y,Z方向上采用周期性边界条件.

表1 流道内的粒子数量Table 1. Number of particles in the channel.

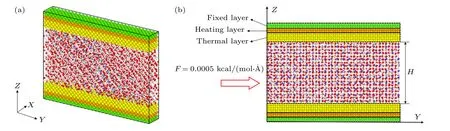
图1 模拟系统图Fig.1.Simulation system.

在本模拟中,水分子模型采用TIP4P 模型,该模型在化学键H—O—H 夹角的对角线上距离氧原子0.0125 nm 处引入一个虚拟原子,并将原本氧原子上的负电荷置于该虚拟原子上(该虚拟原子只含电量,不含质量),以改善水分子周围的静电分布,正电荷位置保持不变.水分子氢氧键长为0.09572 nm,键角为 104.52°,O 原子和 H 原子所带电荷分别为1.04ec和0.52ec,ec为单个电子所带的电荷.

本文采用12-6 Lennard-Jones (LJ) 势能模型应用于流体原子间及固-液原子间[19],其表达式为

式中,U为原子间的相互作用力,rij为原子间的距离,εij为原子间的势能参数,σij为原子间的尺寸参数,rc为截止距离.各原子之间的相互作用势能参数及作用距离如表2 所列[20].

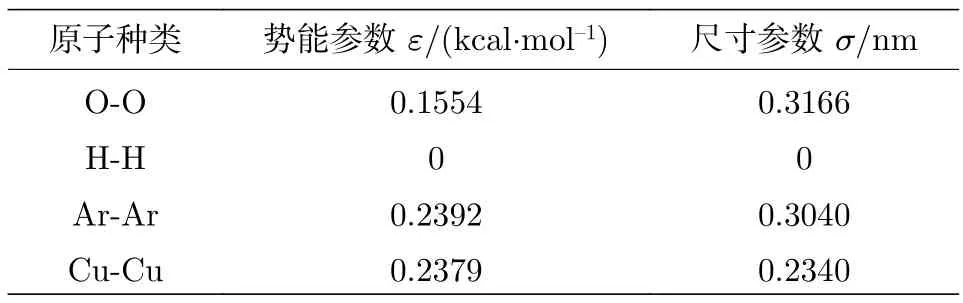
表2 各原子之间的相互作用势能参数及尺寸参数Table 2. Interaction potential energy parameters and size parameters of each atom.

对于其他原子间的势能参数εij与尺寸参数σij,采用Lorentz-Berthelot 混合方法进行计算[21]:

仿真系统的时间步长设置为1 fs,采用 Velocity-Verlet 算法对流体原子运动方程进行求解.为了使模拟计算的结果更加准确,在初始时刻,为每个分子设定随机的速度及位置.将整个系统在NVT 系综下进行弛豫,系统中的所有原子在280 K的温度下随机运动,计算50 万步(0.5 ns)以实现热力学平衡.然后撤消整个系统的NVT 系综,并将其设置为NVE 系综,加热层原子设置NVT 系综,对流体区域的水分子和氩原子在Y方向上施加一个外力F=0.0005 kcal/(mol·Å),继续运行50 万步(0.5 ns),然后重新开始计时并运行1000 万步(10 ns),并对整个系统进行区域划分,统计数据.本文中分子动力学模拟均采用LAMMPS 开源代码实现,系统可视化使用OVITO 可视化软件完成[22].

2.2 模拟方法验证

为了验证模型及参数设置的正确性,对纳米通道中水分子的流动传热特性进行验证.具体是采用了Xi等[18]的工作,构建了一个33 Å×124 Å×24 Å的水分子流动传热模型,如图2(a)所示.固体基底原子采用面心立方结构进行排列,晶格常数设置为4.086 Å,相互作用参数设置为εs=4.5608 kcal/mol和σs=0.2633 nm,热基底与冷基底的间距D=52 Å.系统在NVT 系综下达到平衡后,将热基底的温度设置为353 K,冷基底温度设置为293 K,并进行4 ns 的数据收集.模拟的水分子温度分布如图2(b)所示,将结果与Xi等[18]提供的研究数据进行对比,基于冷热源的60 K 温差尺度下,最大相对误差约为1.32%,因此,可认为本文构建的模型与算法准确可靠.

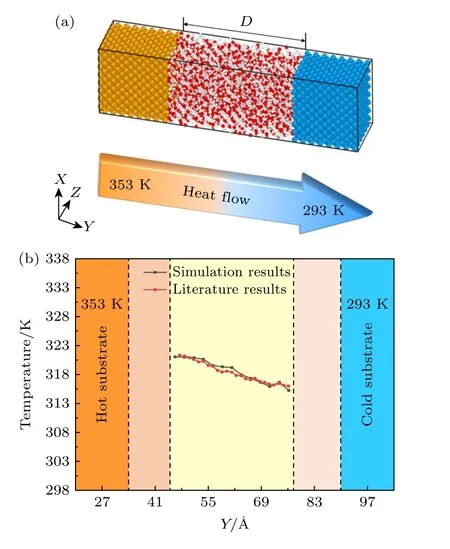
图2 水分子流动传热模拟验证(a) 模型示意图;(b) 温度分布Fig.2.Validation of water molecule flow heat transfer simulation: (a) Model Schematic;(b) temperature distribution.

3 结果与分析

3.1 不凝性气体对势能分布的影响

为了深入探究纳米通道内不凝性气体对流动传热的影响,首先计算了流体的势能分布.势能可以直观显示出原子在纳米通道中的排布情况,同时反映原子之间的相互作用能.流体在300,325,350 K 热源温度作用下的势能分布如图3 所示,Case 1 中不含不凝性气体,通道内水分子的势能分布相对均匀,而对于Case 2,Case 3,Case 4,Case 5,由于不凝性气体的存在,流体在流动的过程中,氩原子会形成团簇,并集中分布在纳米通道的中心区域,其表现为一个明显的高势能区域,Case 2 中氩原子含量最多,形成的团簇更大,高势能区域也更大.固-液界面处始终存在着低势能区域(深蓝色区域),使更多的流体原子被壁面捕获.在相同的热源温度下,Case 1 的低势能区相较于其余4 种情况更加显著,这意味着氩原子的存在削弱了固体壁面与水分子之间的相互作用力.当T0=300 K 时,流体的势能较低,氩原子形成的团簇更大;而随着热源温度的上升,流体的势能升高,氩原子团簇逐渐变小,并且热源温度达到350 K 时,Case 3,Case 4,Case 5 中的氩原子团簇基本消失,表明热源温度的升高可以显著增加原子运动的剧烈程度,使纳米通道中原子整体分布趋向均匀.

图3 流体的势能分布Fig.3.Potential energy distribution of a fluid.

数密度反映了通道内水分子和氩原子的分布情况,对流体的势能分布情况作出进一步的解释,分别统计了水分子和氩原子在纳米通道内的数密度分布,如图4 所示.图中,横坐标为纳米通道的Z方向,单位为Å,纵坐标为水分子数密度,单位为Å-3.水分子和氩原子的数密度在近壁面处均出现了明显的振荡现象,这意味着壁面附近流体的分层现象更加显著;壁面捕获了更多的水分子,从而形成了图3 中的低势能区.图4(a),(b)展示了300 K 热源温度下水分子和氩原子的分布情况,水分子在壁面附近存在高密度层,而氩原子更多地集中在了中心区域.Case 1 的情况下由于纳米流道中不存在氩原子,其中心区域数密度基本保持恒定;Case 2中水分子的数量最少,同时水的数密度最低;Case 3,Case 4,Case 5 水分子数密度在中心区域基本相同,而对于壁面处的高密度层,数密度峰值分别为0.0738,0.0743,0.0751,这意味着氩原子数量的增加可以削弱壁面对水分子的吸引力.图4(c),(e)分别对应热源温度T0=325,350 K 的情况.通过对比图4(a),(c),(e)可知,随着热源温度的上升,流体的分层现象被削弱,出现这种现象的原因是高温使纳米通道内分子运动更加剧烈,导致壁面吸附水分子的能力变弱,水分子有更大的可能性脱离壁面的束缚.图4(b),(d),(f)展现了不同温度下氩原子数密度的变化规律,随着热源温度的升高,氩原子在壁面附近的分层现象也随之减弱,整体的数密度分布更加均匀.

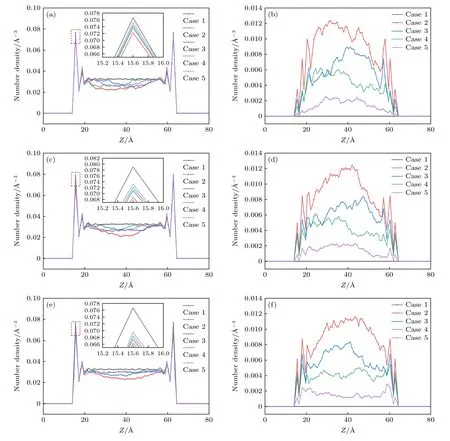
图4 流体的数密度分布(a) T0=300 K,H2O;(b) T0=300 K,Ar;(c) T0=325 K,H2O;(d) T0=325 K,Ar;(e) T0=350 K,H2O;(f) T0=350 K,ArFig.4.Number density distribution of fluids: (a) T0=300 K,H2O;(b) T0=300 K,Ar;(c) T0=325 K,H2O;(d) T0=325 K,Ar;(e) T0=350 K,H2O;(f) T0=350 K,Ar.

3.2 不凝性气体对流体速度的影响

纳米通道内流体的速度分布是研究流体流动特性的重要参数.当实际流体流过固体壁面时,沿着Y方向的速度可以通过的Navier-Stokes 方程来确定,其表达式为

其中,ρ(y,z) 是流体的质量密度,µ是流体的剪切黏度,uf,Y是沿Y方向流体的流动速度,是沿Y方向的压力梯度.在本模拟中,流速在Y方向上保持不变,因此,(5)式可以简化为[23]

图5 为5 种类流体在300,325,350 K 的热源温度下的速度分布.横坐标为Z方向,单位为Å,纵坐标为流体在Y方向的平均流速,单位为m/s,流体速度分布结果采用二次多项式函数进行拟合.纳米通道内流体的速度分布呈泊肃叶流动,中心的主流区域流速较高,近壁面区域由于受到固体壁面的约束导致流速较低.从图5(a)可以看出,Case 5 的情况下,流体的平均速度最高,超过了纯水情况下的Case 1,而氩原子含量最高的Case 2 平均流速最低.这意味着少量气体原子的存在可以削弱固体壁面对水分子高密度层的吸引力,从而起到促进流动的作用;而更多气体原子的出现导致中心区域形成更大的团簇,使纳米通道内流体的流动受到一定的阻碍.对比图5(a),(b),(c)可得,随着热源温度T0从300 K 升高至350 K,流体流动速度明显上升,这是因为温度的升高会致使分子运动更加剧烈,同时,固体壁面对流体的吸附能力也被削弱.图5(c)中,在T0=350 K 的情况下,Case 1 的速度有超过Case 5 的趋势,这表明了高温对固-液相互作用的削弱能力相较于不凝性气体而言更强,少量不凝性气体为流动带来的促进作用在高温下已经很小.

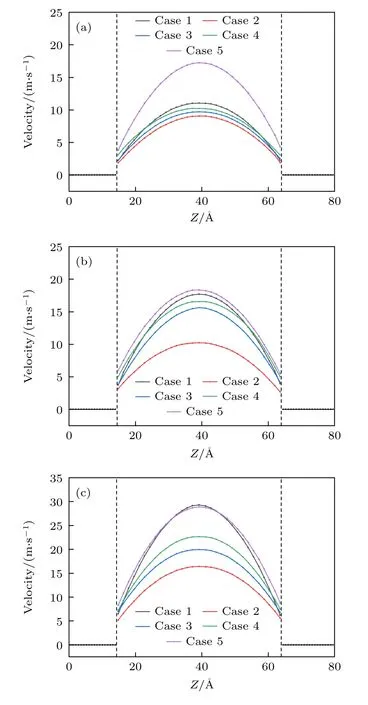
图5 流体的速度分布(a) T0=300 K;(b) T0=325 K;(c) T0=350 KFig.5.Velocity distribution of fluids: (a) T0=300 K;(b) T0=325 K;(c) T0=350 K.

图6 统计了纳米通道内流体边界区域的速度滑移.从图6 可以看出,流体的速度滑移始终为正滑移,且更高的热源温度会产生更大的速度滑移.Case 3,Case 4,Case 5 的速度滑移在T0=300,325,350 K 的情况下均大于Case 1,这种现象说明了不凝性气体对水分子高密度层有一定的吸引作用,从而减小了边界处的流动阻力;而Case 2 中更多的气体原子使得氩原子团簇结构对流体流动产生了阻碍作用,导致速度滑移更低.通过对比Case 2,Case 3,Case 4,Case 5 可以发现,在水中加入少量的气体原子可以削弱通道壁面的约束力,使得边界区域的速度滑移更大,而更多气体原子的加入会阻碍微通道内的流动.此外,在高温的情况下,纳米通道内的流体流动的速度滑移显著增大.

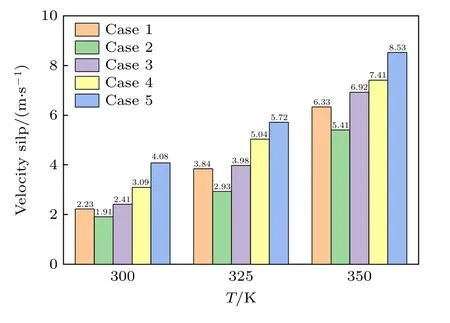
图6 流体的速度滑移Fig.6.Velocity slip of fluids.

计算了存在不凝性气体情况下流体的的流动阻力系数.流动阻力系数是影响流动的重要因素,从流动阻力的角度分析流动的影响是有说服力的.阻力系数f可定义为

其中,ρ是流体的质量密度,Δp表示沿着通道流动方向长度为LY的压降,um是通道横截面处的平均流体速度,Dh是水力直径.当水分子流过纳米通道时,由于在Y方向上对N个水分子中的每一个施加外力fY,使得流体被驱动.因此,fY的大小对应于Δp·A,在分子动力学模拟中可以推导出以下公式进行计算[24]:

根据(5)式,计算了上述各种情况下的阻力系数,如图7 所示.流动阻力系数f与平均流体速度的平方呈反比关系,这意味着阻力系数也会受热源温度的影响.当热源温度相同时,氩原子含量最高的Case 2 的阻力系数始终最大,而含有最少氩原子的Case 5 阻力系数最小,Case 3,Case 4 与纯水情况下的Case 1 阻力系数相差不大.随着热源温度T0从300 K 升高至350 K,5 种情况下的阻力系数均显著减小,这意味着高温能够有效降低微通道内的流动阻力.值得一提的是,当T0=350 K时,Case 1 的阻力系数减小至50.7,低于Case 4 情况下的65.5,且与Case 5 情况下的45.2 已经相差很小.这表明在高温的情况下,少量不凝性气体原子的存在对微通道内流体流动的促进作用受到削弱,而热源温度对流体阻力系数的影响则更加显著.

图7 流体的阻力系数Fig.7.Drag coefficient of fluids.

3.3 不凝性气体对流体传热的影响

为了探究不凝性气体对纳米通道内传热特性的影响,计算了5 种流体在热源温度T0分别为300,325,350 K 的情况下的温度分布.在分子动力学模拟中,流体的温度基于动力学输出,并通过如下公式得到[25]:

式中,vi为单个水分子的速度,为宏观流体的平均速度,KB为玻尔兹曼常数,为纳米通道中水分子的数量,m为水分子的质量.

纳米通道内流体的温度分布如图8 所示.图8(a)展示了300 K 热源温度下流体的温度云图.可以观察到,近壁面区域流体的温度略高于中心区域;Case 1 情况下流体的平均温度最高,温度分布也最为均匀;对于Case 2,Case 3,Case 4,Case 5 这4 种含有氩原子流体的情况,流体的平均温度比纯水更低,但在纳米团簇处会形成一个高温区域,这是因为团簇内部氩原子活动更加剧烈,平均分子动能更大.T0=325 K 的情况如图8(b)所示,随着热源温度的升高,氩原子形成的团簇更小,虽然流体的温度随之升高,但平均温度与热源温度之间的温差变大,意味着流体的传热能力受到影响.图8(c)展示了350 K 热源温度下流体温度分布情况,可以明显地看出,纳米团簇的减小或消失使得温度的分布更加均匀,且流体与壁面之间的温差更大,这一现象表明高温使得流体原子运动更加剧烈,同时传热能力产生恶化.

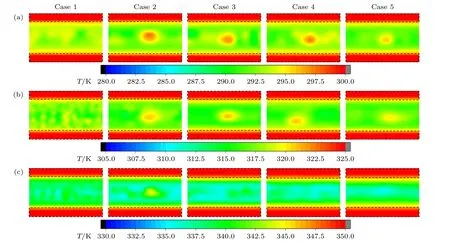
图8 流体的温度分布(a) T0=300 K;(b) T0=325 K;(c) T0=350 KFig.8.Temperature distribution of fluids: (a) T0=300 K;(b) T0=325 K;(c) T0=350 K.

水的氢键结构可以影响纳米通道内的传热作用[26],图9 展示了氢键结构的示意图.使用VMD软件对氢键数量进行了统计,氢键的判定依据是两个水分子的两个氧原子之间的距离小于3.5 Å,并且连接两个氧原子的矢量与氧和氢原子的矢量之间的角度小于35°.从热运动的角度看,氢键网络的形成可以更好地将一侧水分子的动能传递到另一侧,有利于流体的热传递.

图9 氢键示意图Fig.9.Hydrogen bonding schematic.

图10 展示了300 K 热源温度下纳米通道内的氢键数量.在模拟开始时,Case 1 的水分子数量最多,Case 2 水分子最少,而Case 3,Case 4,Case 5水分子数量相同,因此氢键数量也呈现出相同的规律.从图10(a)可以看出: 随着模拟过程的进行,纳米通道内流体的氢键数量逐渐收敛,流体的流动在3 ns 时趋于稳定;相较于Case 3 和Case 4,Case 5 收敛的数值最小,这是因为Case 5 内总原子含量更少,流动趋于稳定后,流体原子的平均间距更大,这不利于氢键的形成;另外,统计了Case 3在不同热源温度的情况下氢键数量的变化,如图10(a)插图所示,当热源温度上升时,流体的氢键数量明显减少,该现象表明高温会破坏水分子形成的氢键网络,这意味着热源温度T0升高时,虽然水分子吸收的总热量会增加,但它的传热能力也会受到一定的限制.图10(b) 统计了300 K 温度下流动稳定后平均单个水分子形成的氢键数量,Case 1中平均单个水分子形成的氢键数量最多,Case 2形成氢键最少,Case 3 与Case 4 略高于Case 5,这一现象表明纳米通道中水分子数量的增加能够提高平均单个水分子形成的氢键数量,而氩原子对氢键的影响幅度较小.

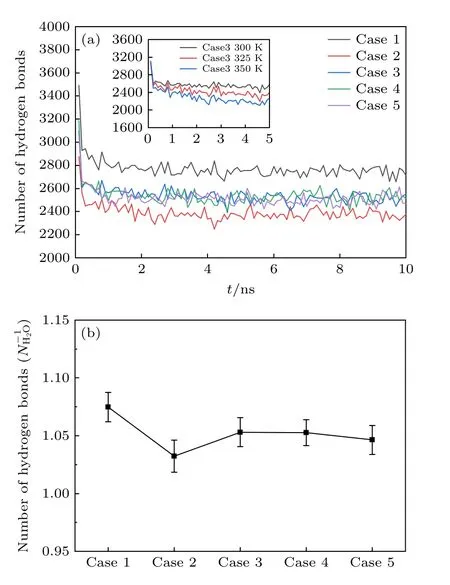
图10 流体的氢键数量(a)氢键数量;(b)平均单个水分子形成的氢键数量Fig.10.Number of hydrogen bonds in fluids: (a) Number of hydrogen bonds;(b) the average number of hydrogen bonds formed by a single water molecule.

为了探究纳米通道内的综合流动传热能力,计算了努塞尔数Nu,Nu是衡量对流换热强度的无量纲数.它表示流体底层的热传导阻力与对流热传递阻力之比.计算公式如下[27]:

其中hc是对流传热系数,Dh是特征尺寸,λ是流体的热导率.对流换热系数hc可由局部平均温度Tave计算:

其中,TW是壁面温度,Tave是沿Z方向的局部平均温度,是使用二次多项式函数拟合固体-液体界面处流体温度分布而获得的流体温度梯度.结合(9)式和(10)式可以得到:

式中,H是纳米通道的高度.

图11 显示了5 种情况下流体的努塞尔数(Nu).可以观察到,Nu受氩原子含量和热源温度影响,热源温度的升高会导致Nu小幅下降.Case 1 的情况下,更多的水分子形成了氢键网络,有利于强化流体的流动传热,因此Nu最大;Case 2 水分子相对较少致使Nu偏低;Case 3 相较于Case 4,Case 5,纳米通道内原子排列更加紧密,传热效果更好.值得一提的是,在T0=350 K 时,Case 2的Nu达到了3.51,超过了Case 5 的3.48,这意味着高温破坏了水分子的氢键网络,在这种情况下,Case 2 有更多的流体原子参与了传热,因此其努塞尔数更大.总的来说,氩原子的出现会对纳米通道内流体的流动传热产生一定的影响,但从整体上来看,Nu的变化幅度较小;高温的情况下,水分子形成的氢键网络受到影响,升高热源温度虽然可以使流体吸收的总热量增大,但会小幅降低流体的传热效率.

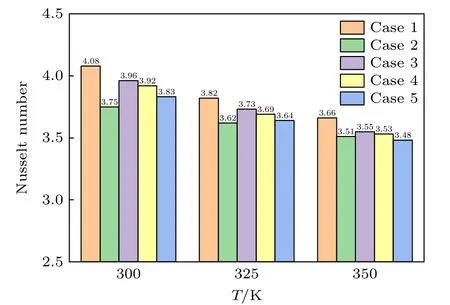
图11 流体的努塞尔数Fig.11.Nussle number of the fluid.

4 结论

本文采用分子动力学模拟的方法,研究了含有不凝性气体的水分子在纳米通道中的流动传热特性,探讨了在300,325,350 K 热源温度作用下氩原子对流体密度、速度和温度的影响,具体结论如下:

1) 流体在流动的过程中,不凝性气体氩原子易形成团簇居于流道的中心区域,并且具有较高的势能;固-液界面处存在低势能区域,并且氩原子的存在使低势能区域减小;热源温度的升高可以显著增加原子运动的剧烈程度,使纳米通道中流体平均势能升高;水分子和氩原子的数密度在近壁面处的分层现象变得显著,水分子在壁面处会出现高密度层,氩原子集中分布在中心区域;随着热源温度的上升,水分子数密度峰值降低,壁面吸附水分子的能力变弱,氩原子分层现象也随之减弱,原子整体分布趋向均匀.

2) 少量气体原子的存在可以促进流体的流动,而更多气体原子的出现会导致中心区域形成团簇,从而对流动产生阻碍作用;高温同样会使得纳米通道内的流体流动速度与速度滑移更大;阻力系数受氩原子含量和热源温度影响,氩原子含量最高的情况下阻力系数始终最大,而含有少量氩原子对流体的影响较小,随着热源温度升高,阻力系数显著减小.

3) 近壁面区域流体的温度略高于中心区域,但纳米团簇内部氩原子活动更加剧烈,平均分子动能更大,温度较高;随着温度的上升,纳米通道内流体的势能升高,氩原子形成的团簇逐渐变小或消失.水的氢键结构可以影响纳米通道内的传热,随着模拟进行,纳米通道内流体的氢键数量逐渐收敛,流动趋于稳定;氩原子会对氢键数量和流动传热产生影响,但从整体上来看,努塞尔数的变化幅度较小;当热源温度上升时,流体的氢键数量明显减少,这意味着高温会破坏水分子形成的氢键网络,流体的努塞尔数下降,从而导致流体的传热效率受到负面影响.