镱原子超精细诱导5d6s3D1,3→6s21S0 E2 跃迁及超精细常数的精确计算*

赵国栋 曹进 梁婷 冯敏 卢本全 常宏‡

1) (中国科学院国家授时中心,西安 710600)

2) (时间基准及应用重点实验室,西安 710600)

3) (中国科学院大学天文与空间科学学院,北京 101408)

4) (合肥国家实验室,合肥 230026)

在镱原子中,利用5d6s3D1 →6s21S0 跃迁探索宇称破缺效应已经得到了深入的研究.但是5d6s3D1 态与基态6s21S0 之间的M1 跃迁和超精细诱导E2 跃迁很大程度上影响了宇称破缺信号的探测.因此,很有必要精确计算5d6s3D1 态与基态6s21S0 之间的M1 跃迁和超精细诱导E2 跃迁的跃迁概率.本文利用多组态Dirac-Hartree-Fock 理论精确计算了5d6s3D1 →6s21S0 M1 跃迁和超精细诱导5d6s3D1,3 →6s21S0 E2 跃迁的跃迁概率.计算时详细分析了电子关联效应对跃迁概率的影响.此外,还分析了不同微扰态和不同超精细相互作用对跃迁概率的影响.本文计算的3D1,2,3和1D2 态的超精细常数与实验测量结果符合得很好,从而证明了本文所用计算模型的合理性.结合实验测量的超精细常数和本文理论计算所得的核外电子在原子核处的电场梯度,重新评估了173 Yb 原子核电四极矩 Q=2.89(5)b,评估结果与目前被推荐的结果符合得很好.

1 引言

弱相互作用力是迄今为止唯一已知违反空间反演对称性(宇称)的基本相互作用力[1].这种宇称破缺(parity violation,PV)效应可以用来分离出原子系统中的弱相互作用,为检验标准模型提供了一种新的方法[2,3].宇称破缺效应在镱原子5d6s3D1→6s21S0跃迁中得到了广泛研究[4,5],最新实验[6]的精度达到了0.5%,在此精度下不仅能够探测镱原子的PV 振幅随同位素的变化,从而获得附加Z 玻色子与电子、质子和中子相互作用的极限,而且可以观察到与核自旋相关的PV 振幅,其大小比与核自旋无关的宇称破缺振幅小两个数量级.

对于实验观测到的镱原子5d6s3D1→6s21S0跃迁中宇称破缺信号,最大的贡献来自PV 振幅与Stark 诱导跃迁振幅的干涉项[7,8],其他较小的贡献则来自M1 禁戒跃迁和超精细诱导E2 跃迁与PV 振幅的干涉.因此,精确计算5d6s3D1→6s21S0M1 跃迁和超精细诱导5d6s3D1→6s21S0E2 跃迁的跃迁概率对于解释3D1→1S0跃迁的宇称破缺信号具有重要的研究意义.调研发现,Stalnaker等[9]以及Sur 和Chaudhuri[10]分别对5d6s3D1→6s21S0M1 禁戒跃迁的跃迁概率进行了测量和计算.而对于超精细诱导5d6s3D1→6s21S0E2 跃迁,仅有Kozlov等[11]考虑了超精细诱导下3D1和3D2态之间的混合,并利用组态相互作用结合多体微扰理论(configuration interaction combined many-body perturbation theory,CI+MBPT)方法计算了超精细诱导禁戒跃迁的跃迁概率.他们的结果不仅忽略了1D2态与3D1态的超精细诱导态混合对跃迁概率的影响,而且超精细常数的计算结果与实验值之间存在3%—26%的差距.因此,我们认为有必要利用不同的理论重新计算超精细诱导禁戒跃迁的跃迁概率.

本文采用多组态Dirac-Hartree-Fock (multiconfiguration Dirac-Hartree-Fock,MCDHF)方法重新计算了171,173Yb原子中5d6s3D1→6s21S0M1跃迁和超精细诱导5d6s3D1,3→6s21S0E2 跃迁的跃迁概率以及5d6s3D1,2,3,1D2态的超精细常数.计算诱导跃迁概率时同时考虑了5d6s3D2态和5d6s1D2态与5d6s3D1,3态的超精细诱导态混合,并给出了171,173Yb原子中5d6s3D1,3→6s21S0E2 跃迁的跃迁概率.此外,我们计算的3D1,2,3和1D2态的超精细常数与实验测量结果符合得很好.结合实验上测量的电四极超精细常数B和理论上计算的核外电子在原子核处的电场梯度,重新评估了173Yb原子核电四极矩Q=2.89(5)b,与目前173Yb原子核电四极矩的推荐结果[12]符合得很好.

2 理论计算

2.1 超精细相互作用

由于171Yb和173Yb 原子核内的质子和中子都存在轨道运动与自旋,其矢量和产生的电磁多极矩将会与原子核外电子发生超精细相互作用,使原子核自旋I与电子的总角动量J发生耦合,并产生新的总角动量F=I+J.超精细相互作用的哈密顿量Hhfs可用一系列张量算符展开[13]:

式中T(k)与M(k) 分别表示作用于电子坐标空间和原子核坐标空间上的k阶球张量算符,k=1 表示磁偶极相互作用,k=2 表示电四极相互作用,由于超精细作用高阶效应影响较小,这里忽略k ＞2的部分.根据Racah[14]提出的理论,超精细相互作用矩阵元可写为

式中M表示磁量子数,γ表示用来区分量子态的其他量子数.在相对论框架下,电子部分的球张量算符可表示为[15]

其中α 为精细结构常数,α为狄拉克矩阵,C(k) 为球谐张量算符,求和指标j表示第j个电子,rj为第j个电子的位移矢量.而对于原子核部分的约化矩阵元[15]:

其中µI与Q分别为原子核磁偶极矩和电四极矩.

根据超精细相互作用矩阵的对角元(J=J′),可以定义磁偶极超精细常数A和电四极超精细常数B为[16]

根据(7)式,核电四极矩可由下式计算[17-19]:

Q单位为b,其中

为原子核附近核外电子的电场梯度(electric field gradient,EFG),(8)式中超精细相互作用常数B和EFG 分别以MHz 和a.u.为单位.

2.2 超精细诱导跃迁

可以将初态|γ′IJ′F′M′〉与末态|γIJFM〉 之间电四极E2 跃迁的跃迁概率表示为[20,21]:

其中λ 为跃迁上下能级差对应的波长.对同一精细结构内的所有超精细低能级求和后的跃迁概率为[22]

在超精细相互作用下,相同宇称和总角动量量子数F的原子态间将发生混合,一定程度上打开了原本完全禁戒的跃迁,这种跃迁称为超精细诱导跃迁[23-26].本文令超精细混合后的跃迁初态为末态为式中的波浪号表示波函数的主要分量.根据一阶微扰理论,此时初态可展开为

εn为微扰态;展开系数为混合系数,

原子末态可用同样的方法展开,

利用矩阵元约化公式[27]以及Wigner-Eckart 定理,可将跃迁矩阵元约化为

将约化后的跃迁矩阵元代入(11)式,可得出超精细诱导跃迁概率的表达式:

2.2.1 镱原子超精细诱导5d6s3D1IF′→6s21S0E2 跃迁

对于5d6s3D1IF′→6s21S0跃迁,利用(12)式可将初态5d6s3D1IF′M′表示为

对于5d6s3D1激发态,仅考虑同一组态中3D2,1D2态与3D1态的混合.其他不同组态的相互作用可以忽略不计,因为它们之间的能级差太大并且超精细相互作用很弱.末态6s21S0为基态,由于镱原子基态与其他能级间的能级差太大,导致相应的混合强度很弱,因此基态与其他能级间的混合可忽略不计.所以末态的波函数可表示为

此时超精细诱导E2 跃迁的跃迁矩阵元等于

由(19)式可知诱导跃迁概率

2.2.2 镱原子超精细诱导5d6s3D3IF′→6s21S0E2 跃迁

镱原子跃迁初态5d6s3D3IF′M′在超精细相互作用下可展开为

与5d6s3D1IF′M′类似,仅考虑同一组态中3D2,1D2态与3D3态之间的混合.此时跃迁矩阵元等于

代入(19)式后可得如下跃迁概率公式:

2.3 多组态Dirac-Hartree-Fock 理论

在多组态Dirac-Hartree-Fock 方法[28-30]中,原子态波函数Ψ(ΓPJMJ) 由一组具有相同的宇称P、总角动量J以及磁量子数MJ的组态波函数Φ(γPJMJ)的线性组合来表示,即

其中cj为组态混合系数,Γ与γ表示除P,J,MJ外区分量子态的其他量子数.组态波函数由相对论单电子自旋轨道波函数的乘积线性组合而成.单电子狄拉克轨道具有以下形式:

式中P(r)与Q(r) 为单电子狄拉克轨道的径向部分,χκm(θ,φ)与χ-κm(θ,φ) 为角向部分.自洽场(self-consistent field,SCF)中通过求解多参考组态方程,组态混合系数cj和单电子狄拉克轨道的径向部分被同时优化.在相对论组态相互作用(relativistic configuration interaction,RCI)中,仅有组态混合系数被优化.在组态相互作用中可以考虑[28]高阶电子关联效应、Breit 相互作用和量子电动力学(quantum electrodynamics,QED)修正.获得原子态波函数后,跃迁概率可通过约化矩阵元〈γJ‖Oλ‖γ′J′〉 来计算,其中Oλ为电磁场多极算符.

3 计算模型

电子关联效应是指量子态实际的能量与Hartree-Fock 近似下所得的能量间的差异.对于多电子原子体系,Dirac-Hartree-Fock 近似不足以准确描述原子的结构和性质,原因在于电子关联效应对多电子原子体系的影响较大.计算时我们采用活动空间方法[30,31]系统评估电子关联效应.由微扰论可知,电子关联效应分为一阶关联和高阶关联.一阶关联进一步分为价电子间的关联(valence-valence,VV),价电子与壳层电子间的关联(corevalence,CV)以及壳层电子之间的关联(corecore,CC) 三种.通过单参考组态单激发(single excitation)或双激发(double excitation)至活动空间形成的组态空间来描述一阶关联.待一阶关联描述充分后,挑选组态空间中混合系数较大的组态加入多参考组态(multi-reference,MR)基组,利用MR 基组单双激发产生的组态空间来描述高阶电子关联效应[19].由于从MR 基组单双激发等价于从单参考组态三四激发[32],MR 方法在很大程度上节约了计算资源,提高了计算效率.

计算时将基态6s2和激发态5d6s 同时优化.首先,在Dirac-Hartree-Fock (DHF)近似中,优化了参考组态{4s24p64d104f145s25p65d6s;4s24p64d104f145s25p66s2}中的光谱轨道.参考组态中最外层 5d 和6s轨道上的电子被当成价电子,其他的电子为壳层电子.随后在自洽场中,考虑了价电子与价电子及n≥3壳层电子与价电子之间的关联效应.组态空间的扩展是通过从参考组态限制性单双激发产生组态波函数的形式实现的.限制性单双激发代表最多只有一个电子从壳层电子激发,其他的来自于价电子的激发.在本文的计算中,占据的壳层逐层打开以激发至虚轨道,即先打开 5sp 壳层,随后打开4spd 壳层.同时,虚轨道也是通过一层层扩展的,并且每次只优化新加入的虚轨道.为了充分考虑VV 和CV 关联,扩展了七层虚轨道以确保计算的物理量的收敛性.计算中,每一步的计算模型被标记为CnV-m,其中n代表最新打开的壳层,m代表添加的虚轨道层数.为了提高计算效率,去除了与参考组态无相互作用的组态[33].在C4V-7 计算模型中获得的轨道基被用于随后的RCI 计算.

随后,在RCI 中考虑了n=5 壳层间的CC关联.为了充分考虑这部分的CC 关联效应,七层虚轨道被激发以实现组态空间的继续扩展.相应的计算模型被标记为CC5-7.此外,通过多参考组态单双激发的方法[32]来考虑n≥5 电子的高阶关联效应.多参考组态是通过在CC5-7 的组态空间中挑选出重要的组态形成的,即组态混合系数大于等于0.05 的组态.计算中挑选出的多参考组态为{5s25p66p2;5s25p65d2;5s25p46s26d7d;5s25p66s7s;5s25p45d6s26d;5s25p55d6s6p;5s25p65f6p;5s25p66s6d;5s25p66d7s}.为了实现组态空间的继续扩展,从多参考组态的单双激发至前三层虚轨道产生的组态被加入进来,相应的计算模型被标记为MR-3.最后,基于MR-3 模型,Breit 相互作用和QED 效应的影响被评估.不同计算模型下的组态个数如表1所列,并利用GRASP2018 程序包[34]完成计算.此外,利用rhfszeeman 程序[23]计算非对角超精细相互作用矩阵元,用transition-phase 程序[23]计算电四极跃迁矩阵元.

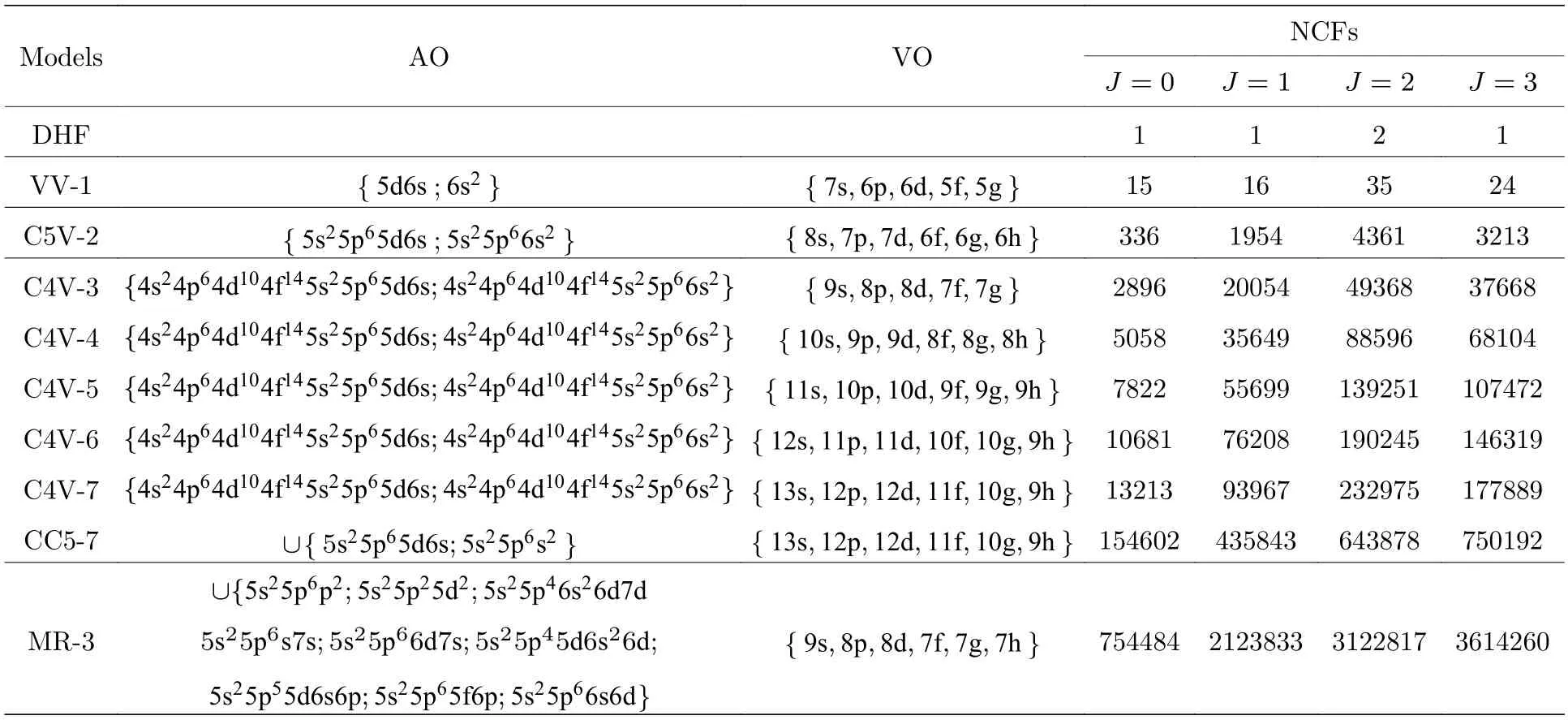
表1 不同计算模型下打开的光谱轨道(active orbitals,AO)、虚轨道(virtual orbitals,VO) 以及模型产生的组态空间内总的组态个数(number of configuration state wavefunctions,NCFs). J=0 表示1S0 态,J=1,3表示3D1,3 态,而J=2对应3D2和1D2态Table 1. Active orbitals (AO),virtual orbitals (VO) opened under different calculation models,and NCFs is the total number of the configurations in the configuration space. J=0 represents1S0 state,J=1,3 represents3D1,3 states,and the J=2 corresponds to the3D2 and1D2 states,respectively.

4 计算结果及讨论

4.1 5d6s3D1→6s21S0 M1 跃迁及5d6s1,3D2→ 6s21S0 E2 跃迁

如图1 所示,本文计算并比较了不同虚轨道层数对应的5d6s3D1→6s21S0的M1 跃迁概率和5d6s1,3D2→6s21S0E2 跃迁概率.由图1 可知虚轨道添加至第七层后,3D1→1S0以及1,3D2→1S0跃迁概率的计算结果均达到收敛.

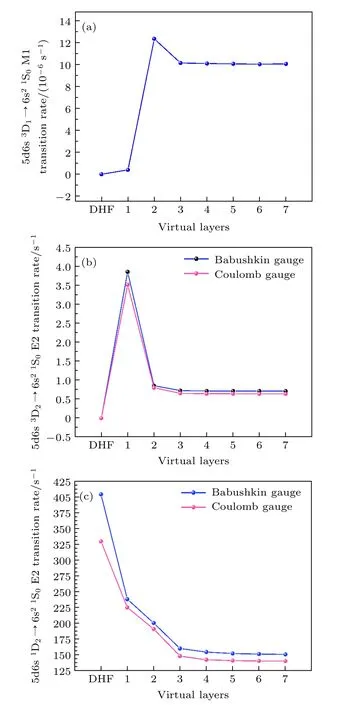
图1 5d6s3D1 →6s21S0 M1 跃迁及5d6s1,3D2 →6s21S0 E2 跃迁的跃迁概率随虚轨道扩展的变化Fig.1.Transition rates for 5d6s3D1 →6s21S0 M1 transition and 5d6s1,3D2 →6s21S0 E2 transition as a function of virtual orbital expansion.

表2 列出了不同模型下5d6s3D1→6s21S0M1 跃迁激发能ΔE、约化跃迁矩阵元(reduced matrix element,RME)和跃迁概率R的计算结果.由表2 可知VV 和CV 关联是影响3D1→1S0M1 跃迁参数的主要因素,它们使跃迁能和约化矩阵元分别变化了5.13%和98.8% .CC 关联对M1跃迁也存在较大影响.激发能和约化矩阵元在它们影响下的变化量分别为3.43% 与38.79% .此外,高阶电子关联效应和CC 关联之间存在一定程度的抵消效应.M1 跃迁激发能的计算结果与NIST数据库[35]给出的推荐值接近,二者相差0.24% .最后,在考虑了Breit 相互作用和QED 效应后,激发能和约化矩阵元的变化量分别为0.53% 和1.37% .本文约化矩阵元的计算结果处在文献[9]给出的测量误差范围以内.

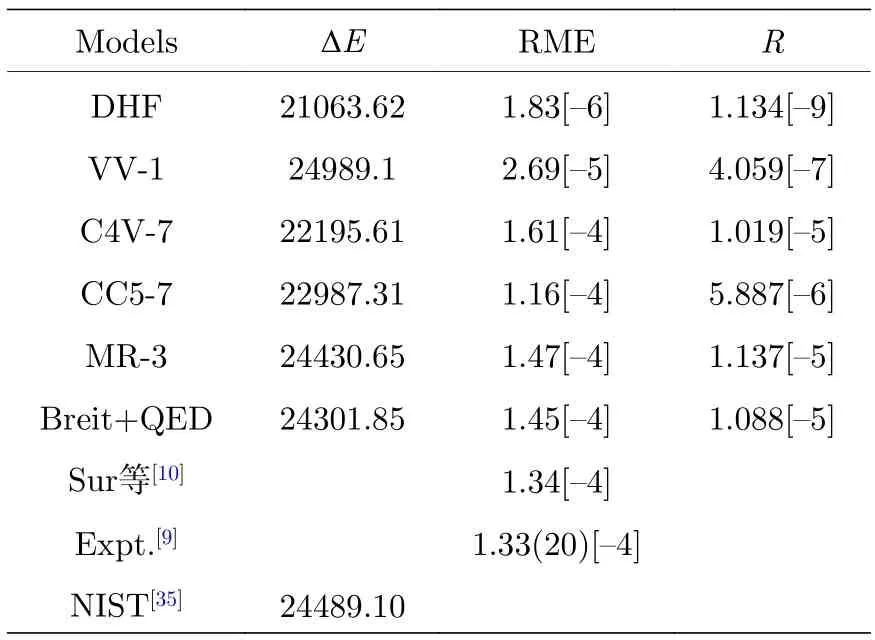
表2 不同计算模型下5d6s3D1 →6s21S0 M1 跃迁的激发能ΔE (cm-1),RME (a.u.)和跃迁概率R(s-1).方括号中的值表示以10 为底的指数,圆括号内的值表示误差Table 2. Excitation energyΔE(in cm-1),transition probability R (in s-1),and RME (in a.u.) for the 5d6s3D1 →6s21S0 M1 transition under various computational models.The values in brackets represent exponents with a base of 10,and values in parentheses indicate errors.

表3 列出了不同模型下计算的5d6s1,3D2→6s21S0E2 跃迁的激发能ΔE,RME 和跃迁速率R.表中V 表示速度规范,L 表示长度规范.理论上不同规范下的跃迁矩阵元应给出同样的跃迁线强和跃迁速率的计算结果,但采用MCDHF 方法得到的原子态波函数为实际原子态波函数的近似,从而造成两种规范下的计算结果有一定差别.由表3可知,VV 和CV 关联对5d6s3D2→6s21S0E2 跃迁的跃迁能和跃迁概率的影响分别为5.1% 和100% .在高阶电子关联效应的影响下,3D2与1D2至1S0E2 跃迁的激发能接近于NIST 的推荐值,与其分别相差0.26% 和2.99% .

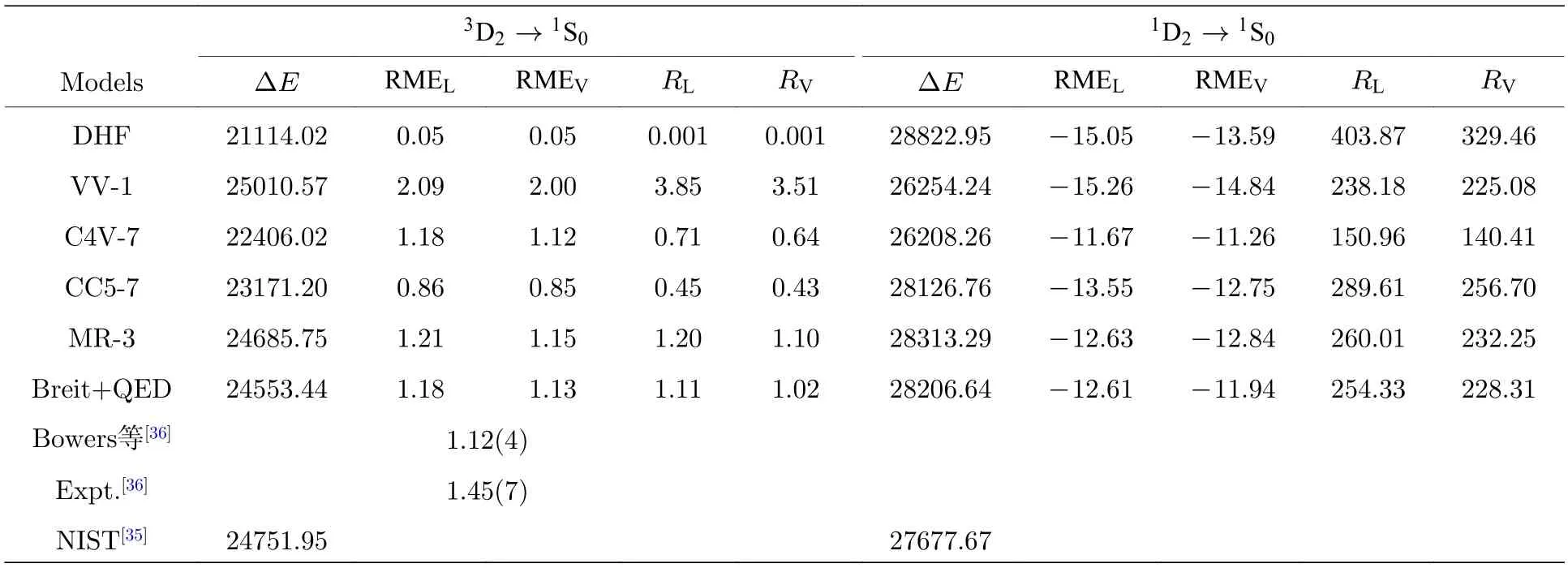
表3 5d6s1,3D2 →6s21S0 E2 跃迁的激发能ΔE (cm-1 ),RME(a.u.) 和跃迁概率R(s-1)在不同计算模型下的结果.V 表示速度规范,L 表示长度规范Table 3. Excitation energyΔE(in cm-1 ),RME (in a.u.),and transition probability R (in s-1) for the 5d6s1,3D2 →6s21S0E2 transition under various computational models.“V” denotes the velocity gauge,and “L” represents the length gauge.

4.2 5d6s3D1,2,3,1D2 态超精细常数与173Yb核电四极矩

表4 列出了171Yb及其同位素173Yb 的磁偶极超精细常数A与电四极超精细常数B的计算结果,并与以往的理论计算和实验测量结果进行了比较.表中Expt.与Theory 分别表示实验测量值与理论计算值.与其他理论的计算结果相比,本文采用MCDHF 方法计算的171,173Yb原子5d6s3D1,2,3态磁偶极和电四极超精细常数更接近实验值[36-39].例如173Yb 的5d6s3D1态,本文计算所得的超精细常数A,B与实验值分别相差3.73% 和0.43%,而文献[11,40]中利用CI+MBPT 理论计算的A和B与实验测量结果的差距大于5%和13% .对于5d6s3D2态,本文计算的A和B与实验值的差距小于1%,文献[40]结果与实验值分别相差3.41%和9.65%,文献[11]结果与实验值分别相差2.6%和20.5% .在文献[40]的计算中,仅考虑了VV 与CV 关联,而在本文的计算中,不仅考虑了VV 与CV 关联,还考虑了CC 和高阶关联效应.对于5d6s1D2态超精细常数B,本文计算结果比文献[40]的结果稍差,但仍处在实验测量结果[39]的误差范围内.

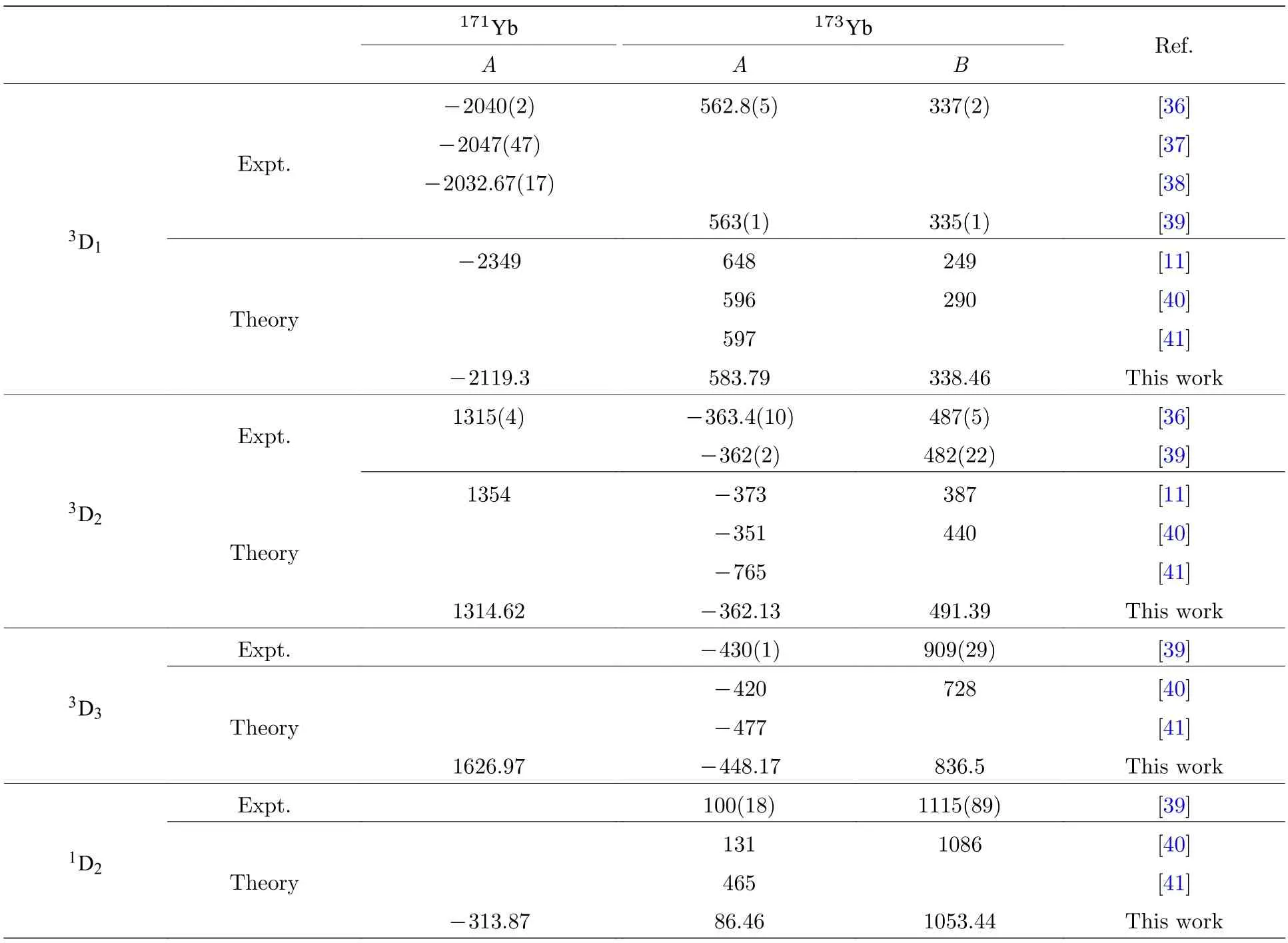
表4 5d6s3D1,2,3 态与1D2 态的磁偶极超精细常数A (MHz)和电四极超精细常数B (MHz)Table 4. Magnetic dipole hyperfine constant A (in MHz) and electric quadrupole hyperfine constant B (in MHz) for the 5d6s3D1,2,3 and1D2 states.

表5 列出了不同模型下173Yb原子5d6s3D1,2,3态的EFG 值.结合实验测量的电四极超精细常数B,重新评估了173Yb 原子核电四极矩.根据MR-3模型的计算结果,5d6s3D1,2,3态下本文评估的核电四极矩分别为Q(3D1)=2.79 b,Q(3D2)=2.77 b,Q(3D3)=3.04 b.取它们的平均为最终的评估结果Q=2.89 b,统计误差为0.02 b.将5d6s1D2态排除在外,因为它的超精细常数对电子关联效应特别敏感.由于壳层电子与壳层电子之间的关联与对应的高阶关联效应存在部分抵消现象[42,43],将n=4 的CC 关联效应对EFG 的影响作为剩余电子关联效应引起的误差.取以上两种方法中最大的误差为最终误差.因此,本文评估的173Yb 原子核电四极矩为Q(173Yb)=2.89(5)b .

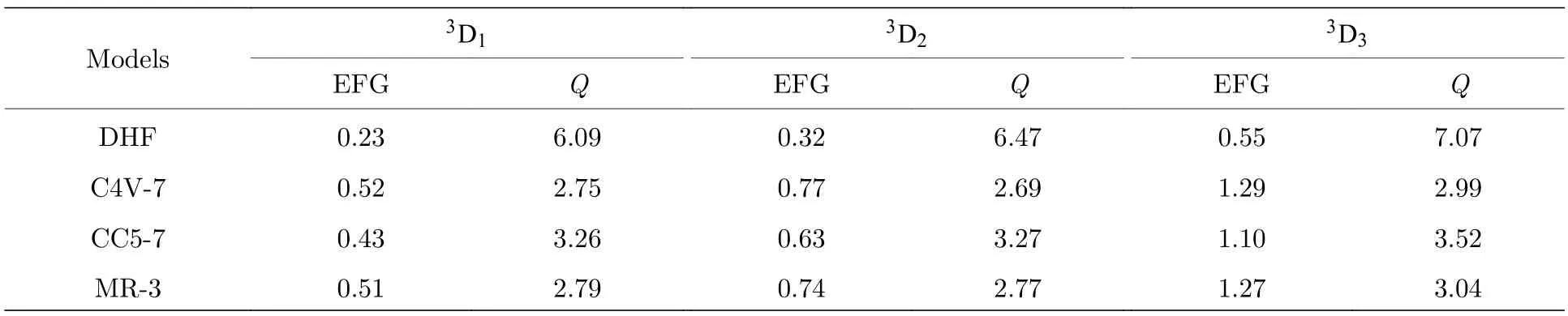
表5 不同模型下的EFG(a.u.),以及重新评估后的173 Yb 原子核电四极矩Q(b)Table 5. The EFG (in a.u.) calculated under different models,along with the reassessment of the nuclear electric quadrupole moment Q (in b) for173 Yb.

Holmgren[41]利用相对论自洽场方法计算了173Yb原子6s5d3D1,2,3,1D2和6s6p3P1,2,1P1态的波函数,并结合实验测量的超精细常数B,评估的173Yb原子核电四极矩Q=3.6 b .此外,Singh等[44]测量了173Yb原子3P2态的电四极超精细常数B,并结合他们利用相对论耦合簇(relativistic coupled-cluster,RCC)方法计算的核外电子在原子核处的电场梯度,评估173Yb原子核电四极矩为Q=2.46(12)b.目前,173Yb 核电四极矩的推荐值Q(173Yb)=2.80(4)b是通过测量μ镱原子X射线和原子核γ射线得到的[45],本文计算所得的结果与其符合得很好.与Holmgren 以及Singh 等评估的结果相比,本文的结果更接近于173Yb 原子核电四极矩的推荐值,同时评估误差更小.

4.3 171Yb和173Yb 超精细诱导5d6s3D1,3IF'→ 6s21S0E2 跃迁

表6 列出了171Yb和173Yb 原子中超精细诱导5d6s3D1,3→6s21S0E2 跃迁的混合系数.计算混合系数时核磁偶极矩、核电四极矩、矩阵元以及能级差均采用原子单位[46].原子单位下核磁矩µI(a.u.)=µN×µI(nm),µN=1.987131×10-6,核电四极矩Q(a.u.)=3.5706×10-8×Q(b) .对于171Yb,µI=0.49367(1)nm,Q=0.而对于173Yb,µI=-0.67989(3)nm,Q=2.8 b .

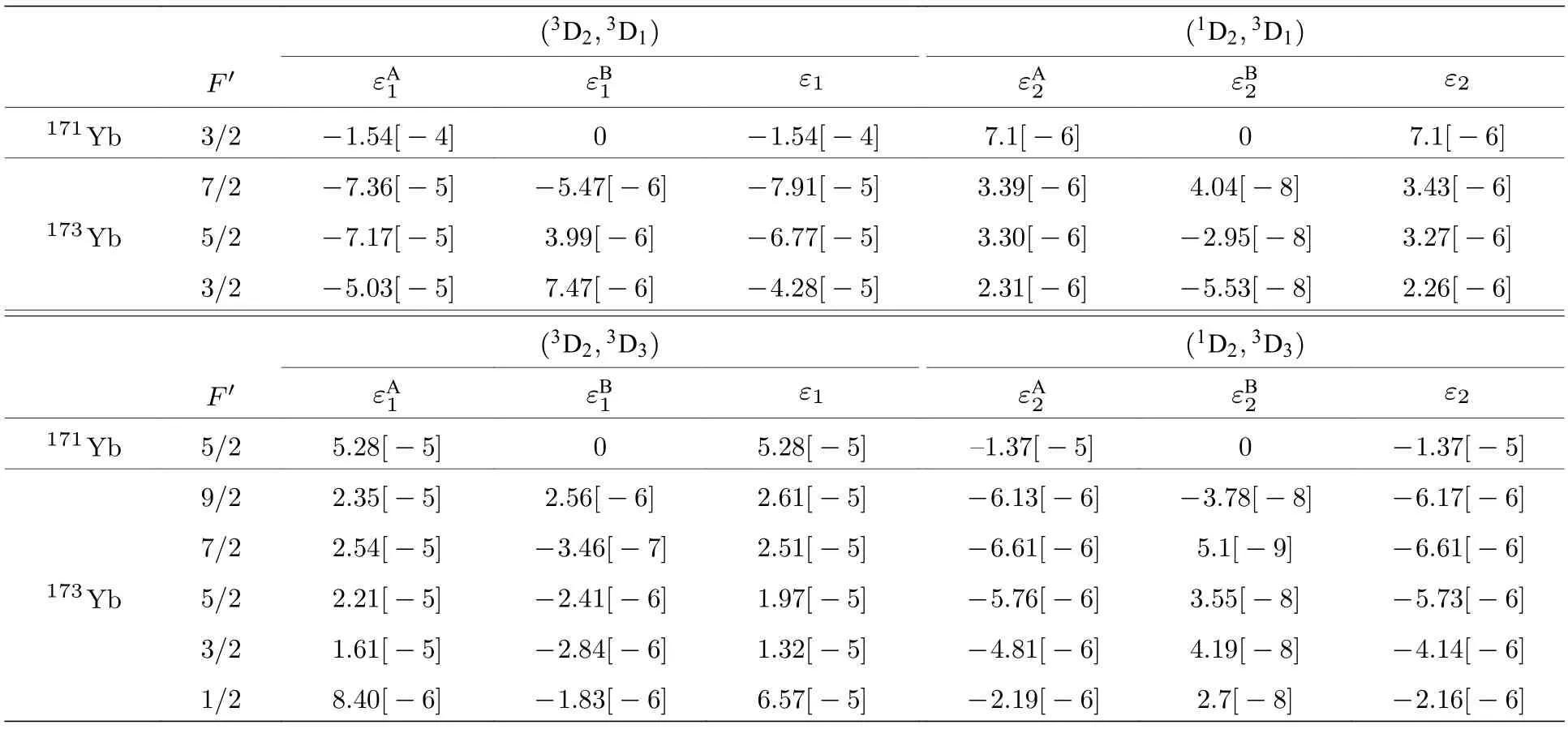
表6 171Yb和173Yb原子的超精细诱导5d6s3D1,3IF′ →6s21S0 E2 跃迁的混合系数(a.u.)Table 6. Mixing coefficients (in a.u.) for the hyperfine-induced 5d6s3D1,3IF′ →6s21S0 E2 transition in171Yb and173Yb.

将表3 中5d6s1,3D2→6s21S0E2 跃迁的跃迁矩阵元以及表6 所列的混合系数代入(23)式与(26)式,即可得到171Yb和173Yb 的超精细诱导5d6s3D1,3IF′→6s21S0跃迁的跃迁概率.计算并统计了不同微扰态和不同超精细相互作用对超精细诱导E2 跃迁的跃迁概率的贡献.如表7 所列,磁偶极超精细相互作用对跃迁概率的贡献比电四极超精细相互作用的贡献高2—3 个数量级,因此在超精细诱导跃迁中磁偶极超精细作用导致的态混合始终为主要部分.超精细诱导5d6s3D1IF′→6s21S0E2 跃迁在磁偶极超精细作用下,3D2微扰态与1D2微扰态对应的跃迁概率都随着总角动量量子数F的减小而减小,但同一F下3D2态的贡献始终是1D2态的3 倍以上;在电四极超精细作用下,3D2态的贡献比1D2态高1—2 个数量级.对于超精细诱导5d6s3D3IF′→6s21S0E2 跃迁,磁偶极超精细作用下1D2微扰态的贡献始终大于3D2微扰态的贡献.最终计算并总结了不同总角动量量子数F′对应的超精细诱导5d6s3D1,3IF′→6s21S0E2 跃迁的跃迁概率.相应的计算结果统计于表7 的Total 列.

表7 171Yb和173Yb的超精细诱导5d6s3D1,3IF′ →6s21S0 E2 跃迁的跃迁概率(s-1 ). T1与T2 分别表示磁偶极超精细相互作用与电四极超精细相互作用下的诱导跃迁概率. R1与R3 表示超精细诱导跃迁5d6s3D1IF′ →6s21S0中3D2 微扰态和1D2 微扰态与3D1 态混合后的诱导跃迁概率.与表示超精细诱导跃迁5d6s3D3IF′ →6s21S0中3D2微扰态和1D2 微扰态与3D3 态混合后的诱导跃迁概率.方括号内的数值代表以10 为底的指数,圆括号内的数值代表误差Table 7. Transition probabilities (in s-1 ) for the hyperfine-induced 5d6s3D1,3IF′ →6s21S0 E2 transitions in171Yb and173Yb .T1 and T2 represent the induced transition probabilities under magnetic dipole hyperfine interaction and electric quadrupole hyperfine interaction,respectively. R1 and R3 represent the transition probabilities in the hyperfine-induced transition 5d6s3D1IF′ →6s21S0,where the perturbed states3D2 and1D2 are mixed with the3D1 state.Similarly, and denote the transition probabilities in the hyperfine-induced transition 5d6s3D3IF′ →6s21S0,where the perturbed states3D2 and1D2 are mixed with the3D3 state.The numerical values in square brackets denote the exponentiation with base 10,while the values in parentheses represent the error.

表7 171Yb和173Yb的超精细诱导5d6s3D1,3IF′ →6s21S0 E2 跃迁的跃迁概率(s-1 ). T1与T2 分别表示磁偶极超精细相互作用与电四极超精细相互作用下的诱导跃迁概率. R1与R3 表示超精细诱导跃迁5d6s3D1IF′ →6s21S0中3D2 微扰态和1D2 微扰态与3D1 态混合后的诱导跃迁概率.与表示超精细诱导跃迁5d6s3D3IF′ →6s21S0中3D2微扰态和1D2 微扰态与3D3 态混合后的诱导跃迁概率.方括号内的数值代表以10 为底的指数,圆括号内的数值代表误差Table 7. Transition probabilities (in s-1 ) for the hyperfine-induced 5d6s3D1,3IF′ →6s21S0 E2 transitions in171Yb and173Yb .T1 and T2 represent the induced transition probabilities under magnetic dipole hyperfine interaction and electric quadrupole hyperfine interaction,respectively. R1 and R3 represent the transition probabilities in the hyperfine-induced transition 5d6s3D1IF′ →6s21S0,where the perturbed states3D2 and1D2 are mixed with the3D1 state.Similarly, and denote the transition probabilities in the hyperfine-induced transition 5d6s3D3IF′ →6s21S0,where the perturbed states3D2 and1D2 are mixed with the3D3 state.The numerical values in square brackets denote the exponentiation with base 10,while the values in parentheses represent the error.

表8 列出了本文与其他理论计算的超精细诱导 5d6s3D1→6s21S0跃迁振幅的计算结果的比较.跃迁振幅正比于混合系数与约化跃迁矩阵元的乘积,通过比较发现,本文计算得到的跃迁振幅与Kozlov等[11]的结果存在差异的主要原因是混合系数不同.由于混合系数与超精细相互作用非对角元相关,而本文计算的超精细常数更接近于实验测量结果.

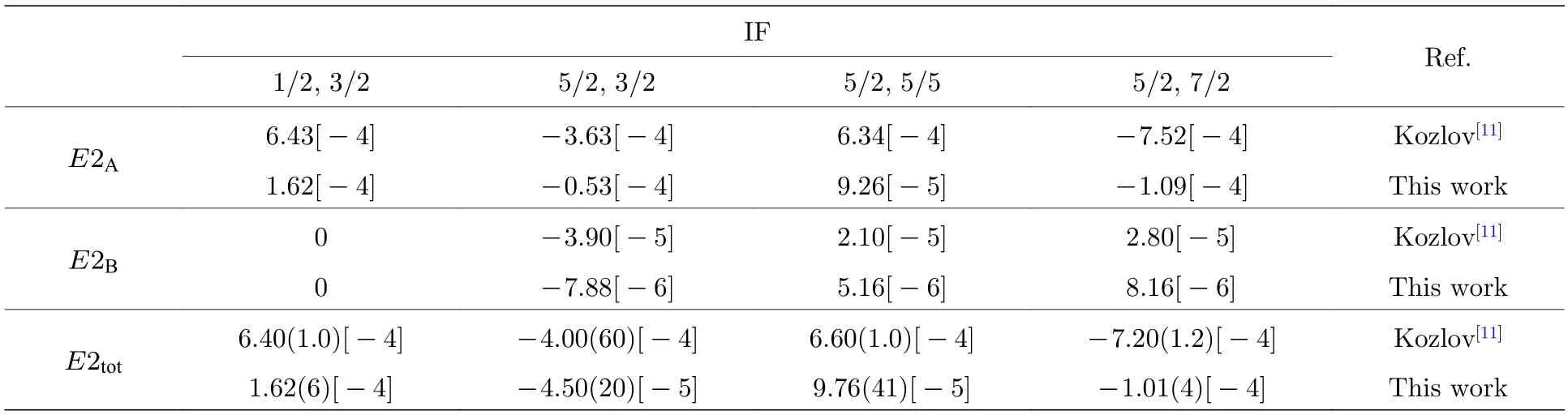
表8 171Yb和173Yb 的超精细诱导 5d6s3D1IF′ →6s21S0 E2 跃迁的跃迁幅度. E2A与E2B 分别表示磁偶极超精细相互作用与电四极超精细相互作用下的诱导跃迁幅度. E2tot 表示磁偶极与电四极超精细相互作用共同作用下的诱导跃迁幅度.方括号内的数值代表以10 为底的指数,圆括号内的数值代表误差Table 8. Transition amplitude of the hyperfine-induced 5d6s3D1IF′ →6s21S0 E2 transition in171Yb and173Yb .E2A and E2B represent the induced transition amplitudes under the magnetic dipole hyperfine interaction and electric quadrupole hyperfine interaction,respectively. E2tot denotes the induced transition amplitude under the combined influence of magnetic dipole and electric quadrupole hyperfine interactions.The numerical values in square brackets denote the exponentiation with base 10,while the values in parentheses represent the error.

通过两种方法来评估超精细诱导跃迁概率的计算误差: 1)规范一致性引起的误差;2)剩余电子关联效应引起的误差.对于前一种误差利用如下公式计算:

其中,RL和RV分别是长度规范和速度规范下计算的跃迁概率.而对于后一种误差,将n=4 的CC关联效应对跃迁概率的影响作为剩余电子关联效应引起的误差.最终,取两种方法中误差较大者作为最终的计算误差,评估后的误差展示在表7 和表8 中.

5 结论

本文基于MCDHF 理论,计算了171Yb和173Yb原子超精细诱导5d6s3D1,3IF′→6s21S0E2 跃迁的跃迁概率.同时,详细分析了不同微扰态和不同超精细相互作用的跃迁概率的贡献.通过计算发现,微扰态3D2与3D1,3D3之间的磁偶极超精细相互作用占主要贡献.此外,3D1→1S0M1 跃迁和超精细诱导E2 跃迁的跃迁概率之比约为450∶1.

结合计算所得的3D1,2,3态核外电子在原子核处的电场梯度和实验测量的超精细常数B,重新评估了173Yb原子核电四极矩Q(173Yb)=2.89(5)b .该工作利用原子物理方法评估了173Yb 原子核电四极矩值,评估结果与目前被推荐的结果符合得很好.