基于里德伯原子Stark 效应射频电场测量灵敏度研究*

韩小萱 孙光祖 郝丽萍 白素英 焦月春

1) (太原师范学院物理系,晋中 030619)

2) (太原学院材料与化学工程系,太原 030032)

3) (山西师范大学物理与信息工程学院,太原 030031)

4) (山西大学激光光谱研究所,量子光学与光量子器件国家重点实验室,太原 030006)

里德伯原子极化率大,在外加电场作用下原子能级发生Stark 分裂和频移,可实现里德伯原子高灵敏电场传感器的研究.采用Shirley 的简化不含时Floquet 哈密顿量模型,计算了Cs 里德伯原子的AC Stark 能谱,修正后与实验上测得的弱场中Cs 里德伯原子的DC Stark 离子能谱拟合,在获得60D5/2 和70D5/2 里德伯原子态极化率 αDC 的同时实现低频弱场灵敏度的计算.并计算了Cs 里德伯原子60D5/2 态频率在0—500 GHz范围内振荡电场中的AC Stark 能级频移量,对里德伯原子传感器在其宽光谱范围内的灵敏度进行定量分析,实现任意场频率最佳灵敏度的计算,为里德伯原子传感器的研究提供理论基础.

1 引言

里德伯原子是一种主量子数n很大(n＞ 10)的高激发态原子,具有半径大[1]、寿命长[2]、电偶极矩强[3]、极化率大[4]、相互作用强等奇异特性,这些特点使其成为目前原子分子领域的研究热点.由于里德伯原子极化率大且对外加电场非常敏感,当外加电场时,原子的能级会发生分裂现象,这种现象称为Stark 效应.这种奇异现象的发现引起了国内外广大学者的广泛关注.

近年来,随着量子计算和量子精密测量的蓬勃发展,量子领域逐渐进入人们的视野,被人们接受、发展并应用.里德伯原子AC Stark 效应的研究最早可追溯到20 世纪初,德国物理学家Johnnes Stark 发现在强电场作用下原子谱线分裂成几条,这种现象被称为Stark 效应.此后,Stark效应便引发了世界众多学者的思考与研究.在1965 年,Shirley[5]提出了Shirley 模型,即用一个无限矩阵表示与时间无关的哈密顿量代替半经典含时哈密顿量.Shirley 模型提供了一种确定共振跃迁概率的简便方法,包括频移和多量子跃迁.在2020 年,Meyer等[6]利用Shirley 模型大大提高了计算Rb 里德伯原子AC Stark 频移的运算效率,还保证了其计算的准确性.在2020 年,Jing等[7-9]重点阐述了里德伯原子微波电场计、基于缀饰里德伯原子微波超外差接收机以及超冷原子微波电场测量的技术方案和结果,提出了一种提升里德伯原子微波天线灵敏度指标的可行技术方案.同时,基于里德伯原子AC Stark 效应在突破传统电子学传感器的工作带宽限制基础上,实现了超宽带连续频谱范围内射频电场测量和微弱载波通信[10-24].

本文采用Shirley 模型对Cs 里德伯原子传感器灵敏度进行定量分析.根据简化不含时Floquet理论,在简化基矢量的情况下,高效准确地计算了不同射频电场频率里德伯态的 Stark 频移量,并与实验获得的Stark 能谱相比较,获得的里德伯态极化率理论值与实验值相吻合,同时计算出任意场频率下的最佳灵敏度.

2 理论模型

2.1 Floquet 理论

在强射频场中里德伯原子能谱出现复杂的态混合和态转移现象,一般采用非微扰Floquet 模型进行分析,实现里德伯原子传感器灵敏度的有效计算[25,26].根据Floquet 理论,含时薛定谔方程表示为

式中H0表示无微扰时里德伯原子的哈密顿量,V(t)表示周期射频场与里德伯原子之间的相互作用,其中V(t+T)=V(t)(ωRFT=2π),T为射频(RF)场的周期,ωRF为射频电场的频率.求解薛定谔方程(1),获得射频场缀饰的里德伯原子含时波函数:

其中W为Floquet 态的本征能量,ψ(t+T)=ψ(t)为周期Floquet 态函数.Floquet 态的傅里叶展开形式可用标准基矢|α〉=|n,l,j,mj〉和ωRF谐波对应的傅里叶基矢|k〉表示为|αk〉=|α〉|k〉,其中〈t|k〉=,则周期含时哈密顿量H(t)=H0+V(t)与波函数Ψ(t) 表示为

在理论计算原子态能级W和Ψ(t) 跃迁概率过程中,基矢|α〉=|n,l,j,mj〉 的选取必须包含所有的耦合态,因为里德伯态混合过程中包括所有可能的角量子数l=0,1,2,···,n-1和j=l± 1/2 值对应态,对于主量子数n的取值,发现一般选n-10—n+10 范围即可.此外,对于射频场存在多光子共振跃迁,这意味着方程(3)和方程(4)每阶分量的Floquet 基矢为标准基矢的几倍.在计算Cs 里德伯原子在射频场下产生的能级频移时,还需要考虑射频场的频率等因素,这极大地增加了计算的复杂程度.同时在求解跃迁概率时需要对时间演化算符U(t+T,t)进行数值积分,而本文仅着重研究Cs里德伯原子的能级频移,因此并未对时间演化算符U(t+T,t) 展开进一步推导.为了简化计算,采用与时间无关Shirley 的Floquet 哈密顿方法,实现任意射频场频率下,Cs 里德伯原子能级频移量的计算.

将上述(3)式和(4)式代入(1)式中,得到一个无限维Floquet 哈密顿量的本征方程:

其中,HF是表示为

当外加射频电场是弱场时,等式(6)中的HF截止到k=±1,这样可以避免时间演化算符U(t+T,t)的积分,同时可以将HF的基矢态简化为与目标态有直接偶极跃迁的里德伯态,以Cs 里德伯态60D5/2为例,这样基矢大小可以从600 多个降低到60 多个,极大提高了计算速度.通过计算Floquet 哈密顿量的本征值和本征矢,便可以确定射频场存在时的能级和基矢态,比较能级相对于H0的变化,即可得到AC Stark 的能级频移量.

2.2 极化率的测量

图1 红色虚线所示为采用时间无关Shirley 的Floquet 哈密顿方法,简化基矢大小计算的Cs 原子60D5/2和70D5/2态mj=5/2 的AC Stark 能级频移量.为了验证计算的准确性,与采用基于二次Stark 效应理论[27]的文献[28]方法数值计算的DC Stark能级进行比较,如图1 黑色实线所示.在与DC电场EDC对比时,EAC=,且AC电场下里德伯能级的Stark 频移量等于均方值下 DC Stark 频移-αDC/2值[29],其中αDC为里德伯态的DC 极化.因此获得里德伯态极化率αDC精确值为验证AC Stark 频移量计算的准确性至关重要.

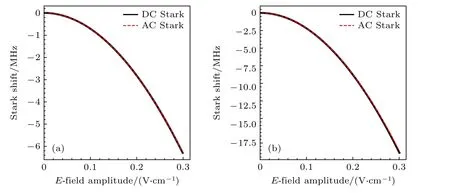
图1 理论计算 Cs 原子(a) 60D5/2,mj=5/2〉和(b)||70D5/2,mj=5/2〉态的Stark 能谱,红色虚线为AC Stark 能谱,黑色实线为校准后的DC Stark 能谱||60D5/2,mj=5/2〉||70D5/2,mj=5/2〉Fig.1.Calculated Stark spectra for Cs Rydberg atom of (a) and (b) state.The red dotted line is the AC Stark spectrum,and the black solid line is the Stark map in a DC electric field on a field axis scaled such that the rms fields.

以Cs 的60D5/2和70D5/2态为例,在一个标准金属磁光阱(magneto-optical trap,MOT)中俘获基态Cs 原子团后,相向入射腰斑为80 μm 的852 nm 的激光(Toptica DL pro)和腰斑为100 μm的510 nm 的激光(Toptica TA SHG110)激发里德伯原子,之后施加电离里德伯原子的斜坡脉冲电离电场,产生离子信号经微通道板(microchannel plate,MCP)进行探测,获得里德伯原子激发谱.在MOT 中心激发区域外侧沿x,y,z三个方向各放置一对电极,用于补偿系统周围的杂散电场.同时,通过扫描x方向电极板的电压获得如图2 所示70D5/2态mj=1/2,3/2和5/2 的DC Stark能谱,将其与数值计算的DC Stark 能级谱(图2 实线)进行比较,获得||70D5/2,mj=5/2〉极化率αDC的实验和理论值分别为835.18 和833.77 MHz·cm2/V2,同样获得||60D5/2,mj=5/2〉极化率αDC的实验和理论值分别为281.19 和280.93 MHz·cm2/V2,如表1 所列.用获得的极化率αDC实验值对Cs 原子60D5/2和70D5/2态mj=5/2 的AC Stark 频移量进行校准如图1 红色虚线所示,其与计算的DC Stark 频移如图1 黑色实线所示吻合得很好.采用与时间无关Shirley 的Floquet 哈密顿方法计算里德伯原子AC Stark 频移量,在提高计算速度的同时,保证了计算的精确度.

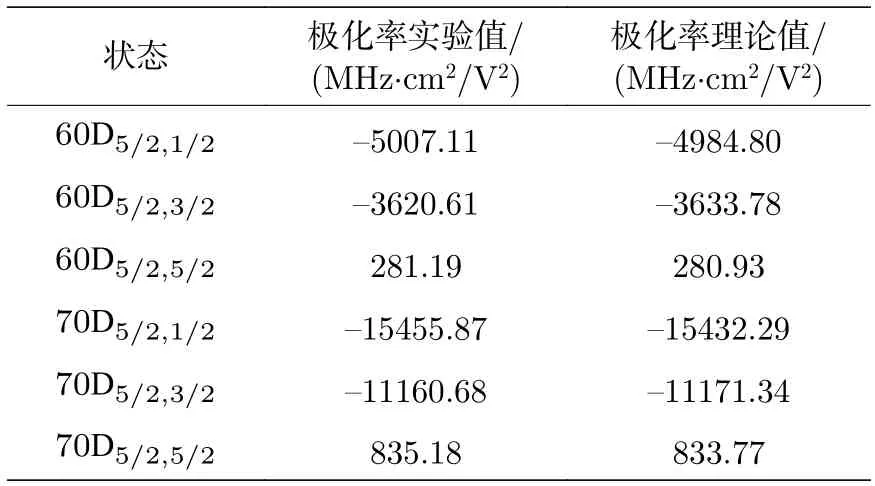
表1 实验测量极化率与计算60D5/2 和70D5/2 态极化率的比较Table 1. Comparisons of the measurement and calculation of the polarizability for 60D5/2 and 70D5/2 Rydberg atom.

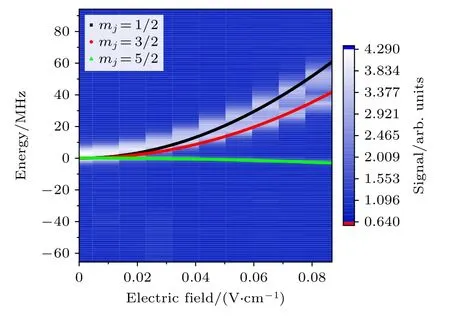
图2 实验测的x 方向70D5/2 里德伯原子 Stark 谱,黑、红和绿色点线分别为理论计算的mj=1/2,3/2 和5/2 的Stark谱Fig.2.Measurements of the Stark spectrum for 70D5/2 Rydberg atom in the x-direction,and the black,red,and green dotted lines show the calculation Stark spectra of mj=1/2,3/2,and 5/2,respectively.

图3 展示了射频电压为ε=100 mV/m,频率在0—500 GHz 宽带范围内,采用Shirley 模型简化基态矢量计算的Cs 60D5/2态AC Stark 频移量.当频率较低时,频率对AC Stark 频移量的影响很小,频移量几乎保持不变.但随着频率的不断增大,当频率约在3.18 GHz 时,AC Stark 频移量出现了第1 个峰值,该峰值频率对应于61P3/2态与60D5/2态的能级差.之后在14.85 GHz,20.03 GHz 和39.03 GHz 等多处出现明显的频移量,分别对应58F7/2,57F7/2和62P3/2态等其他态对60D5/2态AC Stark 频移量的影响.并且在80—90 GHz 之间第1 次出现1 组频移量显著减小的情况,这主要是60D5/2附近态的共同作用显著抑制了AC Stark 频移.因此,时间无关Shirley 的Floquet 模型在减小基矢态数目,保证计算精确度的同时,可以实现宽频带射频场AC Stark 频移量的计算,体现了Shirley 模型计算的高效性.

图3 Cs 里德伯原子60D5/2 态在 ε=100 mV/m 不同频率射频场中的AC Stark 频移,其中临近的共振态用黑色虚线标定Fig.3.AC Stark shifts of the 60D5/2 state in RF field with ε=100 mV/m.The adjacent resonant state is labeled with a black dashed line.

3 里德伯传感器的灵敏度

里德伯原子传感器往往是将光泵浦后的里德伯叠加态与被测电场相互作用,通过测量初始态的集体相移来实现电场测量.其中相移可用信噪比ϕ/Δϕ来表征,假设相位噪声Δϕ为标准量子极限,即ΔϕSQL=1/,N为原子数.ϕ=Ωτ是在演化时间τ内两量子态由原子频移Ω引起的相位变化.演化时间τ取决于有限相干时间Tc和测量时间t.当t ＜Tc时,演化时间τ=t;当t ＞Tc时,光泵浦的里德伯叠加态会在测量时间内破坏并被再泵浦,这种重置会导致观察到原子系综相移减小,演化时间τ=.在测量中相干时间Tc受到原子热运动等影响,以里德伯电磁感应透明效应线宽约10 MHz 为例,假设热里德伯原子系统Tc为100 ns.

在电场频率远低于里德伯原子共振频率情况下,电场强度较弱时可用DC Stark 频移Ω=-1/2αDCε2来估计由射频电场引起的能级频移Ω,则信噪比等于1 的电场值表示为

图4 为利用等式(7)计算的低频DC 场中||60D5/2,mj=1/2〉态里德伯原子传感器的灵敏度,其中红色实线、红色虚线、黑色实线、黑色虚线分别为原子数N=103,104,105,106对应射频电场灵敏度随频率的变化.由图4 可知,当原子数N相同时,射频电场灵敏度随频率变化非常小.εRydberg越小,需要的原子数N越多.当选择的原子数N过大时,里德伯原子密度增大,里德伯-里德伯相互作用增强导致复杂的离子形成.同时考虑到标准量子极限和计算方便,所以原子数N选择103或104最佳,||60D5/2,mj=1/2〉里德伯态极化率αDC取表1 中理论计算值-4984.80 MHz·cm2/V2,其中N=104、测量时间为1 s 的最小可检测场可达0.1 mV/m.且在得知某一已知原子数N、测量时间为1 s 的最小可检测场值,其他原子数N的最小可检测场值都可通过(7)式中原子数N的比值关系直接计算得到.等式(7)中测量弱场灵敏度与极化率平方根成反比,为了提高测量弱场ε灵敏度,Jau 和Carter[30]在被测弱场中叠加一个已知强场Ebias≫ε来放大被测弱场的影响,且传感器的信噪比与Ebias呈线性变化.假设电场偏差的不确定性和噪声小于标准量子极限,该技术可将最小可检测场提高到线性尺度:

其中n=100 的里德伯原子在ωRF＜10 kHz 时的灵敏度优于1(mV·m-1)/

随着射频场频率的增大,里德伯原子对电场感应越发敏感.当ωRF＞100 MHz 时,里德伯原子Stark 频移取决于原子间偶极跃迁共振和非共振相互作用.以两能级系统为例,当射频耦合场失谐远低于两能级之间的跃迁频率时,两能级的AC Stark频移能量为

其中Ω=dε/ℏ 为射频场的谐振拉比频率,ε 为射频电场强度,d为跃迁矩阵元,Δ为射频场的共振失谐量.在共振附近,Stark 频移采用Autler-Townes分裂的形式(AC Stark 效应的一种特殊情况),与n2ε成正比.非共振频移采用一般AC Stark 频移的形式,与n7ε2成正比.我们使用上述两种机制计算不同电场频率里德伯态的AC Stark 频移,将分别计算的每个两级系统的贡献相加,可以得到来自附近多个能级的总Stark 频移,如图3 所示,从而获得任意载波频率的最小可检测场.为此,采用Shirley 理论来估计适用于任意载波频率的最小可检测场,可以实现频率从10 kHz[31]—1 THz[32]的电场灵敏度的测量.

里德伯原子传感器具有自校准能力,测量信号可以通过射频场失谐最近的共振来确定外加射频场频率.以||60D5/2〉→||61P3/2〉 共振为例,图5 为计算的射频耦合场灵敏度和信噪比缩放因子β(信噪比∝εβ)随耦合失谐量增大的变化趋势,其中三角形、正方形和五边形分别对应β=1,1—2 和2的最小可检测场值.如图5 红色实线所示,β 从1到2 过渡的精确宽度和过渡点只取决于射频场强度,因此对于任何共振里德伯态β 值的变化趋势一致,通过β 值,可以确定1 s 测量时间射频电场ε的信噪比.例如,在β=1的区域,如果ε1s=1 μV/m,那么相同频率的100 μV/m 场在1 s 测量时间预期信噪比为(ε/ε1s)β=100.在测量时间t ＞Tc时,射频带宽最小可检测场为εt=ε1st-1/2β,在已知1 s最小可检测场和β值,可以实现任何频率电场灵敏度的实时监测.比如已知ε1s=1μV/m和β=2,则t=1 ms 测量中的最小可检测场为5.6 μV/m,所以通过计算的任意里德伯态AC Stark 频移可实现任何频率电场灵敏度的实时监测.

图5 测量时间为1 s 的最小可检测场和信噪比缩放因子β (红色实线)与||60D5/2〉→||61P3/2〉 射频共振失谐量的关系,其中三角形、正方形和五边形分别对应β=1,1—2和 2Fig.5.The minimum detectable field in a 1 s measurement and the scaling of the SNR (red solid),β,versus detuning of RF transition from the||60D5/2〉→ ||61P3/2〉 .The triangle,square,and pentagon symbols match correspond to β=1,2 or somewhere in between,respectively.

4 结论

本文主要采用Shirley 的简化Floquet 模型研究了Cs 里德伯原子Stark 频移光谱,实现对振荡电场灵敏度的定量分析.理论上对比二次Stark 效应理论方法和Shirley 模型计算的60D5/2和70D5/2,mj=5/2态DC Stark 和AC Stark 频谱,验证了Shirley 模型的可靠性,并与实验获得的里德伯Stark能谱拟合,获得极化率值.同时利用Shirley 模型简化基矢的特点快速又高效地计算了60D5/2态射频电压为100 mV/m,频率在0—500 GHz 宽带下里德伯态的AC Stark 频移量,并引入信噪比缩放因子β计算出了任意场频率下的最佳灵敏度,为里德伯传感器在射频场校准和测量等方面提供理论依据.