平头孔板的初生空化特性定量分析

戚建祥，艾万政

(1.浙江国际海运职业技术学院，浙江舟山 316021；2.浙江海洋大学船舶与海运学院，浙江舟山 316022)

在中国，坝高300 m 级的水电站大坝越来越多，如云南白鹤滩水电站大坝、四川省双江口水电站大坝、金沙江溪洛渡水电站大坝和乌东德水电站大坝等。高坝泄放洪流携带有超大能量，广大水电工作者需要解决的一大重要课题就是研究高坝下泄水流的巨大能量如何消杀掉[1]。传统的外部消能工建设，由于需要占据较大的空间，已经不太适合在峡谷地区水电项目消能。况且外部消能具有一个严重问题就是雾化影响，对周边环境也带来不可避免地破坏。孔板消能工只需要建造在由临时导流洞改建的泄洪洞内，不但建造方便，并且可以克服外部消能引起的雾化影响，目前它是一种比较优化的峡谷高坝消能方法。50 多年以前，和孔板具有相似特性的洞塞被应用到加拿大麦加大坝来消能，当时泄洪洞内安装了三级洞塞，其总消能效率达到50%,取得了很好的消能效果，开辟了孔板式洞内消能工应用于实际工程的先河。

图1 为平头孔板平面示意图型。因为孔板的特别构造，水流流经孔板过程中将遇到突缩和突扩的变化，这就导致孔板上下产生水流的回旋区，从而使水流流体内形成强摩擦力和强剪切力，结果使洪流携带的超大能量在孔板上下附近消杀掉。国内外专家普遍认为，孔板的初生空化特性与其抗空化破坏的能力成反比；孔板的能量消杀系数与孔板的消能功效成正比。关于孔板的初生空化特性及能量消杀系数，王德昌及BULLENETAL,et al 认为，孔板的初生空化特性及能量消杀系数跟孔板孔径比β 紧密关联(β=d/D，式中d 为孔径，D 为大坝泄洪洞的直径，见图1)，孔径比跟孔板的初生空化特性成反比，跟孔板的抗空化破坏的能力成正比，β 越小，孔板能量损失系数却越大，消能效果就会更好[2]。之前同行分析研究了许多孔板的水力学特性，他们也得到一些重要的结论，但是他们关于孔板初生空化数和能量消杀系数问题的研究大多停留在定性分析层面，他们的结论虽然对实际工程有指导价值，但是还不太适合在实际工程中的直接应用。究竟孔板的能量消杀系数、初生空化数与相关体型要素和水力要素的定量关系如何，对这一问题有待于进一步深入开展研究。本文的目的，主要是针对平头孔板，研究其初生空化数与其体型要素，如孔径比、孔板厚度，以及与水力要素(如雷诺数)之间的定量表达式，以便为工程设计提供参考。

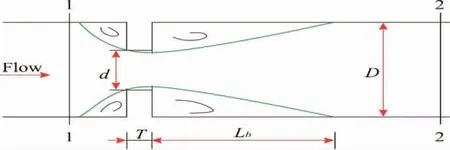
图1 平头孔板Fig.1 Square-edged orifice plate

1 理论分析

孔板初生空化数可按以下公式来定义[3-5]：

式中：p∞为孔板初次发生空化时，孔板前面未扰动断面的临界压强；ρv为水流的饱和蒸汽压；ρ 为水流的密度；u 为泄洪洞水流的平均流速。由于空化首先发生在压强最低处，如果认为空化初生时气泡内充满着水汽，此时ρv应该等于孔板附近的最低压强pmin。按照以上分析，公式(1)也可表达成：

公式(2)中：pmin为孔板附近的最低压强。影响孔板初生空化的因素包括：孔板孔径d(m)；泄洪洞直径D(m)；孔板厚度T(m)；水流的动力粘度μ(N·s·m-2)；水流的平均流速u(m·s-1)；水流的密度ρ(kg·m-3)；压强差(p∞-pmin) (Pa)。由于以上参数都是独立变量，且这些变量同时也为(p∞-pmin)的函数，因此可以得到：

上式可以改写成：

结合公式(1)和公式(4)，可以得到：

公式(5)中：Re=uDρ/μ 指管道水流雷诺数；β 为孔径比；a=T/D 为厚径比。公式(5)表明：平头孔板的初生空化数为孔径比、厚径比及雷诺数的函数。

2 数值模拟研究

2.1 数值计算模型

本文采用的数值模拟模型为RNG k-ε 模型。RNG k-ε 模型的控制方程包括[6-7]：

公式(6)-(9)中相关参数为：xi(=x,y)分别代表轴向、径向坐标；ui(=ux,uy)分别代表轴向、径向水流的平均流速；ρ 为水流密度；ν 为水流动力粘度；νt=Cμ(k2/ε)为涡粘度，ε 为紊动能的耗散率，k 为紊动能，Cμ取值为0.085。其他参数的取值分别是：，η=Sk/ε，C1=1.42，，ηo=4.377，λ=0.012，Gk=ρvt，C2取值1.68，αk和αε取值均为1.39 。

入流边界、出流边界、壁面边界以及对称轴边界均为计算涉及的边界条件。各个边界条件的确定方法如下：(1)入流边界条件跟入流平均流速、湍流动能耗散率和湍流动能分布有关。其数学表达式分别是：uin=u0；k=0.0144u20；ε=k1.5/(0.5R)，式中：u0为入流平均流速；R 为大坝泄洪洞的半径。(2)出流边界的条件：考虑水流均从泄洪洞充分泄出。(3)壁面边界的条件：采取常用的壁函数法，即边界层流中取值无滑移假定，也就是假定边界节点速度分量数值跟壁面边界速度数值是相等的。(4)对称轴边界的条件：设定径向的速度忽略不计，同时每个变量在径向方向的梯度也忽略不计。

2.2 计算方法

因孔板泄洪洞的标准轴对称特点，我们常把孔板泄洪洞的三维模拟计算简化成二维模拟计算来分析。图2 标注的坐标是泄洪洞的三维数轴，因其轴对称特性，这里仅分析图中XZ 方向的二维坐标轴的泄洪洞水力学特性，用其来代表孔板三维泄洪洞的水力学特性[8]。

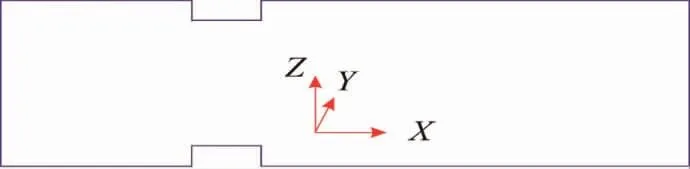
图2 孔板泄洪洞的坐标轴示意图Fig.2 Schematic diagram of coordinate axis of orifice spillway tunnel

计算中用到的泄洪洞直径D 取值选择0.21 m。计算的长度为从孔板上下6D 的长度范围。p∞取值孔板上游0.5D 处断面的平均压强，初生空化数按照公式(2)来计算。计算网格的划分见图3。按照已有的研究成果可知，孔板的最低壁面压强一般出现在孔板后缘附近。孔板下游壁面最低压强的确定方法，直接关系到数值模拟的精度。关于孔板最低壁面压强的确定，此处采取的方法为：每次数值计算以后，在孔板后缘0.25D 的X 轴范围内，等间距取出50 个断面，每个断面沿Z 轴方向又平均取出200 个等间距点，查看每个断面上各点的最低压强，将此50 断面中的最低压强点的压强近似看作是孔板后的最低压强。这种确定最低压强的方法不但计算工作量大，而且对于最低压强的确定也不可避免地带来一定的误差。当然，断面间距取得越短、每个断面的点取得越多，对于确定的最低压强误差也越小。但是，无论是物理模型试验还是数值模拟计算，想完全精确找到最低压强点，几乎无法实现，因此一定的误差总是存在的，只要做到误差控制在一定范围内，其误差对本文所阐述的问题并不影响。本文以一个标准大气压作为计算用到的操作压强，因此孔板下游很多地方将出现负压，但并不影响本文对初生空化数的研究。

图3 网格的划分Fig.3 Grid division

2.3 计算结果讨论

表1 是计算得出的当β=0.50，α=0.50 时的孔板初生空化数。观察表1 数据可以发现，当雷诺数到达105数量级时，其对初生空化数的影响较小。如果忽略雷诺数对平头孔板初生空化数的影响，则公式(5)可以简化为:

表1 初生空化数随雷诺数的变化(β=0.50,α=0.50)Tab.1 Variation of incipient cavitation number with Reynolds number (β=0.50,α=0.50)

表2 为当雷诺数为1.8×105时，计算得出的孔径比及厚径比不同下的孔板初生空化数。由表2 中的数据可以看出，平头孔板的厚度对其初生空化数的影响也比较微弱，因此，也可以忽略厚度对初生空化数的影响。利用表2 中a=0.1 时各种孔径比下的初生空化数数据，可以绘制成图4。在初生空化数的影响因素中雷诺数及厚度忽略不计的基础上，绘制成图4 的曲线，从而得到平头孔板的初生空化数经验表达式：

表2 各种孔径比和厚径比下的初生空化数(Re=1.80×105)Tab.2 Icipient cavitation number under various aperture ratio and thickness diameter ratio(Re=1.80×105)

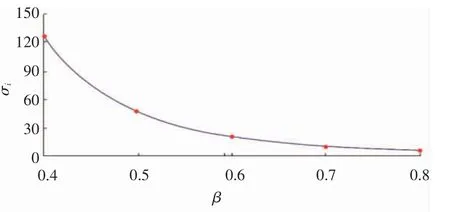
图4 孔径比变化导致初生空化数的变化Fig.4 Change of initial cavitation number due to change of aperture ratio

公式(11)的适用范围为：β=0.4～0.8,α=0.5～2.0 且Re＞105。

3 试验研究

利用减压箱进行物理模型试验，孔板下面都设置了空化噪声测量系统。如图5 所示为空化噪声测量系统。

图5 空化噪声量测系统Fig.5 Cavitation noise measurement system

初生空化的判断方法如下：通过对比测量的噪声频谱与背景噪声，当声压级差达到5～10 dB 左右时，就可认为发生初生空化，此时可测量公式(1)中的相关参数来计算初生空化数。公式(1)中的pc 在减压试验中被分为两部分：pc=pu+pa

上式中：pu为孔板前0.5D 断面处压强，pa为减压箱中压强。为了验证公式(11)的合理性，孔径比为0.6、0.7、0.78、0.8 时的初生空化数被测量。如图6中的(a)图是测量出的孔径比为0.6 时的背景噪声的声压级(单位dB)，图6 中的(b)图是测量得出的孔径比为0.6 时的空化初生时的噪声声压级。比较(a)和(b)两图发现，两图背景噪声的声压级差达到了9 dB 左右，此时可认为(b)图是空化初生时的噪声频谱。

图6 噪声频谱(β-0.6)Fig.6 Noise spectrum(β=0.6)

图中横坐标为背景噪声(单位为Hz)，纵坐标为对应背景噪声的声压级(单位为dB)

测量的结果见表3。利用表3 的数据和公式(11)，可以绘制出图7。从图7 可以发现，公式计算值与试验值的最大误差小于13.5%，实测值与公式计算值吻合较好。

表3 初生空化数测量结果Tab.3 Measurement results of incipient cavitation number

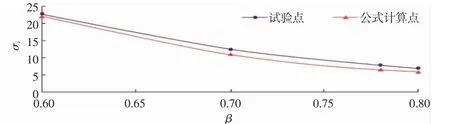
图7 公式计算结果与实测结果比较示意图Fig.7 Schematic diagram of comparison between formula calculation results and measured results

4 结论

针对平头孔板的研究发现，其初生空化数与雷诺数、孔板厚度、孔径比等因素紧密相关。而影响雷诺数的关键因素是孔径比。当雷诺数超过105时，其对初生空化数的影响很小可忽略；同时，孔板厚度的影响也不明显。通过研究说明，平头孔板的初生空化数与孔径比成反比关系。经过大量模拟计算得到的数据绘制成曲线，计算出了平头孔板的初生空化数的经验表达式，创新性地提出了平头孔板的初生空化特性定量分析结论。物理模型试验也证明，平头孔板初生空化数的计算结果与实际测量结果吻合较好，为平头孔板的工程应用提供了重要的参考依据。