泡沫铝有限元仿真模型研究现状

曹梦真，邱田伟，安钰坤，2

(1. 山东理工大学机械工程学院，山东 淄博 255000)

(2. 山东鸿宇风机有限公司，山东 淄博 255300)

1 前 言

泡沫铝是一种由铝合金基体和孔泡复合而成的新材料[1，2]，既具有金属材料的结构特性，又有多孔材料的功能特性。轻质、高比强度、阻尼减震以及电磁屏蔽等特性使泡沫铝材料在建筑、汽车、航天航空等领域拥有广阔的应用前景[3，4]。然而，在泡沫铝的发泡制备中，发泡剂是否均匀分散、孔泡是否稳定，均会显著影响发泡效果进而影响材料性能。为准确模拟实际泡沫铝的性能，构建一个多孔泡沫铝模型是仿真模拟的基础。

有限元法(finite element method，FEM)又称有限元分析(finite element analysis)，由Clough[5]在20世纪70年代首次提出，它作为一种可以用来解决力学问题的数值近似方法，随着计算机的发展不断崛起，被逐步引入多孔金属材料的模拟研究中[6，7]。在建模过程中只需改变相应参数，即可得到不同孔隙分布的模型，缩短试验周期，节约成本提高效率，同时解决泡沫铝样品在实验中不可重复的问题，具有一定的前瞻性。同时，仿真模拟也可作为理论分析和实验测试强有力的工具，预测多孔材料宏观尺度的力学性能和破坏损伤机制，有效解决实际生产中的诸多问题。

目前，有许多微尺度模型可以体现出泡沫铝的结构特性，本文将多孔泡沫铝的仿真模型分为3类：简单晶胞模型、随机模型和三维CT重构模型。本文针对不同类别具有代表性的模型进行详细阐述，并归纳模型的构建方法与研究结果，分析模拟结果与实验结果的差异，对各模型的优势与不足进行深入探究。

2 简单晶胞模型

早期学者对泡沫铝的结构不甚了解，仅用简单实体结构模拟泡沫铝的孔隙，即代表体积单元(representative volume element，RVE)[8，9]，又称为镶嵌法[10]。该三维模型是将一个独立基本单元不断复制与堆砌形成的，多采用简单立方或近球体模拟孔泡形态。RVE法可通过增加晶胞点数或面数提高复杂性，但模型构造方法保持不变。

2.1 立方胞体模型

受金属晶体晶格结构[11]的启发，研究人员通过不断堆砌实体单元构建出多孔材料结构。立方胞体作为最简单的晶格结构，分为简单立方、面心立方和体心立方3类，且此构造方式可以形成具有良好对称性和周期性的高孔隙率几何模型。图1为Libonati等[12]建立的3类立方胞体单胞模型(其参数特性如表1所示)，该模型可在一定程度上模拟泡沫铝的孔隙结构，在准静态压缩状态下呈现典型的线弹性、塑性平台和致密化3个变形阶段，且变形失效模式与实验测试结果高度相关[13]，如图2所示。袁本立等[14]对1/8胞体结构模型沿z轴加载模拟发现，简单立方结构支撑棱柱存在不均匀性，中心位置与节点过渡处部位差异较显著，在结构吻合度方面略逊于面心立方和体心立方结构。刘培生等[15]的八面体模型构造原理与面心立方相似，单元错落有致地分布在3个相互垂直的三维方向上，实现结构整体的密堆积，该模型的承载模拟表明结构状态和承载状态是完全等价的，具有三维同性的优势，然而仅适用于孔隙率大于70%的多孔结构。简单的整体结构使立方胞体模型在模拟孔隙率高于80%的试样时结果较为准确[16]，但它无法模拟复杂多变的孔隙结构，因此建模精度不高，不能真实地反映多孔材料的力学性能。

图1 3种立方胞体单胞模型及三维实体模型[12]Fig.1 Single cells and the three-dimensional solid models of three cubic cell models[12]

图2 基于3种立方胞体模型模拟的准静态压缩下的变形失效模式及与实验结果对比[13]Fig.2 Simulated deformation failure modes of three cubic cell models under quasi-static compression and comparisons with experimental results[13]

表1 立方胞体结构参数及与相对密度的定量关系

2.2 Gibson-Ashby模型

美国麻省理工大学Gibson和英国大学Ashby在研究泡沫铝力学性能时构建了Gibson-Ashby经典模型[17]，如图3所示[18]，该模型由1个孔隙单元和12根相互垂直的棱柱组成，立方框架结构简单均匀且具有各向同性、普适性及广泛的应用价值[19]。同时，Gibson也最早采用三段式分段函数来表征泡沫铝的应力-应变曲线，从细观梁弯曲理论角度展现了线弹性区、屈服平台区和致密化区3个变形阶段，并充分考虑到闭孔泡沫铝的胞壁延展变形，给出了泡沫材料压缩强度表达式：

(1)

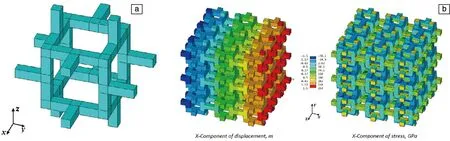
图3 Gibson-Ashby模型[18]：(a) 单胞模型，(b) 拉伸位移及应力云图Fig.3 Gibson-Ashby model[18]：(a) single cell model，(b) tensile displacement and stress contour

Tereza等[19]在建模时通过增加棱柱厚度压缩中央孔洞体积构建了不同孔隙率的Gibson-Ashby模型，并发现该模型对大于70%的高孔隙率材料可实现有效预测，相对电导率和相对杨氏模量的预测结果与实验结果都相差4%左右。Haag等[21]通过实验对比发现，Gibson-Ashby模型只能对几何模型失稳显著的泡沫结构进行稳态蠕变行为预测，且只能预测泡沫蠕变率的下限，具有很大的局限性。刘培生[22]分析发现该模型结构具有无法密堆积、棱柱结构不完全等价等缺点，导致受力效果不够理想以及裂纹扩展方式与受力分析存在偏差。

2.3 Kelvin模型

Kelvin模型的单胞由8个正六边形和6个正四边形组成，具有26个顶点和36根棱边，又称十四面体模型(图4)。该模型单胞可按周期性规则排列填满整个空间，也被认为是最接近泡沫金属的结构模型[23]，在模拟低密度的泡沫金属时更具有真实性。Kelvin模型属于RVE方法中的一种类型，可通过增加几何结构的复杂性使模型接近真实孔泡。Belardi等[24]及Jang等[25]对传统Kelvin模型进行了改进，建立了沿带离散变化的圆形截面有限元梁模型，并用光束模型校正节点的弹性特性，使该模型在力学性能方面与实体结构的差异大大缩小，且计算量远低于实心Kelvin模型。Zheng等[26]与Duan等[27]分别利用LS-DYNA及ABAQUS/Explicit 2种有限元模拟软件研究了准静态Kelvin模型单胞的力学响应和变形模式，发现变形模式是从加载端逐渐积累应变，并通过渐进堆积完成整体变形。Sun等[28]认为Kelvin模型未考虑顶点对力学性能的影响从而高估了材料的杨氏模量，在应力-应变图中无法准确展现出压缩平台区域。对称分布的宏观Kelvin力学模型无法模拟微观结构对整体的影响，致使所得结果与实验结果存在不少偏差。

图4 Kelvin模型结构建模步骤[23]Fig.4 Modeling steps for Kelvin modeled structure[23]

3 随机模型

由于用宏观力学模型模拟微观结构特征准确度不高，近年来，诸多学者通过构建随机模型来模拟具有高度复杂孔隙结构的泡沫金属的力学行为。与简单晶胞模型同质化连续统一方法不同，随机模型可以模拟泡沫铝发泡成形的过程，实现胞孔随时间/空间的变化，具有非均质多尺度的优势。

3.1 随机胞孔模型

随机胞孔模型可分为二维和三维2种，是将简单胞孔在一定平面或空间随机排布而形成的随机模型，可通过调整胞孔尺寸参数和数量来改变孔隙结构，实现随机模型的整体构建。Dou等[29]结合C++和ANSYS/LS-DYNA软件建立了不同相对密度(20%，30%和40%)的二维随机模型，采用圆形孔泡随机分布的建模方式，探究不同相对密度下微惯性效应对应变率效应的影响。分析发现相对密度越高应变率效应越明显，该结论与实验结果保持一致，但由于孔壁缺陷，模拟值与实验结果相差10%左右[30]。

三维随机模型分为球形、椭球形和多面体形，该类模型构建步骤如下：先构造一个立方体模型，设定孔隙率、孔径范围及最小壁厚等参数，在立方体空间随机生成形核点，使形成的实体胞孔随机排列且不会干涉，最后运用布尔运算即可得到三维随机模型。该法得到的模型孔隙结构更接近真实泡沫铝，且仿真结果与实验结果趋于一致。Fang等[31，32]利用凸多面体模型模拟泡孔隙单元形成泡沫铝模型并映射生成有限元网格，分析发现多孔材料对冲击作用下的能量吸收源于孔壁的塑性变形(图5)。

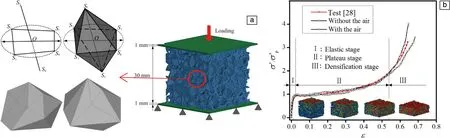
图5 三维随机多面体泡沫铝模型构建步骤(a)和模拟的准静态压缩时的应力-应变曲线(b)[31，32]Fig.5 Modeling steps for three-dimensional random polyhedral aluminum foam model (a) and simulated stress-strain curve during quasi static compression (b)[31，32]

泡沫铝胞孔内的气体在变形时受到细胞壁坍塌挤压，进而推动下一阶段压缩，因此赋予气体参数并考虑空气效应会更接近实验结果。Zhu等[33]通过不同的渐进损伤模型比较孔泡形态对压缩性能的影响，发现椭球形态的孔泡呈现出各向异性几何结构，胞孔内部气体压力对不同方向施加载荷导致非对称变形，进而使材料拥有更高的弹性模量和抗压强度(30～40 MPa)。三维随机模型在建立之初就能够考虑到实际的泡沫铝形态，既有宏观规律性又有微观随机性，推广性和实用性更强。然而模型的模拟过程也会相对繁琐，模型参数的设置比较复杂且随机因素较多，因此编程前的设计准备以及程序运行所耗费的时间和精力会显著增加。

3.2 Voronoi模型

Voronoi模型是利用空间分割方法，通过定义切割点的距离将空间划分为规定个数的无缝单元。Voronoi模型的二维及三维模型如图6所示[34，35]，成形方法是在一个指定的空间中，先生成距离不能小于规定值并随机排列的形核点，以其为中心按相同速率长大形成胞孔，当相邻胞孔彼此相遇时停止生长，边界即为相邻形核点相连的垂直平分线，直至布满整个空间。我国的国家游泳中心“水立方”就是采用了这种构造方式[35]。

图6 Voronoi模型：(a) 2D-Voronoi壳单元模型[34]；(b) “水立方”场馆外墙，(c) 3D-Voronoi几何模型[35]Fig.6 Voronoi model：(a) 2D Voronoi[34]；(b) external wall of the building Water Cube and (c) 3D Voronoi[35]

Li等[36]运用LS-DYNA有限元软件与霍普金森压杆研究泡沫铝试样在70 m/s的速度下的压缩变形行为，实验与模拟所得的应力-应变曲线如图7所示，均呈现典型的线弹性区、屈服平台区和致密化区3个阶段且两数据吻合度较高，表明Voronoi模型具有准确的预测作用。除孔洞结构参数外，基体材料的力学性质也将直接决定泡沫金属的压缩行为和变形模式。程和法等[37]对纯铝及铝基泡沫金属进行压缩试验，纯铝为基体的泡沫铝表现出典型的塑性泡沫特征和较低坍塌屈服强度，铝基泡沫金属呈现典型的脆性泡沫特征和较高的弹性模量及屈服强度。对于三维Voronoi模型，学者多选择理想的弹塑性模型来表征泡沫铝单元壁材料[38]，如采用著名的Cowper-Symonds关系表征母材的塑性变形[39]：泡沫铝基体的典型弹性模量为69～73 GPa，屈服强度为100～300 MPa[40]；或是利用von Mises屈服准则及各向同性硬化塑性材料模型[41，42]，通过静态单轴拉伸实验提取屈服应力及切线模量作为实际参数增加模拟结果准确率[43，44]。

图7 基于Voronoi模型的压缩实验模拟(a)及所得应力-应变曲线及与实验结果对比(b)[36]Fig.7 Simulation for compression test based on Voronoi model (a) and simulated stress-strain curve and comparison with experiment result (b)[36]

Voronoi模型的建模过程模拟了泡沫铝材料随机发泡成形的过程，在表现材料微观结构复杂性的同时提高了计算效率，因此获得广泛应用。然而，二维或三维Voronoi模型因采用随机形核成长的建模方式，每个孔泡边缘处均呈现较为尖锐的边界，与实际的胞孔圆弧边界不符[45]，易造成应力集中等缺陷。此外，Voronoi模型未考虑泡沫铝多孔泡交界处Plateau Border边界的真实形貌，因此该模型分析结果与实际有较大差异。研究表明，该模型与Kelvin模型相比，对泡沫铝材料体积弹性模量的预测结果低20%[46]。为改善Voronoi模型，有关学者通过向模型中加入圆形或椭圆形胞孔来减少模型与实际的偏差，但是该法削弱了随机孔隙优势。此外，Voronoi模型的孔壁厚度是通过壳型建模形成的，其孔壁厚度保持一致，难以实现随机分布，因此当泡沫铝试样孔壁厚度不均甚至相差较大时，模拟结果与实际实验出现较大偏差。

4 三维重构模型

三维重构建模是结合同步辐射X射线计算机断层照相技术(synchrotron X-ray computed tomography，SXR-CT)进行重构，近乎可实现材料结构1∶1无损建模。三维重构模型的精度受SXR-CT的扫描步长和分辨率影响，在工业CT技术迅猛发展的背景下，该模型的研究也日趋增多[47，48]。此外，对于结构比较复杂的闭孔泡沫结构而言，SXR-CT是一种很有前景的小尺度三维结构研究方法，具有较高的空间分辨率，可以在不破坏原始物体的情况下原位观察结构以及特征的变化[49-51](图8)，具有其他模型不具备的真实性和准确性。

图8 三维重构模型构建流程图[51]Fig.8 Flow chart of three-dimensional reconstruction model construction[51]

Li等[49]利用SXR-CT技术建立了三维重构模型，有限元方法模拟的应力应变曲线与该试样的真实测试结果如图9所示，2组数据呈现高度吻合；在结构薄弱处首先出现的压缩面逐渐扩展至整个模型，塑性变形带演化规律与实际测试结果契合度较高。Kader等[52]发现泡沫铝承载时会在孔壁交界处的Plateau Border形成塑性铰(plastichinge)，弯曲力矩的存在降低了孔壁的承载性能，而胞壁的速率依赖性和微惯性取决于结构特性[53]，从而导致孔隙结构的坍塌。目前，基于泡沫铝模型模拟的力学性能与实际测试值之间的误差一般归因于模型构建中忽略了细胞壁的微孔及微缺陷，据统计，直径在30～350 μm范围内的微孔约占金属体积的26%[54]。Zhang等[47]研究发现，在控制微孔缺陷作为单一变量后，垂直载荷和水平载荷方向上的模拟分析结果与真实试样测试结果相比，全局误差分别为15.9%和4.5%。

图9 基于三维重构模型有限元模拟的应力应变曲线及与实验结果对比[49]Fig.9 Comparison of stress-strain curves from finite element method simulation based on three-dimensional reconstruction model and the experiment[49]

Toda等[55]关注到应力松弛发生的微裂纹或微孔偏转，他们通过在孔泡之间建立互连来影响金属泡沫的胞孔结构，进而引起显著的裂纹偏转。Movahedi等[56]则认为孔壁中微孔的存在作为裂纹萌生和扩展源进一步诱导了局部应力集中，从而削弱了泡孔结构强度(图10)。利用三维重构技术可以真实反映出内部微孔的分布，这也是基于三维重构模型的模拟结果更加准确的原因。

图10 内部微孔分布的三维渲染透视图[56]Fig.10 Three-dimensional rendered perspective view of internal micro-pores distribution[56]

然而，由于SXR-CT是基于不同角度的静态图像识别，需要对现有实体进行扫描重构，严重依赖数据收集，因此难以对孔隙率、孔径尺寸及分布、孔泡壁厚及胞孔形状等参数进行反复多次的定量研究[57]。三维重构模型大小受CT分辨率影响，当试样尺寸过大或分辨率要求太高时，需要大型试验设备及专业人员进行繁琐复杂的重构处理。CT图像阈值的设置会直接决定孔隙率的识别情况，进而导致孔泡与铝基体区域的误判。此外，该模型无法实现高通量随机模型的构建，且模型构建成本偏高，这也是制约此技术推广发展的关键因素。

5 结 语

泡沫铝材料由于发泡条件各不相同，胞孔大小、分布以及胞壁厚度复杂多变，关于泡沫铝模型的构建一直都在不断突破与完善。为了分析并预测泡沫铝的承载性能及失效模式，本文分析并讨论了现有的几种泡沫铝有限元模型的优缺点，分别是：以代表体积单元构建的简单晶胞模型，该模型结构简单，但无法反映实际的多孔结构；以随机形核点构建的非均质多尺度随机模型，可实现孔壁和孔泡数目的参数设定；运用X射线衍射及图像重构技术的三维重构模型，可实体1∶1无损建模并能精确反映泡沫材料的微观结构。

泡沫铝材料内部孔隙具有复杂性和随机性，使材料在承载时表现不同的失效模式，为此寻求并构建一种可精确反映泡沫铝随机孔隙结构的孔泡模型，准确且简单地表征出实际泡沫铝的结构特点并具有一定实用性和推广性，仍是泡沫铝材料数值模拟研究的重要一步。