基于强化学习的多技能项目调度算法
2024-05-11胡振涛崔南方胡雪君雷晓琪
胡振涛,崔南方†,胡雪君,雷晓琪
(1.华中科技大学管理学院,湖北武汉 430074;2.湖南大学工商管理学院,湖南长沙 410082)
1 引言
现代项目中存在着一类多技能资源,如R&D行业的多技能研发人员、工程项目中的多功能作业车等[1].这使得多技能项目调度问题(multi-skilled project scheduling problem,MSPSP)[2]成为近年来学者们关注的热点.在项目调度研究领域,资源的指派是最重要的研究内容之一,它不仅能影响项目的工期,还能影响调度计划的鲁棒性[3]、项目产品的质量[4]等.与传统的资源受限项目调度问题(resource constrained project scheduling problem,RCPSP)相比,MSPSP中资源的多技能特征增加了资源指派的难度,因为在多技能项目调度中,在为活动指派资源的同时,还要为资源指派技能,问题的维度增加,求解难度也更大.
MSPSP 属于NP 难问题[5].作为组合优化问题,MSPSP中活动、技能和资源间可能出现组合爆炸.精确求解算法只能求解规模极小的算例[6].因此更多的研究集中于启发式和元启发式算法.如Almeida等[7-8]和胡振涛等[9]根据多技能资源的特征分别设计了基于静态资源权重和基于动态资源权重的启发式方法.Laszczyk等[10]、Javanmard等[11]和Tabrizi等[12]则设计了遗传算法予以求解,此外禁忌搜索[13]、蚁群算法[14]、差分进化算法[15]等也常被用于求解MSPSP.然而启发式算法往往需要根据项目特征设计规则或参数,导致算法迁移性较差.元启发式算法虽然通用性较强,但在求解大规模项目案例时常需要很长的时间才能求得满意解.此外,由于这些算法涉及的参数较多,加之项目调度问题自身的复杂性,算法的设计和使用常需要较深的专业知识辅助[16].
机器学习作为近些年的热点研究对象,被广泛应用于计算机视觉、自然语言处理等领域.强化学习作为机器学习的方法论之一,具有参数少、迁移性强等优点,且在求解组合优化问题方面也有了显著的成果,如围棋游戏问题[17]、车间调度问题[18]、旅行商问题[19]等.而项目调度过程很容易建模为马尔科夫决策过程,这为应用强化学习算法提供了条件.此外,项目调度模型往往是明确的,如工序约束、资源约束和时间约束等,这为强化学习的采样提供了便利.如Sallam等[20]针对单技能项目调度问题,考虑了差分进化和布谷鸟算法,并以强化学习作为算法优选技术,在进化过程中从两个算法中选择其一;Sung等[21]针对存在活动反复的单技能项目中的资源分配问题,设计了强化学习算法.此外,Gai等[22]和Mao等[23]也将强化学习算法应用于求解项目调度中的资源分配问题.
从现有文献看,项目调度问题应用强化学习的研究主要集中在近几年,且研究成果不多,尤其是针对多技能项目调度问题,尚未发现有深入的研究.基于此,以下第2部分构建了多技能项目调度问题的数学模型;第3部分在介绍强化学习算法和项目调度问题的基础上,针对工期最短的MSPSP设计了基于强化学习的求解算法;第4部分为数值实验及结果分析;第5部分总结了研究内容并提出了下一步的研究方向.
2 问题建模
项目网络采用节点式(AON)表示,共包含n个活动节点,其中起始节点1和终止节点n代表虚活动;活动之间存在工序约束;以G=(V,E)表示项目网络,其中V={1,···,i,j,···n}表示活动集合,E为有向弧,表示活动的工序约束;活动i的工期是为di,对技能l的需求量为TFil;资源具备多技能,R={1,···,k,···,K}表示资源集合,资源总量为K,RFkl表示资源的技能禀赋,当资源k可执行技能l时RFkl=1,否则RFkl=0;F={1,···,l,···,L}表示技能集合,技能种类为L.
在以项目工期最短为目标函数的MSPSP模型中,决策变量有两个,即活动的开始时间Si,以及活动的资源分配xkli,当xkli=1时,表示资源k以技能l的形式被分配到活动i中去.相应的模型如下:
其中: 式(1)表示目标函数;式(2)表示工序约束,其中Pj表示活动j的紧前活动集合;式(3)表示资源只可执行其所掌握的技能;式(4)表示各活动的技能需求必须得到满足,且不会被分配到过多的资源;式(5)表示资源在一个活动中最多只能执行一种技能;式(6)表示两个活动不可互为前序,其中当活动i在活动j开始之前已完工时qij=1,否则qij=0;式(7)表示并行的活动不可使用同一资源;式(8)表示决策变量的可行域,T ∈{0,1,···,t,···}表示时间点集合.
3 算法设计
采用不同算法求解项目调度问题时,需要根据相应的算法逻辑解构问题,如基于规则的启发式算法需要根据规则解析项目的特征参数,元启发式算法在编码和解码时需要耦合项目的调度过程.以下将结合强化学习的算法逻辑,根据算法思想解构多技能项目调度过程,设计基于强化学习的多技能项目调度算法(reinforcement learning-based parallel scheduling algorithm for multi-skill project,RLP).
在强化学习(reinforcement learning,RL)中,智能体(Agent)在环境(Environment)中处于不同状态(State)时,根据不同策略(Policy),尝试各种行动(Action),并被环境回馈以不同的奖励(Reward),一次“状态-行动-获得奖励-新状态-新行动-···”的过程,称为一个回合(Episode).主要过程如图1所示.
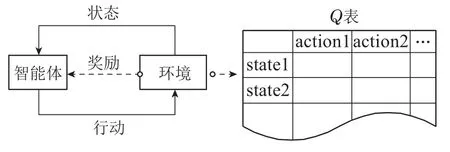
图1 强化学习过程Fig.1 Process of RL
强化学习将问题建模为马尔科夫决策过程(markov decision process,MDP),可用一个四元组表示,即MDP={State,Action,P(a|s),R(a|s)},元组内分别代表状态空间、行动空间、状态转移概率和回报函数.其中状态指的是智能体每次决策时所处的状态,具体到项目调度问题中,是每次决策时的活动、资源或其他项目要素的状态,状态信息越全面,价值函数便越精确,同时其值空间也越大;行动是智能体每次迭代时所做的决策,在项目调度问题中,背景和目标函数的不同,行动的内容也不同;强化学习的最终目的是通过更新价值函数获得一个最优策略使得整个事件的总回报(Return)最高,这里的回报即是所求解问题的目标函数.价值函数需要考虑的因素有两个:奖励和回报.奖励一般指即时奖励,是在一步行动后所获得的收益.回报一般指长期收益,是完成一个MDP的收益和后续行动的奖励之和.在项目调度问题中,奖励和回报与目标函数有关,以工期最短为目标,则奖励和回报便和项目工期大小负相关.
3.1 基于并行调度的MDP模型
项目调度的本质是活动排程和资源分配.并行调度(parallel scheduling generation scheme,PSGS)和串行调度(serial scheduling generation scheme,SSGS)作为两种最常见的项目调度计划生成方式[20],都是通过迭代将项目活动一一加入到调度计划之中,是一种严格的MDP,这为项目调度问题应用强化学习算法提供了条件.引入一个多技能项目案例,项目网络及活动参数如图2(a)所示,资源数量为4,技能数量为3,资源技能矩阵为[0 1 0;1 0 1;1 0 1;1 0 0].图2(b)-(f)表示该项目调度过程中的甘特图,坐标系内的方块表示加入调度计划的活动,虚框内的方块表示未加入调度计划的活动.可以看出,该项目的调度过程是一个包含5个状态、4个行动的MDP,其中状态表示当前排程状况,行动表示从未排程活动中选择一个加入调度计划.如图2(b),state1表示当前状态尚未有活动加入排程,action1表示当前选择了活动2加入排程,达到新的状态state2,即图2(c).依照这种方式,直至所有活动加入排程,并达到state5,调度结束.

图2 项目调度的MDP过程Fig.2 MDP of project scheduling
PSGS随时间迭代[24],在每个决策时点t,从当前不违背工序及资源约束的活动集中选择活动加入排程,直至调度完成.用表示在时点t已排程的活动,用表示在时点t未加入排程的活动,可知
从PSGS 的角度,项目调度过程是包含n-1个状态和n-2个行动的MDP.在时点t,其完备的状态空间是及其内活动和资源的详细排程,即
在决策时点t,行动是从中选择一个活动加入并为之分配资源,以Rtj表示在时点t活动j的一个可行的资源方案,则时点t完备的行动空间是为
在每个回合内,所选活动的开始时间便是当前决策时点,这降低了行动空间的维度,此时的行动空间可以用式(11)的二元组表示.
尽管如此,结合式(10)-(11)可以看出,二者仍极易产生组合爆炸.尤其是在MSPSP中,一个活动往往有很多种可满足其技能需求的资源分配方案,这导致式(11)中{Rtj|j ∈}元素过多,使得状态与行动作为组合之后的再组合,其规模将呈现指数级增长.过于庞大的状态和行动空间会导致强化学习算法很难在较短的时间内训练出一个满意的价值函数,为此,设计双智能体机制,以降低多技能项目调度过程中的状态行动空间.
3.2 双智能体机制
由式(11)可知在项目调度的MDP中,一步行动包含了活动选择和资源分配,为简化行动内容,设计双智能体,见图3.其中Agent1用以指导活动选择,即式(11)二元组的第1项,Agent2指导资源分配,即式(11)二元组的第2项.
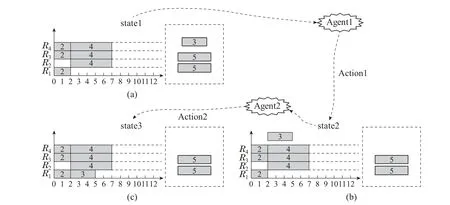
图3 双智能体机制Fig.3 Mechanism of two agents
3.2.1 Agent1状态及行动定义
在学习过程中,需要根据状态State1做出行动Action1.首先分析状态空间State1,针对式(10)三元组的第1项,由式(9)知和关于V互补,以代替表示State1不会丢失信息.更进一步地,在中,当前回合内行动所需要主要的信息是.为了尽可能保留信息,提取已排程活动的个数信息且用代替已排活动具体内容,式(10)中第1项便转化为{||,}.针对式(10)三元组的第2项,每次迭代内决策时点t已为确定值,内活动的开始时间对当前选择哪个活动加入排程这一行动的影响较小,因此将之省略.针对式(10)三元组的第3项,影响决策最主要的因素是当前剩余资源,用当前剩余资源数量表示.综上,状态空间State1可整合为
再分析行动空间Action1,Agent1只考虑活动选择,即从中选择一个活动j加入排程.其行动空间为
可以看出,状态空间State1虽然也是三元组的形式,但是其第1项和第2项都是仅含一个元素的数组,这大大降低了状态空间的规模.而Action1的规模则等于||,即当前可开始活动的数量.
3.2.2 Agent2状态及行动定义
在学习过程中,需要根据状态State2做出行动Action2.首先分析状态空间State2,在Agent1根据State1做出Action1后,达到新的状态State2,此时完备的状态需要明确已排活动所用资源及资源的使用时间,而Agent2 只负责为Agent1 所选活动分配资源,因此对Action2而言,最重要的状态信息是Action1所选择的活动j,故状态空间State2省略为
再分析行动Action2,行动内容是为活动j分配资源,行动的规模是在当前可用资源约束下,活动j可行的资源分配方案个数.
双智能体机制将调度中的每一步分为两个阶段,用State1和State2表示状态,既能降低状态的规模,也可以最大程度地保留调度过程中的主要信息.此外,Action1和Action2的规模分别等于内活动的数量和活动j可行的资源分配方案数量.行动规模为二者之和,而不再是二者之积,这降低了价值函数的维度.以图3为例,当t=2,={3},则State1={2,{3},1},Action1={3},State2={3},Action2={{R4}}.
3.3 价值函数
以项目工期最短为目标的MSPSP属于稀疏回报问题,本文的RLP算法不考虑即时奖励,使智能体尽可能地搜索全局最优解.以Deadline表示项目的工期期限,DS表示当前调度事件S的工期,最终回报为
强化Q学习算法采用一个表格直观地表示价值函数.本文参考这种形式,针对Agent1和Agent2,设计了表Qaa和Qar,其中Qaa对应State1,Action1,Qar对应State2,Action2,Q表的格式如图4所示.
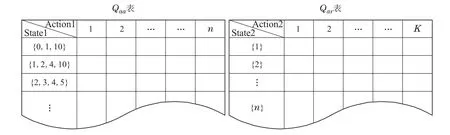
图4 Qaa表与Qar表Fig.4 Qaa and Qar
Qaa的行数可变,列数为n+1.第1列表示状态State1,第2到n+1列表示Action1.其中State1数组的第1个数值表示该状态下已排程活动数,最后一个数值表示该状态下可使用的资源数,中间数值表示当前可加入排程的活动.在调度过程中会不断产生新的状态State1,这些状态被不重复地列在Qaa表第1列,因此Qaa表的行是随着调度事件的产生不断增多的.而无论面临怎样的状态,Action1都是选择一个活动加入排程,即Action1的选择规模为活动数量n,因此Qaa表的列包括一个状态列及n个行动列.
Qar的行数为n,列数为K+1.第1列表示状态State2,第2到K+1列表示行动Action2.在调度过程中,State2是Action1所选的活动,规模为项目活动数量n,因此Qar表有n行.而所选活动所能使用的最大资源数量是项目中的资源总数K,即Qar表包括一个状态列和K个行动列.
3.4 算法流程
以PSGS 的角度看,以项目工期最短为目标的MSPSP,状态转移概率是已知且等于1的,然而其每一步的行动奖励是非即时且不确定的,即RLP算法是Model-free的,需要不断产生调度计划以供智能体采样,更新各状态行动的价值函数,基于此,算法流程包括两部分: 调度(采样)过程和学习过程,见图5所示.
3.4.1 调度过程
调度过程以PSGS为框架,随着决策时点t迭代,活动从依次被加入,直至完成调度.RLP采用Offpolicy的方式以ε的概率随机选择,以1-ε的概率贪婪选择,其中ε ∈[0,1].随机选择时,决策不参考任何经验信息,完全随机地选择活动和资源.贪婪选择时,根据Q表做出决策.其中Action1的贪婪决策过程为:根据当前调度进度,确定State1=state1,根据state1查询Qaa表决定Action1={j}.由于Qaa表中的状态空间初期并不完备,查询Qaa表时可能面临以下两种情况:
第1种情况,在Qaa表中可以找到与state1一致的状态,即该状态曾被采样过.此时只需要找到对应行,从该行中选择Q值最大的活动j进入state2即可.
第2种情况,在Qaa表中不存在与state1一致的状态,此时统计MDP 下一步各个状态的最优价值:v(state1′)=maxQ(state1′,action1′).而后根据v(state1′)选择最优价值最大的状态state1′,并将之与当前状态state1对比,选择一个在state1′中已排程而在state1中未排程的活动j作为Action1进入state2即可.采用这种方式的原因是: 即便Qaa表中尚未有与state1完全一致的状态,也可以通过将当前状态向最优状态靠近的方式,进行贪婪寻优.
Action2 则相对简单,由State2={j},查询Qar表中的第j行,根据当前可用资源剔除不可用资源,并根据活动j的技能需求,列出剩余资源的所有组合,从中选择Q值之和最大的资源组合分配给活动j,即可完成Action2进入最终状态state3.
3.4.2 学习过程
RLP的学习过程是智能体不断从调度计划中汲取经验更新价值函数的过程.它以MC-update法作为价值函数更新方式,即在调度计划生成的过程中暂停学习过程,在调度计划生成过程结束后,再根据调度计划的工期更新Q表.首先,分析Agent1,与调度过程相似,在更新Q值时可能面临以下两种情况:
第1种情况,在表中可以找到与state1一致的状态,此时直接更新对应Q值:
其中Nvisit是当前访问Q表中Qaa(state1,action1)位置的次数,Reward可根据式(16)获得.
第2种情况,找不到与state1一致的状态,则增加Qaa表的长度,将state1及以下Q值直接加入表中:
Agent2的Q表是完备的,在表中一定能找到与state2完全一致的状态,其更新方式为
3.5 算法优化
3.5.1 调度过程优化
整理资源的技能供给,由于在同一时刻每个资源只能被使用一次,尽管资源具备多技能,这些技能也是互斥的,因此有以下约束:
因此以xkli为未知数,只需判断方程组(20)-(23)是否有解,即可判断是否可行.然而该方程组是0-1型线性整数规划问题,属于NP难问题.对此本文提出技能归并法,算法伪代码见表1.

表1 算法1: 技能归并法Table 1 Algorithm 1: Skills conflation algorithm
算法第3行列出了要归并的z个技能的所有组合,第4-11行检验归并后的技能能否被当前资源满足,以supply和demand表示技能归并后的资源供给和活动需求.在过程中一旦出现供给不足则跳出所有循环,Feasb=0.若能通过所有组合的检验,则可行,Feasb=1.技能归并法的合理性来源于以下命题:
可以看出命题1Z为命题1的逆否命题,以下证明命题1Z.
证资源不满足有以下3种情况.
第1种情况是,资源的总数量不足,即
式(24)不等号左侧为可用资源总量,它等于归并所有技能(即z=L)为一个技能后,资源对所归并技能的供给supply.同理,不等号右侧等于归并L个技能后,活动对所归并技能的需求demand.因此式(24)等价于supply 第2种情况,资源总量足够,但是在某一个或几个技能上的数量不足,即 式(25)不等号左侧等于归并单个技能(即z=1)为一个技能后,资源对所归并技能的供给supply.同理,不等号右侧等于归并单个技能后活动的需求demand.因此式(25)等价于supply 第3种情况,可用资源总量足够,在每个技能上的资源量也足够,但是不存在可行的资源分配方案使所有技能需求被同时满足.出现这种情况的原因是资源技能的排他性,即一个资源虽然同时具备多项技能,但同一个时刻它只能执行一个技能.此时不可行的原因是技能之间存在抢夺资源的情况. 式(26)不等号左侧等于归并l和m为一个技能,资源对所归并技能的供给supply.不等号右侧等于归并l和m后活动的需求demand.因此式(26)等价于supply 综合以上3种情况和式(24)-(26),命题1Z得证,作为其逆否命题,命题1得证.证毕. 3.5.2 学习过程优化 针对Agent1,在每次迭代时,它需要根据当前访问次数更新Q值,为此,设计了辅助表Maa,其规模与Qaa表相同,Maa(state1,action1)中数值的含义是:当前访问Qaa(state1,action1)位置的次数Nvisit.同样地,针对Agent2,设计了辅助表Mar,其大小与Qar表相同,Mar(state2,action2)值的含义是: 当前访问Qar(state2,action2)位置的次数Nvisit. 为验证RLP算法,设计了单项目算例实验和项目算例集实验.相关程序用Matlab R2017a编写,测试平台为Windows 10操作系统,处理器为Intel(R)Core(T M)i7-6700 CPU@3.40 GHz. 4.1.1 单项目算例实验设计 在实验对象方面,采用如下项目案例.图6是一个包含30个实活动的项目,拥有10个多技能资源,4项技能,其网络图及活动信息标注在图中,资源技能矩阵RF=[0 1 0 0;1 1 0 1;0 1 0 0;0 0 1 1;1 0 0 0;0 1 0 1;0 1 0 1;0 1 1 0;0 1 0 0;1 0 0 0]. 图6 单项目算例项目网络图Fig.6 Network of the single project instance 在算法选择方面,对比算法为:随机调度算法、文献[7]和文献[9]基于规则的启发式算法,以及文献[11]的元启发式算法.在算法参数方面,设置文献[11]的元启发式算法以600 s为停止规则.RLP的相关参数设计如表2所示. 表2 算法参数设置Table 2 Parameters of the algorithm RLP 算法的停止条件有两个:Nepisode和Trun,满足其一便停止算法,输出结果.在生成调度计划阶段,选择行动时采取的是具有时变性的ε-greedy法,表中itr表示当前所产生的调度计划数量,随着算法的进行,ε由1逐渐趋向于0,即在算法前期,倾向于随机性地采取行动,来保证其探索性,而在算法后期则倾向于根据Q表贪婪地选择行动,来保证其利用性. 4.1.2 项目算例集实验设计 为验证算法的普适性,进一步设计了对大量不同的项目算例的实验.在实验对象方面,采用文献[9]中所设计的多技能项目算例集,其中共有算例360个,每个项目算例包含30个实活动,项目网络复杂度NC∈{1.5,1.8,2.1},需求因素RF∈{0.25,0.5,0.75,1},技能水平SL∈{0.4,0.6,0.8},项目参数含义参考文献[9].在算法选择及参数设置方面,对比算法为:随机调度算法、文献[7]和文献[9]基于规则的启发式算法,以及文献[11]的元启发式算法.其中应用文献[11]算法时,针对每个算例其运行时间设定为等于RLP算法求解该算例时的训练时间,以便于比较相同求解时间下算法的性能差异,算法的其他相关参数同表2. 4.2.1 单项目算例实验结果分析 利用RLP算法对以上算例进行求解,为展示其优化过程,统计了RLP算法的训练过程中,所采样的所有调度计划的平均工期(avgD(entire)),以及邻近20次调度计划的平均工期(avgD(nearby)),二者随训练次数的演变过程见图7所示.可以看出,除了在初期由于训练数据不足导致工期波动较大外,随着学习的进行,所求得的平均工期在不断下降,且在训练后期平均工期的波动也越来越小,表现出了稳定的学习进化能力.图8展示了通过RLP算法求得的一个最优项目调度计划的甘特图. 图7 平均工期随学习进度变化情况Fig.7 Changes of average makespan with learning progress 图8 单算例项目调度计划甘特图Fig.8 Gantt chart of the schedule of the single project 为进一步验证算法的有效性及稳定性,进行了100次独立重复试验.结果见表3,其中文献[7]和文献[9]的算法由于是基于规则的启发式算法,求解结果是固定的,不做重复试验.可以看出,相较于文献[7]和文献[9]的启发式算法,RLP算法能求得工期更短的调度计划,且求解时间也在可接受的范围内.相较于文献[11],比较均值可知,RLP算法有更大概率取得最优解,比较标准差可知,RLP算法具有更强的求解稳定性,且求解时间也低于元启发式算法. 表3 各算法运行100次求解结果统计Table 3 Statistics for 100 runs of each algorithm 4.2.2 项目算例集实验结果分析 针对算例集中的每个算例,每个算法进行一次求解,求解的结果展示在表4中.可以看出,相较于文献[7]和文献[9]中基于规则的调度算法,文献[11]及本文所提出的智能算法具有明显优势,这是因为前者是一种依据经验设计的固定策略下的启发式算法,能在一定程度上求得较优解,但其本身不具备寻优能力,而后者则可以通过迭代寻找较优解的特征,并对其不断优化,这也是其求解时间大于前者的原因.此外可以看出,RLP算法在求解算例集时的表现明显优于其他4种算法.这证明了单算例实验的实验结论具有一般性. 表4 各算法运行求解算例集的结果统计Table 4 Statistics for each algorithm to solve project__library 以上进行了针对单项目算例的重复试验和针对项目算例集的大规模实验,从实验结果可以看出:相较于传统基于规则的启发式算法,本文所提出的RLP算法寻优能力更强,但需要更多的求解时间;相较于文献[11]中的元启发式算法,当给予不同的求解时间时,表3显示RLP算法能更快求得最优解,且算法稳健性更高;当给予相同的求解时间时,表4显示RLP算法能求得更优的解. 项目调度问题作为NP难问题,一直以来其主要的求解手段都是启发式或元启发式算法,然而两种算法各有缺陷.强化学习算法作为机器学习领域重要的方法论之一,与项目调度问题具有较高的契合度,基于此,本文针对项目调度问题设计了基于强化学习的多技能项目调度算法RLP,求解以项目工期最短为目标的MSPSP. RLP算法首先将多技能项目调度过程建模为具有马尔科夫链性质的序贯决策过程,鉴于调度事件中状态行动空间规模过大,在解构调度进程中状态行动的基础上,设计了双智能体机制,通过状态整合和行动分解降低了状态行动空间的规模,使得算法可以用规模更小的Q表指导调度过程中的活动选择及资源分配.更进一步地,为了提高算法性能,设计了技能归并法以判断资源分配的合理性,通过复杂度分析发现,在技能数量较少的情况下,技能归并法能显著降低求解的时间复杂度.项目案例仿真实验结果表明,相较于其他算法,RLP求解性能更强,且稳定性更高.下一步的研究将考虑以机器学习的思想,求解复杂不确定环境下的项目调度问题,如多技能项目中的资源不确定、活动工期不确定等.4 实验与分析
4.1 实验设计

4.2 实验结果分析
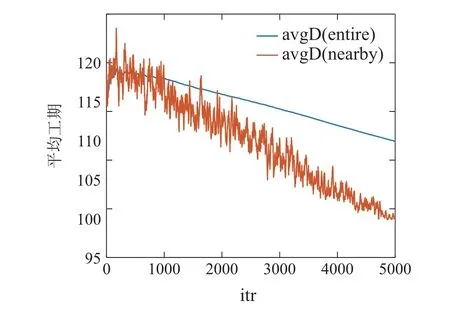
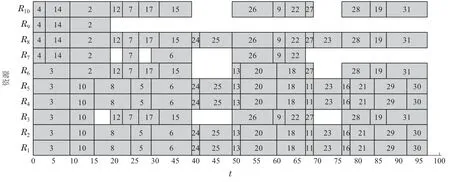

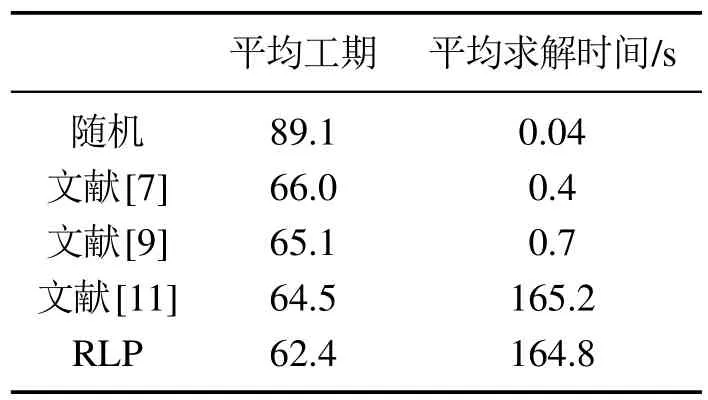
5 结束语
