透射光谱线性空间核学习建模求解多组分浓度
2024-05-11宋江婷金福江周丽春
宋江婷,金福江,周丽春
(华侨大学机电及自动化学院,福建厦门 361021)
1 引言
溶液组分浓度的测量常采用基于Lambert-Beer定律的分光光度计法[1-3],此方法对于中低浓度、浅颜色的溶液有很好的测量效果,但对于高浓度、深颜色的溶液有较大的测量误差[4-6],其原因为Lambert-Beer定律仅为经验公式,缺乏相关的机理研究.
本文前期将入射光看作光量子,假设单组分溶液是由结构完全相同的大量的分子组成,并将其视为分子势垒,入射光透过单组分溶液视为光量子波函数在分子势垒作用下的演变的过程.通过求解薛定谔方程得到透射光波函数及透射光的光谱函数,最终得到了单组分溶液组分浓度的量子隧穿软测量模型[7].
多组分溶液是指溶质是多种结构、不同数量的物质分子组成的体系,多组分浓度同时测定需要同时测量出溶液中每种组分的浓度.多组分浓度测定通常采用基于经验或实验模型[8-10],依据Lambert-Beer定律建立线性方程组求解各组分的浓度.为提高测量精度,又采用一阶导数光谱法[11]、偏最小二乘法[12]、引入光谱峰面积[13]等技术.这些方法对单组分、低浓度溶液组分浓度的测量有较好的效果,但对于提高多组分浓度同时测定的测量精度并不显著.文献[14]提出了一个多组分染液染料浓度的二次型测量模型,应用该模型大大提高了多组分染液染料浓度的测量精度,但该模型仅对特定的几种活性染料有较好的测量结果,且建模需大量的实验,工作量大,成本高,建模周期长.
另外,还可以应用量子隧穿的机理,将入射光看作光量子,假设多组分溶液是由多种结构相同、大量的分子组成,也将其势垒视为多个分子势垒组成,入射光透过溶液视为光量子波函数与多分子势垒作用下演变过程,通过求解薛定谔方程组得到透射光波函数及光谱函数,最终得到了多组分溶液组分浓度的量子隧穿测量模型.但该方法随着分子种类及分子数量的增加,薛定谔方程中的变量数、方程的个数也随之增多,求解面临巨大困难.
本文将多组分溶液抽象成势垒线性空间,多组分溶液的透射光谱看成是以单分子的透射光谱为基函数、单组分分子数量占比为坐标的线性组合,得到透射光光谱函数向量空间,把光量子透过多组分势垒后光谱函数转化为单组分透射光谱函数的叠加,建立以多组分透射光谱为输出,以各单组分溶液组分浓度测量模型为核函数,单组分浓度为权系数为输入的多组分浓度测量模型,运用最小二乘法完成多组分浓度的求解.
2 多组分透射光谱线性空间
原子中的电子因能级分布而形成原子轨道,原子轨道是波函数[15],由原子轨道叠加而成的分子轨道也同样是波函数,一般称为势函数.光束照射分子的过程可看作是光量子波函数与分子势函数相互作用的过程.
2.1 多组分分子势函数矩阵
设多组分体系由m种、每种数量为n的单分子组成(m,n ∈N+),各类分子随机分布于体系中,多组分分子势函数VM可用m行n列分子势函数组成的矩阵表示,m行为m种分子,n为每行有n个相同或不同种类的分子,具体表示为
当m,n相等时,VM为m阶方阵.
2.2 多组分势函数矩阵的线性变换
定理1能够找到一个矩阵P,使得多组分分子势函数矩阵VM可以转化为各单组分分子势函数块矩阵Ji组成的对角阵.
证对于m阶多组分分子势函数矩阵VM,存在一个Jordan标准形与之相似[16-17],这个Jordan标准形除去其中Jordan块的排列次序外,是被VM唯一确定的.
同种分子具有相同的特征值,Ji(i=1,2,···,r)是由同种分子势函数组成的Jordan块.在多组分溶液中,每个分子的位置不同,每个特征值对应的特征向量线性无关,多组分分子势函数矩阵为满秩矩阵,所以存在一个可逆矩阵P,使得
根据文献[18]中的方法可求出非奇异矩阵P,由此多组分分子势函数矩阵可转换成各单组分分子势函数块矩阵Ji组成的对角阵J,光量子隧穿多组分体系势垒的薛定谔方程即可简化为光量子隧穿各单组分体系势垒的薛定谔方程组,即
其中:ni(i=1,2,···,m)为每种单组分分子的数量,Vsi(i=1,2,···,m)为各单组分分子势函数.
当已知各单组分分子势函数Vsi(i=1,2,···,m)时,由式
可得到多组分分子势函数矩阵VM.式(4)(6)说明,多组分分子势函数是单组分分子势函数为基函数,以分子位置为坐标的线性空间.
2.3 多组分分子透射光谱线性空间
由式(5)得到m个单组分透射波函数的解ψTi(i=1,2,···,m),利用可逆矩阵P及式(6)可得到多组分透射波矩阵ψT,即
其中ψti(i=1,2,···,m)是每种单分子的透射波函数,单组分中每个单分子透射波函数ψti(i=1,2,···,m)相同,由此得到定理2.
定理2 若单波长的透射光按波长大小依次排列则形成透射光谱,光谱函数表示为ψT(λ).多组分透射光谱空间是由各个单组分的分子光谱为基函数,每个组分所占比例为坐标的线性组合.
由透射光谱可得到溶液的吸光度,多组分溶液的吸光度A(λ)与各单组分吸光度Asi(λ)、各单分子吸光度Ai(λ)(i=1,2,···,m)之间的关系为
3 多组分透射光线性空间的组分浓度模型的核学习建模
多核学习(multiple kernel learning)可以看作是多任务学习(multi-task learning),也可以看作是迁移学习(transfer learning),每个核函数表示一个子任务,多核学习能够针对场景来组合各个核函数以获取更好的结果[19-21],各子任务对当前学习任务的贡献由其权重表示.在多核学习问题中,实际上就是对基核函数与核函数组合系数的选择问题,如何学习出一个合适的核函数组合系数,便是多核学习方法的本质所在.
利用核函数可以大大简化计算,但如何针对具体的问题设计出最适当的核函数却是一个难点.实际上,经常采用的方法是直接定义核函数,从而隐含地定义了特征空间.在多核学习中,比较常用的是多个单核函数的凸组合.在本文中,定义单组分体系的量子隧穿吸光度模型为核函数,因各单组分体系的权重均为非负数,所以多组分体系吸光度是多个单核函数的凸组合,即
其中:i(i=1,2,···,m)为基核数目;αi为第i个基核函数对应的权值;Ai(λ)为基核;ε为模型噪声,服从正态分布(0,σ2).本文使用多核最小二乘法方法将求解式(9)转化为求解以下最小值优化问题,即
光波λ从400 nm开始测量至700 nm,可得到n组数据A(λj)(j=1,2,···,n).
将有约束的目标函数转换成无约束的拉格朗日目标函数,有
其中β是受约束的拉格朗日乘子.
对式(11)的α和β分别求偏导,有
进而得到联立的正规方程
A400,A405,···,A700是指在波长为400 nm,405 nm,···,700 nm处的吸光度测量值.
式(13)正规方程可以写为
因X矩阵是由不同种类的单组分体系吸收光谱组成,所以矩阵为满秩矩阵,XTX为式(14a),求解可有
将式(15)代入式(14b),此时αi=(i=1,2,···,m)即为各项最优值.
4 实例验证
本次验证选用3种单组分活性染料进行混合溶液的验证.已知单组分活性染料红B-3BF 的分子式为C9H13O6NS2,分子相对质量为295;活性染料黄B-3RD 的分子式为C28H20O16ClN9Na4S5,相对分子质量为1026;活性染料深蓝B-2GLN 的分子式为C33H9ClNa5O19S6,分子相对质量1192.
在文献[22]中已完成活性染料红B-3BF、活性染料黄B-3RD、活性染料深蓝B-2GLN这3种单组分染料分子的光谱函数建模A1(λ),A2(λ)和A3(λ).
3种染料组成的多组分染料染液的理论光谱函数模型为
现用此3 种单分子染料调配成质量浓度分别为0.003,0.01,0.045(g/L),摩尔浓度归一化后的配比系数αi(i=1,2,3)分别为0.179,0.161,0.66 的多组分染料染液,测得混合染料染液的光谱曲线为图1中的蓝色曲线;将配比系数αi(i=1,2,3)代入理论光谱函数模型,得到模型的预测曲线为图1中的橙色曲线.观察两条曲线发现,预测曲线与实验曲线贴合较好,整体走势一致,说明本理论模型具有可行性.
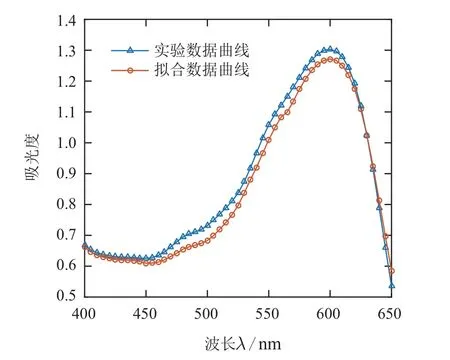
图1 多组分染料染液吸收光谱曲线Fig.1 Absorption spectrum of multicomponent dye solution
这3种染料继续调配成另外一组质量浓度分别为0.015,0.035,0.001(g/L),摩尔浓度归一化后的配比系数αi(i=1,2,3)分别为0.557,0.351,0.092的多组分染料染液,实验测量其吸收光谱曲线如图2中的橙色曲线.

图2 多组分染料染液吸收光谱图Fig.2 Absorption spectrum of multicomponent dye solution
根据式(16)多组分染料染液的理论光谱函数模型及核学习方法得到3种染料的配比系数(i=1,2,3)分别为0.586,0.301,0.113,将αi(i=1,2,3)代入模型(16)中得到预测光谱曲线,即图2中的蓝色曲线.虽然实验曲线与预测曲线没有完全重合,但整体趋势一致.实际配比系数αi(i=1,2,3)和理论配比系数(i=1,2,3)的总体标准差为
预测的误差与现有方法的误差基本相同,但本文主要目的是建立理论模型、验证模型的正确性,因此验证结果证明了理论的正确性.不仅如此,将单组分染料的量子隧穿浓度测量模型看做核函数,采用加权线性组合的方法将多个核融合建立多组分透射光线性空间的组分浓度模型,解决了多组分分子量子隧穿浓度测量模型的复杂程度,简化了计算过程.融合后的核函数兼有各个核的特点,能够很好的适应多组分分子中的异构点.此外,因多核是由多个不同的核函数融合而成,在实际应用中,可以灵活选用或更换核函数以适应不同的需求,以此实现了无限配方问题,避免了传统方法建模时对所有组分进行的大量实验,大大节约了成本与时间.
5 结论
本文分析了基于Lambert-Beer定律的多组分浓度同时测定法误差的原因,提出了多组分透射光线性空间的组分浓度模型的核学习建模方法,并验证了模型的有效性,最终得出结论如下:
1) 理论上证明了光量子隧穿多组分分子的透射光波为各单组分透射光波的线性叠加,多组分透射光波函数是以单分子透射光波函数为基函数、单组分分子数量占比为坐标的波函数线性空间.
2) 首次将单组分的量子隧穿浓度模型看作是核函数,建立了多核学习的多组分浓度测定模型.模型融合了各个核的优点,有效地预测了多组分体系浓度,达到了最优预测值.
3) 多组分透射光线性空间是单组分体系透射光的线性叠加这一结论说明,若用光量子隧穿法同时测定多组分浓度,不必再求解复杂的薛定谔方程组,只需求解各单组分体系组成的薛定谔方程组即可,大大简化了计算过程;同时,此方法解决了文献[14]的问题,对于由多种单组分调配多组分溶液,不必全部重新建模,只需更改所需的单组分溶液即可,大大节约了工作量与实验成本,完全实现了无限配方问题.
