基于超图正则化的域适应偏最小二乘多工况软测量模型
2024-05-11霍海丹阎高伟任密蜂
霍海丹,阎高伟,王 芳,任密蜂,程 兰,李 荣
(太原理工大学电气与动力工程学院,山西太原 030024)
1 引言
流程工业是国民经济的重要支柱产业,其生产过程涉及复杂的物理化学反应,难以用数学模型精确描述,且受测量成本和物理条件等因素的限制,一些关键参数和产品质量变量难以通过传感器实现实时直接测量.基于数据驱动的软测量技术,是解决上述问题的有效方法之一[1-2].然而在实际工业过程中,由于原料来源多样、成分复杂以及生产条件多变,导致工况波动频繁,造成数据呈现多模态特性,不同工况数据难以满足独立同分布的假设[3].因此,建立在数据同分布假设基础上的传统软测量模型在工况发生改变时,其预测精度将显著下降[4].
目前,针对多工况软测量建模问题,常见的建模策略是采用自适应学习方法.主要包括即时学习(just in time learning,JITL)、移动窗口(moving-window,MW)和集成学习(ensemble learning,EL)等.文献[5]提出与JITL相结合的直推式MW学习器,在域适应极限学习机的基础上将JITL建立的局部模型的预测值视为伪标签,对MW 模型进行校正.该方法中MW 仅使用确定数量的最新样本更新模型,以应对数据漂移的缓慢变化.文献[6]针对MW在适应突变和重复漂移时表现出的延迟问题,提出了MWadp-JITL 模型,将自适应MW 模型和JITL 模型相结合,利用相关向量机建模进行预测.但是当数据分布存在较大差异时,即时学习难以选择出符合当前工况模态特性的有效样本,且难以确定训练样本的权重.最重要的一点是,大多数工作建模的背景需要测试集的标记数据或者假设在一定时间后可以获得真值,这在实际工业过程中有时很难满足.
域适应[7-8](domain adaptation,DA)方法,通过将源域(历史工况)学习到的知识迁移到目标域(当前工况),来减小不同工况之间数据的分布差异,为解决工业中多工况下软测量问题提供了思路[9].特别是近年来,有学者将基于特征表示[10]的域适应方法作为正则项对历史工况预测模型进行约束,使得模型能够适应工况变化,提高模型的预测精度[11].文献[12]提出了基于无监督迁移学习的目标检测(unsupervised transfer learning based target detection,UTLD)方法,该方法通过判别流形嵌入学习和迁移正则化对知识进行迁移,使得目标域的每个样本可以由源域的相邻样本线性重构[13-14].在此基础上,文献[15]对重构矩阵施加低秩约束,来保持全局子空间结构,并利用稀疏约束,在特征层保持数据的局部几何结构.但是上述方法针对的是分类任务,对于回归任务而言,连续标签无法进行与类别标签相同的重构过程,因此上述模型无法直接应用于软测量领域.为此,文献[16-17]提出一种域不变迭代偏最小二乘(domain-invariant iterative partial least squares,DIPALS)方法,将协方差对齐项作为偏最小二乘(PLS)的域适应正则化项,在寻找历史工况潜变量空间的同时实现历史工况和当前工况数据的分布适配.DIPALS提供了一种利用域适应方法解决回归问题的框架,但是忽略了域适应过程易对过程数据结构造成破坏的问题.鉴于几何结构信息也是数据的一个重要属性,因此,如何使模型既考虑标签的解释信息,又避免域适应过程对原始数据结构的破坏是建立跨工况软测量模型的关键.
综上所述,为解决变工况下数据分布变化导致软测量模型恶化的问题,本文认为建立跨工况的软测量模型需要注意如下3点: 1)降低数据分布差异,尽量使数据在分布上符合统计机器学习建模的基础假设;2)降低分布差异的过程不能破坏数据内蕴含的结构关系,或者在数据变换过程中应尽可能保持其结构关系;3)需要保持数据对标签的解释性.上述3个出发点中,第1点和第3点可以分别利用域适应的思想和偏最小二乘的框架加以解决.但是第2点在现有理论和技术的基础上需要重点考虑.通常,原始空间数据的内在结构在投影过程中可以利用图拉普拉斯正则化来约束使其保持不变[18].例如,时间近邻拉普拉斯正则化多工况回归模型[19](multi-conditions soft sensor regression model based on time-nearest neighbor Laplacian regu-larization,TNN-LR-MR)在DIPALS基础上引入C近邻拉普拉斯正则化项,保留了样本的局部结构,提高了模型的预测性能.但是上述普通的拉普拉斯图刻画的是点与点之间的成对关系,而回归任务中需要考虑数据的平滑性、连续性以及相关关系,因此,数据之间的关系应该比简单的成对关系更复杂.如果将这种复杂的关系利用普通图压缩成成对的关系,将不可避免地导致丢失部分对回归任务有价值的信息.
超图为刻画高阶结构关系提供了一种选择.文献[20]基于典型相关分析,通过超图正则化进一步考虑了高阶标签结构信息,提出了一个新的多标签分类框架.文献[21]通过类别伪标签建立超图,保留特征和标签之间的映射关系,提高了无监督软测量模型的性能.但是,上述方法利用类别标签构造超边,挖掘特征的高阶信息,因此,对于不存在类别标签的回归任务,如何利用连续标签构造超边是研究的难点.文献[22]基于相同特征超边中的蛋白质具有相似潜在编码,并且相似的潜在编码产生相似注释的假设,来构造模糊超图刻画特征空间和标签空间的内在关系.受此启发,本文利用时间C近邻线性回归方法构建超图来捕获原始特征空间样本的高阶信息.
基于上述分析,本文提出了基于超图正则化的域适应偏最小二乘回归(domain adaptation partial least squares regression based on hypergraph regularization,HD-PLSR)模型.如图所示,图1(a)-(b)中二维坐标表示原始数据空间的坐标,图1(c)-(d)中二维坐标表示潜变量空间的坐标;图1(b)表示原始空间历史工况和当前工况数据;首先,图1(a)利用时间C近邻线性回归刻画数据的相关关系建立超图,挖掘历史工况和当前工况原始数据的复杂高阶关系,投影在图1(c)潜变量空间中,保持数据结构关系以约束潜变量空间的求解;然后,在图1(d)潜变量空间中,利用历史工况的样本对当前工况样本进行重构,作为域适应正则化约束使得数据分布对齐;最后,图1(e)将上述正则化项嵌入偏最小二乘框架中,增强潜变量对标签的解释性.在两个约束项下获得投影阵后建立模型实现对历史工况数据的预测.

图1 超图正则化的域适应偏最小二乘软测量算法示意图Fig.1 Schematic diagram of the domain adaptation partial least squares soft-sensing algorithm for hypergraph regularization
2 相关理论
2.1 符号定义
2.2 问题描述
无监督域适应回归模型的目标为通过寻找一个映射h:Rm →R,使得目标域上的预测损失期望最小[17],即
目标域预测损失期望上界为
其中:g:Rm →Rd,f:RL →R,m是原始空间的维度,d是潜变量空间的维度,h=f ◦g是f和g的复合函数.由g函数实现从原始空间到潜变量空间的映射,f函数实现从潜变量空间到标签空间的映射.式(2)第1项为源域损失期望,第2项dH(DS,DT)为域间差异,第3项为最优联合泛化误差.
在本文框架中,假设投影矩阵均为线性算子g(X)=T=XW,W ∈Rm×d,f(T)=T c,c ∈Rd×1,W为原始空间到潜变量空间的投影矩阵,c为潜变量和标签的回归系数.式(2)第1项由偏最小二乘(PLS)模型实现源域损失最小,第2项由基于特征表示和基于图准则的领域分布差异的方法表示.第3项通常忽略不计[23].所以本文重点通过最小化前两项来降低目标域的预测误差.
2.3 偏最小二乘回归模型
PLS是一种常见的多元回归分析方法,因其在克服变量多重相关性中的显著优势,已被广泛应用于软测量领域.PLS通过寻找与标签相关性最大的特征潜变量,来获取投影向量实现维度约简.以历史工况数据建模为例,标准PLS的目标函数为
其中:wi为第i个潜变量的投影向量,d为潜变量的个数.本文选取非线性迭代偏最小二乘[24](nonlinear iterative partial least squares,NIPALS)对式(3)进行求解,具体步骤包含4步,即: 初始化、映射、回归和直交补.其中,求解潜变量映射的目标函数为
本节旨在强调NIPALS方法每次迭代过程中求解映射向量的思路,具体计算过程可以参考文献[24].
2.4 基于特征表示的域适应正则化
针对多工况条件下过程数据存在分布差异导致模型预测精度下降的问题,本文引入了基于特征表示的域适应正则化项来寻找两个工况的公共潜变量空间,在该子空间中利用历史工况数据对当前工况数据进行重构,增强两个工况间的相关性,从而实现工况间数据分布对齐.另外,对重构矩阵施加低秩稀疏约束,保持数据的全局子空间结构和局部几何结构,并使用一个稀疏矩阵E来补偿噪声数据.该问题可以表示为
2.5 基于连续标签的超图构建
本文通过基于特征表示的域适应正则化项,增强两个工况数据之间的相关性来减小工况间的数据分布差异,但是从原始空间到潜变量空间的投影会破坏原始空间数据的结构关系.因此,引入超图建立原始数据高阶结构关系,形成超图拉普拉斯正则化项嵌入到目标函数中,在求解过程中和域适应正则化项共同优化潜变量空间,实现域适应过程中保持原始数据结构的目标.
超图的定义为G=(V,E,S),它由顶点集V={v1,···,vN}、超边集E={e1,···,ek}和超边集的权重矩阵S组成.本文将所有的样本X作为超图的顶点集V,超边和关联矩阵可以采用稀疏线性回归的方法[26]构建,该方法解决了回归问题中因为缺少类别标签难以确定超边的问题,目标式为
其中:Ai=(v1,v2,···,vi-1,vi+1,···,vN)∈Rm×N-1表示顶点V中除第i个样本以外的所有样本;αi∈RN-1是其他样本对第i个样本影响程度的系数向量;γ是正则化参数,用于约束解的稀疏性.
在式(7)中引入稀疏约束保持数据的局部近邻关系,但是其结果容易受正则化参数γ的影响,同时模型训练时间长,本文将在第4.4节中对此问题进行具体探讨.文献[19]提出时间近邻假设: 对于过程数据,数据点只与时间点前后的C个数据产生近邻关系.因此,本文利用该文献的时间C近邻方法获得每个样本的近邻样本,代替稀疏约束.这样既保持数据的序列结构,又大幅度减少模型训练时间以满足工业实时性要求.最终根据式(8)确定超边,具体求解可以归结为3步.
第1步利用文献[19]提出的时间C近邻方法获得每个样本的近邻样本;
第2步利用式(9)计算出每个样本的线性回归系数.将目标式(8)矩阵化:
第3步本文认为回归系数大于0的样本和重构样本具有几何意义上的相似性,可视为属于同一个超边.即超边ei由第i个样本和系数向量αi中相应元素为正的其他样本组成.
利用式(8)建立样本的超边时,由于对历史工况和当前工况的每个样本特征都进行了线性回归,因此会产生ns+nt个超边.最终建立超图关联矩阵为H=.归一化超图拉普拉斯矩阵表示为[20]
其中Dv和De为顶点度和超边度的对角矩阵.
超图正则化项被定义为[27]
其中f被看作超图的嵌入,可以通过线性变换W学习低维嵌入.为了尽可能的使数据在新的表示空间中保持平滑,需要最小化Ω(f),可以表示为[27]
3 算法模型及优化
为减少历史工况和当前工况之间的数据分布差异,同时避免域适应过程中破坏原始空间特征高阶结构关系.在NIPALS中引入基于特征表示的域适应正则项和超图拉普拉斯正则项.将式(4)(6)(13)结合在一起,构建HD-PLSR模型目标函数为
其中:wi为迭代过程中的投影向量;γ,η和σ分别为域适应对齐正则项与超图拉普拉斯正则项的正则化系数.
从式(14)的模型中可以看出,该模型涉及两个变量wi和Z的最优解.由于目标函数是非凸优化问题,采用非精确增广拉格朗日乘子方法(inexact augmented Lagrange multiplier,IALM)[25]求解该模型.为了使得目标函数可分离求解,引入辅助变量Z1和Z2将问题等价为
拉格朗日乘子方法(ALM)方法通常用来解决核正则化优化问题[28],式(15)表示为
其中:A1,A2,A3为拉格朗日乘子,惩罚系数µ>0.该问题可以用交替乘子法进行求解.主要步骤如下所示:
步骤1更新wi,只保留含wi的式子,通过拉格朗日乘子法可得到其闭式解,即
步骤2更新Z,只保留含Z的式子,对其求导得到闭式解
步骤3更新Z1,可通过下式求解[29]:
其中:ϑλ(X)=USλ(Σ)VT是关于奇异值λ的阈值算 子,Sλ(Σij)=sgnΣijmax(0,|Σij-λ|)是软阈值算子,X=UΣVT是X的奇异值分解.
步骤4更新Z2,根据收缩算子[30]求解,得到闭合形式解
步骤5更新E,闭合形式解如下:
式(20)-(21)中,shinrk(x,a)=sgn max(|x|-a,0).
步骤6更新拉格朗日乘子
步骤1到步骤6迭代收敛后,获得投影向量wi,对应于NIPALS 算法求解映射向量的步骤,之后带入NIPALS框架完成剩余步骤.总体算法流程如算法1(见表1)所示.

表1 算法1:超图正则化域适应偏最小二乘多工况软测量算法伪代码Table 1 Algorithm 1: The hypergraph regularization domain adapts to the partial least squares multi-case,soft-sensing algorithm pseudo-code
4 实验结果及分析
为验证本文算法的有效性,选取三聚氰胺(Melamine)数据集[17]、玉米(Corn)样品近红外线光谱数据集[17]和田纳西伊斯曼(Tennessee Eastman,TE)仿真数据集[21]进行实验.对比实验包括基模型PLSR、自适应滑动窗口偏最小二乘(moving window partial least square,MWPLS)、基于特征表示的协方差对齐[10](correlation alignment,CORAL)算法和测地线流式核[31](geodesic flow kernel,GFK)算法,以及基于PLSR框架的DIPALS算法和TNN-LR-MR算法.需注意的是,上述对比方法所涉及的模型参数均采用交替更新策略进行寻优.
为了评价算法的预测性能,采用均方根误差(root mean square error,RMSE)作为模型预测性能的评价指标,其计算公式如下:
其中:N为测试样本的数量,yi为第i个样本的真实值,为第i个样本的估计值.
4.1 数据集与实验结果
三聚氰胺数据集[17]来自于批量聚合过程,记录了三聚氰胺树脂在不同聚合度下吸收不同波段的近红外(near infrared,NIR)光谱,常应用于检验跨工况软测量算法的性能.在实验中本文将两个不同波段(5546~6254 mm和6596~6975 mm)的光谱特征作为辅助变量,将聚合度相关的浊点温度作为关键变量对其进行预测.该数据集共包括4种不同聚合度下三聚氰胺树脂的相关数据,将其视为4个不同的工况,每次选择一个工况作为历史工况,其余3个作为当前工况,用于完成跨工况建模与预测实验.
实验结果如表2所示.与基线模型PLSR相比,除GFK模型的预测结果较差以外,其他域适应方法都有所改善.CORAL方法利用对齐后的特征建立回归模型,在分布对齐的过程中未考虑标签的解释性,改善幅度较小.而DIPALS,TNN-LR-MR,HD-PLSR模型结合域适应项和源域损失最小建立目标函数,求解过程中基于NIPALS框架考虑了标签的解释性,对模型预测结果的改善相对比较大.MWPLS模型结果虽然存在个别结果改善比较大的情况,但大部分结果较差而且恶化程度大.相比之下本文提出的HD-PLSR模型的预测精度整体上改善比较显著.
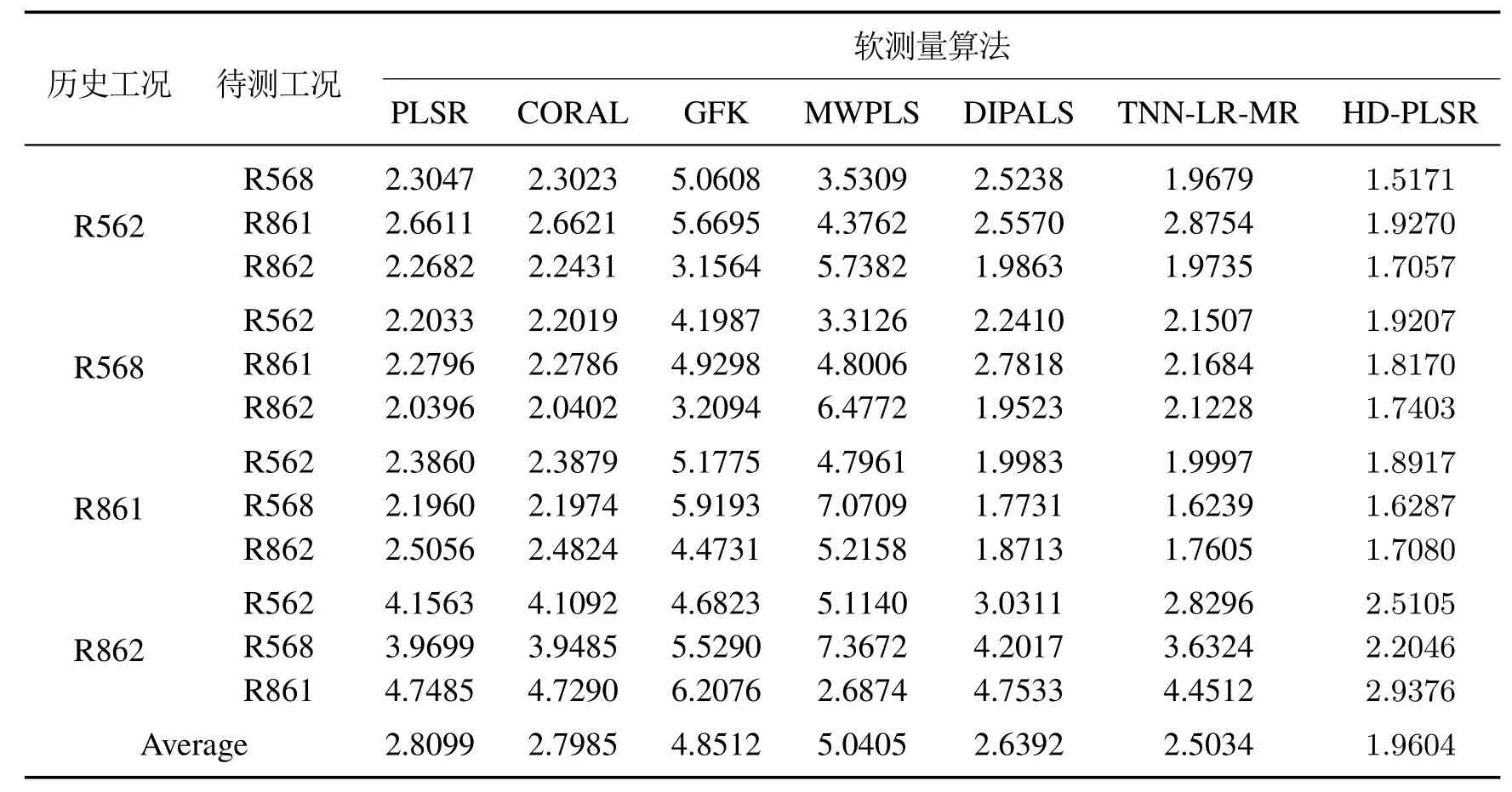
表2 Melamine数据集不同工况之间对比实验的均方根误差Table 2 The RMSE of the comparative experiment between different conditions of the melamine data set
TE化工仿真数据是软测量领域常用的工业过程数据.TE过程主要包括5个主要单元,共有12个操纵变量、22个过程测量变量、19个成分测量变量和5种反应物A,B,C,D和E.本文选择22个过程变量和11个控制变量作为辅助变量,对关键变量反应物A进行预测.根据生产需求确定反应器液位参数和改变反应器压力产生多工况特性.分别以工况1-工况4为历史工况,其他工况作为当前工况,完成跨工况预测实验.
实验结果如图2所示.图2(a)为所有不同对比方法的箱线图,其中箱体表示误差结果的集中范围,箱子中的横线表示数据的平均水平.从图中可以看出本文方法优于其他的对比方法.将误差均值可视化,如图2(b)所示,可以看出本文方法的平均误差为0.445,与次优方法DIPALS相比,误差降低了13.5%,与基模型PLSR相比降低了34.1%,进一步说明了本文提出的模型比其他的对比模型更稳定.
Corn数据集一般用于进行仪器校准,其包含了来自3 台不同的光谱仪上(m5,mp5,mp6) 测量的80 个玉米样本的NIR 光谱数据,波长范围为1100 nm~2498 nm,间隔为2 nm,用于对样本的水分(moisture)、油(oil)、蛋白质(protein)、淀粉(starch)的含量进行预测.由于不同光谱仪存在差异,因此,可以将其视为不同工况之间的回归迁移问题.分别用来自一个光谱仪的数据作为历史工况,其余两个作为当前工况完成迁移实验.
实验结果如图3所示,图3(a)为Corn数据集预测误差箱线图,可以看出本文方法的预测误差最低.图3(b)为误差均值和标准差,可以看出与基模型PLSR相比,本文HD-PLSR 模型的预测精度最高,GFK 模型和MWPLS模型预测误差增大,CORAL模型和PLSR模型的结果相近,改善不大,其他的模型都有所改善,精度提升了29.3%左右,但是本文模型提升约34%,表现更佳.
4.2 实验结果分析
从3个工业数据集的实验结果可知,域适应方法(CORAL,GFK)将历史工况和当前工况数据分布对齐后再建立回归模型,与传统软测量方法PLSR相比,由于在数据分布对齐过程中未考虑数据对标签的解释性,部分实验预测误差增大,出现负迁移情况.自适应MWPLS方法,在TE数据集和Melamine数据集上有所改善,但是改善程度不大,尤其在Corn数据集上出现恶化的情况,这是由于自适应MWPLS方法假设当前工况中的标签在一段时间后可以获得,通过获得的标签对模型进行更新以减少概念漂移,但是这与本文的背景不一致.为将其与本文方法进行比较,利用伪标签来更新模型,由于它受伪标签不确定性影响,所以会出现部分预测结果恶化的情况.DIPALS方法在NIPALS框架下引入协方差域适应正则化项,和PLSR相比有所改善,但是其忽略了数据的几何结构,与本文HD-PLSR模型相比结果较差.TNN-LR-MR在NIPALS框架下引入协方差域适应项和普通图正则化项,部分结果没有改善,是因为普通图只能建立样本的两两对应关系,忽略了数据的高阶关系.本文HD-PLSR模型利用超图正则化后实验结果有较大改善,进一步验证了本文方法的有效性和泛化性.
4.3 正则化项性能分析
为分析目标函数中各正则项的作用,将传统建模方法PLSR 与式(24)-(26)3个模型和本文的HD-PLSR模型作对比.将只引入域适应方法而没有流形正则化的模型记为PLSR+DR,其目标函数如式(24)所示:
没有域适应正则化项只引入普通图正则化项的模型记为PLSR+MR(Laplace),目标函数如式(25)所示:
没有域适应正则化项只引入超图正则项的模型记为PLSR+MR(Hypergraph),目标函数如式(26)所示:
上述对比方法在3个数据集上的预测误差的均值如表3所示,从表中可以看出本文建立的HD-PLSR模型同时考虑域适应正则化项和流形正则化项时预测效果最佳.将其可视化,部分实验结果如图4所示.

表3 不同正则化项在3个数据集上的RMSE均值结果对比Table 3 Comparison of the RMSE mean results of each regularization term on the three datasets
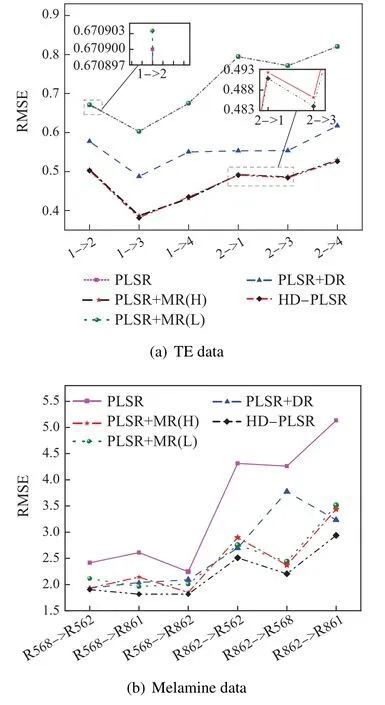
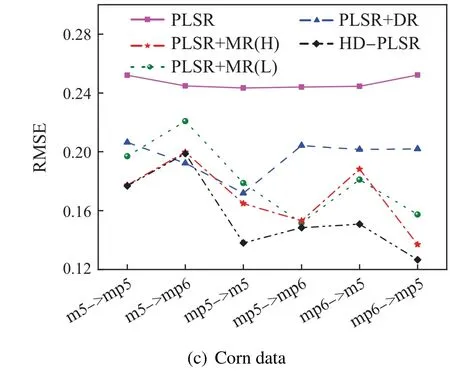
图4 3个数据集上不同预测方法的RMSE结果对比Fig.4 Comparison of RMSE results of different forecasting methods on three datasets
本文中域适应正则化项的引入是为了减小历史工况和当前工况数据的分布差异对模型预测精度的影响.以Melamine数据集为例,利用边际分布曲线图来体现不同方法下历史工况与当前工况的潜变量分布差异,如图5所示.其由散点图和核密度估计曲线图构成,横纵坐标分别表示不同模型第1个和第2个潜变量.

图5 潜变量空间中源域和目标域边际分布Fig.5 Marginal distributions of source and target domains in latent variable space
PLSR+DR模型引入了基于特征表示的域适应正则项.从图5(a)PLSR模型的核密度分布曲线图可以看出,该模型在历史工况和当前工况上都存在数据分布差异,引入域适应的PLSR+DR模型中潜变量分布差异减小,进一步说明引入域适应项可以减小数据分布差异,并改善模型的预测性能.但是PLSR+DR模型存在一定的缺陷,两个潜变量的分布都出现了双峰的现象,即两极分化增强,同时散点图分布密集,表明在该方向下所包含的特征信息较少.PLSR+MR(Laplace)模型引入普通图正则化项保持了潜变量空间的数据几何结构.通过图5(b)和图5(c)对PLSR+MR 模型和PLSR+DR模型做对比,从核密度分布角度出发,在PLSR+MR模型下,两域的分布差异较大;从散点图角度出发,两个模型的分布相近,但是都缺乏对特征信息的解释性.因此,考虑将域适应项和超图正则化项同时训练,建立本文的HD-PLSR模型.从图5(d)图可以看出,与PLSR模型相比,本文方法中,不同工况数据的核密度分布差异减小,同时从散点图可以看出本文方法能够实现不同工况数据的边际分布对齐.相比于PLSR+DR模型,本文方法的核密度分布呈现从双峰向单峰的转变,两级分化现象减弱,同时散点分布在保持分布对齐的同时分布疏散,对特征信息的解释性增强,因此,本文方法的预测精度更高,与表2的结果保持一致.
4.4 超图构造分析
软测量模型需要较强的实时性.在第2.5节中,利用式(7)所示的稀疏线性回归方法建立每个超边的时间复杂度为O(r3+(ns+nt)2),其中r是回归系数α中非零系数的数目.该方法建立超图关联矩阵所需时间长,无法满足工业实时性需求.考虑到实际工业过程中,采集的数据往往具有时间序列结构的特性,并且数据量大.本文选用如式(8)所示的时间C近邻回归方法建立原始数据的超图.该方法所构建的超图具有稀疏特性,建立每个超边的时间复杂度为O(mC2).由于C是指每个超边的前后C个近邻点,本文选择C为样本总数ns+nt的10%,因此C ≪(ns+nt).
以Melamine数据集为例,本文对上述两种超图构建方法的精度及耗时进行了对比分析,如图6所示.图中第1行是Melamine 数据集分别利用稀疏线性回归(lasso回归)和时间C近邻方法建立超图关联矩阵后的HD-PLSR 模型预测误差,记为lassoHD-PLSR 模型和C近邻HD-PLSR模型.第2行为利用时间C近邻方法建立超图所用的时间,记为T-C近邻HD-PLSR;第3行为利用稀疏线性回归构造超图所用的时间,记为T-lassoHD-PLSR.从图中可以看出,2种方法的预测误差结果相近.但是,lasso回归方法建立超图所用时间远远大于C近邻方法所用的时间,而且所耗的时间和样本个数成正比.因此本文选择C近邻方法代替稀疏约束,该方法不仅实现了稀疏约束保持局部近邻关系的作用,而且考虑了数据的时间序列结构特性,大大减小了运行时间.
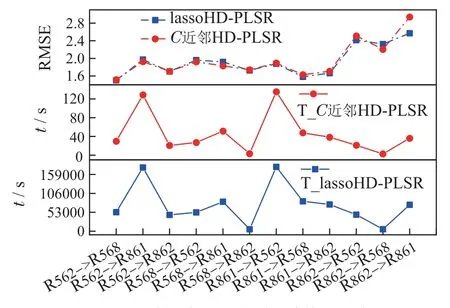
图6 Melamine数据集不同关联矩阵构造方法对比Fig.6 Comparison of different correlation matrix construction methods for melamine datasets
4.5 算法复杂度
本文算法的主要计算负担在于超图的构建和求解映射矩阵的步骤1-3.由第4.4节介绍可知,选时间C近邻构建超图的复杂度为O((ns+nt)mC2).步骤1和步骤2的时间复杂度为O(),步骤3的时间复杂度为.假设迭代次数为T1和T,则HDPLSR 模型的总时间复杂度可以表示为O(TT1(+)+(ns+nt)mC2),其中:T1是偏最小二乘框架中潜变量的个数d,T为求解映射矩阵的迭代次数.
4.6 参数分析
本文算法有3个重要的正则化参数,域适应正则化项的超参数γ、稀疏正则化项的超参数η、超图流形正则化项超参数σ.超参数对于不同的任务有不同的影响,设置搜索区间为{10-5,10-4,···,104,105},观察参数对模型预测精度的影响.
本文选择Melamine数据集的R568作为历史工况,R864作为当前工况;TE数据集的第1工况作为历史工况,第3工况作为当前工况;Corn数据集的m5作为历史工况,mp5作为当前工况对成分moisture预测,来进行参数寻优.首先分别固定潜变量的个数为d=10,5,2,超图流形正则化参数σ=0,验证域适应的正则化参数γ和η的影响,得到模型均方根误差随着γ在搜索区间内变化的结果,见图7(a).选择γ=1,再获得η在搜索区间内的均方根误差如图7(b),确定η=0.1,最后获得σ在搜索区间内的均方根误差,如图7(c).

图7 不同参数γ,η,σ下的均方根误差Fig.7 RMSE under different parameters γ,η,σ
观察图7发现,当正则化参数在较大的范围内变化时,本文模型具有相对鲁棒的性能.图7中γ对结果的影响较小,说明模型对该参数不敏感;η在3个数据集上的影响不同,说明了不同数据集受噪声影响的程度不同,但是可以获得公共的最优值0.1.引入超图正则化项后,预测结果的波动相对比较大,但是同样可以获得最小误差参数,而且观察到,超图流形正则化的引入使得模型的预测精度整体提升,再次说明了本文模型具有良好的泛化性.
5 结论
为解决工况变化引起数据分布差异所导致的传统软测量模型失准问题,本文提出了一种适用于回归的无监督域适应方法,即基于超图正则化的域适应多工况软测量建模方法.所提方法将基于特征表示的域适应方法嵌入在偏最小二乘回归模型的目标函数中,使所提取的公共潜变量空间不仅具有对历史工况标签的解释性,而且使历史工况和目标工况的潜变量具有相似的分布;同时,利用时间C近邻线性回归方法建立原始数据超图,作为目标函数的正则化项对潜变量求解过程进行约束,避免域适应过程破坏数据自身蕴含的相关关系,也大幅度的减小运行时间,满足工业实时性要求.使用3个典型多工况工业数据集对模型进行评估验证,结果表明本文所提出的HD-PLSR模型在跨工况条件下能有效发挥域适应功能,提高模型预测性能.但是,当当前工况样本点超过一定数量后,本文所提出的模型存在耗时较长的问题.下一步将研究在线递推的变工况软测量方法,使得算法耗时在可接受范围内,同时实现模型的在线更新.
